Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

2.3 Cyclic loading and fatigue 75

Figure 2.29: Stress concentration factors for a cylindrical shaft with a change of

section subjected to a bending moment M

radius r

Example 2. 7

A cylindrical shaft has a change of section from diameter 30 mm to diameter 25 mm

through a ﬁllet radius of 1.2 mm. The local bending moment is 200 Nm. Find the

maximum stress at the root of the ﬁllet.

The nominal bending stress is

nom

32 ×200 ×10

×25

= 130 MPa.

The ratios

= 1.2 ;

1.2

= 0.048

and hence interpolating on Figure 2.28, we have

= 1.98 .

The maximum tensile stress in the root is therefore

max

= 1.98 ×130 = 257.4 MPa.

76 2 Material Behaviour and Failure

Notch sensitivity

When stress concentrations are present, the heavily stressed region for which the fa-

tigue calculation is performed is very small. Following the discussion of §2.3.2, this

should be taken into account by using an appropriate value of C

, but in practice

the stress ﬁeld is so complex that it is difﬁcult to decide what value of V should be

used. Instead, a procedure has been developed based on direct experimental com-

parison between the fatigue strengths of specimens with and without certain stress

concentrations.

As we would expect from size effect considerations, theoretical estimates of fa-

tigue life become progressively more conservative as the characteristic length of the

stress concentration (e.g. the ﬁllet radius in Figure 2.29) gets smaller. We take this

into account by deﬁning a more realistic fatigue stress concentration factor K

the relation

= 1 + q(K

−1) , (2.90)

where q is an experimentally determined parameter known as the notch sensitivity

factor. Peterson suggests an approximate expression for q in the form

q =

1 +

a/r

, (2.91)

where r is the radius of the notch and a is a length scale deﬁned by the grain structure

of the material. Figure 2.30 gives values for the notch sensitivity of some low-alloy

steels, based on equation (2.91), with values of a taken from Figure 13.20 of Juvinall

(1967).

Notice that q is always less than unity, showing that the effect of a stress con-

centration in fatigue is always less than the theoretical effect (K

). Also, q falls

as the dimension r of the dominant feature is reduced, as we would expect from

size effect considerations. In principle, a perfectly sharp right angle corner (if such

a thing could be manufactured) would have an inﬁntely large K

, but the volume of

material so stressed would be zero, giving presumably a zero value of q. In practice,

the increased tendency to fatigue failure with increasing sharpness tends to level out,

albeit at too high a value for sharp corners to be desirable in design applications. One

advantageous consequence of this is that the inevitable microscopic scratches in the

surface of a component are less damaging to fatigue life than might be imagined.

Notice also that q depends very much on the material. An interesting point is

that cast iron has a very low notch sensitivity, so that geometric stress concentra-

tions have almost no effect on its fatigue behaviour. This is believed to be due to the

metallurgical structure of cast iron which is so inhomogeneous and permeated with

internal material defects that any additional geometric discontinuities have compar-

atively little effect.

2.3 Cyclic loading and fatigue 77

(mm)

0 0.04 0.08 0.12 0.16

r (in)

Figure 2.30: Notch sensitivity for some low-alloy steels

Example 2. 8

Figure 2.31 shows a bar with a change in section which is subjected to an alternating

bending moment M=M

cos(

t), where M

=1.2 Nm. The bar is machined from AISI

1010 steel for which S

=324 MPa.

Find the safety factor against fatigue failure using the values C

= 1 (i.e. 50%

reliability) and C

=0.9.

2 R

all dimensions in mm

Figure 2.31: Bar with a section change loaded in bending

78 2 Material Behaviour and Failure

For the theoretical stress concentration factor K

, we have D=12 mm, d =6 mm,

h =5 mm and r =2 mm in Figure C.4 of Appendix C, so

nom

6 ×12 ×10

5 ×6

= 40 MPa

and

= 2 ;

= 0.33 .

Interpolating in the ﬁgure, we estimate K

=1.38.

The notch sensitivity associated with a radius r = 2 mm for a steel of S

= 324

MPa is approximately q= 0.7, from Figure 2.30, so

= 1 + 0.7(0.38) = 1.266 .

Thus, the design stress is

= K

nom

= 1.266 ×40 = 50.6 MPa .

For the material strength, we estimate S

′

≈0.5 ×324 = 162 MPa and C

= 0.84

for a machined surface from Figure 2.27. Thus,

= 0.84 ×0.9 ×1.0 ×162 = 122 MPa

and the safety factor is

SF =

122

50.6

= 2.4 .

2.3.4 Effect of combined stresses

The discussion has so far been concerned with designing for a situation in which

the cyclic stress state consists of uniaxial tension/compression, as in the rotating

bending or push/pull tests. If a more complex cyclic stress system is present, we

need something akin to a failure theory to reduce it to an equivalent tensile stress

which can be compared with S

. Fortunately it is found that the von Mises deviatoric

strain energy theory correlates quite well with the results of biaxial fatigue tests and

hence design can be based on the equivalent tensile stress as deﬁned by equation

(2.54).

2.3.5 Effect of a superposed mean stress

In many engineering applications, the stresses do not ﬂuctuate between equal positive

and negative values — there is also a superposed constant mean stress. A typical

example is the rotating shaft of Figure 2.32, which experiences cyclic loading due to

bending (as in the rotating bending test), but also transmits a torque T , leading to a

constant torsional shear stress.

2.3 Cyclic loading and fatigue 79

Figure 2.32: Rotating shaft subjected to bending and torsion

The stress state in such cases can be characterized in either of two ways. We can

specify the maximum and minimum stresses (

max

min

), or the mean and alternat-

ing stresses (

). Which is more appropriate depends on the application. In the

example of Figure 2.32, the mean stress is caused by the torque and the alternating

stress by the bending moment, so it is natural to choose this method of description,

for which

sin(

t) , (2.92)

where

is the rotational speed of the shaft.

However, a chair experiences one state of stress when you are sitting on it (pre-

sumably

max

) and another (

min

) when you are not, so these quantities will be the

natural starting point for the calculation. It is easy to convert from one description to

the other using the relations

max

min

;

max

−

min

(2.93)

and

max

;

min

−

. (2.94)

A special case that occurs quite frequently is that where the minimum stress state is

one in which the component is unloaded (

min

=0), in which case

max

/2.

We recall from §2.2.4 that cracks can transmit compressive tractions by crack

face contact, but are opened by tensile stresses. Thus, we should anticipate that the

superposition of a tensile mean stress will encourage fatigue failure, whilst a com-

pressive mean stress will tend to inhibit it. Experimental results conﬁrm this be-

haviour. Results are usually presented as a plot of

against

at the fatigue limit

— i.e. as a failure surface in

space. Results for a typical steel are shown in

Figure 2.33. Points under the solid curve correspond to stress states that will not

cause fatigue failure, regardless of the number of cycles of loading. Notice that two

points on this curve can be located immediately from our previous discussion. If the

mean stress

= 0, the loading is completely reversed and the fatigue limit is de-

ﬁned by

as deﬁned in §2.3.1. This corresponds to point A on Figure 2.33. On

the other hand, if

= 0, there is no alternating stress and failure will occur when

80 2 Material Behaviour and Failure

the mean stress reaches the ultimate tensile strength of the material (

= S

). This

corresponds to point B in Figure 2.33.

Goodman line

tension

compression

A(S )

B(S )

Figure 2.33: Fatigue limit under combined mean and alternating stress

Experimental curves such as Figure 2.33 are generally found to be convex up-

wards, so a conservative failure surface can be deﬁned by locating the limiting points

A,B and joining them by a straight line. This line is known as the Goodman line and

the corresponding diagram as the Goodman diagram. If the mean stress is compres-

sive (

< 0), the fatigue limit is generally increased, but it is usual to make the

conservative approximation of neglecting this effect — i.e. to treat the failure sur-

face as horizontal in the range

< 0. These approximations are represented by the

dotted straight lines in Figure 2.33. They are quite conservative and various methods

have been proposed for making more accurate approximations to the experimental

data.

Example 2. 9

The critical point in an engineering component experiences a tensile stress that ﬂuc-

tuates between the maximum and minimum values

max

= 140 MPa,

min

= 80 MPa.

The material has an ultimate strength S

= 560 MPa and an endurance limit (after

taking account of surface and gradient factors) S

=180 MPa. Estimate the factor of

safety against fatigue failure.

We ﬁrst note that

140 + 80

= 110 MPa ;

140 −80

= 30 MPa .

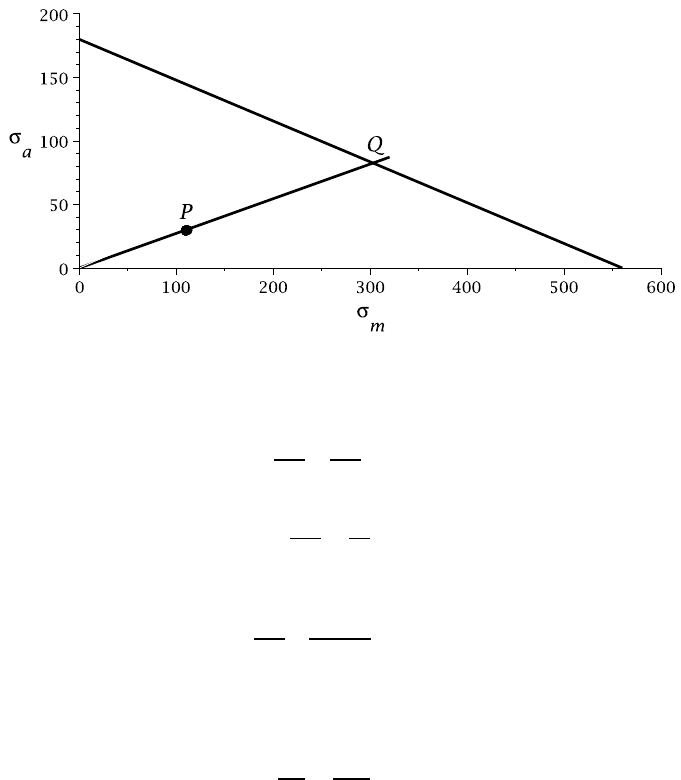
The Goodman diagram has the form shown in Figure 2.34 and the operating point

is at P(110,30). It is clearly on the safe side of the Goodman line and the safety factor

SF =

which can be estimated graphically to acceptable accuracy as

SF = 2.8 .

See for example Shigley and Mitchell (1983), §7.14.

2.3 Cyclic loading and fatigue 81

(MPa)

Figure 2.34: Goodman diagram for Example 2.9.

Alternatively, we can argue that the Goodman line is described by the equation

180

560

= 1

and the load line OPQ by

110

Both equations are satisﬁed at Q, so eliminating

, we obtain

180

3 ×560

= 1 ,

with solution

=82.6 MPa.

The safety factor then follows from

SF =

82.6

= 2.75 .

However, we should emphasise that the accuracy of design calculations doesn’t gen-

erally warrant such sophistication. The visual estimate from the sketch is as good as

we are likely to need.

Effect of contained plasticity

For ductile materials, the yield strength S

is signiﬁcantly lower than the ultimate

strength S

and hence there are regions in the lower right-hand corner of the Good-

man diagram where static yield will occur during the ﬁrst application of the load. If

82 2 Material Behaviour and Failure

in a design calculation we obtain high mean stresses in this range, their signiﬁcance

depends on whether or not a stress concentration is present.

If there is no stress concentration (for example, if the mean stress results from a

constant torque or axial force on a uniform bar), extensive plastic deformation will

occur, with strains that are an order of magnitude larger than those occurring during

elastic deformation. The material will become work hardened — i.e. it will develop a

higher yield stress in response to the high strains and this is why it can support max-

imum stresses in excess of those causing yield in a virgin material. Notice however

that we would be unlikely to operate in this range because the plastic strains might

compromise the performance of the component.

If the component contains a stress concentration and if the design calculations

show a mean stress exceeding the yield stress after the stress concentration factor

has been included, the predictions are misleading. When the loads are ﬁrst applied,

there will come a point when yield will occur locally near the stress concentration.

Up to this point, the stresses are correctly given by the elastic calculation, but as the

load is increased further, the stress in the stress concentration levels off at the yield

stress S

. In order to produce a local stress in excess of S

— i.e. to produce signiﬁ-

cant work hardening — we would need to have large plastic strains and these cannot

occur in a local region at a stress concentration, since the strains are dominated by

the elastic behaviour of the surrounding material.

time

(a) (b)

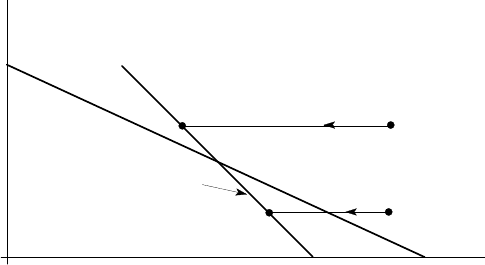
Figure 2.35: Effect of contained plasticity at a stress concentration: (a) Theoretical

stress history exceeding the yield stress, (b) Actual stress history taking into account

local yielding

Now suppose that a component with a stress concentration is loaded so as to

produce the maximum theoretical elastic tensile stresses shown in Figure 2.35 (a). In

practice, yielding will start at A and continue as long as the applied loads increase

— i.e. to point B. The stress will remain at S

during this yielding process, but after

point B, unloading will occur elastically, so that the actual stress history will be as

shown in Figure 2.35 (b). In particular, we notice that the stress history is modiﬁed

by yield in such a way that the alternating stress

remains unchanged, but the mean

stress is reduced so as to reduce

max

to S

2.3 Cyclic loading and fatigue 83

We then have

max

≡

and hence

= S

−

. (2.95)

This equation corresponds to the line CD on the Goodman diagram of Figure 2.36.

If the calculated point on the Goodman diagram lies to the right of CD, local yield-

ing will reduce

until the effective operating point lies on CD. For example, the

calculated point P

is moved to P

∗

, which is below AB and therefore safe, whilst P

is moved to P

∗

, which is above AB and therefore unsafe.

We conclude that if the calculated mean stress

, fatigue failure will occur

if and only if

≥S

, where S

are the coordinates of the point D.

D(S , S )

Figure 2.36: Interpretation of local yielding on the Goodman diagram

2.3.6 Summary of the design process

As we have seen, many factors are involved in fatigue failure and the design process

can get quite complicated. We therefore give a concise summary of the steps as

follows:-

(i) Material properties

(a) Estimate S

either from tabulated values or by experiment.

(b) Estimate S

′

, either directly from tabulated experimental data or by using

equations (2.73–2.75).

(§2.3.2 above) and hence obtain the design fatigue limit

= S

′

(d) Sketch the Goodman diagram.

(e) Find the notch sensitivity factor from Figure 2.30,

(ii) The nominal loading may involve (i) bending, (ii) torsion, (iii) axial force, (iv)

shear force, each of which may have mean and alternating components. Separate

the loading into these components (e.g. mean torque, alternating torque, mean

axial force etc.).

84 2 Material Behaviour and Failure

(iii) For each loading component,

(a) calculate the nominal stresses,

(b) ﬁnd K

by interpolation in the appropriate ﬁgure in Appendix C or other

reference works,

=1 + q(K

−1),

(d) calculate the actual stress

nom

(iv) Take all the stresses resulting from alternating loads and combine them to obtain

an alternating equivalent tensile stress

using equation (2.54) or (2.55, 2.56).

Repeat using the mean stress components to ﬁnd the mean equivalent tensile

stress

(v) Plot the operating point P(

) on the Goodman diagram. The design is

safe if P lies under the Goodman line and the safety factor can be estimated by

determining the ratio between the distances from the origin to P and the distance

along the same line to the failure surface.

(vi) If

in Figure 2.36, the safety factor is given by S

Example 2. 10

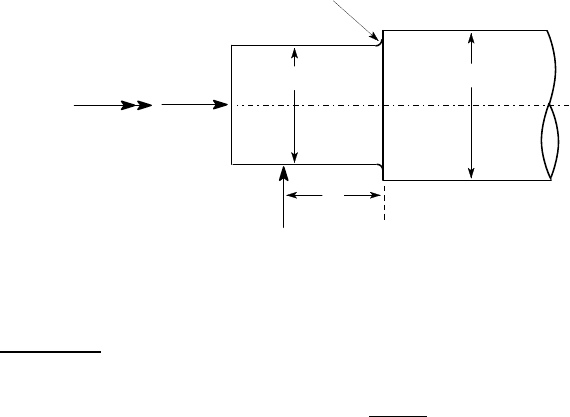
Figure 2.37 shows part of the shaft for a concrete mixer that is subjected to a com-

pressive axial force of 40 kN, a transverse bearing force of 50 kN and a torque of 2

kNm. The material of the shaft is 1018A carbon steel with S

= 341 MPa, S

= 220

MPa and it has a machined ﬁnish. Estimate the safety factor against fatigue failure,

based on a reliability of 50%.

2 R

φ135

φ115

40 kN

2 kNm

50 kN

all dimensions in mm

Figure 2.37: Concrete mixer shaft. Notice the commonly used notation

115 for a

shaft of diameter 115 mm and 2 R for a ﬁllet radius of 2 mm.

Note that since the principal effect of a mean stress is to hold the cracks open during fatigue,

there is some justiﬁcation for using the maximum principal stress

in place of the von Mises equivalent stress, particularly when the stresses are predominantly

compressive.