Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

2.3 Cyclic loading and fatigue 65

set of conditions of manageable proportions, which can be tested and the results

tabulated.

The most basic fatigue test is one in which a specimen is subjected to cyclic

tension and compression, such that the axial force F varies according to the equation

F = F

sin(

t) , (2.72)

where t is time. For obvious reasons, this is referred to as completely reversed load-

ing.

In practice, it is a great deal easier to achieve this stress history by loading the

specimen in bending and then rotating it, so that a given portion of the specimen near

the surface passes through the zones of maximum tensile and maximum compressive

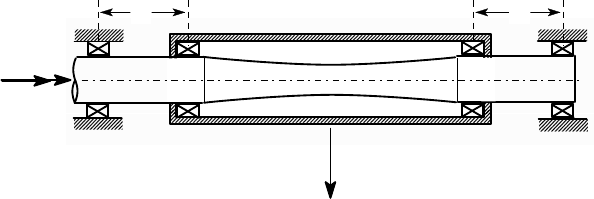
stress once per revolution. A typical experimental system is shown schematically in

Figure 2.24. A force F is applied to the carrier ABCD, causing a constant bending

moment M = Fd/2 in the central section of the specimen.

Notice how the specimen is gently rounded to a minimum diameter, so as to

ensure that the failure occurs in a region where the nominal stresses are well-deﬁned,

rather than at a change of section or other stress concentration. We shall see below

that fatigue strength is signiﬁcantly inﬂuenced by the size of the specimen, so a

standard specimen of 0.3 inch (7.6 mm) diameter is generally used.

Figure 2.24: Rotating bending test for fatigue failure

The test procedure is to apply a load below that required to produce immediate

static yield, set the machine rotating and count the number of rotations until failure

occurs. The results are then plotted on an ‘S–N curve’, which shows the stress level

S as a function of the number of cycles to failure N. Curves for a typical steel and

aluminium alloy are shown in Figure 2.25. A logarithmic scale is generally used,

since the lives of different specimens can vary by several orders of magnitude. It is

not practical to conduct tests for much more than 10

cycles, because they are very

time consuming. Even so, for these long running tests, the test machine has to be left

running continuously for several days and therefore has to be instrumented to detect

failure and switch itself off.

66 2 Material Behaviour and Failure

100

200

400

280

140

aluminium alloy

steel

(MPa)

Figure 2.25: S–N curves for a typical steel and an aluminium alloy

For steels, the fatigue strength decays with number of cycles up to about N =10

cycles, after which the curve levels off. There is therefore a fatigue limit denoted

by S

(also called the endurance limit), below which it seems

that failure will not

occur, no matter how long the test is run. This is a very useful result in design, since

it means that we do not have to design for a speciﬁc number of cycles of loading if

that number is greater than 10

To get some idea of the number of cycles accumulated in some typical compo-

nents during a normal service life, consider the following examples. At the upper

extreme, an engine crankshaft running 24 hours a day at 5000 rpm for 10 years will

accumulate

N = 5000 rpm ×60 min/hr ×24 hr/day ×365 days/year×10 years

= 26 ×10

cycles.

This is about the largest value of N you are likely to encounter in rotating machinery,

since most machines don’t run all the time and 5000 rpm is quite a high speed.

Larger numbers of cycles can be accumulated in devices subjected to high frequency

vibration. A machine running at 200 rpm for 2 hours a day and 5 days per week

would accumulate

N =200 rpm×60 min/hr×2 hr/day×5 days/week×52 weeks/year×10 years

= 62 ×10

cycles.

However, there are some applications involving much smaller numbers of cycles.

For example, every time a machine is started, it ‘warms up’, and there will be thermal

stresses associated with the differential thermal expansion of the parts. These stresses

may be constant during operation, so one complete reversal occurs only every start

We qualify this statement because no-one knows what would happen in such cases if the

number of cycles were several orders of magnitude greater than those reached in tests or

service conditions.

2.3 Cyclic loading and fatigue 67

up, which may be once or twice a day. Fatigue under these conditions is referred to

as low cycle fatigue (for obvious reasons) and in such applications a more efﬁcient

design can be obtained by making use of the sloping portion of the S–N curve. The

Comet disasters referred to above were eventually attributed to fatigue associated

with cabin pressurization, which typically cycles only once per take off and landing.

However, the above examples show that in many applications, N is large enough to

justify using the fatigue limit only.

The concept of a fatigue limit is so useful that we invent one even when it is

not discovered experimentally. Thus, with aluminium and its alloys, the S–N curves

continue to fall with N throughout the range, although there is a levelling trend as

shown in Figure 2.25. Under these conditions, we typically design to a fatigue limit

equal to the stress level S for a life of 10

or 10

cycles. In other words, we

approximate the experimental curve by a horizontal straight line in the practical range

of N.

Estimates for the fa tigue limit

Ideally, we should use values for S

for the same material as in the component being

designed. However, in practice there are so many different alloys, with a correspond-

ing number of different heat treatments and production methods (all of which affect

the fatigue strength) that we are often unable to obtain appropriate data. More signif-

icantly, the exact choice of material and heat treatment will often not be made until

a fairly late stage in the design process, so it is useful to have a rough idea of what

values of S

to expect for a range of common materials.

A good rule of thumb is that the fatigue limit for a polished specimen will be

between a quarter and a half of the ultimate tensile strength for the same material. The

ultimate strength S

is the stress required to cause rupture of a tensile test specimen.

It can be signiﬁcantly greater than the stress at ﬁrst yield S

, due to the phenomenon

of work hardening. There is much more data available for tensile strength than for

fatigue limit and in the worst case we can always ﬁnd S

by testing a specimen

ourselves — it is much easier to perform a single monotonic tensile test than to

conduct a series of fatigue tests.

For steels, Juvinall (1983) §8.3 suggests the relation

′

≈ 0.5S

≈0.25 × BHN (in ksi) ≈1.73 × BHN (in MPa), (2.73)

where BHN is the hardness value obtained in the Brinell hardness test and the prime

(

′

) in S

′

is used to indicate that this is the value obtained in a rotating bending test on

a standard polished specimen. Note however that S

′

for extremely hard steels levels

off at a value of about 100 ksi (700 MPa) and this value should be used if equation

(2.73) predicts a larger value.

A corresponding result for aluminium alloys is

′

≈ 0.4S

if S

< 48 ksi (330 MPa) (2.74)

≈ 19 ksi (130 MPa) if S

> 48 ksi (330 MPa). (2.75)

68 2 Material Behaviour and Failure

However, it should be emphasised that these results are only very approximate. They

may be used in the spirit of §1.2.2 to obtain estimates of the fatigue strength of

a component, but there is no substitute for a fatigue test on the actual material in

applications where large safety factors cannot be used.

2.3.2 Statistics and the size effect

The stress concentration due to a fatigue crack increases with its length, so the crack

grows more rapidly during the later stages of the process. Indeed, by the time the

crack is big enough to be detected, the fatigue life of the component is usually almost

exhausted. You can test this crudely by subjecting a piece of wire to half the number

of loading cycles needed to cause failure and then looking (probably unsuccessfully)

for signs of cracking.

The greater part of the fatigue life is therefore associated with initiation and

development of cracks on the microscopic scale. Cracks are believed to start from

pre-existing defects in the material or the component and it is a matter of luck (or

to be more scientiﬁc, of statistics) whether a suitably-oriented defect exists in the

most heavily stressed region. This has the unfortunate effect of making the process

of designing against fatigue very dependent on the exact condition of the material

and on minor details of the geometry. Most of these effects can only be assessed

experimentally, so we tend to allow for them by ‘correction factors’ multiplying the

fatigue limit. Such factors will be denoted by the symbol C with appropriate sufﬁces.

It also follows that fatigue data is subject to considerable statistical scatter and, of

two otherwise identical specimens, one may fail at a signiﬁcantly lower stress (or

smaller number of cycles) than the other. In this section we shall examine some of

these questions using the simplest appropriate statistical hypothesis. For a more so-

phisticated approach to the question of statistical design against fatigue, the reader is

referred to Collins (1981).

The Weibull distribution

Suppose that a given volume of material V is subjected to uniform alternating tensile

stress S and contains a random distribution of microdefects of various dimensions

and orientations. Fatigue failure will eventually occur if at least one of these defects

weakens the material sufﬁciently for crack initiation to occur at stress S.

The probability of ﬁnding a suitably oriented defect clearly increases if the vol-

ume V increases. Suppose we deﬁne R(S,V ) as the reliability — i.e. the probability

that a specimen of volume V survives (i.e. does not fail in fatigue) either indeﬁnitely

or for a given number of cycles under an alternating stress S. The probability of

failure P(S,V ) of the same specimen will then be

P(S,V ) = 1 −R(S,V) . (2.76)

If we now test a specimen of volume nV , it is essentially the same as if we were to test

n specimens each of volume V simultaneously and count the system as having failed

2.3 Cyclic loading and fatigue 69

if any one of the n were to fail. The probability of survival in this case is [R(S,V )]

and we therefore conclude that

R(S,nV) = [R(S,V )]

. (2.77)

The simplest statistical distribution that satisﬁes

this condition is the two-

parameter Weibull distribution

, deﬁned by

R(S,V ) = exp

−









, (2.78)

where V

is a reference volume (e.g. the volume of stressed material in the standard

0.3 in diameter rotating bending test) and S

is the alternating stress at which the

reliability of the reference volume is R(S

)= exp(−1)=0.368.

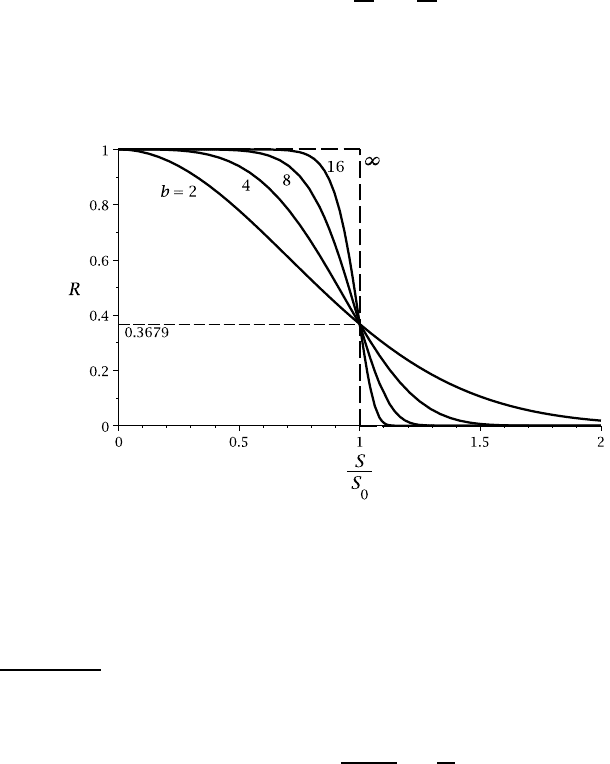
Figure 2.26: Effect of b on the cumulative Weibull distribution

The parameter b in equation (2.78) determines the degree of scatter or variabil-

ity in the distribution. Figure 2.26 shows the reliability as a function of normalized

alternating stress S/S

for V =V

and various values of b. At very large b, the curve

approaches the Heaviside step function H(− S/S

), corresponding to a material of

The reader can verify by substitution that the deﬁnition (2.78) satisﬁes the condition (2.77).

There is also a three-parameter Weibull distribution deﬁned through the equation

R(S,V ) = exp

−



S −S

−S







where S

is an additional parameter that can be used to improve the ﬁt of the distribution

to the statistical data.

70 2 Material Behaviour and Failure

which all specimens will exhibit a fatigue strength exactly equal to S

. As b is re-

duced, the variability in specimen strengths increases. For example, at b = 50 the

standard deviation in the strengths is about 2.5% of S

, whereas at b = 10 it is about

11%.

In an ideal world, we would have statistical information on the distribution of

fatigue strengths for all the materials we might wish to use, but this would be a

very large amount of experimental data. In practice, sufﬁciently accurate estimates

of fatigue strength can be made using representative values of b for broad classes

of materials. For example, experimental data for steels and other common structural

metals suggest that an appropriate standard deviation for the distribution is about 7%

of the mean strength at any given life corresponding to a Weibull modulus b ≈16.

We shall therefore adopt this value in subsequent examples. More accurate data for

the Weibull modulus for various materials can be found in the reference works at the

end of this chapter.

Reliability

Equation (2.78) essentially deﬁnes S

as the alternating stress at which a specimen of

volume V

has a reliability of 0.368 (36.8%). Generally we shall wish to design for a

higher value of reliability such as 90% or 99%. We ﬁrst note that standard data from

the rotating bending test usually report median values of the fatigue limit — i.e., S

′

is the alternating stress at which the survival rate is 50%.

Under these conditions,

R(S

′

) = exp

−



′



= 0.5 (2.79)

and hence

= S

′

[−ln(0.5)]

1/b

. (2.80)

Suppose now that we want to design to a reliability of 99% — i.e., we wish to

choose S such that R(S,V

)= 0.99. We have

R(S,V

) = exp

−





= 0.99 (2.81)

and hence

S = S

[−ln(0.99)]

−1/b

= S

′



ln(0.99)

ln(0.5)



1/b

= 0.77S

′

, (2.82)

using b = 16. More generally, for a reliability R, we design to a strength

S = C

′

, (2.83)

where C

is a reliability factor deﬁned by



ln(R)

ln(0.5)



1/b

. (2.84)

2.3 Cyclic loading and fatigue 71

The size effect

Equation (2.78) also shows that two components will have the same reliability if

they have the same value of S

V , where V is the volume of material subjected to the

maximum level of alternating stress. Thus to achieve 50% reliability in a specimen

of stressed volume V , we must design to a strength

S = C

′

, (2.85)

where the size factor or gradient factor C

is deﬁned by





1/b

. (2.86)

The name of the gradient factor derives from the fact that the size of the stressed

region depends upon the rate at which the stress falls with distance from the point of

maximum stress (usually at the surface). In particular, note that in a reversed axial

loading (push-pull) test, all the specimen experiences the maximum stress cycle,

whereas in a rotating bending test, only regions near to the surface experience it.

To get an idea of the magnitude of C

, notice that if V /V

= 10 (i.e. if the stressed

volume is ten times greater than that in the standard specimen), C

=0.87.

Similar calculations can be performed for components of other sizes, but since

the fatigue limit is not very sensitive to size (in the above calculation changing the

size by a factor of 10 only reduced the strength by 13%), it is sufﬁcient to use a

rough estimate for C

. A good rule of thumb is to reduce C

by 0.1 for each order

of magnitude that the stressed volume exceeds that in the standard specimen. Also,

if the component is comparable in size to the standard specimen but is loaded in

reversed tension rather than in bending, use C

=0.9 on the grounds that only about

10% of the specimen is at the highest stress level in the bending test.

Surface ﬁnish

It is well known that components with rough surfaces are more prone to fatigue

failure than those which are polished. It is tempting to explain this by saying that

rough surfaces are rough simply because they contain microcracks which act as ini-

tial defects from which fatigue cracks develop. However, more rigorous investiga-

tions show that the kind of surfaces which are most prone to fatigue failure (such

as rough machined surfaces) have other properties which may be more important in

fatigue than the roughness. They typically have a surface layer of heavily worked

material where the ductility is nearly exhausted and hence where cyclic loading will

produce failure earlier than in virgin material. Also in many cases the heat gener-

ated during the machining process causes yielding in the surface layers which leaves

residual tensile stresses. Tensile residual stresses are undesirable, since if any mi-

crocracks exist normal to the surface, they will tend to open. We saw in §2.2.4 that

crack propagation is inhibited when the loading tends to close the crack and hence

72 2 Material Behaviour and Failure

any pre-existing stress tending to hold cracks open will increase the probability of

propagation.

Hardness (H

)

120 200 280 360 440 520

(ksi)

0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8

(GPa)

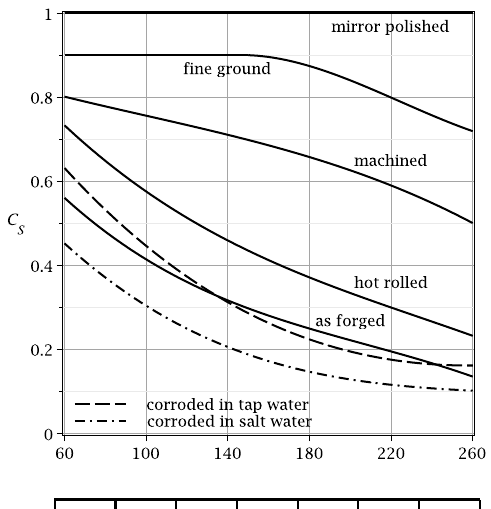
Figure 2.27: Effect of surface condition on fatigue limit for steels with various man-

ufacturing methods and hardnesses. Adapted from R.C.Juvinall, Fundamentals of

Machine Component Design, John Wiley, New York,

1983 by permission of John

Wiley & Sons, Inc.

These factors are almost impossible to quantify with any degree of conﬁdence,

so we tend to present data in terms of the measurable surface roughness and the

method of manufacture. For example, typical values for steels are shown in Figure

2.27. Notice that the effect of the ﬁnishing technique on fatigue limit depends on

the hardness of the material — the stronger steels generally have lower ductility and

therefore are more sensitive to surface condition. This means that if we try to increase

fatigue strength by using a stronger steel, there is a law of diminishing returns. Also,

if we want to make full use of the stronger steel, we have to pay the price of making

the part with a more expensive ﬁnishing operation such as grinding or polishing.

Notice also that it is particularly important to ensure that this high quality ﬁnish is

retained through any stress concentrations at section changes or notches and this can

be quite hard to achieve.

2.3 Cyclic loading and fatigue 73

Figure 2.27 is plotted in terms of a surface factor C

, which acts to reduce the

effective fatigue limit of the material. The standard rotating bending specimens are

mirror polished, because this reduces the scatter in the experimental results, and they

therefore have by deﬁnition a surface factor of unity.

Summary

All of the above factors act together to modify the fatigue limit of a material. In

design, we therefore use the value

= S

′

, (2.87)

where S

′

is the fatigue limit obtained in the standard rotating bending test.

Example 2. 6

Figure 2.28 shows an automotive engine connecting rod which is forged from AISI

1040 steel, for which S

=570 MPa. Determine an appropriate design value for S

a reliability of 99.9% is required.

120

all dimensions in mm

Figure 2.28: Automotive engine connecting rod

We ﬁrst estimate S

′

from equation (2.73) as

′

= 0.5 ×570 = 285 MPa .

The connecting rod is forged, so an appropriate surface factor is obtained from Figure

2.27 as C

=0.45.

The reliability factor



ln(0.999)

ln(0.5)



1/16

= 0.665 .

Finally, we need to estimate a size factor C

. For this purpose it is sufﬁcient to note

that the linear dimensions of the connecting rod are about three times larger than

those of the standard specimen, so V ≈27V

, giving

section A-A

74 2 Material Behaviour and Failure





1/16

= 0.81 .

Hence, an appropriate design value for S

= 0.45 ×0.665 ×0.81 ×285 = 69 MPa .

Notice that a substantial improvement in fatigue strength could be achieved in this

case by machining the surfaces of the connecting rod.

2.3.3 Factors inﬂuencing the design stress

Real engineering components will generally be a great deal more complex than the

standard rotating bending fatigue specimen and they will also be subjected to more

complex loading. In such cases, we need to calculate a design stress which can be

compared with the results of the standardized tests discussed above.

Stress concentrations

Engineering components typically contain geometric features such as changes of

section, holes or notches that cause local stress concentrations. As with the crack

shown in Figure 2.13, the idea of the ﬂow of load through the structure can often be

used to predict which features are likely to lead to high stresses, but the calculation

of the theoretical stress ﬁeld is difﬁcult and usually requires a numerical solution.

However, results for a wide range of geometries are tabulated in the literature.

The results are presented in the form of a dimensionless multiplier on the nominal

stress

nom

, which is usually the stress which would be obtained from elementary

mechanics of materials theory if the stress concentration were ignored. Thus, the

actual stress

is given by

= K

nom

, (2.88)

where K

is the theoretical stress concentration factor. In reference works, the math-

ematical expression for

nom

will be given explicitly either in the ﬁgure or in the

accompanying text.

Figure 2.29 shows stress concentration factors for bending of a cylindrical shaft

with a change in section from diameter D to d through a ﬁllet radius r. The nominal

stress is here based on the elementary theory using the smaller diameter d and is

therefore

nom

32M

, (2.89)

where M is the bending moment.

Stress concentration charts for some other common geometries and loadings are

given in Appendix C.

See for example Peterson, (1974), Pilkey, (1994).