Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

2.1 Transformation of stresses 35

(2.25)

(2.26)

, (2.27)

which could also be deduced directly by noting that equation (2.16) must be capable

of factorization in the form

(

−

)(

−

)(

−

) = 0 . (2.28)

The importance of stress invariants stems from the fact that the failure of an

isotropic material cannot depend upon the orientation of the stress ﬁeld and hence

must depend on a stress measure that is invariant under coordinate transformation.

This question is discussed in §2.2 below.

Cases where one principal direction is known

The largest stresses in engineering components almost always occur at the surface,

rather than at interior points. For example, in bending, the tensile stress is linearly

proportional to the distance from the neutral axis and hence the maximum stress

occurs at the greatest distance from this axis, which must necessarily be adjacent to

an exposed surface. Most exposed surfaces are traction-free, so if we choose a local

coordinate system such that the z-direction is the outward normal from the surface,

the components

= 0. In some cases, there may be a non-zero normal

traction at the surface (i.e.

6=0) due to contact with another body or pressure of a

gas, but it is really quite difﬁcult to apply shear tractions to an exposed surface.

If the shear stresses

are zero at the point of interest, it follows imme-

diately that the z-direction is one of the principal directions and the other two must

therefore lie in the orthogonal x, y plane. These directions and the corresponding

principal stresses can then be found from the two-dimensional analysis of §2.1.1,

since, although there may now be non-zero tractions

on the triangular faces of

the three-dimensional element equivalent to Figure 2.1 (b), the corresponding forces

will not enter into the in-plane equilibrium equations (2.1, 2.2).

Thus, although there are strictly no two-dimensional problems (all bodies are

three-dimensional), most of the stress transformation questions that arise in design

reduce to an application of the two-dimensional equations of §2.1.1.

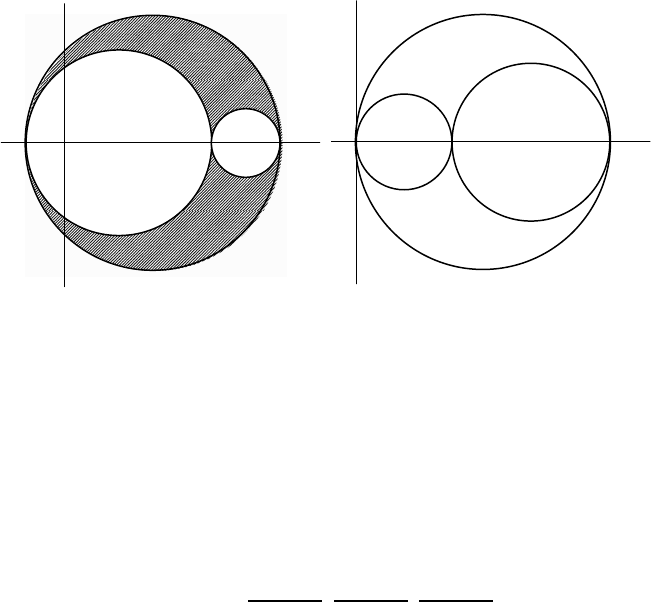
Three-dimensional Mohr’s circles

Once we have determined the three principal stresses

, we can use a Mohr’s

circle to ﬁnd the stress components on any plane that can be reached by rotating any

of the principal planes about one of the principal coordinate axes. Three such circles

can be drawn, as shown in Figure 2.5 (a).

Tangential tractions may result from frictional contact or from viscous drag of a ﬂuid, but

the resulting tractions are generally small compared with failure strengths for the material.

36 2 Material Behaviour and Failure

(a) (b)

Figure 2.5: Three dimensional Mohr’s circles: (a) the general case, (b) the case

where

=0 and

>0.

Of course, there exist a whole range of planes that cannot be reached by such a

rotation, but it can be shown that the normal and shear stresses on all these planes

correspond to points in the area bounded by the three circles and shown shaded

in Figure 2.5 (a) (Boresi et al. (1993), pp.48–51). The maximum tensile stress is

therefore the largest of

and the maximum shear stress is the largest of the

three radii — i.e.

max

= max(

) (2.29)

max

= max



−



. (2.30)

It is important to realize that all real world problems are three-dimensional, even

if the three stress components

are zero (and hence one of the three prin-

cipal stresses is zero). Suppose we analyze a system and determine that both the

non-zero principal stresses

are tensile (positive) — for example

>0. A

na¨ıve analysis, neglecting the three-dimensionality of the problem would identify the

maximum shear stress as (

−

)/2, whereas it is clear from the three-dimensional

Mohr’s circles of Figure 2.5 (b) (using

=0) that it is

/2.

2.2 Failure theories for isotropic ma terials

If we take a block of material and machine a test specimen from it, the behaviour of

the specimen (e.g. the tensile strength or the elastic properties) might depend on the

orientation of the specimen relative to the original block. Such a material is referred

to as anisotropic — i.e. it does not have the same properties in all directions. A

simple example of anisotropy is a ﬁbre-reinforced composite in which all the ﬁbres

are parallel. In this case, a tensile specimen cut with the ﬁbres along the test axis will

generally be stronger and stiffer than one cut across the ﬁbre axis. Other sources of

anisotropy include the orientation of rows of atoms in a single crystal.

2.2 Failure theories for isotropic materials 37

For most design calculations (with the important exception of ﬁbre-reinforced

composites and wood), we make the simplifying assumption that the material is

isotropic, meaning that it has the same properties in all directions and hence that

all test specimens will have the same properties regardless of orientation. In many

cases, the material may be quite inhomogeneous and anisotropic on the microscopic

scale. For example, it may have a granular structure and each grain may have its

atoms aligned in different directions. Also there may be distributions of impurities,

microcracks and voids. However, if these irregularities are sufﬁciently small in size

and are randomly oriented and distributed, a larger specimen of the material will

appear isotropic.

Local failure of an isotropic material must depend only on measures of the sever-

ity of the local stress state without reference to direction, and hence must be capable

of description in terms of quantities that are invariant under coordinate transforma-

tion. These quantities include the set of three principal stresses

or the three

stress invariants I

of equations (2.17–2.19). Any one of these sets can be deter-

mined from the other, so a comprehensive set of failure tests for an isotropic material

involves the variation of only three parameters.

2.2.1 The failure surface

Suppose we could devise a machine that is capable of applying arbitrarily chosen

values of the three principal stresses

to a suitable test specimen of a given

material. Testing would involve varying one or more of the stresses until failure oc-

curs.

Failure under plane stress

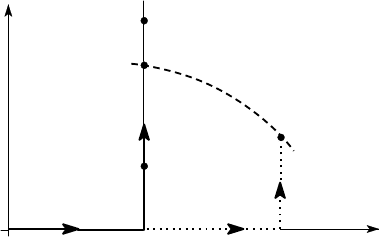
Consider ﬁrst the simple case of plane stress, where one of the three principal

stresses,

is always zero. Possible stress states can then be presented as points

on a graph with coordinates (

) and loading scenarios will be directional lines

on this plot as shown in Figure 2.6.

Figure 2.6: Plane stress loading scenarios leading to failure

38 2 Material Behaviour and Failure

For example, the line OA

describes a test in which all three stresses are origi-

nally zero;

is then increased slowly until it reaches the value OA

, after which it is

held constant whilst

is increased, until failure occurs at B

. A second test could be

performed using a similar scenario, but with a different value OA

for

, in which

case the critical value of

) would also generally be different, as shown.

If we connect the failure points B

etc. in Figure 2.6 by a line, this line will

deﬁne a boundary separating safe states of stress from unsafe states. Thus, the point

is safe because it is passed without failure during the test OA

, but the point C

is unsafe, because failure occurs at B

before C

is reached.

Failure can occur in compression as well as tension, so the complete failure en-

velope is likely to be a closed curve as shown in Figure 2.7. Everywhere inside the

curve, including the origin, where all three stresses are zero, is safe, but failure will

occur if we try to cross the failure envelope into the surrounding unsafe region.

safe

unsafe

Figure 2.7: Failure envelope for plane stress

It is important to recognize that this argument depends on the assumption that

failure is determined by the instantaneous state of stress and is not inﬂuenced by the

history of the loading before the failure point. For most materials, this is a reasonable

assumption if the deformation inside the failure envelope is elastic and the loading

scenario does not involve stress reversal — for example, failure will occur at the

point B in Figure 2.7 for any of the ‘monotonic’

loading scenarios 1,2,3. However,

scenario 4, involving a number of cycles of loading and unloading within the safe

region, is likely to lead to failure before the monotonic failure envelope is reached.

We shall refer to a loading scenario as monotonic if the none of the six stress rates

change sign during the process, where

≡

∂σ

∂

t and t is time.

2.2 Failure theories for isotropic materials 39

This process is known as fatigue and will be discussed in more detail in §2.3 be-

low. For the rest of this section, we shall restrict attention to failure under monotonic

The three-dimensional failure envelope

The ideas of the previous section are easily extended to the case where all three

principal stresses can be non-zero. For this purpose, we need to imagine a three-

dimensional graph in which

deﬁne the three axes. Loading scenarios will

again correspond to lines in this three-dimensional space and failure points can be

joined to deﬁne a closed surface such that all points inside the surface correspond to

safe states of stress and all points outside the surface are unsafe.

2.2.2 The shape of the failure envelope

So far we have discussed ways of presenting data about the failure of materials under

general states of stress, but we have not given any indication of the form the failure

criterion is likely to take. In other words, what shape would we expect the failure

envelope to have? Many authors have proposed theories of how materials might be

expected to behave, but ultimately the question can only be answered by performing

appropriate experiments. Notice however that we can draw one further conclusion

from the isotropy of the material, which is that failure cannot depend on the order

of the three stresses

. For example, if failure occurs at the point (a,b,c) it

must also occur at (b,a,c). It follows that the curve in Figure 2.7 must be symmetrical

about the 45

line

and additional symmetries of the same kind apply in the

three-dimensional envelope.

2.2.3 Ductile failure (yielding)

To proceed further, we need to consider separately the cases of ductile and brittle

materials, since they differ qualitatively in mechanism and behaviour.

Ductile materials suffer irreversible plastic deformation before fracture occurs.

Whether this constitutes failure depends on the speciﬁc design application, so to

avoid confusion, we shall refer to ductile failure as yielding and the corresponding

failure surface as the yield surface. Thus, if a component is loaded such that the

stress in some region passes outside the yield surface, it will not return to its original

state on unloading. A simplistic model of the distinction between elastic and plastic

deformation can be developed from atomic theory.

Consider ﬁrst a sphere resting on an undulating surface as in Figure 2.8 (a). When

unloaded, the sphere will rest at the bottom of the groove. Application of a horizontal

force will cause the sphere to move as shown in Figure 2.8 (b), but if the force is re-

moved slowly, the sphere will return to the bottom of the groove. This is an analogue

of elastic deformation. However, if a sufﬁciently large force is applied, the sphere

will be pushed over into the next groove and it will remain there even if the force is

40 2 Material Behaviour and Failure

removed. Once the critical force is reached, the sphere could be pushed over many

grooves, producing much larger displacements than are possible in the elastic range.

Notice also that when the sphere is being pushed down into the next groove, the sys-

tem is unstable. We could remove the force at this point but the sphere would keep

moving and would be left oscillating under gravity about the equilibrium position in

the next groove.

(a)

(b)

Figure 2.8: The sphere and groove model — (a) unloaded equilibrium position, (b)

displacement due to a horizontal force

Now consider a piece of material as a large assembly of atoms or molecules held

together under the inﬂuence of interatomic forces. When there is no external load,

the assembly will adopt an equilibrium position.

Application of external forces will

cause the atoms to make small relative motions to a new equilibrium conﬁguration.

However, sufﬁciently large forces might cause an atom or a block of atoms to jump

into a new conﬁguration, analogously with the movement from one groove to the next

in Figure 2.8. In this case, removal of the load will not cause the system to return to

its original conﬁguration and when the forces are removed, some of the atoms will

be left vibrating about their new equilibrium positions. The kinetic energy associated

with this vibration cannot be recovered through the external forces during unloading

and in fact has already been converted to heat.

Calculations of the force needed to move one block of atoms relative to another

grossly overestimate the theoretical yield stress in shear. In reality, crystal structures

are generally not geometrically perfect, but contain local defects known as dislo-

cations. Near the dislocations, the interatomic distances differ from the theoretical

value for a regular structure and a considerably smaller force is needed to make a

pivotal atom move to a new equilibrium position.

We shall argue in Chapter 3 that this can also be seen as a minimum energy conﬁguration,

as it clearly is for the sphere at the bottom of the groove in Figure 2.8 (a).

Recall that the distinction between a hot body and a cold one is that the atoms or molecules

in the hot body are vibrating with larger amplitude about their mean position.

J.E. Gordon (1968), The New Science of Strong Materials, Princeton University Press,

Princeton NJ, pp.91–98.

2.2 Failure theories for isotropic materials 41

Change in volume

Elastic deformation usually involves a change in volume or dilatation. For example,

the increase in length of a bar in uniaxial tension will more than compensate for

the reduction in diameter due to Poisson’s ratio, leading to an increase in volume

except in the special case of a material for which

= 0.5. In the atomic model, this

corresponds to a stretching of the interatomic bonds, so that the average interatomic

distance is increased.

If we load a body into the plastic range and then remove the load, the ﬁnal shape

will differ from the original shape, but there is no reason to expect the volume of

the body to have changed, since the average interatomic distance is governed by

similar equilibrium arguments in both original and ﬁnal states. This is conﬁrmed

by experiments which show that plastic deformation does not generally cause any

change in volume.

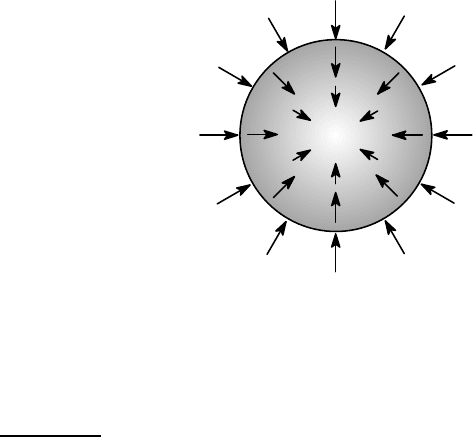
Figure 2.9: Sphere loaded by uniform compressive tractions

A corollary of this result is that stress states causing no change of shape cannot

result in plastic deformation regardless of their magnitude. Consider for example a

solid sphere of material loaded by a uniform external pressure p as shown in Figure

2.9. Because of symmetry, we would expect the sphere to remain spherical,

but to

It must be emphasised that this conclusion relates to a comparison of the volume before

loading and after unloading. Consider a uniaxial tensile test in which a specimen is loaded

into the plastic range and then unloaded. The unloading process is elastic and will involve

a reduction in volume. If the material yields at constant stress, the increase in volume

during the elastic phase of the loading process will be exactly equal to the decrease during

unloading and there will be no change in volume during the plastic phase of the process.

However, if the material work hardens (i.e. the yield stress increases with plastic strain), the

unloading process will occur over a larger stress range than the elastic phase of the loading

and will involve correspondingly more change in volume. The ﬁnal volume will still be

equal to the initial volume and therefore some increase of volume is associated with work

hardening during the plastic phase of the process.

Strictly, we should allow the possibility that the body deviates from sphericity under the

load. However, it can be shown that the work done by the uniform applied tractions must be

42 2 Material Behaviour and Failure

get smaller under the inﬂuence of the pressure. Thus, there is no change in shape —

only a change in volume — and so no plastic deformation can be involved. In princi-

ple, we should be able to increase p as much as we like without causing yielding to

occur. Perhaps more surprising is that the same argument would apply if the tractions

were tensile instead of compressive — i.e. if we could exert a uniform tensile trac-

tion on the surface of the sphere. Engineers have been quite ingenious

in trying to

verify this conclusion by experiment. Such results as are obtained suggest that tensile

failure eventually occurs, but in an essentially brittle manner (i.e. by propagation of

microcracks) even for usually ductile materials.

Hydrostatic stress

If we argue from symmetry that the stresses in the sphere of Figure 2.9 depend only

on the distance R from the centre, equilibrium arguments can then be used to show

that the stress state everywhere is deﬁned by

=−p — i.e. the three prin-

cipal stresses are equal to the applied uniform tractions (remember that compressive

stresses are negative by deﬁnition). Referring back to Figure 2.5, we conclude that

the three Mohr’s circles will reduce to the single point

=−p and that the maximum

shear stress will be zero. This latter conclusion can also be obtained from equation

(2.30).

The case where the three principal stresses are equal and there are no shear

stresses is referred to as a hydrostatic state of stress. The name arises because this is

the only stress state that can be sustained by a ﬂuid at rest. Recall that the constitu-

tive law for a ﬂuid relates the shear stress to the velocity gradient (for a Newtonian

ﬂuid, these quantities are proportional and the constant of proportionality is deﬁned

as the viscosity). If the ﬂuid is at rest, the velocity and the velocity gradient are both

zero and hence there must be no shear stress. Notice also that when the three Mohr’s

circles condense to the point

=−p, the normal stress on all planes must be equal to

−p. This constitutes a proof of the well-known result in hydrostatics that the pressure

at a point in a ﬂuid at rest is equal in all directions.

It is no coincidence that an example chosen to exhibit no change of shape under

load involves no shear stress. Shear stress causes shear strain, which in turn is deﬁned

in terms of the change in angles between faces of an element of material.

Changes

of angles necessarily involve change of shape, so the only states in which there is

no change in shape during deformation are those in which the stress is everywhere

hydrostatic.

zero under a constant volume plastic deformation. Since plasticity is a dissipative process,

it can only occur when the body deforms in such a way as to allow the external loads to do

work, so we can still conclude that plastic deformation is impossible in the sphere loaded

by a uniform pressure.

It is far from easy to apply a sufﬁciently large uniform tensile traction to the surface of

a body. Generally, the load application mechanism introduces areas of non-uniform stress

which serve as yield sites.

See §1.5.3 and Figure 1.6.

2.2 Failure theories for isotropic materials 43

The arguments of the preceding sections lead to the conclusion that yielding

should never occur under hydrostatic stress, regardless of its magnitude, and hence

that the complete straight line

should lie within the safe region for the

three-dimensional yield envelope. The two most important yield theories used for

ductile materials both meet this condition.

Tresca’s maximum shear stress criterion

Since plastic deformation involves irreversible shear strain and cannot occur if there

are no shear stresses, an obvious hypothesis for yielding is that it will occur when

the maximum shear stress reaches a critical value

— i.e.

max

≡ max



−



. (2.31)

The elastic region is then deﬁned by the inequality

max

. This is known as the

maximum shear stress theory or Tresca’s yield theory.

Tresca’s theory has one major advantage and one disadvantage. The governing

equation at the yield envelope is linear in the stresses and hence leads to linear equa-

tions which are algebraically easy to solve. However, the fact that

max

is the largest

of three quantities can be inconvenient. Generally we shall know enough about the

probable stress state to know which Mohr’s circle will have the largest radius, but this

choice makes it necessary to think about the problem carefully rather than applying

the criterion mindlessly. This opens up the possibility of error and it also makes for

complication when the theory is used as part of a numerical algorithm.

Von Mises’ deviatoric strain energy criterion

An alternative theory due to von Mises states that yielding will occur when the strain

energy density associated with the shear stresses reaches a critical value. This con-

cept requires some preliminary discussion before the criterion can be formally enun-

ciated.

When an element of material is loaded elastically, the applied tractions do work

which is recovered on unloading. In the loaded state, it is natural to think of this

energy as being stored in the material as strain energy.

Consider an inﬁnitesimal element of material of volume

V =

z, over

which the stresses

can be considered uniform. The stress

acts over a surface

z and hence corresponds to a force

F =

z .

The relative displacement of the two opposite faces experiencing this force is

= e

and hence the contribution to the strain energy is

44 2 Material Behaviour and Failure

U =

z =

V .

Similar results are obtained for the other stress components and lead to the expression

U =

(

+ 2

)

for the strain energy contained in the volume

V . The strain energy density U

deﬁned as the strain energy per unit volume and is therefore

(

+ 2

) .

Hooke’s law [equations (1.7–1.9, 1.12)] can be used to express this result in terms

of stresses only in the form

−2

(

)

+ 2(1 +

)





. (2.32)

If the Cartesian axes x,y,z are chosen to coincide with the principal directions, this

expression reduces to the simpler form

(

) −2

(

)

. (2.33)

Early researchers argued that a material could only store a limited amount of

strain energy per unit volume before yield occurred, but this leads to a criterion that

conﬂicts with the conclusion that yield cannot occur under hydrostatic stress. This

difﬁculty can be overcome by decomposing the actual stress state into a hydrostatic

mean stress

and a deviatoric stress

, deﬁned by

, (2.34)

where

≡

(2.35)

−

(2.36)

−

(2.37)

−

. (2.38)

Substituting these expressions into (2.33) and using the result

= 0

which can be veriﬁed by adding (2.36–2.38), we can write U

in the form

We cannot simply assume that the total strain energy density will be the sum of the values

obtained on substituting

and

respectively into equation (2.33), since the equation is