Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

Material Behaviour and Failure

Most calculations in mechanics of materials are performed in order to predict

whether a given component will fail in service or to determine dimensions or other

design speciﬁcations to ensure that the probability of failure is acceptably low.

An engineering component may be said to fail when it does not perform its spec-

iﬁed function. For example, if a bridge over a river deﬂects so much under load that

we get our feet wet when crossing it, the design is a failure, even though the bridge

returns to its original conﬁguration after the load is removed. In this chapter, we

shall use the more restrictive concept of material failure corresponding to situations

in which an irreversible change occurs in the material in response to the applied stress

ﬁeld. Major categories of material failure include ductile failure or yielding, where

the component does not return to its original state on unloading, brittle failure or

fracture, where an originally coherent structure breaks apart catastrophically, and fa-

tigue, where a progressive failure develops as a result of many cycles of loading and

unloading. We shall see below that yielding is largely determined by the maximum

shear stress and fracture by the maximum tensile stress in the body.

Brittle failure and fatigue failure are characterized by the separation of the body

into two or more pieces and are therefore always catastrophic, but yielding simply

implies that the body is permanently deformed and this may or may not be acceptable

in a given design application, depending on the function of the component. For ex-

ample, if the crankshaft of an internal combustion engine is permanently deformed, it

will cause additional dynamic loads due to out of balance mass, misalignment of the

pistons in the cylinders and misalgnment of the bearings and hence rapidly precipi-

tate more serious damage to the engine. By contrast, a limited amount of permanent

deformation of the members of a bridge structure may be acceptable. In the latter

case, a more efﬁcient design can often be achieved by analyzing the behaviour of the

structure in the plastic r´egime and applying appropriate safety factors.

In order to predict whether a component will fail under a given load, we must

ﬁrst estimate the stresses at potentially critical areas and then compare them with the

results of standardized material tests, such as the uniaxial tensile test. This procedure

We shall see applications of this procedure in Chapters 5 and 10 below.

J.R. Barber, Intermediate Mechanics of Materials, Solid Mechanics and Its Applications 175,

2nd ed., DOI 10.1007/978-94-007-0295-0_2, © Springer Science+Business Media B.V. 2011

26 2 Material Behaviour and Failure

is based on the argument that failure is a localized process involving irreversible be-

haviour at a particular point in the component. The material in the immediate vicinity

of the failure site that participates in the process can only be inﬂuenced by local con-

ditions. A particle of material embedded in a beam has no way of knowing whether

the tensile stresses it experiences are the result of bending or tensile loading and

therefore the tensile stress at failure will be the same for both modes of loading.

Thus, differences in global loading conditions can only inﬂuence the material be-

haviour insofar as they inﬂuence local conditions. Stresses are arguably the most

important determinant of material failure, but other local quantities can be signif-

icant. For example, the yield stress may be temperature-dependent, in which case

local temperature will feature in the yield criterion.

For a simple loading geometry, the failure load can be determined by comparison

with experimental results that produce a similar state of stress. For example, if a bar

is loaded in bending, the stress state is one of uniaxial tension and the behaviour of

the component can therefore be predicted using the results of uniaxial tensile tests.

In particular, plastic deformation will be predicted when the tensile stress reaches the

yield stress S

for the material.

However, many engineering components are subjected to more complex states of

stress involving both normal and shear components. The most general state of stress

involves six independent stress components — three normal stresses

and

three

shear stresses

. In principle, we might carry out tests to determine

the conditions at failure under all possible combinations of these components, but in

practice the experimental effort required would be enormous and the presentation of

the data would require volumes of tables or graphs. To put this in perspective, note

that, if failure depended on a single parameter (such as the maximum tensile stress),

one experiment would sufﬁce to determine it and the results could be presented as a

single numerical value. If there were two parameters, the results could be presented

as a graph or as a column of values. Three parameters requires a family of graphs

or a table. Imagine what we would need to present results with six independent pa-

rameters! In this section, we shall examine ways of reducing the complexity of the

problem, using a variety of arguments, assumptions and approximations. However,

we must ﬁrst review the relations between stress components in different coordinate

systems, in order to determine the most efﬁcient way of characterizing a given state

of stress.

2.1 Transformation of stresses

If the six stress components are known in a given Cartesian coordinate system x,y,z,

we can determine the corresponding components at the same point in a new system

′

by writing equilibrium equations for an appropriate inﬁnitesimal element of

material.

Strictly there are six shear stress components, but they are equal in complementary pairs

— i.e.

etc., as discussed in §1.5.1.

2.1 Transformation of stresses 27

2.1.1 Review of two-dimensional results

The reader should be familiar with this process for the simpler, two-dimensional case

in which the only non-zero stress components are

. However, this has

important consequences in failure analysis and it will therefore be useful to review

the more important results.

cos θ

sin θ

(a) (b) (c)

Figure 2.1: (a) Rotated coordinate system Ox

′

; (b) stress components; (c) force

components

Figure 2.1 (b) shows the side view of a triangular prismatic element which is

of constant thickness in the direction into the page. If the inclined face AB of the

element has unit area, the areas of the faces OB, OA will be cos

, sin

, respectively

and, for example, the force on OB associated with the stress component

will be

cos

. This and the forces associated with the other stress components are shown

in Figure 2.1 (c).

We can now sum the resolved forces in the directions x

′

respectively in Figure

2.1 (c) to obtain the equilibrium relations

′

cos

sin

+ 2

sin

cos

(2.1)

′

(cos

−sin

) + (

−

)sin

cos

. (2.2)

These are the two-dimensional stress transformation relations. They can also be writ-

ten in the double-angle form

′

−

cos2

sin2

(2.3)

′

cos2

−

sin2

, (2.4)

making use of well-known trigonometrical identities.

28 2 Material Behaviour and Failure

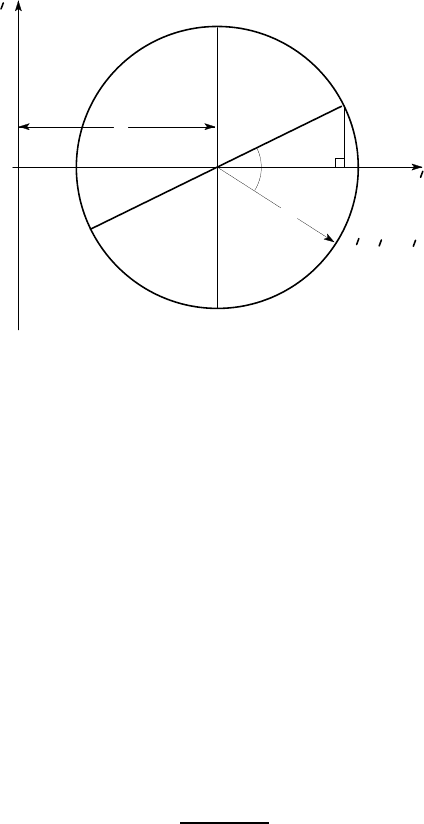
Mohr’s circle

If a graph is plotted comprising all points whose coordinates are

′

, with

as a

parameter, the resulting ﬁgure is a circle known as Mohr’s circle. Each point on the

circle corresponds to a particular value of

and hence to a particular inclination for

the plane AB in Figure 2.1 (b).

S(c,R)

S(c,-R)

X( , )

2θ

X ( , )

Y( ,- )

Figure 2.2: Mohr’s stress circle

The special case

= 0 corresponds to the face OB (the x-plane) and has coordi-

nates (

). This point is labelled X in Figure 2.2. As we increase

from zero,

the plane AB will rotate anticlockwise in Figure 2.1 (b), but the corresponding point

moves around the circle clockwise (i.e. in the opposite direction) in Figure 2.2, such

that the angle subtended at the centre of the circle is 2

. Thus, the point X

′

in Figure

2.2 corresponds to the plane AB in Figure 2.1 (b). If we were to make

/2, AB

would be horizontal in Figure 2.1 (b), but would face vertically downwards. It fol-

lows that in this case, we have

′

and

′

= −

. Notice the minus sign in

the expression for the shear stress on this plane, which is a consequence of the sign

convention used in Figure 2.1 (b) for x

′

,. Thus, the point Y corresponding to the

y-plane OA has coordinates (

,−

) in Figure 2.2.

The strategy for ﬁnding the centre of the circle and its radius is therefore as

follows:-

(i) Identify the points X(

) and Y (

,−

(ii) Draw the diametral line XY , which crosses the horizontal axis at the centre C of

the circle (c,0), where

c =

(

)

. (2.5)

(iii) The radius R of the circle can now be found using Pythagoras’ theorem on the

triangle CNX, with the result

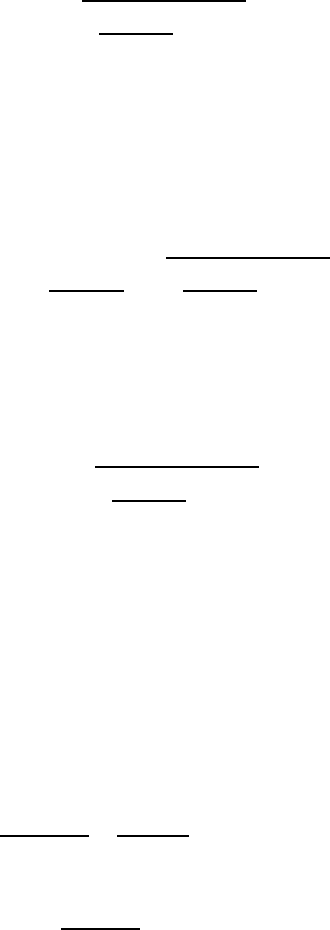
2.1 Transformation of stresses 29

R =



−



. (2.6)

Principal planes and principal stresses

Figure 2.2 enables us to draw the important conclusion that there exist two orthog-

onal principal planes, labelled 1,2, on which the shear stress

′

= 0. The normal

stresses

′

on these planes (the principal stresses

) are respectively the maxi-

mum and minimum values of normal stress. From Figure 2.2 we conclude that

= c ±R =



−



. (2.7)

Maximum shear stress

The maximum shear stress

max

corresponds to the points S in Figure 2.2 and hence

occurs on planes at 45

to the principal planes. Clearly

max

= R =



−



. (2.8)

Example 2. 1

The stress components at a point are

= 100 MPa,

= −20 MPa,

= −50

MPa. Find the principal stresses, the maximum in-plane shear stress and the angles

between the principal directions and the x-direction. Illustrate the inclination of the

principal planes with a sketch.

The points X(

) and Y(

,−

) are located as (100,−50) and (−20,50)

respectively, as shown in Figure 2.3 (a). The centre of the Mohr’s circle is therefore

at the point (40,0), since

c =

(

)

100 −20

= 40 MPa.

From the triangle CNX, we determine the radius of the circle as

R =

+ 50

= 78.1 MPa

and hence

= 40 + 78.1 = 118.1 MPa,

= 40 −78.1 = −38.1 MPa .

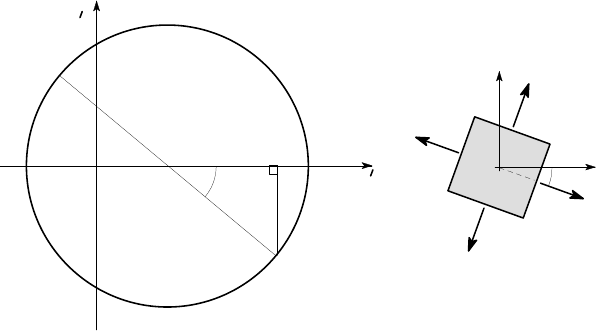
30 2 Material Behaviour and Failure

X(100, -50)

Y(-20,50)

(40,0)

118.1 MPa

-38.1 MPa

118.1 MPa

-38.1 MPa

19.9

(a) (b)

Figure 2.3: (a) Mohr’s circle; (b) orientation of the principal planes

To determine the inclination of the principal planes, we ﬁrst calculate the angle

in Figure 2.3 (a). The tangent of this angle is 50/60=0.833 and hence

= arctan(0.833) = 39.8

To get from X to 1 on the circle, we have to move 39.8

anticlockwise around the

circle. It follows that to get to the principal plane 1 from the x-plane, we must rotate

clockwise through half this angle — i.e.

= 19.9

Notice that we rotate the plane in the opposite direction to the rotation around

the circle. This deﬁnes the plane on which the larger principal stress

acts, as

shown in Figure 2.3 (b). Plane 2 is at right angles to plane 1 and hence corresponds

= 109.9

. Figure 2.3 (b) shows both principal planes in their correct orientation

and the principal stresses acting upon them.

2.1.2 Principal stresses in three dimensions

For the more general three-dimensional case there are six stress components

. The corresponding components in a new coordinate system can be

obtained by considering the equilibrium of the tetrahedron OABC of Figure 2.4, three

of whose faces lie in the x, y,z coordinate system and one normal to direction x

′

in a

new Cartesian coordinate system x

′

2.1 Transformation of stresses 31

Figure 2.4: Transformation of stress components in three dimensions

As in the two-dimensional case, there is a special choice of the coordinate system

′

— the principal directions — such that the three shear stresses

′

are all zero. The corresponding normal stresses are the principal stresses,

In this section, we shall show how the principal stresses and directions can be found

when the stress state is deﬁned in terms of the components

We deﬁne a set of unit vectors i, j, k corresponding to the Cartesian coordinate

system x,y,z. The tetrahedron of Figure 2.4 is drawn such that i, j, k are the out-

ward normals to the faces OBC, OCA, OAB respectively and the inward

unit vector

normal to the remaining inclined face ABC is denoted by p. We also deﬁne the three

direction cosines of p,

l = i · p ; m = j · p ; n = k · p , (2.9)

so named because they are the cosines of the angles between p and i,j,k respectively.

They are also the components of p in the three directions x,y,z and hence

+ m

+ n

= 1 , (2.10)

since p is a unit vector.

If the face ABC is taken to have unit area, the area of the face OBC will be

OBC = l , (2.11)

since OBC is the projection of ABC on the x-plane. Similarly, the areas OCA=m and

OAB =n.

Consider now the special case in which p is a principal direction and hence ABC

is a principal plane. The only stress component on this face is then a normal stress

in direction −p and it corresponds to a force −

p, since ABC has unit area. Equilib-

rium of the element in the three directions x,y, z then yields the three equations

The reader should compare with the two-dimensional Figure 2.1, where the positive x

′

direction is also the inward normal to the inclined face AB.

32 2 Material Behaviour and Failure

= l

+ m

+ n

(2.12)

= l

+ m

+ n

(2.13)

= l

+ m

+ n

(2.14)

Notice that the direction cosine on the left-hand side of equation (2.12) (for exam-

ple) comes from the resolution of the force −

p into the x-direction. By contrast,

the stress components

that appear on the right-hand side of this equa-

tion all act in the x-direction, but act on different areas OBC = l,OCA = m, OAB = n

respectively.

Considering (2.12–2.14) as a set of homogeneous equations for the direction

cosines l,m,n, we note that there will be a non-trivial solution if and only if the

determinant of coefﬁcients is zero — i.e.



(

−

)

(

−

)

(

−

)



= 0 . (2.15)

Expanding the determinant, we obtain the cubic equation

−I

+ I

−I

= 0 , (2.16)

where

(2.17)

−

(2.18)

−

+ 2

(2.19)

are known as stress invariants.

Equation (2.16) has three solutions, which are the three principal stresses

. When

takes any one of these three values, the three equations (2.12–2.14) are

not linearly independent — i.e. any one of them can be derived from the other two.

We can then determine the direction cosines deﬁning the corresponding principal

direction from (2.10) and any two of (2.12–2.14).

The set of equations (2.12–2.14) deﬁnes a linear eigenvalue problem, in which

is the eigenvalue and {l,m,n} is the eigenvector. Furthermore, the matrix of coef-

ﬁcients for this problem is the matrix of stress components in x, y, z and is therefore

symmetric. It follows from a well-known theorem in linear algebra

that the three

eigenvalues are all real and the three eigenfunctions mutually orthogonal. This lat-

ter result is equivalent to the geometric statement that the three principal directions

corresponding to

are orthogonal to each other.

Remember that equilibrium is a statement about forces, not stress components. Another

advantage of the double sufﬁx notation is that it reminds us that stress components are

associated with speciﬁc planes as well as directions.

See for example M. O’Nan (1976), Linear Algebra, Harcourt Brace Jovanovich, New York,

2nd edn., §7.2.

2.1 Transformation of stresses 33

Example 2. 2

The stress components at a point are

=−2 ksi,

=10 ksi,

=−5 ksi,

ksi,

=5 ksi,

=−3 ksi.

Find the three principal stresses and the direction cosines of the plane on which

the maximum tensile stress acts.

We ﬁrst calculate the three stress invariants, which are

= 3 ksi

−

= −143 (ksi)

−

+ 2

= 95 (ksi)

Substitution into (2.16) then yields the cubic equation

−3

−143

−95 = 0

for the principal stresses.

Some calculators and mathematical packages will be able to solve this equation

directly. Alternatively, we can use the closed form solution for cubic equations with

three real roots, which in the present case yields

−3I

cos(

) (2.20)

−3I

cos





(2.21)

−3I

cos





, (2.22)

where

arccos



−9I

+ 27I

2(I

−3I

)

3/2



. (2.23)

If the principal value of

= arccos(x) is deﬁned such that 0 ≤

≤

, the principal

stresses deﬁned by equations (2.20–2.22) will always satisfy the inequality

≥

(2.24)

and, in particular,

will be the maximum tensile stress.

Substituting the above numerical values for I

, we obtain the three principal

stresses

= 13.83 ksi,

= −10.16 ksi,

= −0.68 ksi .

The maximum tensile stress is therefore

= 13.83 ksi. To ﬁnd the direction

cosines of the corresponding plane, we substitute this value for

into any two of the

equations (2.12–2.14) and solve for the ratios l/n, m/n. For example, dividing (2.12,

2.13) by n, we have

34 2 Material Behaviour and Failure

(

−

)

= 0

+ (

−

)

= 0 ,

which constitute two simultaneous linear equations for the two unknowns l/n, m/n.

Substituting the numerical values for the stresses, we have

−15.83

+ 7

−3 = 0

−3.83

+ 5 = 0

with solution

= 2.01 ;

= 4.97 .

We now write equation (2.10) in the form

+ 1 = 29.75 ,

from which n= 0.183. The values of l,m are then recovered as

l =

×n = 2.01 ×0.183 = 0.368 ; m =

×n = 4.97 ×0.183 = 0.910 .

To summmarize, the principal stresses are

= 13.83 ksi,

= −10.16 ksi,

= −0.68 ksi

and the maximum tensile stress

acts on the plane deﬁned by

{l,m,n} = {0.368, 0.910, 0.183}.

Stress invariants

Equation (2.16) deﬁnes the principal stresses in terms of the stress components in any

convenient Cartesian coordinate system x, y,z. The principal stresses cannot depend

on the choice of x,y,z and hence, for a given state of stress, the same equation (2.16)

must be obtained regardless of the original choice of coordinate system. It follows

that the coefﬁcients I

in this equation must have the same value in all Cartesian

coordinate systems — in other words, that equations (2.17–2.19) deﬁne quantities

that are invariant under arbitrary rotation of the coordinate system (hence the name).

In particular, if we choose x,y, z to be aligned with the three principal directions, we

have

If we had taken the negative root n = −0.183, we would have obtained the eigenvector

{−0.368, −0.910, −0.183} which deﬁnes the same principal plane.