Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

1.3 Relative magnitude of different effects 5

ability to guess reasonably accurately. You will be surprised how often your guess is

close to the truth.

The moral of this rather laboured discussion is ‘Make a conscious effort to unlock

the door between your engineering thinking and your everyday experience’. You may

already have several years of engineering training, but you have a lifetime of hands-

on experience of the physical world.

1.2.2 Approximate solutions

The techniques described above can be used with some reliability to identify the

modes of deformation and failure of a loaded structure and hence determine a lim-

ited number of critical locations for which stress calculations are needed. The ac-

curacy of numerical estimates of failure loads etc. are less certain, unless one has a

wide experience of structures similar to that under consideration. At this stage, we

therefore generally wish to perform some mechanics of materials calculations. How-

ever, probably we are still considering a number of competing designs, so economic

considerations favour the use of idealized or approximate calculations wherever pos-

sible. In this context, a method that gives an accuracy of ±30% with 4 lines of cal-

culation is very much more useful than one that takes 4 pages of calculation to reach

an accuracy of ±5%. You should keep this in mind throughout the rest of this book.

Often the motivation for performing a more accurate (and hence extended) calcula-

tion is to establish the accuracy of the simpler procedure for future reference, or to

determine the range of parameters for which a simpler theory is sufﬁciently accurate.

For example, how ‘curved’ does a curved beam need to be before we need to take

the curvature into account, rather than assuming that the elementary straight beam

theory gives an adequate approximation to the stress distribution.

It is worth remarking that calculations of high accuracy are needed only when

the component in question is expected to operate fairly close to the maximum per-

missible load. An approximate calculation is often sufﬁcient to show either (i) that

even with a large overload, the component is far from the failure condition and hence

the design is not critical, or at the other extreme (ii) that the design condition is so far

above the failure load that the concept is not feasible without a major redesign. For

cases that fall between these extremes, we may be able to achieve an adequate factor

of safety by minor changes of geometry or material, but these are considerations that

will come into play only at a later stage of detail design, when the number of options

has been reduced.

1.3 Relative magnitude o f different effects

In many engineering components, stresses and displacements may result from several

different effects. For example, the automotive brake disc of Figure 1.2 may experi-

ence

This question is addressed in Chapter 11, §11.4.

6 1 Introduction

(i) surface loading (normal pressure and tangential (frictional) tractions) at the

brake pads,

(ii) bending due to unequal loading on the two sides of the disc balanced by support

loads at the disc centre,

(iii) self-weight of the disc,

(iv) loading associated with the centripetal acceleration during rotation,

(v) surface tractions due to air resistance (drag),

(vi) stresses associated with non-uniform temperatures due to frictional heating.

Figure 1.2: Automotive disc brake

A full analysis of all these effects threatens to make the design of even the sim-

plest component a major project. However, fortunately the stresses from one source

will usually dominate all the others, permitting them to be neglected. This important

principle is one of the few known exceptions to Murphy’s law.

It is used continually

by any experienced design engineer, but as far as I am aware has never been formally

enunciated. I therefore stake a tongue-in-cheek claim to immortality by deﬁning

Barber’s exception

If a component is subjected to several different kinds of loading process, the

relative magnitude of the resulting stresses will be such that only one of the processes

needs to be taken into account. The stresses from the remaining processes will usually

be within the range of uncertainty associated with this dominant process.

Furthermore, the difference in magnitudes is often so large that the simplest of

estimates is sufﬁcient to establish which loading process is dominant. If A = 1000 ×

B, estimates of A and B which might be in error by as much as a factor of 5 are still

sufﬁcient to establish that A ≫B.

In the formulation that everything will generally happen for the worst.

1.3 Relative magnitude of different effects 7

Example 1. 1

To illustrate this procedure, consider the various kinds of loading experienced by

the disc brake of Figure 1.2 and enumerated above. The disc will probably be made

of steel or cast iron, for which representative material properties are yield stress

≈30 −60×10

psi, Young’s modulus E = 30×10

psi, coefﬁcient of thermal

expansion

=7×10

−6

per

F, density

=0.284 lbs per in

(i) The hydraulic system will provide some magniﬁcation of the force applied at

the brake pedal, depending on the relative sizes of the hydraulic cylinders at

the pedal and the brake. However, with a brake pedal force of about 20 lbs, it

is unlikely that the force on a given brake pad could exceed 100 lbs (say) and

with a pad area of around 5 in

, this gives a nominal pressure of 20 psi which is

negligible.

(ii) Caliper brakes are supposed to exert equal forces on each side of the disc, so that

bending loads do not arise. If there is inequality, it should be substantially less

than the maximum brake force. To avoid calculations, imagine loading a typical

brake disc (say 10 in outside diameter, 5 in inside diameter and

in thick) by a

10 lb force and supporting it at the inner radius. It is inconceivable that this could

cause failure. Placing a disc between two supports and standing on it would exert

a force of 150 lbs (depending on your weight!) and would not be sufﬁcient to

cause failure. Thus, bending is not important.

(iii) Imagine the brake disc resting on the ﬂoor. Would you expect it to be weak

enough to fail under self weight? Obviously not. If you want to be more sci-

entiﬁc about this, you can estimate the stresses due to self weight by recalling

that the pressure in a ﬂuid under gravity is

gh if h is the depth below the free

surface. The same equilibrium arguments show that the pressure under (say) a

rectangular block of height h resting on the ground is

gh. For the disc, the

biggest dimension is the diameter and we calculate

0.284 ×10 ≈ 3 psi. This is

clearly negligible.

(iv) Think in the same way as in (iii), but replace g by the maximum centripetal

acceleration. At a road speed of 60 mph (88 ft/s), with a tyre diameter of 30

inches (2.5 ft), the rotational speed is (88/1.25) = 70 rad/s. The acceleration

is then

Ω

r = 70

×(5/12) ≈2000 ft/s

, compared with the gravitational accel-

eration of 32 ft/s

. Thus, stresses associated with acceleration are in the order

3×2000/32 ≈200 psi, which is still small.

(v) Stresses due to air resistance must be small. If they were even comparable with

those in (i) above due to the brake pad, the brakes would essentially be on all the

time!

(vi) Experience suggests that brake discs would be burning hot to the touch after a

severe stop (say ≈300

F). However, only temperature difference is important in

determining stresses here, since an unrestrained disc heated to a uniform temper-

ature will simply expand freely without stress. There will be differences in the

Notice that the gravitation constant g is already included in the weight when lbs are used

as the units, but would need to be included explicitly when working in SI units.

8 1 Introduction

heating and cooling rates at different radii, due to the higher speed at the outer

radius (linear speed is proportional to radius for a given rotational speed), but

the resulting temperature difference will probably not exceed ≈50

F, since steel

and cast iron are quite good conductors.

The order of magnitude of thermal stresses can be estimated as

≈E

α∆

T =

30×10

×7×10

−6

×50 ≈10×10

psi.

These ‘back of the envelope’ calculations tell us that the stresses due to temper-

ature difference are signiﬁcantly greater than the others, though still probably not

as high as the yield stress of the material. Since the loading is cyclic (stresses are

developed and then relaxed each time the brake is applied), there is a possibility of

fatigue failure resulting from thermal stresses and the above estimate is large enough

to justify a more exact calculation at a later stage in the design process.

All the other

loading processes can be neglected.

1.4 Formulating and solving problems

Once we have decided to perform some calculations to evaluate or specify a design,

we shall have to write governing equations deﬁning the appropriate physical laws

and other equations describing the geometry and the boundary conditions speciﬁc

to the system under consideration. It is always useful to examine ﬁrst where these

equations will come from, how many equations there are, how many unknowns,

and what sequence of mathematical steps will lead to the answer. In other words,

plan a strategy for the solution before you start performing any calculations. Don’t

memorize a set of solution procedures and then try to force every question into one

or other of them. There are always ways in which the question might be posed that

will elude these categories and engineering teachers are adept at ﬁnding them.

There is a signiﬁcant psychological dimension to solving problems accurately.

If you have total conﬁdence that the method you are using is going to work, you

will be much less likely to make errors during the solution. By contrast, if you have

a nagging feeling that you may have overlooked something in the formulation, you

will be distracted during the process and will probably make mistakes. This applies

in the real world as well as in the examination room.

1.4.1 Use of procedures

One of the most effective ways of improving your problem solving abilities is to

break the problem down into sub-tasks that can be treated as applications of standard

procedures. The word ‘procedure’ is used in a technical sense in computer program-

ming to denote a set of instructions that can be called into play when needed to per-

form certain operations and generate given results from a possible set of input data.

Methods of determining the thermal stresses in a heated disc will be discussed in Chapter

10. See Example 10.2 and Problem 10.3.

1.4 Formulating and solving problems 9

Programs organized with the use of procedures are much easier to understand and

trouble-shoot than those that are written ‘linearly’ — i.e. simply as a set of instruc-

tions in sequence. The same beneﬁts are obtained from treating mechanics problems

in a similar way.

For example, suppose we are given the cross section of a beam and the applied

bending moment M, and are asked to determine the maximum bending stress

max

Elementary bending theory tells us that this is given by

max

, (1.1)

where c is the maximum distance from the neutral axis and I is the appropriate second

moment of area.

However, in order to use this relation, we must ﬁrst ﬁnd c and I for the section.

We know that the neutral axis passes through the centroid of the section and the

location of the centroid is also needed in the determination of I. We might therefore

deﬁne the following simple procedures:-

: Given M,c,I, determine

max

from equation (1.1).

: Given the geometrical description of the section, determine the location of the

centroid.

: Given the geometrical description of the section and the location of the centroid,

determine c.

: Given the geometrical description of the section and the location of the centroid,

determine I.

When the problem is deﬁned in this way, it is clear that the output of P

and P

is required as input to P

and the output of P

is required as input to both P

and

. Thus, our strategy must be to perform P

ﬁrst, followed by P

and P

and then

, as shown schematically in Figure 1.3.

Figure 1.3: Strategy for determining maximum bending stress

The major beneﬁts of thinking this way are:-

(i) When we are planning the strategy for the solution, we can think of the pro-

cedures as single steps or building blocks in the development of the solution,

without having to concern ourselves with the details.

(ii) Conversely, when we are actually performing the operations inside one of the

procedures, we can temporarily erase from the mind the larger solution strategy

10 1 Introduction

and concentrate on the smaller task,

which is generally something that we are

completely conﬁdent we know how to do.

1.4.2 Inverse problems

Mechanics teachers are well aware of the fact that many different problems can be

generated from the same set of calculations by interchanging the order of the depen-

dent and independent variables. For example, in a given bending problem we might:-

(i) Give the dimensions of the cross section, the material and the loading and ask

for the factor of safety against yielding.

(ii) Give the loading and the maximum permissible tensile stress and ask for one of

the dimensions of the cross section to be determined.

(iii) Give the dimensions of the cross section and the maximum permissible tensile

stress and ask for the maximum bending moment that can be transmitted.

In more complicated problems, the number of permutations is enormous.

It is tempting in each case to try to devise a sequence of procedures that will start

from the given numerical data and lead by successive arithmetic calculations to the

desired result. However, algebra was invented to deal with precisely this problem.

The thinking here is ‘I don’t know how to solve this problem. If instead I were given

x,y,z and asked to ﬁnd a,b,c, I would be able to do it. Therefore, if I write x,y,z as

symbols, pretend that they are given and perform the calculations I know until I reach

expressions for a,b, c, I can then use the given values of the latter to deﬁne equations

for the unknowns’. Solving the equations may be a mathematical challenge, but (i)

we know that we need as many equations as there are unknowns, which provides

a check on the viability of the method and (ii) it is easier to lose conﬁdence in the

formulation of the mechanics problem than it is in the mathematical manipulations.

As a simple example, in the bending problem (ii) above we might denote the

unknown dimension of the cross section by d, ﬁnd the maximum stress in the beam

in terms of d and the given loading, and then equate it to the maximum permissible

tensile stress to obtain an equation that can be solved for d. Of course, this is a very

simple example, but the technique becomes more important when the overall com-

plexity of the problem is greater. A major advantage of using algebra to transform the

sequence in which the problem is solved is that we are thereby able to choose a se-

quence with which we are familiar, or for which we have a high degree of conﬁdence

of success.

It is interesting to note that procedures in computer programs generally adopt this same

‘restricted vision’. Variables deﬁned inside procedures have no deﬁnition outside the pro-

cedure and vice versa, unless an explicit ‘common’ deﬁnition is invoked. The more general

parallel between problem solving and programming is also instructive. Computer programs

have to be written so as to be completely ‘foolproof’ and it also makes sense to devise

problem solving techniques that are as immune as possible to our occasional periods of

intellectual weakness.

These days, many of the more routine mathematical operations can be performed in sym-

bolic languages such as Mathcad, Mathematica, MatLab and Maple.

1.5 Review of elementary mechanics of materials 11

1.4.3 Physical uniqueness and existence arguments

The problems which are easiest to formulate are those which mimic a conceivable

experimental situation. For example, a beam of given dimensions and material is

placed on simple supports and a given set of external loads is applied to it. The in-

formation given is sufﬁcient to enable someone to manufacture the beam and load it

in the laboratory. Suppose we imagine performing the experiment. In an ideal world,

the beam will behave in the same way each time, so we must presume that the given

information is sufﬁcient to deﬁne unique values for the moments, stresses and dis-

placements throughout the beam. More generally, whenever the information given

in the problem is sufﬁcient for the component to be manufactured (i.e. the dimen-

sions and material are completely speciﬁed) and loaded in the laboratory (the loading

conditions and history are completely speciﬁed), the mechanics problem must nec-

essarily be well-posed, since the resulting experiment can only logically have one

outcome.

‘Thought experiments’ of this kind give us conﬁdence that the given information

is indeed sufﬁcient for the problem to be solved.

In cases where the problem is

not posed in a manner that could form the subject of an experiment, it is helpful to

compare it with a related ‘experimental’ problem obtained by interchanging some of

the dependent and independent variables. In particular, make sure that the number

of unknowns in the ‘experimental’ formulation is equal to the number of additional

conditions given in the problem statement.

1.5 Review o f elementary mechanics of materials

We shall end this introductory chapter by brieﬂy reviewing some topics which we

assume the reader has already encountered in a ﬁrst course in mechanics of materi-

als. This material is covered in depth in the numerous excellent elementary texts, a

selection of which is listed under ‘Further reading’ at the end of this chapter. Many of

these topics will be revisited in the following chapters — indeed, one of the purposes

of more advanced study of the subject is to explore the limitations of the elementary

theories and to extend their range of application. This review will also serve to in-

troduce the notation that will be used for some of the more commonly occurring

quantities.

1.5.1 Deﬁnition of stress components

Stress is the force per unit area transmitted across an internal surface in the body.

It can be resolved into components, one normal to the surface (the normal stress)

There are some situations in mechanics where the loaded state is non-unique, notably those

involving elastic instability or buckling (see Chapter 12). However, this kind of behaviour

is generally unacceptable in service, so our interest in such problems is generally restricted

to determining the unique load at which buckling ﬁrst occurs.

As we explained above, having conﬁdence that the problem is well-posed is an important

factor in successfully solving it.

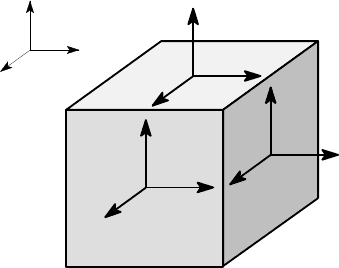
12 1 Introduction

and (in three dimensions) two shear stresses in the plane of the surface. If we set

up a local Cartesian coordinate system x, y, z such that the x-direction is the outward

normal from the surface in question, the normal stress component is usually denoted

and the two shear stresses by

, where the second sufﬁx denotes the

direction of the shear stress component. In more advanced work, it is usual to use

the symbol

for all stress components and a double sufﬁx notation, such that the

ﬁrst sufﬁx denotes the direction of the outward normal to the surface and the second

sufﬁx denotes the direction of the stress component. The quantities

would

therefore be written

. Notice that the x-plane (i.e. the plane normal to the

x-direction) can also be identiﬁed by an equation of the form x=constant.

With this notation, the stress components acting on a small rectangular brick ele-

ment of material are labelled as shown in Figure 1.4. Notice that the notation implies

that tensile normal stresses are positive and compressive stresses are negative.

Figure 1.4: Notation for stress components

It is often convenient to consider the components in the form of a stress matrix

σ ≡









. (1.2)

Equilibrium considerations demand that the shear stresses be equal in pairs (for ex-

ample

). This can be proved by taking moments about the three axes for the

element of Figure 1.4. It follows that the stress matrix (1.2) is symmetric. The equal

shear stress components

are referred to as complementary shear stresses.

One advantage of the double sufﬁx notation is that it lends itself to the use of matrix

methods in manipulating stress components in general problems.

In the following text, we shall generally use the double sufﬁx notation, but we

shall continue to use the symbol

without sufﬁces to denote shear stresses in situa-

tions where the direction of the stress is either obvious or not important (for example,

in Chapter 6).

1.5 Review of elementary mechanics of materials 13

1.5.2 Transformation of stress components

If all the stress components — i.e. all the elements of the stress matrix — are known

in a given Cartesian coordinate system, the corresponding components in rotated

coordinate systems at the same point can be determined from equilibrium consid-

erations. In two dimensions, the resulting equations permit a convenient graphical

representation known as Mohr’s circle. An important result is that there exists a spe-

cial Cartesian coordinate system — the principal axes — in which the corresponding

shear stress components are zero. We shall review these results in §2.1 and extend

them to the three-dimensional case.

1.5.3 Displacement and strain

The displacement of a point is a vector representing the distance moved by the point

during a process of deformation. Displacement will be denoted by the symbol u, with

sufﬁces to indicate direction where required. Thus, u

is the component of displace-

ment in the positive x-direction.

P Q

u (Q)

u (P)

x+ xδ

Figure 1.5: Relation between normal strain and displacement

Normal strain is deﬁned as the ratio extension/original length for an element of

material. It can also be written in terms of displacement. Consider the small element

PQ shown in Figure 1.5, which is subjected to tensile loading. The element may

extend, but it may also move in the x-direction as shown. If the two ends of the

element move the same distance, there will be no extension. More generally, the

extension is

∆

(Q)−u

(P). If the ends, P, Q are originally at the points x, x+

respectively, the original length of the element is

x and the normal strain can then

be written

∆

(x +

x) −u

(x)

Taking the limit as

x→0, we obtain

∂

. (1.3)

Recall that the mathematical deﬁnition of the derivative is

′

(x) = lim

x→0

f (x +

x) − f (x)

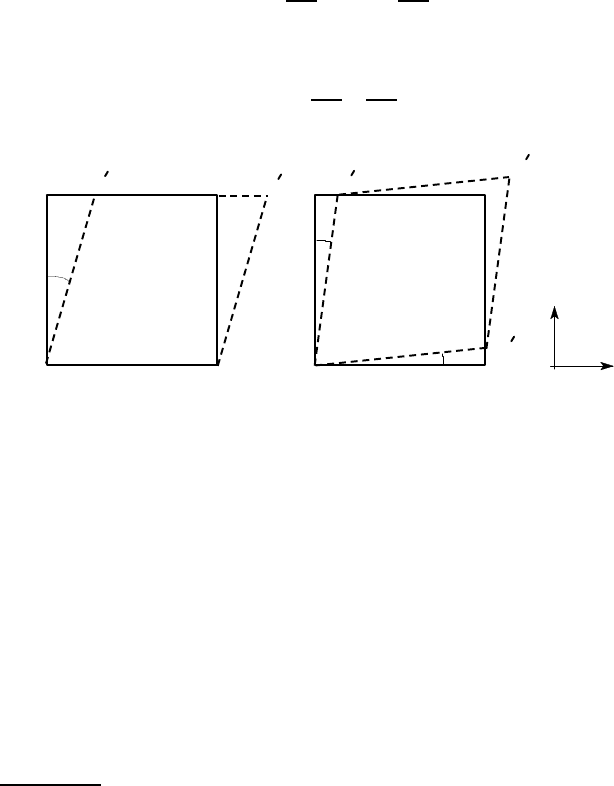
14 1 Introduction

Similar expressions can of course be written for

The shear strain

is deﬁned as the change (measured in radians) in the angle at

the corner of a rectangular element, as shown in Figure 1.6 (a). Notice that in general,

the element may both deform and rotate, as shown in Figure 1.6 (b), in which case

. It can be shown by geometric arguments that for sufﬁciently small

angles

∂

;

∂

(1.4)

and hence

∂

. (1.5)

(a) (b)

Figure 1.6: Geometrical deﬁnition of shear strain

As with stress, there is a double sufﬁx notation for strain which is helpful in the

matrix manipulation of general results. We use the symbol e for all strain components

and deﬁne e

and 2e

etc. Notice the factor of 2 in the deﬁnition of shear

strain.

The quantity e

is referred to as the mathematical shear strain in contrast

to the engineering shear strain

The factor of 2 is not introduced just to make the subject more confusing! It turns

out that many of the relationships between strains are simpliﬁed with the mathemati-

cal deﬁnition — notably those associated with strain transformation. The reader may

have noticed that the equations used to obtain strain components in a rotated coordi-

nate system (those associated with Mohr’s circle of strain) are almost the same as the

corresponding equations for stress transformation except for a mysterious factor of 2

The double sufﬁx notation is widely used in more advanced texts, particularly those con-

cerned with theoretical elasticity. Confusion is avoided by the universal use of

for engi-

neering shear strain and e or

for mathematical shear strain.