Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

2.3 Cyclic loading and fatigue 85

(i) Material properties

(a) S

=341 MPa.

(b) S

′

≈0.5 ×341 = 170 MPa.

= 0.8. The reliability is 50%, so C

= 1. Finally, to

estimate C

, note that the shaft diameter is 115 mm compared with 7 mm in

the standard test, so the stressed volume is larger by a ratio of about



115



= 4500 ,

suggesting a factor



4500



1/16

≈ 0.6 .

Thus,

= 1 ×0.8 ×0.6 ×170 = 82 MPa.

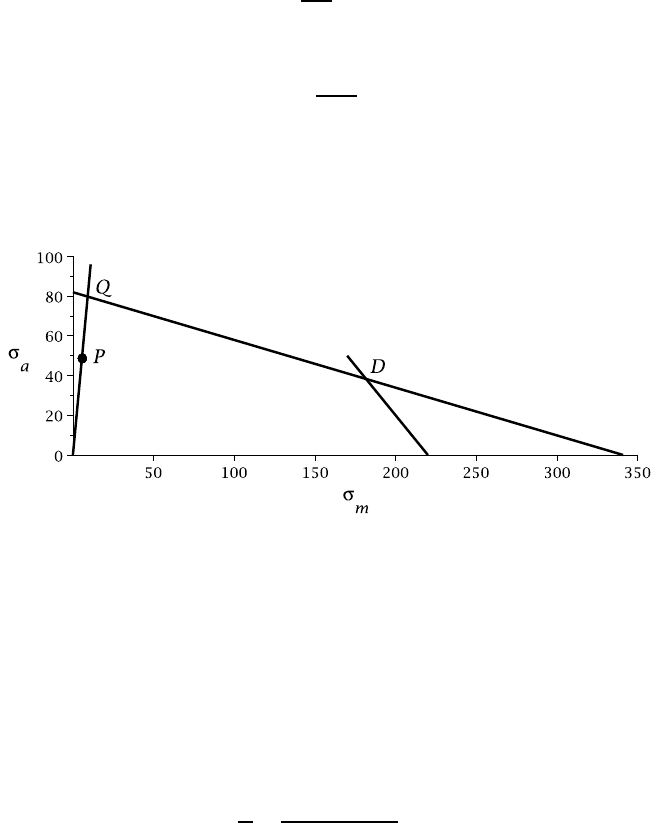
(d) The Goodman line is then constructed by joining the points (341,0) and

(0,82) as shown in Figure 2.38.

(MPa)

Figure 2.38: Goodman diagram for Example 2.10.

(e) From Figure 2.30, we have q≈0.7 for a steel with S

=341 MPa.

(ii) The 50 kN force generates a bending moment

M = 50 kN ×80 mm = 4 kNm.

The bending moment causes alternating stresses only, whilst the torque and axial

force cause mean stresses only.

(iii) (a) The nominal stresses are:-

Axial Force

−40 ×10

×4

×115

= −3.85 MPa

86 2 Material Behaviour and Failure

Bending

32M

32 ×4 ×10

×115

= 26.8 MPa

Torsion

16T

16 ×2 ×10

×115

= 6.7 MPa.

(b) For K

, we have

135

115

= 1.174 ;

115

= 0.035 ,

and hence, using Figures C.5, C.6, C.7 from Appendix C,

= 2.24 for axial loading, K

= 2.1 in bending and K

= 1.74 in torsion.

= 1 + (K

−1)q = 1.87 for axial loading

= 1.77 in bending

= 1.52 in torsion.

(d) For the axial force

= −3.85 ×1.87 = −7.2 MPa.

For the bending moment

= 26.8 ×1.77 = 47.4 MPa.

For the torque

= 6.7 ×1.52 = 10.2 MPa.

(iv) Alternating stresses arise only from bending and are given by

= 47.4 MPa.

Mean stresses arise from both the axial force and the torque. We have

= −7.2 MPa

= 10.2 MPa

and hence

= 5.3 MPa.

2.4 Summary 87

(v) The operating point P and the corresponding failure point Q are shown in the

Goodman diagram of Figure 2.38 above. The failure point can be determined by

solving the equations

341

= 1

representing the Goodman line and

47.4

5.3

representing the load line. We have

341

5.3

47.4

= 1

and hence

= 79.8 MPa

giving a safety factor

SF =

79.8

47.4

= 1.68.

(vi) We note that Q is well to the left of the point D, so no yielding will occur in the

stress concentration.

2.4 Summary

In this chapter, we have discussed the states of stress under which material failure

may be expected. In particular,

(i) A general state of stress can be characterized by the three principal stresses or

equivalently by the three stress invariants of equations (2.17–2.19). We have

developed methods of determining the principal stresses and the maximum shear

stresses from a general set of stress components.

(ii) Ductile failure or yield is associated with shear deformation without change of

volume and is best predicted by the von Mises criterion (2.43), according to

which yielding occurs when the distance in principal stress space of the point

(

) from the hydrostatic line (

) exceeds a critical value.

In design calculations, it is most conveniently implemented by comparing the

equivalent tensile stress (2.54) with the uniaxial yield stress for the material.

(iii) Brittle materials fail by crack propagation which in turn is driven by the exis-

tence of a critical stress intensity factor at the crack tip. This implies a maxi-

mum tensile stress theory of failure. If all the applied stresses are compressive,

considerations of crack face friction lead to the modiﬁed Mohr criterion. Full

characterization of a brittle material requires experimental measurements of the

strength in tension and in compression.

(iv) Under cyclic loading, fatigue failure can occur. The fatigue strength of a com-

ponent is signiﬁcantly affected by its size, the surface ﬁnish and the presence

of geometric stress concentrations. The superposition of a tensile mean stress

reduces the alternating stresses required to produce fatigue failure.

88 2 Material Behaviour and Failure

Further reading

Stress transformation and t heories of failure

A.P. Boresi, R.J. Schmidt, and O.M. Sidebottom (1993), Advanced Mechanics of

Materials, John Wiley, New York, 5th edn., Chapters 2,4.

J.E. Gordon (1968), The New Science of Strong Materials, Princeton University

Press, Princeton NJ.

F.A. McClintock and A.S. Argon (1966), Mechanical Behavior of Materials, Addison-

Wesley, Reading MA.

Fracture mechanics

M.F. Kanninen and C.H. Popelar (1985), Advanced Fracture Mechanics, Clarendon

Press, Oxford.

H. Leibowitz, ed. (1971), Fracture, An Advanced Treatise, 7 Vols., Academic Press,

New York.

Stress intensity factors and stress concentration factors

R.E. Peterson (1974), Stress Concentration Factors, John Wiley, New York.

W.D. Pilkey (1994), Formulas for Stress, Strain and Structural Matrices, John Wiley,

New York.

R.J. Roark and W.C. Young (1975), Formulas for Stress and Strain, McGraw-Hill,

New York, 5th edn. (Stress concentration factors only).

G.C. Sih (1973), Handbook of Stess Intensity Factors, Inst. of Fracture and Solid

Mechanics, Lehigh University, Bethlehem, PA.

Fatigue failure

J.A. Collins (1981), Failure of Materials in Mechanical Design, Wiley, New York.

R.C. Juvinall (1967), Stress, Strain and Strength, McGraw-Hill, New York.

R.C. Juvinall (1983), Fundamentals of Machine Component Design, Wiley, New

York, Chapter 8.

J.E. Shigley and L.D. Mitchell (1983), Mechanical Engineering Design, McGraw-

Hill, New York, 4th edn., Chapter 7.

Problems

Section 2.1

2.1. The stress at a point is deﬁned by the components

= −80 MPa,

= 10

MPa,

= 20 MPa. Sketch the corresponding Mohr’s circle and hence ﬁnd

the maximum in-plane shear stress and the orientation of the planes on which it acts.

Problems 89

Illustrate your answer with a sketch of an appropriately rotated rectangular element,

taking care to indicate the correct direction for the shear stress on these planes.

2.2. The stress at a point is deﬁned by the components

=7 ksi,

=10 ksi,

=−20 ksi. Sketch the corresponding Mohr’s circle and hence ﬁnd the maximum

in-plane shear stress and the orientation of the planes on which it acts. Illustrate your

answer with a sketch of an appropriately rotated rectangular element, taking care to

indicate the correct direction for the shear stress on these planes.

2.3. The stress at a point is deﬁned by the components

= 8 ksi,

= −10 ksi,

=−4 ksi. Find the principal stresses

and the inclination of the plane

on which the maximum principal stress acts to the x-plane.

2.4. The stress at a point is deﬁned by the components

=0 MPa,

=100 MPa,

= −40 MPa. Find the principal stresses

and the inclination of the

plane on which the maximum principal stress acts to the x-plane.

2.5. The principal stresses at a given point are

=−50 MPa,

=−50 MPa. Sketch

Mohr’s circle for this state of stress and hence determine the maximum in-plane shear

stress. Comment on your results.

2.6. The principal stresses at a given point are

=10 ksi,

=5 ksi. Sketch Mohr’s

circle for this state of stress and hence determine the maximum in-plane shear stress.

2.7. The principal stresses at a given point are

=10 MPa,

=−100 MPa. Sketch

Mohr’s circle for this state of stress and determine the normal stress on a plane in-

clined at an angle

to the principal plane 1. Hence ﬁnd the range of values of

for

which the normal stress is tensile.

2.8. The stress at a point is deﬁned by the components

=220 MPa,

= 0 MPa,

= −80 MPa,

= 40 MPa,

= 0 MPa. Find the three principal

stresses and the direction cosines of the plane on which the maximum tensile stress

acts.

2.9. The stress at a point is deﬁned by the components

= 120 MPa,

= −20

MPa,

=20 MPa,

=60 MPa,

=0 MPa,

=0 MPa. Find the three principal

stresses and the direction cosines of the plane on which the maximum tensile stress

acts.

2.10. The stress at a point is deﬁned by the components

=0 ksi,

ksi,

=−3ksi,

=−3 ksi,

=−3 ksi. Find the three principal stresses and the

direction cosines of the plane on which the maximum tensile stress acts.

2.11. The stress at a point is deﬁned by the components

= 20 ksi,

= 8 ksi,

= −15 ksi,

= 0 ksi,

= 4 ksi,

= 16 ksi. Find the three principal stresses

and the direction cosines of the plane on which the maximum tensile stress acts.

2.12. The strain energy stored per unit volume in a body subjected to a uniform state

of stress deﬁned by the principal stresses

90 2 Material Behaviour and Failure

(

) ,

where e

are the corresponding principal strains. Use the stress-strain relations

(1.7–1.9) to obtain an expression for U

in terms of the stress invariants and the

material properties. Hence show that if I

=0,

= −

2.13*. Show that

for all states of stress.

2.14*. Establish a condition that must be satisﬁed by the six stress components

if one of the principal stresses is to be zero and the other

two negative — i.e.

=0,

<0,

<0.

Hint: Solve the problem ﬁrst in terms of the stress invariants using equations

(2.25–2.27) and then substitute for the invariants in the ﬁnal conditions using (2.17–

2.19).

2.15. If the radii of the three Mohr’s circles in Figure 2.5 (a) are denoted by

respectively, show that



−3I



2.16. The stress at a point is deﬁned by the components

= 120 MPa,

= 300

MPa,

= 70 MPa,

= −80 MPa,

= 0 MPa, so that

is a princi-

pal stress. Find the other two principal stresses and sketch the three Mohr’s circles.

Hence determine the magnitude of the maximum shear stress.

2.17. The stress at a point is deﬁned by the components

= −20 ksi,

= 5 ksi,

= 2 ksi,

= 5 ksi,

= 0 ksi, so that

is a principal stress. Find the

other two principal stresses, sketch the three Mohr’s circles and hence determine the

magnitude of the maximum shear stress.

2.18. The stress at a point is deﬁned by the components

= 85 MPa,

= 320

MPa,

=100 MPa,

=−40 MPa,

=50 MPa,

=−20 MPa. Find the three

principal stresses, sketch the three Mohr’s circles and hence determine the magnitude

of the maximum shear stress.

2.19. The stress at a point is deﬁned by the components

= 5 ksi,

= 0 ksi,

=−8 ksi,

=−4 ksi,

=2 ksi,

=−2 ksi. Find the three principal stresses,

sketch the three Mohr’s circles and hence determine the magnitude of the maximum

shear stress.

Problems 91

Section 2.2.3

2.20. The uniaxial yield strength of annealed AISI 1015 steel is 386 MPa. Estimate

the shear stress at ﬁrst yield in the torsion test for this material using (i) Tresca’s

theory and (ii) von Mises’ theory.

2.21. Show that the radius of the cylinder in Figure 2.12 deﬁning the von Mises yield

surface is

2/3S

2.22. Show that the perpendicular distance d of a general stress point (

)

from the hydrostatic line in Figure 2.12 is given by d =

√

oct

2.23. A steel is found to yield in uniaxial tension at a stress S

= 205 MPa and in

torsion at a shear stress

=116 MPa. Which of von Mises’ and Tresca’s theories is

the most consistent with this experimental data.

2.24. The torsion of a circular cylinder produces a state of pure shear

, for which the

principal stresses are (

,−

,0). If ﬁrst yield occurs in the torsion test at a shear stress

, ﬁnd an expression for the equivalent shear stress

, deﬁned as that function of

the stress components that is equal to

on the von Mises yield surface.

2.25. A solid cylindrical bar of diameter D is subjected to a bending moment M and

a torque T . Use equations (1.17, 1.18) to ﬁnd the corresponding stresses and hence

obtain an expression for the equivalent tensile stress

according to von Mises’

theory.

2.26. A cylindrical tube of mean radius 1 in and wall thickness 0.1 in is subjected

to an internal pressure p = 300 psi and a torque T =2000 lb.in. The ends of the tube

are closed. Find the safety factor against yielding if the material yields in uniaxial

tension at S

=8 ksi and von Mises’ theory is used.

2.27. The stress components at a given point in an engineering component are es-

timated to be

= 4.1 ksi,

= 0 ksi,

= 0.9 ksi,

= −3.1ksi,

= 1.2 ksi,

= 0 ksi. Estimate the factor of safety against yielding using von Mises’ theory if

the uniaxial yield stress of the material is S

=17.2 ksi.

2.28. A solid cylindrical shaft is found to yield when subjected to a torque of 5 kNm.

An identical shaft is now subjected to a bending moment M. Find the value of M

that will cause yield assuming that (i) Tresca’s theory and (ii) von Mises’ theory of

yielding applies.

2.29. A cylindrical steel shaft is required to transmit a bending moment of 1000 Nm

and a torque of 2200 Nm with a safety factor against yielding of 3. If the steel has

a yield stress of 250 MPa, ﬁnd the minimum permissible diameter for the shaft. Use

von Mises’ theory of yielding.

2.30. A mass of 10 kg is suspended from the ceiling on a steel wire of 1 mm diameter

and 2 m length. The mass is now rotated through an angle

causing the wire to twist.

92 2 Material Behaviour and Failure

If the steel has a yield stress of 300 MPa and G = 80 GPa, estimate the maximum

value of

if there is to be no plastic deformation. Use von Mises’ theory of yielding.

2.31. The three principal stresses at a given point are

=60 MPa,

=−100 MPa,

= −10 MPa. If the material has a yield stress of 250 MPa, estimate the factor of

safety against yielding using (i) the maximum shear stress theory and (ii) von Mises’

theory.

2.32*. A series of experiments is conducted in which a thin plate is subjected to

biaxial tension/compression

, the plane surfaces of the plate being traction-

free (i.e.

=0). Unbeknown to the experimenter, the material contains microscopic

defects which can be idealized as a sparse distribution of small circular holes through

the thickness of the plate. The hoop stress around the circumference of one of these

holes when the plate is loaded in uniaxial tension

is known to be

θθ

(1 −2 cos2

) ,

where the angle

is measured from the direction of the applied stress. Show graph-

ically the relation that will hold at yield between the stresses

applied to the

defective plate if the Tresca criterion applies for the undamaged material.

Hint: The hoop stress due to biaxial stress can be constructed by superposition.

The maximum must occur at either

= 0 or

/2, depending on the relative

magnitude of

Section 2.2.4

2.33. AISI 403 stainless steel has a fracture toughness K

= 77 MPa

√

m and a uni-

axial yield stress S

= 690 MPa. If a component contains a random distribution of

through cracks up to 1 mm in length, determine whether it will exhibit ductile or

brittle behaviour in tension.

2.34. A machine component can be idealized as a strip of width 20 mm and thickness

2 mm. It contains a central crack of length 2 mm. Determine the maximum load that

the component can carry in tension without fracture if K

=50 MPa

√

2.35*. An NDE test method can detect through cracks of lengths greater than 2 mm.

A given component consists of a strip of width 30 mm and thickness 4 mm and is

subjected to an alternating load in service of 20 ±10 kN. The material has a frac-

ture toughness K

= 30 MPa

√

m. Laboratory experiments suggest that under these

conditions fatigue cracks grow exponentially according to the equation

a = a

exp(

t) ,

where t is the length of time in service in seconds, a

is the original crack half-length

at t =0 and

=10

−8

−1

. Determine the minimum frequency of NDE testing if brittle

failure during the intervening period is to be avoided.

2.36. A cylindrical beam of length L and diameter D is simply supported at its ends

and loaded by a central force F. If the material is brittle and fails at maximum tensile

Problems 93

stress S

, ﬁnd the force F at fracture. Use your results to estimate the tensile strength

of chalk by performing a simple test.

2.37. A ceramic rod of diameter 8 mm is loaded by an axial compressive force of 80

N and a torque T . Find the value of T at failure if the material satisﬁes the modiﬁed

Mohr theory of failure with S

=0.8 MPa, S

=2.4 MPa.

2.38*. A material exhibits brittle failure in uniaxial compression at a stress

−S

= 0. Sketch the corresponding Mohr’s circle and obtain a general ex-

pression for the quantity

S =

−

(−

)

as a function of the orientation

of the plane to the principal direction 1. Find the

value of

for which S is a maximum and hence show that if failure occurs when

max



1 +

−



Comment on the implications of your results for the orientation of the failure plane

in a uniaxial compression test.

2.39. A solid cylindrical shaft is found to fracture when subjected to a torque of 5

kNm. An identical shaft is now subjected to a bending moment M. Find the value of

M that will cause fracture assuming that the maximum tensile stress theory of failure

applies.

2.40. A cylindrical pressure vessel of diameter 2 m and wall thickness 20 mm is

subjected to an internal pressure of 20 bar (2 MPa). What is the maximum length

of longitudinal through crack that can be permitted with a safety factor of 3, if the

material has a fracture toughness K

=50 MPa

√

2.41. The stress components at a given point in an engineering component are es-

timated to be

= 4.1 ksi,

= 0 ksi,

= 0.9 ksi,

= −3.1ksi,

= 1.2 ksi,

= 0 ksi. Estimate the factor of safety against fracture using the modiﬁed Mohr

theory if the uniaxial tensile and compressive strengths are S

= 10 ksi, S

= 30 ksi,

respectively.

2.42. A brittle material is found to obey the modiﬁed Mohr theory of failure with

= 10 ksi, S

= 30 ksi. What value of the coefﬁcient of internal friction

is most

consistent with these values?

Sections 2.3.1, 2.3.2

2.43. A 1 in. diameter circular shaft is machined from AISI 1010 steel, for which

= 47 ksi. It is loaded in rotating bending and is required to resist fatigue failure

with a reliability of 99.9%. Estimate the maximum bending moment that can be

transmitted.

94 2 Material Behaviour and Failure

2.44. A high speed steel used for manufacturing twist drill bits is found experimen-

tally to have a hardness of 480 BHN. The drills have a ground surface ﬁnish. What

is an appropriate fatigue limit S

for a 2 mm diameter drill for 50% reliability?

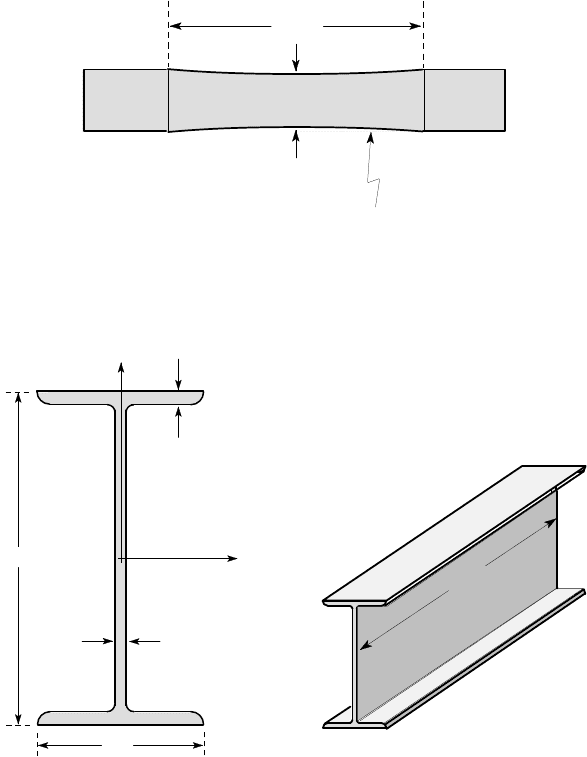
2.45*. Figure P2.45 shows the geometry and dimensions of the standard rotating

bending test specimen. Find the volume of material subjected to 95% or more of

the maximum alternating tensile stress. Perform a similar calculation for a bar of

1 in. square cross section and length 2 in. subjected to a reversed bending moment

M = M

cos(

t) and hence determine an appropriate value for C

for the bar.

0.3 in

radius 9.875 in

1.5 in

Figure P2.45

2.46. Figure P2.46 shows an I-beam of length 2m that is subjected to cyclic bending

about the horizontal axis. What is an appropriate value of C

to use in this case?

102

6.2

206

O x

2 m

all dimensions in mm

Figure P2.46