Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

3.10 Castigliano’s second theorem 155

3.10.4 Formal procedure for using Castigliano’s second theorem

Castigliano’s second theorem is so useful in structural problems that we here list the

steps in a formal way to make it easier to apply:-

(i) Put a dummy force (or moment) Q at the point and in the direction that the

displacement (rotation) component is required.

(ii) Use equilibrium arguments to determine the bending moments, torques etc.

throughout the structure.

(iii) Differentiate these expressions with respect to Q. Notice that the results are

identical to the bending moments, torques etc. due to a force (moment) Q of unit

magnitude acting alone.

(iv) Set Q = 0 in the bending moments etc. obtained at step (ii).

(v) Write down the total strain energy as a sum or integral in terms of the bending

moments, torques, axial forces etc, using equations (3.7, 3.24, 3.29, 3.31) as re-

quired. Do not substitute for these moments and forces or attempt to evaluate this

sum or integral at this stage. Leave any integrals in a symbolic form analogous

to (3.102).

(vi) Differentiate the expression for total strain energy with respect to Q.

(vii) Now substitute the results of steps (iii,iv) above (with Q=0) into this expression

and perform any summations or integrations that result.

3.10.5 Statically indeterminate problems

A statically indeterminate problem is one having one or more redundant supports

with corresponding unknown reactions that cannot be determined from equilibrium

considerations alone. Castigliano’s second theorem still applies to indeterminate

structures, but step (ii) of the procedure in §3.10.4 cannot be completed, because

the internal forces and moments in the structure cannot be found from equilibrium

arguments alone. However, the procedure can be easily adapted to indeterminate

problems and leads to a very efﬁcient solution.

The indeterminacy is associated with the fact that there are more unknown reac-

tions than can be found from the equilibrium conditions. The ﬁrst step is to replace

a sufﬁcient number of these reactions by supposedly known external forces that we

identify by a special symbol (say S

etc), in order to deﬁne an equivalent deter-

minate problem.

We can now use Castigliano’s second theorem to ﬁnd the displacements in this

modiﬁed problem and in particular to determine the displacements u

at the points of

application of S

The conﬁguration of the equivalent determinate problem and the original inde-

terminate problem will be the same, provided we choose the S

so as to make the u

There may be more than one way of doing this and hence the equivalent determinate prob-

lem is not unique. For example, if a beam is supported on three simple supports, any one

of the three may be replaced by an external force S to develop a determinate problem.

However, the ﬁnal solution will be independent of the choice made.

156 3 Energy Methods

zero, since then the points of application of the S

will not move and will be indis-

tinguishable from immovable supports. Once the S

are known, other features of the

solution can be obtained by further analysis of the equivalent determinate problem.

This, of course, is a general strategy for solving indeterminate problems. The

particular advantage of Castigliano’s second theorem is that it enables us to write the

condition u

=0 immediately in the form

∂

= 0 , (3.106)

where U is the strain energy in the equivalent determinate problem.

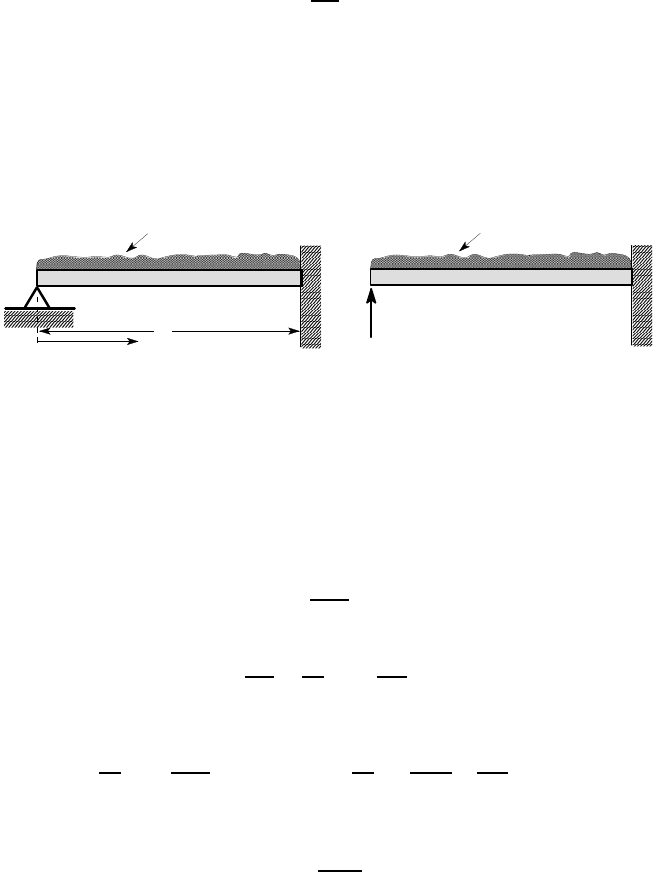
Example 3. 15 — The propped cantilever

The cantilever shown in Figure 3.36 (a), loaded by a uniform load w

per unit length,

is built-in at z = L and also simply-supported at the end z = 0. Find the reaction at

the simple support.

Figure 3.36: (a) The propped cantilever, (b) the equivalent determinate problem

There are three unknown reactions — a force and a moment at the built-in end

and a force at z = 0. We take the latter to be the redundant reaction S, which for

the purposes of the theorem is then considered to be a known external force. The

equivalent determinate problem is therefore deﬁned by Figure 3.36 (b)

The bending moment can now be written as

M =

−Sz (3.107)

and hence

u(0) =

∂

dz = 0 .

Substituting for M from (3.107), we obtain



−Sz



(−z)dz =



−



= 0

and hence the unknown reaction is

S =

. (3.108)

w per unit length

(a) (b)

3.10 Castigliano’s second theorem 157

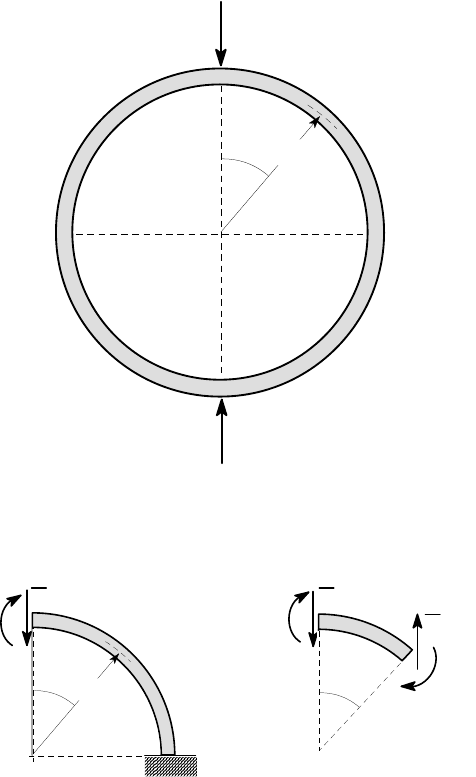
Example 3. 16: The curved bar

The complete circular bar of Figure 3.37 is compressed by equal and opposite forces

F, as shown. Determine the change in the diameter AC due to the two forces.

Figure 3.37: The circular ring compressed by two forces

The bar is symmetrical about both horizontal and vertical axes, so it is sufﬁcient

to consider the quadrant 0<

/2.

(a) (b)

Figure 3.38: One quarter of the circular ring

The symmetry boundary conditions ensure that there is no rotation at either end

of this quadrant, so we can treat the beam as built in at

/2 as shown in Figure

3.38 (a). By symmetry, we can also say that the shear force at

= 0 must be F/2,

but the moment S at that point is unknown and must be found from the symmetry

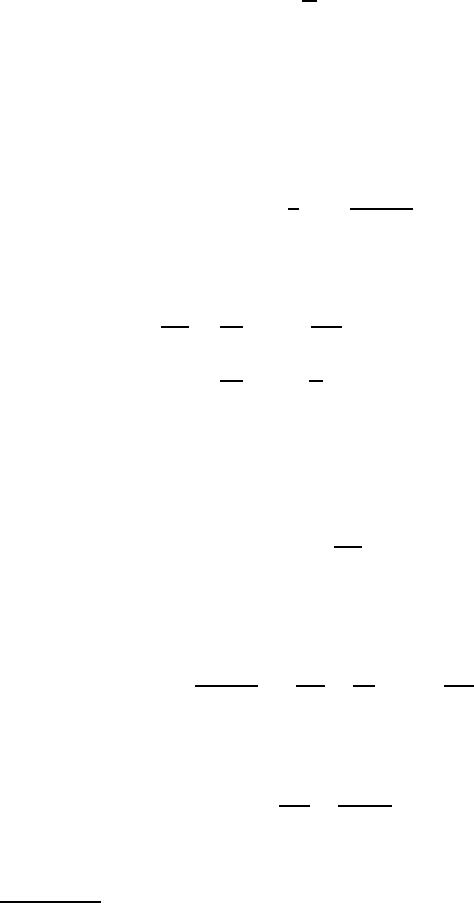
158 3 Energy Methods

condition that the slope of the beam must be zero at

= 0. This is what makes the

problem indeterminate.

Treating S as an external moment, we write the moment at a general point as

M =

Rsin

−S , (3.109)

using the free-body diagram of Figure 3.38 (b).

The equation for strain energy in the beam (3.24) has to be modiﬁed slightly here

because the beam is curved. The small element of beam length dL will be replaced

by the arc length Rd

and the quarter of the curved beam of Figure 3.38 (a) is deﬁned

by the range 0 <

/2. Thus, we have

U =

. (3.110)

Castigliano’s second theorem then states that the rotation at

=0 is

∂



Rsin

−S



(−1)Rd

using (3.109, 3.110).

This rotation must be zero by symmetry and hence, after evaluating the integral,

we obtain

S =

. (3.111)

We can now proceed to determine the vertical displacement u

of the point A in

Figure 3.38 (a), again using Castigliano’s second theorem. We have

∂

(F/2)

= 2

∂

Differentiating (3.109), we have

∂

Rsin

and hence

Notice that, as in other energy theorems, equation (3.97) may be modiﬁed by replacing the

force F

by a moment and the displacement u

by the corresponding rotation.

3.10 Castigliano’s second theorem 159



FR sin

−S



sin



−



We now substitute for S from (3.111), to obtain



−



= 0.0744

. (3.112)

If we assemble four quadrants like Figure 3.38(a) into the complete ring of Figure

3.37, it is clear that the diameter will change by 2u

, since the lower point B will

also move upwards by the same distance. Thus, the required change in diameter is

0.1488FR

/EI.

It is important to note that the Castigliano procedure is not applied to the in-

determinate problem as such. The ﬁrst stage is to identify redundant reactions and

then treat them as if they were external forces, thus deﬁning an equivalent determi-

nate problem. The Castigliano procedure is then applied to this determinate problem

throughout and the required results are only extracted at the end by substituting the

values of the artiﬁcial external forces S

that cause the corresponding support dis-

placements to be zero.

Most errors in the use of Castigliano’s second theorem for indeterminate prob-

lems occur in this initial process of deﬁning an equivalent determinate problem to

which the theorem can be applied. It is therefore important to take great care at this

stage. It might be helpful to try rephrasing the original problem, to make the relation

between the indeterminate and determinate problems clearer. For example, we could

rephrase Example 3.15 as follows:-

A cantilever beam of length L is built-in at z=L and subjected to a uniformly

distributed load w

and an end load S. Find the displacement at z = 0 and

hence ﬁnd the value of S if this displacement is to be zero.

3.10.6 Three-dimensional problems

So far, we have restricted attention to problems of plane structures that remain within

the plane during deformation. Three-dimensional structures, or plane structures that

deform out of the plane due to applied loads, can be analyzed by the same meth-

ods, but beam segments will then generally experience torques as well as bending

moments. The statical analysis of three-dimensional problems is also rather more

challenging, if only because of the need to sketch three-dimensional ﬁgures.

Example 3. 17

The L-shaped beam of Figure 3.39 is subjected to an out-of-plane load F. Find the

displacement u

of the end in the direction of the force.

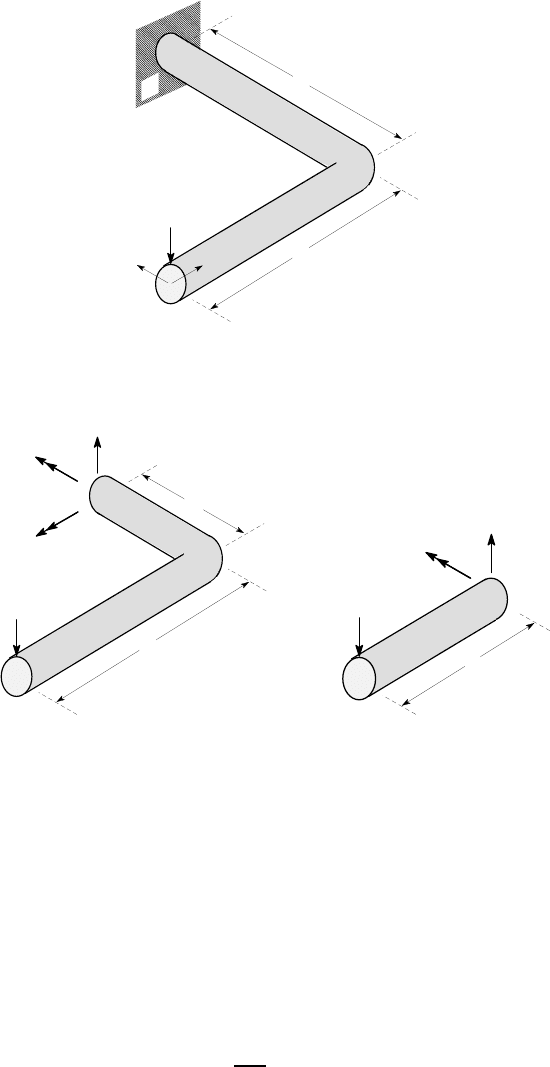
160 3 Energy Methods

Figure 3.39: The L-shaped beam subjected to an out-of-plane force

The corresponding free-body diagrams for the segments AB,BC are shown in

Figure 3.40.

(a) (b)

Figure 3.40: Free-body diagrams for the problem of Figure 3.39

Notice that the segment BC experiences a bending moment M

only, but the seg-

ment AB is in combined torsion and bending. Both segments also transmit a shear

force, but following the arguments of §3.3.5, we neglect the shear contribution to the

strain energy.

From equilibrium considerations, we have

= Fx in BC

= Fy ; T

= FL in AB. (3.113)

Thus, the strain energy in BC is

2EI

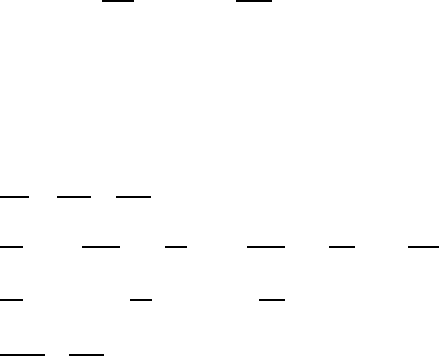
3.11 Summary 161

and that in AB is

2EI

dy +

2GJ

dy .

Notice that the contributions to U

from the bending moment and the torque are

simply added together, as explained in §3.3.3.

We could use either Castigliano’s second theorem or the method of §3.3 for this

problem, since there is only one external force. Using Castigliano’s second theorem,

we obtain

∂

dx +

∂

dy +

∂

dx +

dy +

2FL

3EI

, (3.114)

using equations (3.113).

3.11 Summary

As we discussed in Chapter 1, the stresses and displacements in an engineering com-

ponent are seldom critical in more than a few selected locations and success in engi-

neering design depends on being able (i) to identify these critical locations and (ii) to

estimate local stresses and/or displacements without an inordinate amount of calcu-

lation (in particular, without calculating the stresses and displacements everywhere

in the component). Energy methods are extremely versatile tools for this purpose.

In this chapter, we have introduced several variational methods based on the con-

cepts of strain energy and potential energy. The strain energy in an elastic structure

can be determined by devising a scenario in which the loads are slowly applied and

computing the work done on the structure. We have also introduced the idea of a

stiffness matrix relating the external forces and the corresponding displacements and

have shown by energy arguments that it must be symmetric.

The equilibrium conﬁguration of an elastic system is that which minimizes the

total potential energy (elastic strain energy + potential energy of external forces).

This result can be used to replace equilibrium arguments in the solution of problems.

It is particularly useful in engineering design in the sense of a Rayleigh-Ritz approx-

imation, to select the best values for parameters in an approximate description of the

kinematics of the deformation. The Rayleigh-Ritz method permits us to get a quick

estimate for the deformation and hence the internal forces and moments in a struc-

ture, particularly in cases where an exact analytical solution is either impractical or

162 3 Energy Methods

outside the expertise of the designer.

Notice that the method depends on the choice

of a good displacement function, which in turn requires us to practise the kind of

intuitive thinking discussed in §1.2.1. Rayleigh-Ritz arguments are also fundamental

to the ﬁnite element method, which is arguably the most used numerical method in

engineering design (see Appendix A).

Castigliano’s second theorem states that the derivative of the strain energy with

respect to an external force is equal to the local displacement in the direction of

that force. It is used in combination with an equilibrium analysis to determine the

displacement of one or more speciﬁc points without solving for the displacement

everywhere. It is particularly useful for indeterminate problems, where we need to

enforce the condition that one or more displacements at redundant supports are zero.

Further reading

T.M. Charlton (1973), Energy Principles in Theory of Structures, Oxford University

Press, London.

H.L. Langhaar (1989), Energy Methods in Applied Mechanics, Krieger, Malabar,

Florida.

K. Washizu (1975), Variational Methods in Elasticity and Plasticity, Pergamon, New

York, 2nd edn.

Problems

Sections 3.1, 3.2

3.1. Find the strain energy stored in a straight bar of rectangular cross section a ×b

and length L, subjected to a tensile force F, if the material has Young’s modulus E.

3.2. Find the strain energy stored in a solid circular cylindrical bar of diameter d and

length L, subjected to equal and opposite end torques T . The material has modulus

of rigidity G.

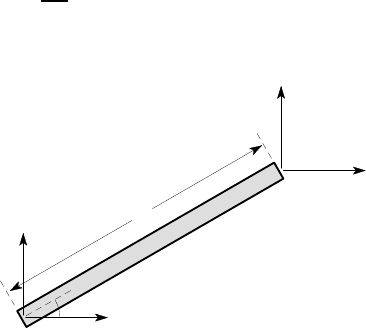
3.3 The ends A, B of the bar of Figure P3.3 are subjected to the displacements

as shown. Obtain an expression for the extension of the bar and hence

In the latter case, the reader’s ﬁrst reaction may be to seek out someone who does know

how to perform the calculation, such as a specialist stress analyst, but remember that we

must ﬁgure the time and money spent on this in our optimization process, as discussed in

§1.1.

Problems 163

show that the stored strain energy U is

U =

[(u

−u

)cos

+ (u

−u

)sin

]

where L,A are the length and cross-sectional area of the bar respectively and E is

Young’s modulus.

Figure P3.3

3.4 Two springs of stiffness k

respectively are connected in series. Find the stiff-

ness k of the two-spring system and hence ﬁnd the strain energy U stored when the

springs transmit a tensile force F. Then use equation (3.7) to ﬁnd the strain energy

stored in each spring separately (U

) and verify that the sum U

=U.

3.5. A spring is made of a non-linear material, such that the tensile force F and the

extension u are related by the equation F = F

tan(u/u

), where F

are constants.

Find the strain energy stored U (i) as a function of u and (ii) as a function of F.

Sketch the load-displacement curve and comment on the results when |u/u

| ≪ 1.

3.6. A cube of side a is subjected to tensile stresses

acting on the three

orthogonal faces. Use the elastic constitutive relations (1.7–1.9) to ﬁnd the relation-

ship between the forces on the cube and the corresponding displacements, and hence

ﬁnd the strain energy U stored in the cube.

3.7. In the system of Problem 3.4, suppose that one of the two springs is 100 times

stiffer than the other (i.e. k

= k, k

= 100k). Show that a good approximation to the

total energy stored U can be obtained by neglecting U

— the energy stored in the

stiffer spring.

Section 3.3

3.8. Find the displacement component u due to the inclined force F in Figure P3.8,

by equating the work done during loading to the strain energy stored in the springs.

Hence show that it reaches a minimum when

=105

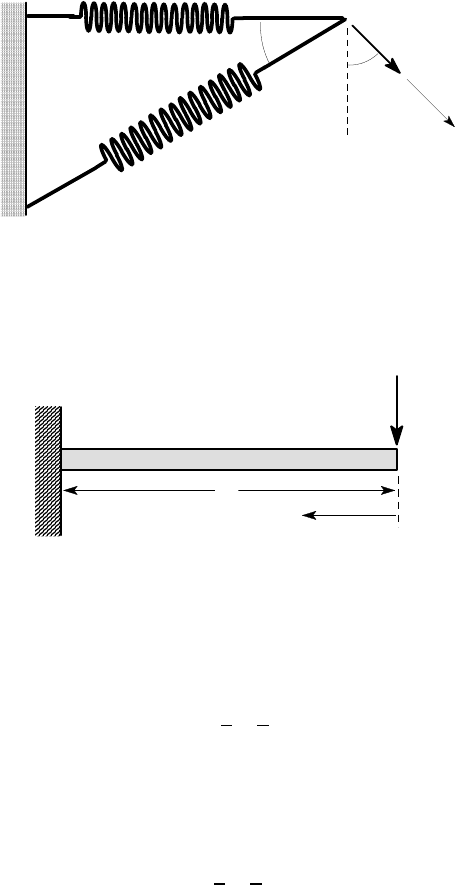
164 3 Energy Methods

Find also the angle

for which u is a maximum and the ratio u

max

min

Figure P3.8

3.9. Find the strain energy stored in the cantilever of Figure P3.9, subjected to a

concentrated force F at the free end. The beam is of solid square cross section, of

side c and is made of a material of Young’s modulus E.

Figure P3.9

Hence, determine the downward vertical deﬂection u under the load.

3.10. Suppose the cantilever of Figure P3.9 has a uniform width c, but its depth d

increases with distance z from the free end according to the equation

d = c





Find the second moment of area I as a function of z, the strain energy stored in the

beam and the deﬂection under the load.

Hint: You will ﬁnd it easier to perform the integration for the strain energy if you

make the change of variable

y =





3.11. Figure P3.11 shows a beam of length L and ﬂexural rigidity EI simply-

supported on two springs each of stiffness k. Use an energy method to ﬁnd the vertical

displacement u under the load. Hence show that if the dimensionless ratio