Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

Unsymmetrical Bending

The elementary theory of the bending of beams is restricted to the case where the

beam has a cross section with at least one axis of symmetry. In the present chapter,

we shall generalize the theory to beams of arbitrary cross section. All the remaining

assumptions of the beam theory will remain unchanged.

4.1 Stress distribution in bending

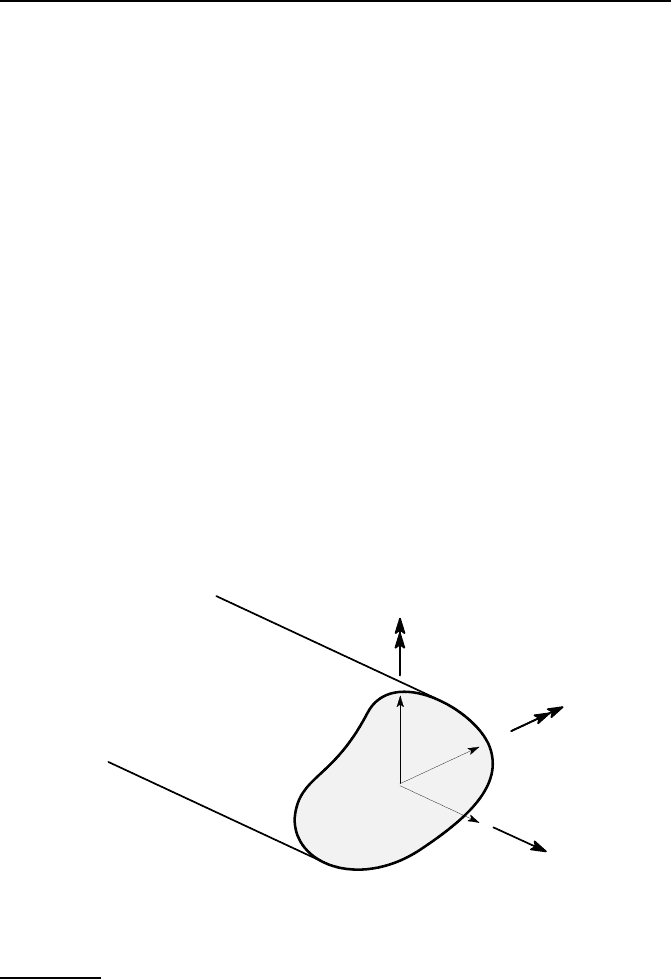
Figure 4.1 shows a beam of arbitrary cross section A, whose axis is in the z-direction

and which is loaded by an axial force F and bending moments M

. This ﬁgure

also serves to deﬁne the sign convention for moments, which are regarded as posi-

tive when the moment vector acting on the positive z-surface

is directed along the

positive x or y axes.

Figure 4.1: Coordinate directions and sign convention for axial force and bending

moments

i.e. the surface from which the z-direction is the outward normal.

J.R. Barber, Intermediate Mechanics of Materials, Solid Mechanics and Its Applications 175,

2nd ed., DOI 10.1007/978-94-007-0295-0_4, © Springer Science+Business Media B.V. 2011

186 4 Unsymmetrical Bending

4.1.1 Bending about the x-axis only

The moments M

will generally cause the beam to bend about both the x and

y-axes, resulting in radii of curvature R

, R

respectively. However, we ﬁrst restrict

attention to the simpler case in which there is no bending about y — i.e. R

= ∞, so

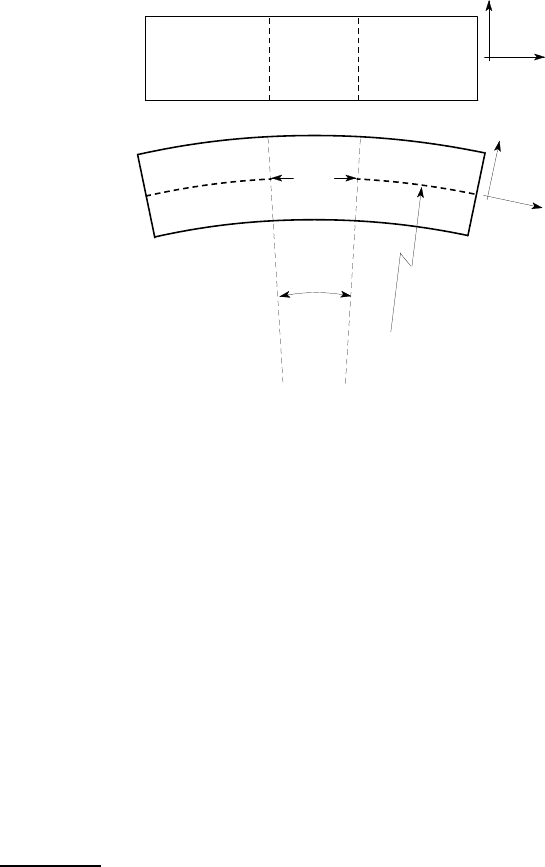
that two orthogonal views of the bent beam will be as shown in Figure 4.2.

Top view

Side view

(length)

(angle)

δθ

Figure 4.2: Orthogonal views of the beam bent only about the x-axis

We make the usual assumption of the beam theory that plane sections remain

plane.

Thus, a segment of beam bounded by two parallel cross-sectional planes AB

and CD in the undeformed state will deform as shown, such that there is a relative

rotation between AB and CD of angle

δθ

. If we extend the lines AB,CD in Figure 4.2,

they must therefore meet at a point O

, deﬁning the centre of curvature of the beam

in the yz-plane. In the segment ABCD, imaginary ﬁbres aligned in the z-direction that

were initially straight and all of the same length will become deformed into arcs of

circles whose lengths depend upon distance from this centre of curvature.

This implies that the axial strain e

is a linear function of y — i.e.

= Cy + D , (4.1)

where C,D are as yet unknown constants.

Equation (4.1) implies that there is a unique value of y at which e

= 0. This

deﬁnes a plane in the undeformed section which we call the neutral plane. Since the

origin of coordinates can be chosen arbitrarily, it is convenient to choose it to lie in

the neutral plane, which is then deﬁned by the equation y = 0. Equation (4.1) then

simpliﬁes to

We shall re-examine this assumption in §5.1 below in the more general context of an arbi-

trary non-linear constitutive law.

4.1 Stress distribution in bending 187

= Cy . (4.2)

We also choose to deﬁne the radius of curvature R

as the distance from the centre of

curvature O

to the neutral plane.

With these conventions, we can now determine the strain at any other point in the

section. We ﬁrst note that, by deﬁnition of the coordinate system, the original length

of the ﬁbre at y = 0 is the same as its ﬁnal length R

δθ

and this must be the original

length of all the ﬁbres in the segment ABCD, since AB,CD were originally parallel. A

ﬁbre which is a distance y from the neutral axis must deform into a circular segment

of radius (R

+ y) and hence have a deformed length (R

+ y)

δθ

. The axial strain of

such a ﬁbre is therefore

+ y)

δθ

−R

δθ

, (4.3)

showing that the constant C in (4.2) is equal to 1/R

If we assume that the normal stress components in the plane of the section are

zero (

=0), we then have

, (4.4)

where E is Young’s modulus. In other words, the axial stress is linearly proportional

to the distance from the neutral axis, as in the elementary theory.

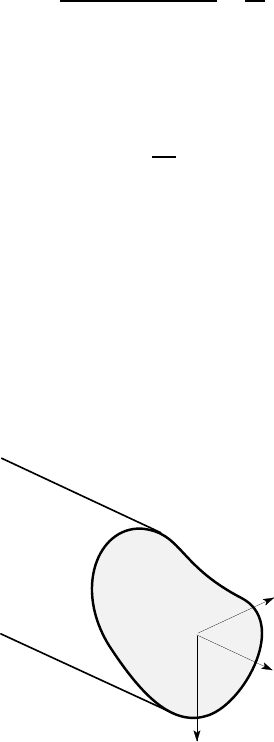
4.1.2 Bending about the y-axis only

Now suppose that instead of bending about the x-axis, we bend about the y-axis, with

radius of curvature R

. It is convenient to rotate the original view (Figure 4.1), so that

the axis of bending points in the same direction as in the previous section (see Figure

4.3). Notice, however, how this now makes the x-axis point downwards in the side

view as shown in Figure 4.4.

Figure 4.3: Beam bent about the y-axis

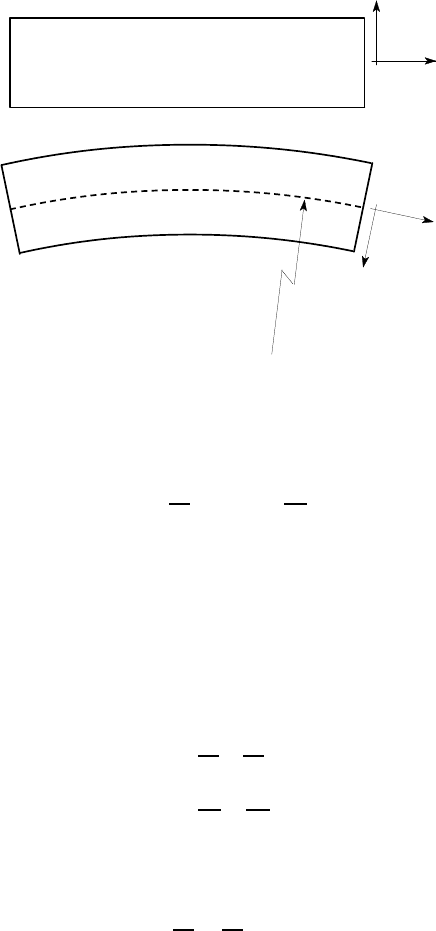
188 4 Unsymmetrical Bending

The convention used here is that in both cases, the curvature is such as would be

produced by a positive bending moment as deﬁned in Figure 4.1.

Top view

Side view

Figure 4.4: Beam bent about the y-axis

In other respects, the analysis is exactly similar to that for bending about the

x-axis and leads to the results

= −

;

= −

. (4.5)

The negative sign in these equations arises because the x-axis now points downwards

(i.e. towards the centre of curvature, rather than away from it), so that points with

positive x are in compression rather than tension.

4.1.3 Generalized bending

The most general kind of bending will involve curvature about both axes and can be

obtained by superposing these results — i.e.

−

(4.6)

−

. (4.7)

Notice that

is now a linear function of both x and y. We can again deﬁne a

neutral plane as the locus of all points where the strain e

and hence the stress

zero. This occurs when

, (4.8)

from (4.6) or (4.7). This equation is satisﬁed at the origin x = y = 0 and deﬁnes a

plane surface which is generally inclined to both x and y-axes.

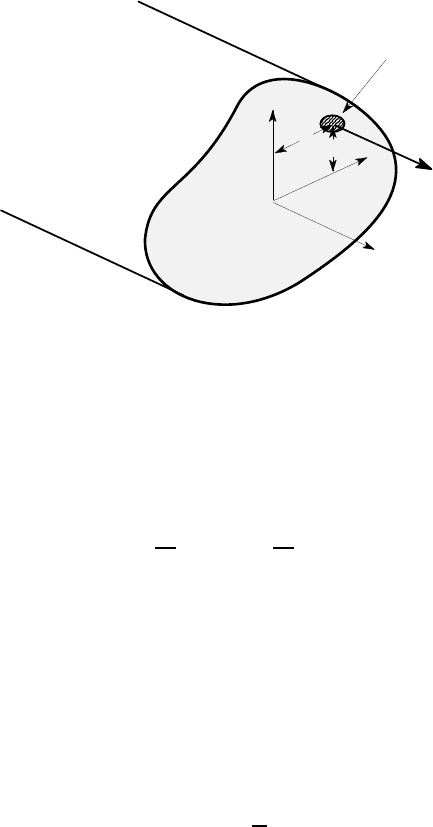
4.1 Stress distribution in bending 189

4.1.4 Force resultants

Consider now the forces and moments on the beam cross section, due to the stress

deﬁned by equation (4.7). There will in general be an axial force F as well as

bending moments M

about both x and y-axes.

δF = σ δA

δA

Figure 4.5: Elemental force due to

acting over

The normal stress

acting over the elemental area

A causes an elemental force

F =

A in the z-direction, as shown in Figure 4.5. The total axial force can be

found by summing these elemental forces over the cross section, with the result

F =

dA (4.9)

ydA −

xdA (4.10)

from (4.7). Notice that the summation leads to a double integral, since it is performed

over an area. For example, the element of area dA can be expressed in Cartesian

coordinates as the elemental rectangle dxdy and implies integration with respect to

both x and y over the area deﬁned by the cross section.

It is convenient to decompose the general bending problem into (i) a problem of

pure bending (F = 0) and (ii) a problem with purely axial loading (M

=0) and

then superpose the results. For the axial loading problem (ii), we assume that initially

plane sections remain parallel after deformation, in which case the stress is uniform

and given by

. (4.11)

Notice that the resultant of this uniform distribution must act through the centroid of

the area A.

For the pure bending problem (i), the condition F =0 can conveniently be satis-

ﬁed by choosing the coordinate system such that

190 4 Unsymmetrical Bending

xdA = 0 ;

ydA = 0 (4.12)

[see equation (4.10)], which is equivalent to choosing the origin of coordinates to

coincide with the centroid of the section A.

The bending moments M

are determined by summing the moments of the

elemental forces

dA about the x and y-axes respectively in Figure 4.5, with the

result

ydA (4.13)

= −

xdA , (4.14)

where the sign convention is as deﬁned in Figure 4.1.

Substituting for

from equation (4.7), we then obtain

dA −

xydA

dA −

yxdA .

Introducing the notation

dA ; I

xydA , (4.15)

these equations can be written

−

(4.16)

−

. (4.17)

4.1.5 Uncoupled problems

Notice that the ﬁrst term in each of equations (4.16, 4.17) is the same as that ob-

tained in the elementary theory of bending for symmetric beams. The quantity I

(known as the product second moment of area or product inertia) introduces cou-

pling between bending about the two axes. For example, a bending moment M

will

generally produce some bending about the y axis as well as the x-axis. However, in

the special case where I

= 0, there is no coupling and the general bending problem

reduces to the superposition of two applications of the elementary theory — one for

each moment component M

4.1 Stress distribution in bending 191

x, x

Figure 4.6: Section for which I

= 0 due to symmetry

We shall show in §4.4 below that all beam sections posess a pair of orthogonal

axes about which the product inertia is zero, but a commonly occurring case is that in

which either Ox or Oy is an axis of symmetry for the cross section. If this condition

is satisﬁed, for every element of area dA in the integral deﬁnition (4.15) there is an

equal element dA at the symmetric point for which one coordinate is the same and

the other is equal and opposite. Thus, for example, the two elements dA identiﬁed in

the section of Figure 4.6 make equal and opposite contributions to I

about any axis

system that includes the axis of symmetry Ox. It follows that the product inertia is

zero for this section about both of the systems Oxy, O

′

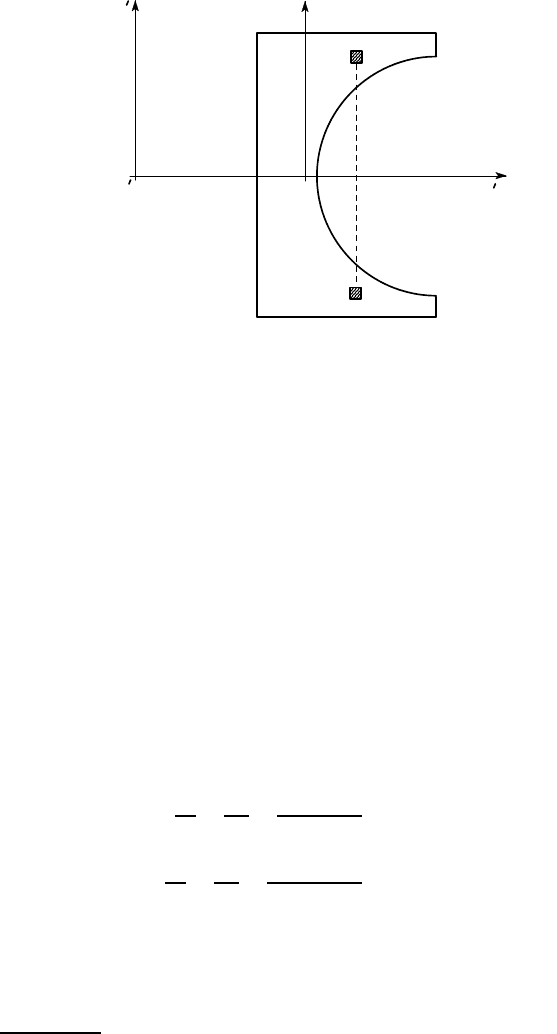
Example 4. 1

The channel section of Figure 4.7 is subjected to a bending moment with components

= 8 kNm, M

= 4 kNm. Find the maximum tensile stress due to bending, if the

appropriate second moments of area are I

=8.87×10

, I

=0.403×10

Since I

=0, there is no coupling and equations (4.16, 4.17) give

8 ×10

8.87 ×10

= 0.902 N/mm

4 ×10

0.403 ×10

= 9.926 N/mm

Substitution in equation (4.7) then gives

= 0.902y −9.926x

in MPa, if x,y are in mm.

Notice that 1 MPa=1N/mm

. Thus, if all quantities are expressed in the units of N and mm,

the ﬁnal expression for stress will be in MPa.

192 4 Unsymmetrical Bending

178

13.7

8 kNm

4 kNm

all dimensions in mm.

Figure 4.7

The maximum tensile stress will occur when y is at its maximum and x at its

greatest negative value — i.e. at the point A in Figure 4.7 deﬁned by

= −13.7 mm ; y

= 89 mm .

(Remember that x,y must be measured from the centroid.)

It follows that the maximum tensile stress is

max

= 0.902 ×89 −9.926 ×(−13.7) = 216.3 MPa .

4.1.6 Coupled problems

If I

6= 0, equations (4.16, 4.17) must be solved simultaneously for R

before

substitution in equation (4.7). This can be done in symbolic terms, with the result

+ M

−I

)

(4.18)

+ M

−I

)

, (4.19)

after which equation (4.7) gives

+ M

)y −(M

+ M

−I

)

. (4.20)

4.1 Stress distribution in bending 193

In particular, the general equation for the neutral axis (

=0) is

+ M

)y −(M

+ M

)x = 0 . (4.21)

We shall show in § 4.4.2 below that the expression (I

−I

), which appears in

equations (4.18–4.20) can never be zero — in fact it is always positive — so neither

the curvature nor the bending stress can be unbounded.

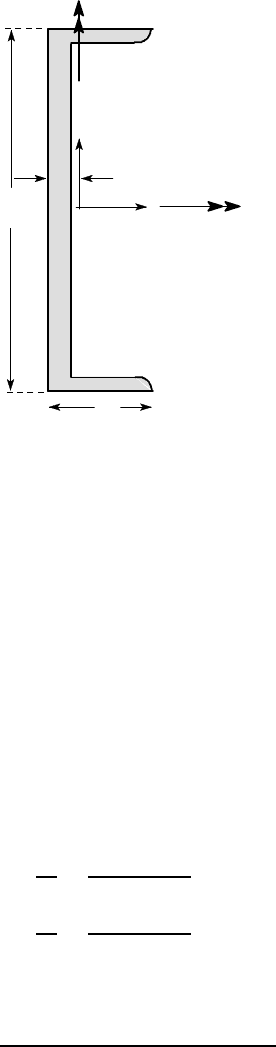
Example 4. 2

Figure 4.8 shows the cross section of a beam of length 2 m which is built in at one

end, the other end being subjected to a transverse load of 3 kN in the direction shown.

The centroid is located at the point O as shown and the appropriate second moments

of area are I

=1.33× 10

, I

=0.917×10

, I

=0.030×10

. Find the

inclination of the neutral axis and hence the location and magnitude of the maximum

tensile and compressive stresses.

all dimensions in mm.

Figure 4.8

The maximum bending moment will occur at the built-in end and is

M = 3 kN ×2 m = 6 kNm

about an axis inclined at 30

to the x-axis, as shown in Figure 4.9. This in turn can

be resolved into components

= M cos30

= 5.2 kNm = 5.2 ×10

Nmm

= M sin30

= 3 kNm = 3 ×10

Nmm .

3 kN

2000

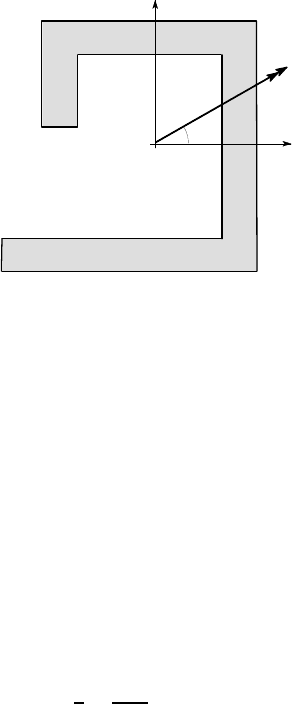
194 4 Unsymmetrical Bending

Figure 4.9

Evaluating the separate terms in (4.21), we have

+ M

) = 5.2 ×10

×0.917 ×10

+ 3 ×10

×0.03 ×10

= 4.86 ×10

Nmm

+ M

) = 3 ×10

×1.33 ×10

+ 5.2 ×10

×0.03 ×10

= 4.15 ×10

Nmm

The neutral axis is the line on which

+ M

)y −(M

+ M

)x = 0

— i.e.

4.86y −4.15x = 0

and hence

4.15

4.86

= 0.85 .

This deﬁnes a line inclined at

= tan

−1

0.85 = 40.5

to the x-axis, as shown in Figure 4.10.

We also have

−I

= (1.33 ×0.917 −0.03

) ×10

= 1.219 ×10

The maximum tensile and compressive stresses occur at the points furthest from

the neutral axis — i.e. at A and B in Figure 4.10. The coordinates of A are

= 28 −60 = −32 mm ; y

= 70 −35 = 35 mm ,

whilst for B

= 28 mm ; y

= −35 mm .