Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

4.2 Displacements of the beam 195

A (-32, 35)

B (28, -35)

40.5

Neutral axis

Figure 4.10

Substituting into equation (4.20), we therefore have

4.86 ×10

×35 −4.15 ×10

×(−32)

1.219 ×10

= 248 MPa (maximum tensile stress)

4.86 ×10

×(−35) −4.15 ×10

×28

1.219 ×10

= −286 MPa (maximum compressive stress) .

4.2 Displacements of the beam

In general, we expect the beam to have displacement components u

in both trans-

verse directions and, as in the elementary theory, these are related to the correspond-

ing radii of curvature through the equations

= −

;

. (4.22)

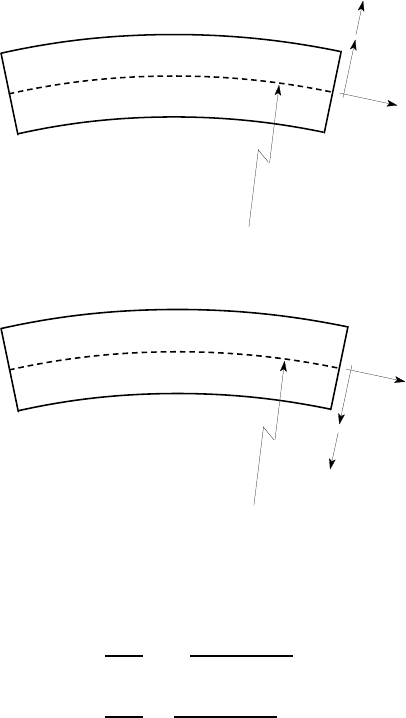
The sign convention here is chosen to conform with that introduced in Figures 4.2,

4.3 for R

, which is repeated here for convenience in the orthogonal views of

Figure 4.11 (a,b). Notice that u

are positive in the direction of the coordinate

axes x, y respectively and a positive value of the second derivative d

u/dz

implies

an increase of slope du/dz as we move in the z-direction.

196 4 Unsymmetrical Bending

(a)

(b)

Figure 4.11: Sign convention for radii of curvature and displacement components

Substituting for R

from equations (4.18, 4.19), we obtain

= −

+ M

E(I

−I

)

(4.23)

+ M

E(I

−I

)

. (4.24)

If the problem is determinate, M

can be found from equilibrium consid-

erations and equations (4.23, 4.24) can be integrated directly, as in the elementary

theory. The displacement components u

can therefore be found by independent

calculations. Notice however that if I

6=0, forces in the x-direction will tend to pro-

duce displacements in the y-direction and vice versa.

Example 4. 3

An L-section beam with second moments I

=1,512, 500 mm

, I

=412, 500 mm

, I

−450, 000 mm

and length 2 m is built in at one end and loaded by a vertical dis-

tributed load of 2 kN/m as shown in Figure 4.12. If the beam is made of steel with

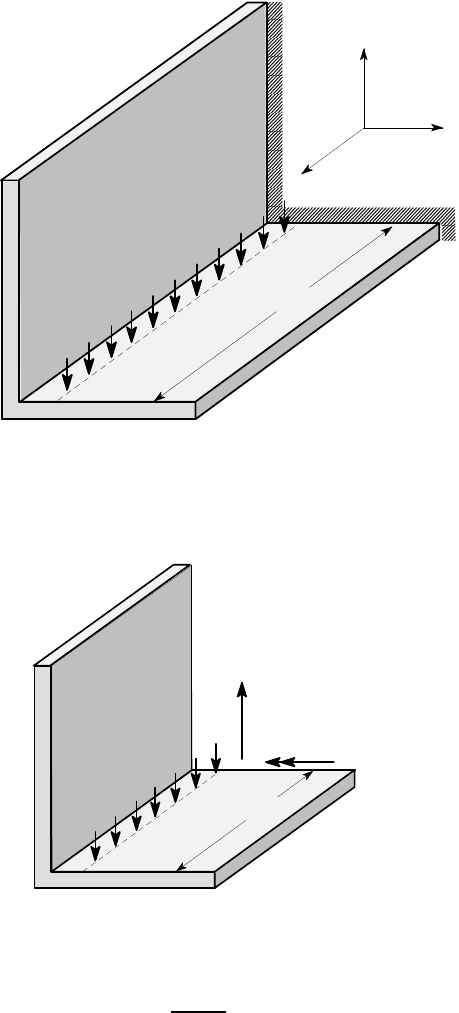
Young’s modulus 210 GPa, ﬁnd the displacement components at the free end B.

4.2 Displacements of the beam 197

Figure 4.12

We cut the beam at a distance z from A and draw a free body diagram, as shown

in Figure 4.13. Notice that M

acts in the negative x-direction on this cut, since the

cut surface is a negative z-plane — i.e. the z-direction is the inward normal.

(2 - z)

2 kN/m

Figure 4.13

Equilibrium arguments then yield the results

= 2000 ×(2 −z) ×

(2 −z)

= 1000(2 −z)

= 0 .

2 kN/m

2 m

198 4 Unsymmetrical Bending

We also have

E(I

−I

) = 210 ×10

(1,512,500 ×412,500 −450,000

) ×10

−24

= 88.5 ×10

−3

and hence equations (4.23, 4.24) give

= −

1000(2 −z)

×412, 500 ×10

−12

88.5 ×10

−3

= −4.662 ×10

−3

(2 −z)

−1

1000(2 −z)

×(−450, 000) ×10

−12

88.5 ×10

−3

= −5.086 ×10

−3

(2 −z)

−1

where u

,z are in metres.

Integrating the ﬁrst of these equations twice, we obtain

= −4.662 ×10

−3



4z −2z



+ A

= −4.662 ×10

−3



−



+ Az + B ,

where A,B are two arbitrary constants.

The beam is built in at z= 0 and hence

(0) = 0 ;

(0) = 0 ,

from which A= B =0.

The end deﬂection is then obtained by substituting z = 2 into the above expres-

sion, with the result

(2) = −4.662 ×10

−3



28 −



= −49.73 ×10

−3

m = −49.73 mm .

An exactly similar procedure for u

yields

= −5.086 ×10

−3



−



and hence

(2) = −54.25 mm .

Notice that the beam experiences a horizontal displacement, even though the

loading is purely vertical and in fact the horizontal displacement exceeds the vertical

displacement. Further insight into this behaviour is provided by the arguments of

§4.4.4 below.

4.3 Second moments of area 199

4.3 Second moments of area

The procedure developed so far requires that the second moments of area be given.

The properties of common structural sections such as I-beams, channels and angles

are standardized and tabulated in reference works, but many engineering applica-

tions involve non-standard beam sections for which the second moments must be

calculated.

The reader should be familiar with methods for evaluating I

, from the elemen-

tary theory of bending. However, since we need to extend these methods to include

the product inertia I

, we shall take the opportunity to give a brief review of the

complete procedure.

The direct method is to evaluate the double integrals in equation (4.15). This

process is demonstrated in Appendix B, but we seldom need to use it, since most

engineering beam sections can be decomposed into rectangular and circular sub-

areas, for which the appropriate properties are tabulated. However, these quantities

need to be referred to a set of axes through the centroid of the whole section, which

necessitates ﬁrst ﬁnding the location of the centroid and then transferring the second

moments to centroidal axes using the parallel axis theorem.

4.3.1 Finding the centroid

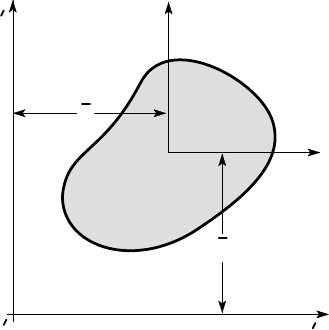
Consider the area A of Figure 4.14, deﬁned in the coordinate system O

′

. We

construct a parallel set of axes Oxy through the as yet unknown centroid O, deﬁned

such that

xdA = 0 ;

ydA = 0 . (4.25)

Figure 4.14: Centroidal and non-centroidal axes

From the geometry of Figure 4.14, the coordinates of a general point x

′

can be

written

200 4 Unsymmetrical Bending

′

= ¯x + x ; y

′

= ¯y + y , (4.26)

where ¯x, ¯y are the x

′

-coordinates of the centroid O. It follows that

′

dA =

( ¯x + x)dA = ¯x

dA +

xdA , (4.27)

since ¯x does not depend on the position of the elemental area dA.

The second integral in equation (4.27) is zero from (4.25) and

dA = A ,

′

dA = A ¯x or ¯x =

′

dA . (4.28)

By a similar argument

′

dA = A ¯y or ¯y =

′

dA . (4.29)

If the area A consists of a number of sub-areas A

, etc., whose areas and

centroids are already known, we can write

′

dA =

′

dA +

′

dA +

′

dA + ...

and hence

A ¯x = A

¯x

+ A

¯x

+ A

¯x

+ ... ,

where ¯x

, ¯x

are the x

′

coordinates of the centroids of the separate areas A

respectively. More generally, if

A =

∑

i=1

, (4.30)

then

A ¯x =

∑

i=1

¯x

; A ¯y =

∑

i=1

¯y

. (4.31)

4.3.2 The parallel axis theorem

The second moment of area I

′

about the non-centroidal axis O

′

is deﬁned as

′

′2

dA =

(y + ¯y)

dA ,

from equation (4.26). Expanding the integrand and taking the constant ¯y outside the

integral sign, we obtain

4.3 Second moments of area 201

′

dA + 2 ¯y

ydA + ¯y

dA . (4.32)

Now the second integral in (4.32) is zero from (4.25) and hence

′

dA + ¯y

dA = I

+ A ¯y

. (4.33)

By a similar argument we also have

′

= I

+ A ¯x

. (4.34)

These results deﬁne the parallel axis theorem for second moments of area. They

state that the second moment of area about any axis is equal to the corresponding

second moment about a parallel axis through the centroid of the area plus the product

of the area and the square of the distance between the two axes.

Since the terms A ¯x

,A ¯y

are always positive, it follows that I

′

is a minimum when

¯x = 0 — i.e. when O

′

coincides with Oy. In other words, the centroidal axes give

the minimum values of I

′

. Notice that it is essential that the second moments I

on the right hand sides of equations (4.33, 4.34) be centroidal.

A similar theorem can be proved for the product inertia I

. Deﬁning

′

dA =

(x + ¯x)(y + ¯y)dA ,

we have on expanding the product

′

xydA + ¯x

ydA + ¯y

xdA + ¯x ¯y

dA .

The second and third integral are zero because of (4.25) and hence

′

= I

+ A ¯x¯y . (4.35)

It is not the case that I

′

is a maximum at ¯x = ¯y = 0, since ¯x ¯y can be positive or

negative.

The parallel axis theorem can be used to determine the centroidal second moment

of area for a composite area A =

∑

i=1

. Suppose the centroid of the sub-area A

is located at ¯x

, ¯y

and that it has second moments of area I

about it’s own

centroidal axes. It follows from equations (4.33–4.35) that the contribution of A

the second moments about the communal centroidal axes through O(¯x, ¯y) will be

+ A

( ¯y

− ¯y)

, I

+ A

( ¯x

− ¯x)

, I

+ A

( ¯x

− ¯x)(¯y

− ¯y) ,

since the distance between the communal centroidal axes and the individual cen-

troidal axes are (¯x

− ¯x) and ( ¯y

− ¯y).

202 4 Unsymmetrical Bending

The second moments for the complete area will therefore be

∑

i=1

∑

i=1

( ¯y

− ¯y)

(4.36)

∑

i=1

∑

i=1

( ¯x

− ¯x)

(4.37)

∑

i=1

∑

i=1

( ¯x

− ¯x)(¯y

− ¯y) . (4.38)

These expressions are conveniently evaluated by constructing a table, as in the fol-

lowing example.

Example 4. 4

Determine the location of the centroid and the centroidal second moments of area

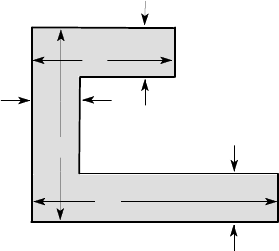
for the beam section shown in Figure 4.15.

all dimensions in mm.

Figure 4.15

We ﬁrst divide the area into sub-areas A

, as in Figure 4.16.

For the rectangle A

, we have

= 10 ×50 = 500 mm

and the centroid is located at the point O

with coordinates

¯x

= 25 ; ¯y

= 5 ,

relative to the point O

′

4.3 Second moments of area 203

5 mm

25 mm

Figure 4.16

Similar arguments for the areas A

enable us to complete the following table:-

i 1 2 3

500 200 300

¯x

25 5 15

¯y

5 20 35

Table 4.1

It follows from equations (4.30, 4.31) that

A = 500 + 200 + 300 = 1000 mm

A ¯x = 500 ×25 + 200 ×5 + 300 ×15 = 18,000 mm

A ¯y = 500 ×5 + 200 ×20 + 300 ×35 = 17,000 mm

and hence

¯x = 18 mm ; ¯y = 17 mm .

The centroidal second moment of area for a rectangle b×h is bh

/12 (see Ap-

pendix B), so we have

50 ×10

= 4167 mm

; I

10 ×50

= 104167 mm

where we note that the dimension cubed is that perpendicular to the required axis.

Using similar arguments for A

, we can therefore extend Table 4.1 to read

204 4 Unsymmetrical Bending

i 1 2 3

500 200 300

¯x

25 5 15

¯y

5 20 35

4167 6667 2500

104167 1667 22500

( ¯x

− ¯x) 7 −13 −3

( ¯y

− ¯y) − 12 3 18

Table 4.2

and hence, substituting the tabulated values into (4.36, 4.37), we have

= 4167 + 6667 + 2500 + 500 ×(−12)

+ 200 ×3

+ 300 ×18

= 184,333 mm

= 104167 + 1667 + 22500 + 500 ×7

+ 200 ×(−13)

+ 300 ×(−3)

= 189,333 mm

For the product inertia, we note that the individual rectangular areas have zero

product inertia about their own centroids by symmetry, so

= 500 ×7 ×(−12) + 200 ×(−13) ×3 + 300 ×(−3) ×18

= −66,000 mm

from (4.38).

4.3.3 Thin-walled sections

Many structural applications involve beams in which the thickness of the material

is small in comparison with the linear dimensions of the cross section. Examples

include structural steel sections, such as the channel of Figure 4.7 above, and also

beams formed by bending metal plate such as the angle irons available in hardware

stores and those used for supporting roadside signs.

Calculations in such cases can be simpliﬁed by describing the section in terms of

the mean line and the wall thickness, and by neglecting the ratio of thickness to linear

dimensions in comparison with unity. This is particularly advantageous in situations

where the general shape is known, but the dimensions have yet to be determined

from design considerations, since the approximation permits managable general ex-

pressions to be obtained in symbolic form.