Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

Problems 225

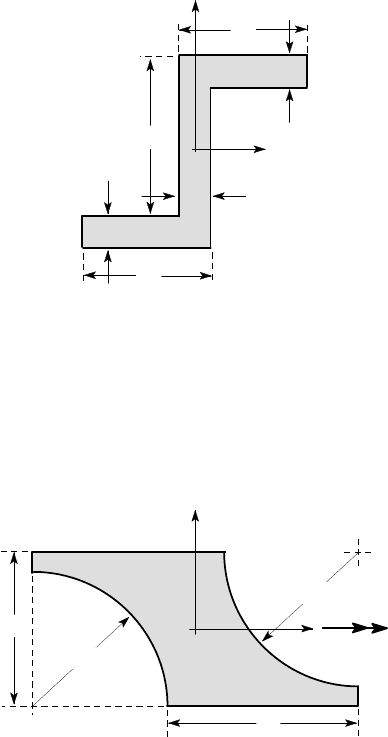
4.8. The Z-section of Figure P4.8 has second moments of area I

=560, 000 mm

, I

290, 000 mm

, I

=300,000 mm

. It is used for a beam of length 2m which is simply

supported at its ends and loaded by a uniformly distributed vertical load of 1000 N/m.

Find the location and magnitude of the maximum tensile stress.

all dimensions in mm.

Figure P4.8

4.9. The beam section shown in Figure P4.9 has second moments of area I

=317, 600

, I

= 791,700 mm

, I

= −298,500 mm

. The beam is subjected to a bending

moment M

= 1000 Nm about the x-axis as shown. Find the equation deﬁning the

neutral axis and hence the location and magnitude of the maximum tensile stress.

all dimensions in mm.

Figure P4.9

Section 4.2

4.10. Find the maximum horizontal and vertical components of the displacement for

the beam of Problem 4.8, if the beam is made of steel for which E = 210 GPa.

226 4 Unsymmetrical Bending

4.11. A beam with the triangular cross section of Figure P4.7 is of length L and made

of material with Young’s modulus E. It is built in at one end and loaded by a force F

in the x-direction at the other end. Find the two components of displacement at the

loaded end.

4.12. Figure P4.12 shows an L-section steel beam (E = 30×10

psi) with I

= 69.6

, I

= 11.6 in

, I

= −16.2 in

. The beam is 12 feet long, is simply supported at

its ends and is loaded by a vertical force of 1000 lbs as shown. Find the horizontal

displacement at the point of application of the load.

1000 lb

6 ft

Figure P4.12

4.13*. Figure P4.13 shows a beam with the cross section of Figure P4.9 loaded by a

uniformly distributed horizontal load of 1 kN/m. It is built in at A and the end B is

free to move horizontally, but is restrained from moving vertically by a frictionless

support. Find the vertical reaction and the horizontal displacement at B if the beam

is made of aluminium alloy for which E =70 GPa.

1 kN/m

2.2 m

Figure P4.13

Problems 227

Section 4.3

4.14. Calculate I

for the symmetric

Z-section of Figure P4.8 above.

4.15. Calculate I

for the section of Figure P4.9 above. You can use the results

from Example B.1.

4.16. Calculate I

for the L-section shown in Figure P4.16.

200

100

all dimensions in mm.

Figure P4.16 Figure P4.17

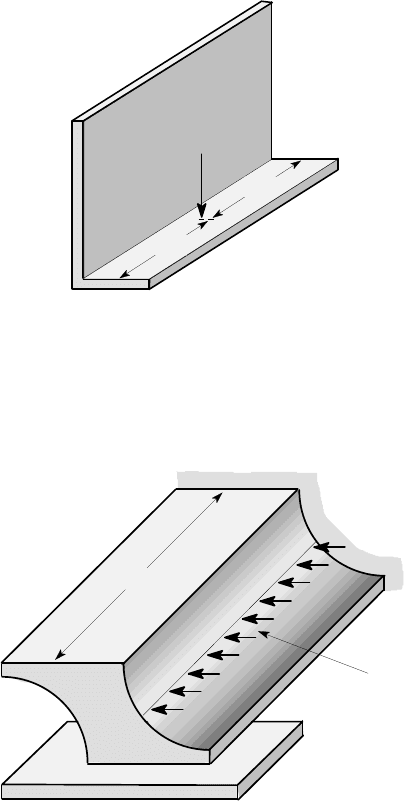
4.17. Find the product inertia I

for the beam section shown in Figure P4.17. Notice

that the centroid must be at O by symmetry.

Notice that this category of symmetry (reﬂection through the origin) does not guarantee

= 0, by the argument of Figure 4.6, since symmetric points have equal and opposite

values of both x and y coordinates, resulting in contributions to I

of the same sign.

228 4 Unsymmetrical Bending

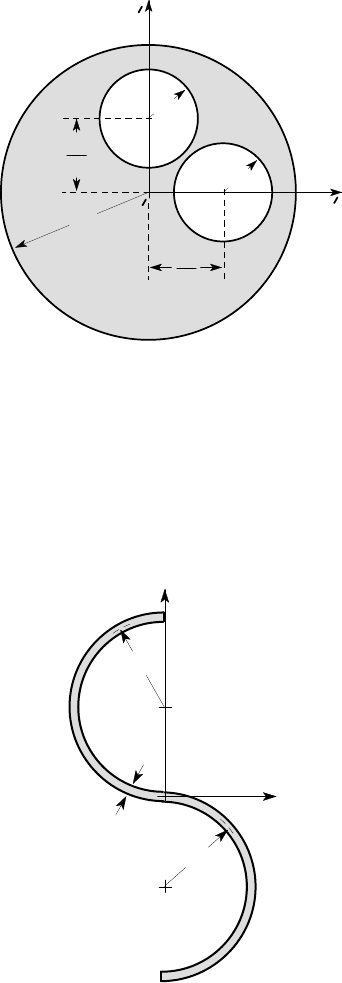
4.18. A beam of circular cross section, radius 3a has two eccentric circular holes of

radius a as shown in Figure P4.18.

Figure P4.18

Find the centroid of the section and the second moments of area I

about

centroidal axes.

Section 4.3.3

4.19.* Calculate I

for the S-section of Figure P4.19, using the ‘t ≪a’ approx-

imation. Note: You will need to use the integration method of Appendix B.

Figure P4.19

Problems 229

4.20. Calculate I

for the section of Figure 4.15, using the ‘t ≪a’ approxima-

tion and describing the section by the mean line. Which of the three second moments

is the most in error by this method and by what percentage?

4.21. A beam of the section shown in Figure P4.21 is loaded by a bending moment

about the y-axis. Calculate I

using the ‘t ≪a’ approximation and hence

determine the inclination of the neutral axis.

all thicknesses = t

Figure P4.21

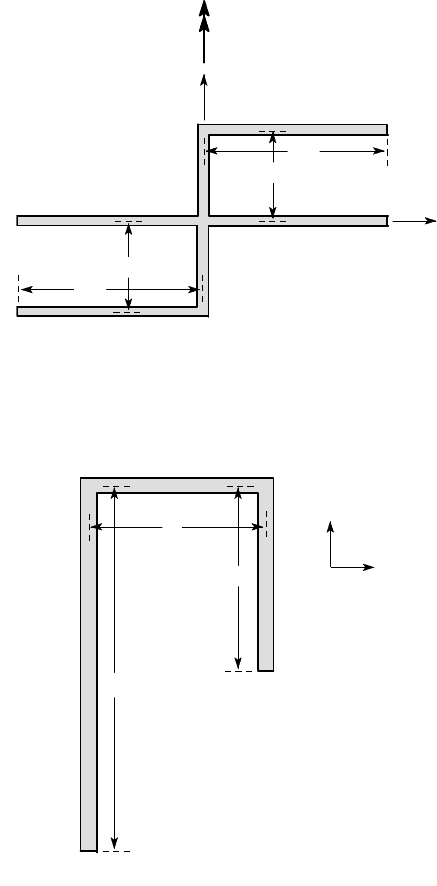
4.22. Find the location of the centroid and the second moments of area I

for

the thin-walled section of Figure P4.22.

all thicknesses = t

Figure P4.22

230 4 Unsymmetrical Bending

4.23. Find the location of the centroid and the second moments of area I

for

the section of Figure P4.23.

1.6

all dimensions in mm.

Figure P4.23

Section 4.4

4.24. For the cross section of Figure P4.21, with a = 20 mm, t = 3 mm, we obtain

=160×10

, I

=256×10

, I

=96×10

. Sketch the Mohr’s circle

of second moments of area and hence determine the magnitudes of the principal

second moments and the inclination of the principal axes to the x and y axes. Draw

in the principal axes on a copy of the ﬁgure and identify the stiff and ﬂexible axes as

‘1’, ‘2’, respectively.

4.25. Sketch Mohr’s circle of second moments of area for the section of Figure P4.6,

using the results for I

given in problem 4.6. Hence determine the magnitudes

of the principal second moments and the inclination of the principal axes to the x and

y axes. Draw in the principal axes on a copy of the ﬁgure and identify the stiff and

ﬂexible axes as ‘1’, ‘2’, respectively.

4.26. Sketch Mohr’s circle for second moments of area for the section of Figure P4.8,

using the results for I

given in problem 4.8. Hence determine the magnitudes

of the principal second moments and the inclination of the principal axes to the x and

y axes. Draw in the principal axes on a copy of the ﬁgure and identify the stiff and

ﬂexible axes as ‘1’, ‘2’, respectively.

4.27. Using the results for I

given in problem 4.9, determine the magnitudes of

the principal second moments and the inclination of the principal axes for the section

of Figure P4.9. Draw in the principal axes on a copy of the ﬁgure and identify the

stiff and ﬂexible axes as ‘1’, ‘2’, respectively.

4.28. The second moments of area for the section of Figure P4.28 are

= 26a

t ; I

40a

; I

= −14a

t .

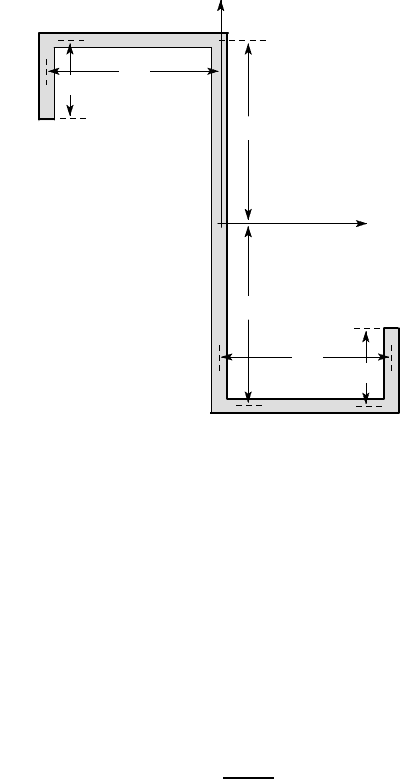
Problems 231

all thicknesses = t

Figure P4.28

Find the principal second moments of area and the inclination of the principal

axes. Draw in the principal axes on a copy of the ﬁgure and identify the stiff and

ﬂexible axes as ‘1’, ‘2’, respectively.

4.29*. A beam with second moments of area I

is loaded by a bending moment,

about the x-axis. Find an expression for the angle

between the resulting neutral

axis and the x-axis.

Devise a geometrical construction for the angle

on the Mohr’s circle of Figure

4.21 and hence show that for a given section, the maximum deviation between the

moment axis and the neutral axis is

max

= sin

−1



−I

+ I



Find the angle between the moment axis and the stiff axis (1) for this maximum

deviation to occur.

Section 4.4.3

4.30. Figure P4.30 shows the cross section of an unequal angle beam for which the

principal second moments of area are I

= 23.95×10

, I

= 2.53×10

The location of the centroid and the inclination of the principal axes are as shown.

The beam is subjected to a bending moment of 10 kNm about the x-axis. Find the

location and magnitude of the maximum tensile and compressive stress.

232 4 Unsymmetrical Bending

100

200

24.3

14.34

74.3

all dimensions in mm.

Figure P4.30

4.31. The beam of Problem 4.30 is subjected to a bending moment of 6 kNm about

the y-axis. Find the location and magnitude of the maximum tensile and compressive

stress.

4.32. The unequal Z-section of Figure 4.17 (a) has principal second moments I

5.255a

t,I

=0.761a

t and the inclination of the principal axes are as shown in Fig-

ure 4.23. The beam is loaded by a bending moment M

about the x-axis. Find the

location and magnitude of the maximum tensile stress.

Section 4.4.4

4.33. Make a copy of the three beam sections in Figure P4.33 and use the ‘least

squares ﬁt’ method to estimate the location of the principal axes on each section.

Label the stiff and ﬂexible axes ‘1’ and ‘2’ respectively.

(a) (b) (c)

Figure P4.33

Problems 233

4.34. Make a copy of the beam section of Figure P4.17 and use the ‘least squares ﬁt’

method to estimate the location of the principal axes on each section. Label the stiff

and ﬂexible axes ‘1’ and ‘2’ respectively.

4.35. Make a copy of the beam section of Figure 4.15 and use the ‘least squares ﬁt’

method to estimate the location of the principal axes on each section. Label the stiff

and ﬂexible axes ‘1’ and ‘2’ respectively.

4.36. Make a copy of the beam section of Figure P4.22 and use the ‘least squares ﬁt’

method to estimate the location of the principal axes on each section. Label the stiff

and ﬂexible axes ‘1’ and ‘2’ respectively.

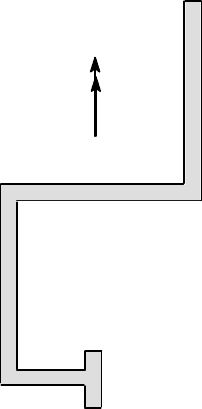
4.37. A beam with the cross section of Figure P4.37 is loaded by a bending moment

about the vertical axis as shown. Show on the ﬁgure your best estimate of (i) the

location of the principal axes, (ii) the location of the neutral axis and (iii) the point P

where the maximum tensile stress will occur.

Figure P4.37

4.38. A beam with the S-section of Figure P4.19 is loaded by a bending moment

about the x-axis. Show on the ﬁgure your best estimate of (i) the location of the

principal axes, (ii) the location of the neutral axis and (iii) the point P where the

maximum tensile stress will occur.

4.39. Estimate the location of the principal axes for the beam section of Figure P4.6

using the ‘least squares ﬁt’ method and hence ﬁnd the approximate location of the

234 4 Unsymmetrical Bending

neutral axis when the beam is loaded by a bending moment about the x-axis. If you

previously solved Problem 4.6, compare your estimate for the inclination of the neu-

tral axis with the exact calculation.

4.40. Estimate the location of the principal axes for the beam section of Figure P4.9

using the ‘least squares ﬁt’ method and hence ﬁnd the approximate location of the

neutral axis when the beam is loaded by a bending moment about the x-axis. If you

previously solved Problem 4.9, compare your estimate for the inclination of the neu-

tral axis with the exact calculation.

Section 4.4.5

4.41. The I-beam shown in Figure P4.41 is subjected to a bending moment which is

intended to be aligned with the axis Ox, but which is actually inclined at 1

towards

Oy because of a manufacturing error.

180

all dimensions in mm.

Figure P4.41

Find I

and hence the direction of the neutral axis, (which is also the axis about

which bending occurs).

4.42. An I-beam section is to be used for a cantilever beam to support an end load

whose direction may deviate from the vertical by ±0.5

due to manufacturing and

assembly errors. Determine the maximum permissible ratio I

if the horizontal

displacement is not to exceed 10% of the vertical displacement.