Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

5.5 Bending of a symmetric section about an orthogonal axis 255

c = ±

−d .

If d > 0, only the positive square root

gives a physically reasonable result. For

this case,

= 2S

−d

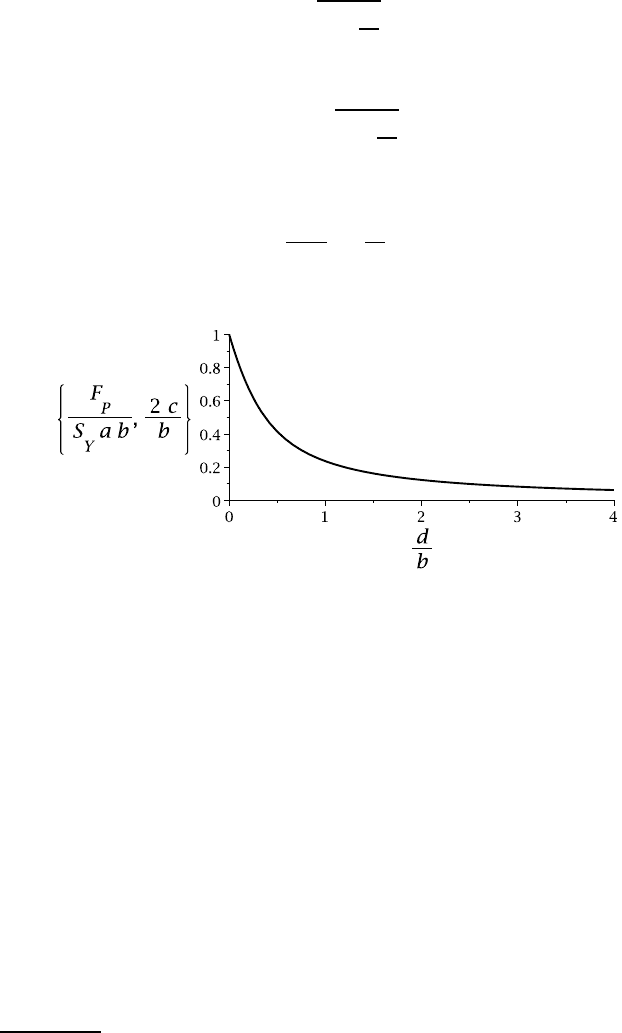
The dimensionless quantities

;

both vary with the load offset d as shown in Figure 5.17.

Figure 5.17

Notice that when d =0, there is no offset of the load and we obtain c=b/2, which

identiﬁes the neutral axis with the lower edge of the cross section. This simply means

that the whole section is above the neutral axis and hence is yielding in tension at

, leading to a collapse load, F

ab.

For any non-zero value of d, however small, c will be less than b/2 and there will

be a region of compressive stress below the neutral axis.

5.5.3 The partially plastic solution

The problem of determining the stress ﬁeld for applied moments between M

and

is rather more complicated. We ﬁrst note that the beam will remain elastic as

long as

=My/I <S

for all values of y, measured from the centroidal axis. When

this condition is violated, yield will start at the point in the section where |y| is a

maximum and this will generally be on one side of the axis only, since the section is

unsymmetrical. This plastic zone will grow with M until at some intermediate value

a second plastic zone initiates on the other side of the axis. Both zones then grow at

For d < 0, we would need to take the negative square root, but the solution would merely

be a mirror image of that given here.

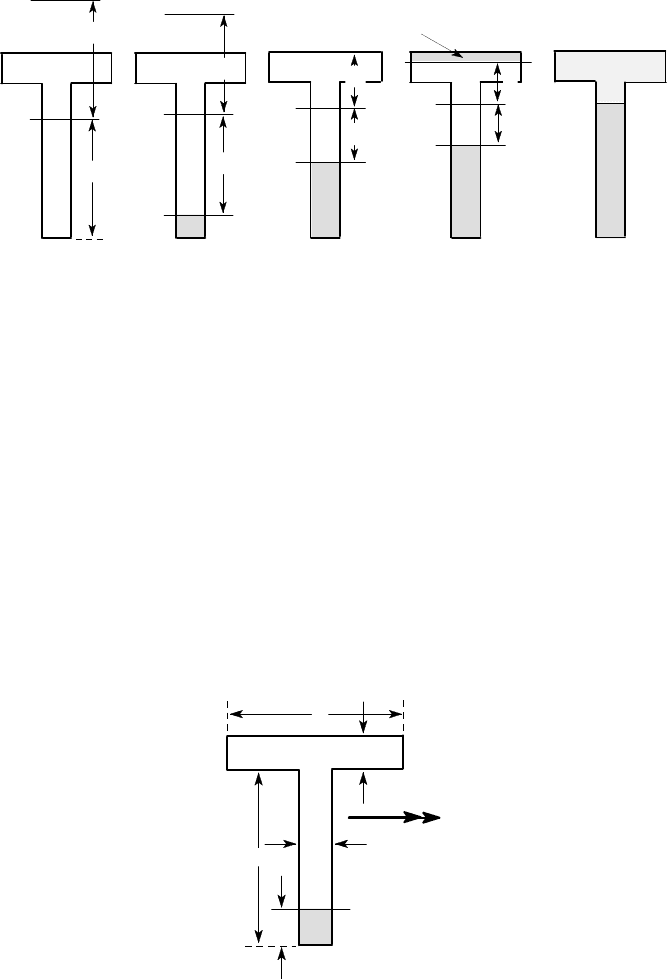
256 5 Non-linear and Elastic-Plastic Bending

the expense of the elastic zone until eventually the section becomes fully plastic at

-S

(a) (b) (c) (d) (e)

Figure 5.18: Development of plastic zones for a symmetric section bent about an

orthogonal axis: (a) ﬁrst yield, (b) one plastic zone, (c) initiation of yield at top of

section, (d) two plastic zones, (e) full plasticity

This process is illustrated by the sequence of Figures 5.18 (a–e). Notice how the

plastic zones develop and also how the neutral axis moves away from the centroid C

as the moment is increased. Throughout the process, the position of the neutral axis

and the dimension d are determined in terms of the force F and the moment M

using

the ﬁrst two of equations (5.16).

Example 5. 6

The T-beam of Figure 5.19 is loaded by a bending moment about the x-axis. Find an

equation relating the bending moment M and the dimension c deﬁning the extent of

the plastic zone for the case illustrated where there is only one plastic zone. Also,

ﬁnd the value of c at which a second plastic zone will start to develop at the top of

the section. The material yields at constant yield stress ±S

Figure 5.19

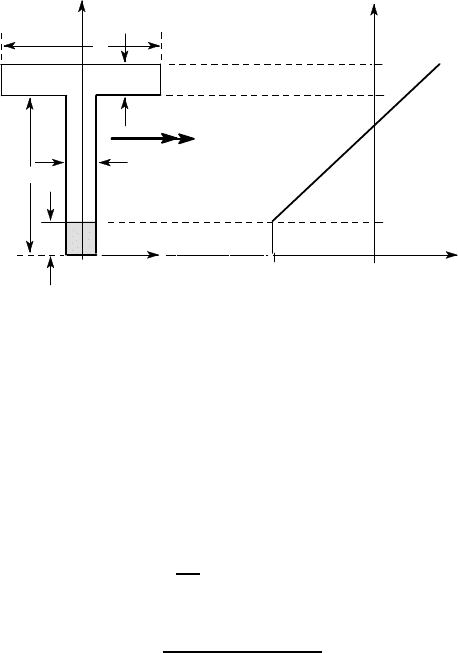
5.5 Bending of a symmetric section about an orthogonal axis 257

Since we don’t yet know the location of the neutral axis, it is convenient to take

the origin at the bottom of the section as shown in Figure 5.20 (a). The material has

yielded in compression (

= −S

) in 0 < y < c and the stress must vary linearly in

the elastic range as shown in Figure 5.20 (b). Thus

= −S

; 0 < y < c

= −S

+C(y −c) ; c < y < a + b ,

where C is a constant to be determined. Notice how the second expression satisﬁes

the condition that the stress in the elastic region just above y = c should be on the

point of yielding — in other words, the stress is a continuous function of y.

a+b

-S

(a) (b)

Figure 5.20

We can determine the value of C from the condition that the total axial force be

zero. From the ﬁrst of (5.16), we have

F =

dA = −S

bc +

[−S

+C(y −c)]bdy +

a+b

[−S

+C(y −c)]ady .

Performing the integrals and simplifying, we ﬁnd

F = −2abS

(3a

+ ab + c

−4ac) = 0

and hence

C =

4aS

+ ab + c

−4ac

The neutral axis corresponds to the point y= y

, where

=0 and hence

−S

+C(y

−c) = 0 .

Solving for y

and using the above value of C, we obtain

258 5 Non-linear and Elastic-Plastic Bending

= c +

+ ab + c

−4ac

+ ab + c

The moment corresponding to this stress distribution can be found by taking

moments about any convenient horizontal axis, since there is no axial force F. Thus,

using the axis y= 0 of Figure 5.20 (a), we have

M =

ydA =

(−S

)ybdy +

[−S

+C(y −c)]bydy

a+b

[−S

+C(y −c)]aydy .

After performing the integrals and substituting for C, we ﬁnd

M =

ab(5a

+ 6a

b + 12a

c + 5ab

−9ac

−3bc

+ 4c

−12abc)

6(3a

+ ab + c

−4ac)

This is the required relation between M and c.

The second plastic zone will start when

at y =a + b — i.e.

−S

+C(a + b −c) = S

Substituting for C and simplifying, we obtain

−ab + c

−2ac = 0 ,

with solution

c = a ±

−(a

−ab) = a ±

√

ab .

Only the negative square root makes sense here, so yield at the top of the section

starts when

c = a −

√

ab .

It is clear from this example that the process is algebraically very complicated,

even for a relatively simple beam section. The second stage of the process, where

there are two plastic zones is equally complicated. The chances of making an al-

gebraic error in such calculations is so large that they are only really practicable

if performed symbolically using a language such as Mathematica or Maple or im-

plemented numerically. Fortunately most of the important information for design

against failure can be extracted from the limiting cases of ﬁrst yield and full plas-

ticity, which we have seen are easier to compute. The exception is the problem of

residual stress and springback, which we discuss in §5.7 below and which unfortu-

nately requires a solution for the stress ﬁeld at the maximum applied load.

5.6 Unsymmetrical plastic bending

If the beam section has no axis of symmetry or if the bending moment is applied

about an inclined axis, the problem is even more complicated and generally neces-

sitates a numerical solution. However, the limiting solutions for ﬁrst yield and full

plasticity are still approachable algebraically.

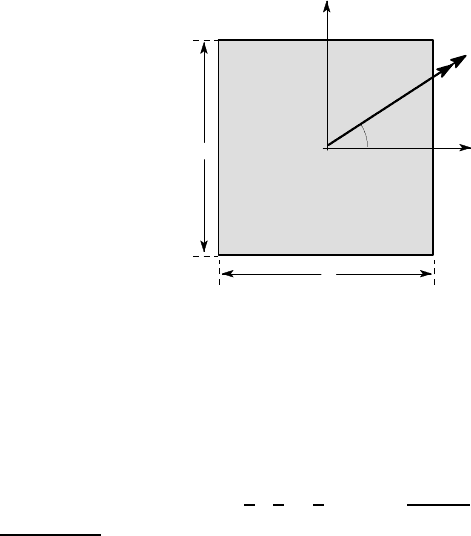
5.6 Unsymmetrical plastic bending 259

For ﬁrst yield, we perform an elastic analysis, using the techniques of Chapter

4. After ﬁnding the location and magnitude of the maximum stress

max

, the yield

moment M

can then be determined by equating

max

to ±S

as appropriate.

For full plasticity, we know that the neutral axis will divide the section into two

equal areas of tensile and compressive yield respectively, if there is no axial force.

Because of the lack of symmetry, we do not know the inclination of the neutral axis,

but we can obtain an equation to determine it by requiring that the resultant plastic

moment be about the speciﬁed bending axis. One way to implement this condition

is to take moments about an axis perpendicular to the applied moment axis and set

the resultant to zero. This procedure leads to manageable algebraic calculations for

thin-walled sections and for some other simple geometries.

Example 5. 7

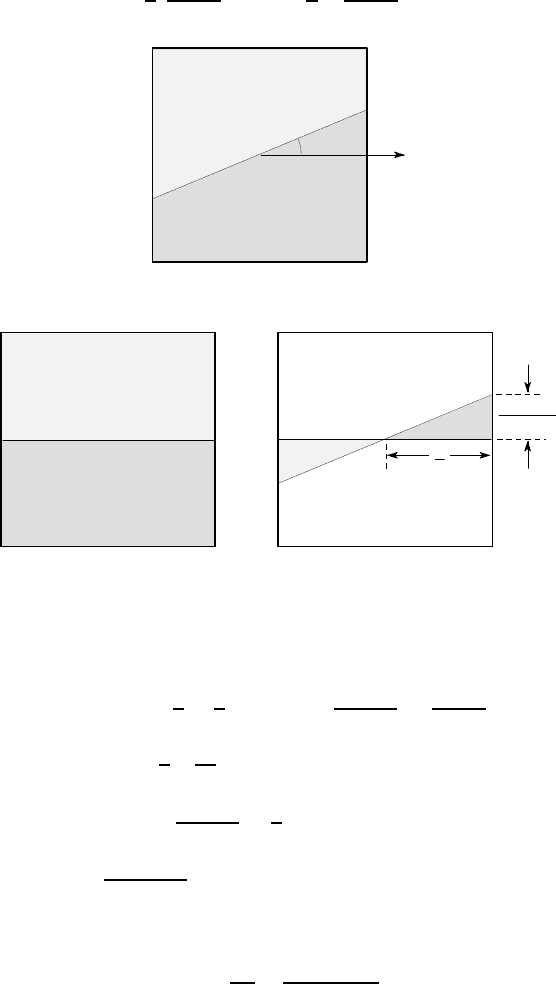
A beam of square cross section a×a is subjected to a bending moment about an axis

inclined at an angle

to the horizontal, as shown in Figure 5.21. The moment is

sufﬁcient to cause plastic collapse of the section. Assuming that the neutral axis is

inclined at an angle

to the horizontal, ﬁnd the relation between

and

in the

range −

/4 <

/4 and the corresponding value of the fully plastic moment M

Figure 5.21

The inclined neutral axis must pass through the centre of the square, since any

such line divides the section into two equal areas. If the axis is inclined at an angle

, the stress at plastic collapse will be as shown in Figure 5.22 (a).

For the purposes of calculation, it is convenient to consider this as the sum

of the

distributions of Figure 5.22 (b,c). The area of each of the triangles in Figure 5.22 (c)





tan



tan

Notice that this superposition is valid as long as we only use it to calculate force and

moment resultants, but the deformations due to the stress ﬁelds of Figure 5.22 (b,c) do not

generally sum to those due to Figure 5.22 (a), since the constitutive law is non-linear.

260 5 Non-linear and Elastic-Plastic Bending

and their centroids are at the points



a tan



;



−

,−

a tan



-S

(a)

-S

-2S

a tan α

(b) (c)

Figure 5.22

We can therefore compute the moments about the x and y axes as

= 2S

(a)







−2(2S

)



tan



a tan



= a



−

tan



= 2(2S

)



tan







tan

The angle of inclination of the applied moment axis can then be written

tan

2tan

(3 −tan

)

5.6 Unsymmetrical plastic bending 261

with solution

tan

√

1 + 3 tan

−1

tan

This is the required relation between

and

. It is valid only in the range −

/4 <

<−

/4, since beyond this range the neutral axis will intersect the top and bottom

of the section rather than the sides. However, the same result can be extended into

other ranges by rotating the ﬁgure through 90

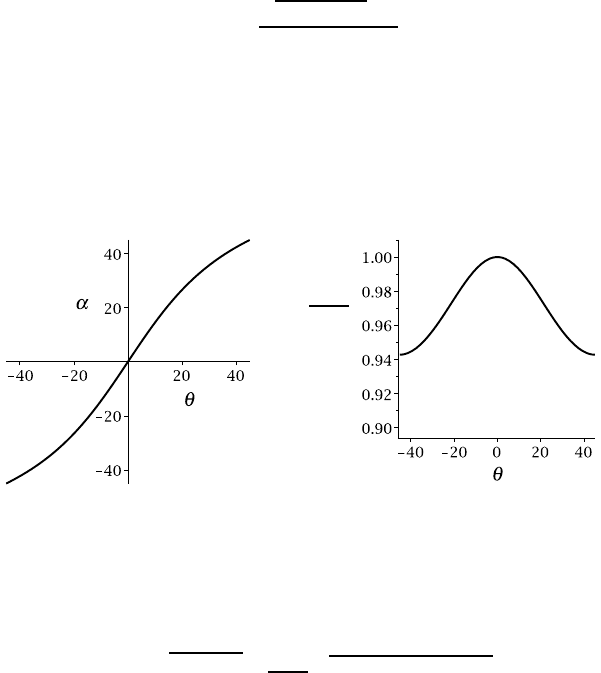
The variation of

with

(in degrees) is illustrated in Figure 5.23 (a). Notice that

=−

/4, 0,

/4 etc. due to symmetry.

(a) (b)

Figure 5.23

The resultant fully plastic moment is

+ M

9 −2 tan

+ tan

This expression is shown in Figure 5.23 (b). The moment M

varies between a max-

imum of 0.25a

=0 and a minimum of 0.236a

=±

/4.

Example 5. 8

The thin-walled unsymmetrical U-section of Figure 5.24 is loaded by a moment about

the horizontal axis. Find the fully plastic moment M

and the inclination of the cor-

responding neutral axis.

There is no axial force and hence the areas above and below the neutral axis must

be equal, giving

(a −d

) + (2a −d

) = d

+ a + d

— i.e.

2(d

+ d

) = 2a .

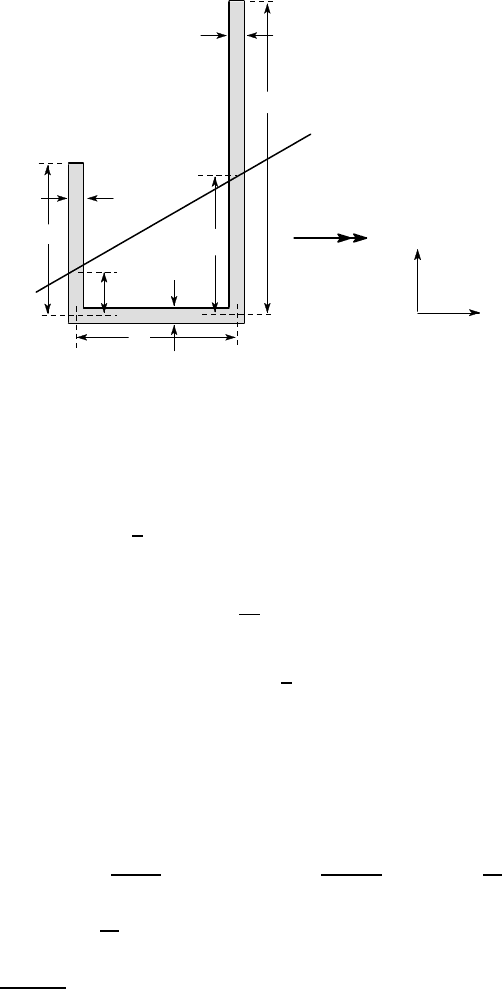
262 5 Non-linear and Elastic-Plastic Bending

neutral

axis

Figure 5.24

Since the moment is applied about the x-axis, the component M

must be zero.

It is convenient to enforce this condition by taking moments about a vertical axis

through the point B in Figure 5.24, since then the forces acting on AE and EB have

zero moment arm and make no contribution. We obtain

−S

(at)

−S

t)a + S

(2a −d

)ta = 0

— i.e.

We can then recover d

= a −d

This completes the solution for the neutral axis and shows that the horizontal

bending moment causes the beam to bend about an axis that is inclined at an angle of

tan

−1

(0.5) to the horizontal. The neutral axis also completely deﬁnes the stress ﬁeld

at full yield and the plastic moment can therefore be obtained by taking moments

about the horizontal axis passing through BC, giving

= S

(a −d



a + d



+ S

(2a −d



2a + d



−S





−S





15S

after substituting for d

5.7 Unloading, springback and residual stress 263

5.7 Unloading, springback and residual stress

If a beam is loaded into the plastic range and then unloaded, there will be some

permanent residual curvature and the material will be left in a state of residual stress.

We ﬁrst note that the argument of §5.1 remains valid during the unloading process,

so the strain is at all times a linear function of position in the section. As we start

to reduce the bending moment, the magnitude of the strain will decrease and those

parts of the cross section that have yielded will unload along a parallel elastic line

such as CD in Figures 5.2, 5.3. In most cases, the unloading process is completely

elastic (i.e. no further yield occurs as the bending moment is reduced to zero) and

hence the change in the stress ﬁeld during unloading is identical to that produced in

a corresponding elastic beam subjected to the same change of bending moment.

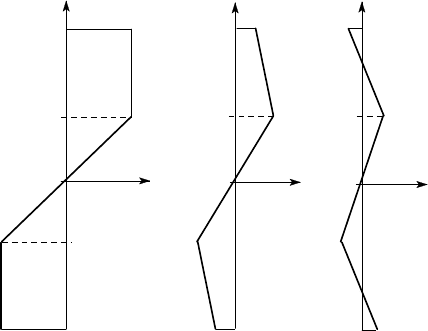
Figure 5.25 shows the evolution of the stress distribution for a symmetric beam

bent about an axis of symmetry. We suppose the maximum bending moment M

max

lies in the range M

< M

max

< M

, so that the corresponding stress distribution has

the form of Figure 5.25 (a), with plastic zones at the top and bottom of the beam,

separated by a central elastic region of depth 2d. As the moment is reduced, the

strain and hence the stress reduces by an amount proportional to the distance from

the neutral axis, leading to a stress distribution of the form of Figure 5.25 (b). If

the moment is completely removed, the stress distribution must have zero resultant

moment and hence must have regions of tensile and compressive stress on each side

of the neutral axis, as shown in Figure 5.25 (c).

-S

-d

(a) (b) (c)

Figure 5.25: Evolution of the stress distribution during loading and unloading: (a)

maximum load, (b) partial unloading, (c) complete unloading

In algebraic terms, the stress ﬁeld at M

max

(Figure 5.25 (a)) can be written

= S

; y > d (5.29)

264 5 Non-linear and Elastic-Plastic Bending

; −d < y < d (5.30)

= −S

; y < −d (5.31)

and that for any stage of elastic unloading is

= S

−

∗

; y > d (5.32)



−

∗



y ; −d < y < d (5.33)

= −S

−

∗

; y < −d , (5.34)

where M

∗

= M

max

−M is the reduction in bending moment from the elastic-plastic

state described by equations (5.29–5.31). In the special case of complete unload-

ing [Figure 5.25 (c)], where we reduce the applied moment to zero, M

∗

= M

max

and

hence the residual stress ﬁeld is the difference between that which is obtained by

elastic-plastic analysis at M

max

and that which would have been obtained at the same

moment (M

max

), if the material had had a sufﬁciently high yield stress to remain

elastic. Students sometimes have difﬁculty with this concept, arguing that if the su-

perposed stress ﬁeld due to M

∗

is one that could not have been applied to the original

beam without causing yield, then some yielding should occur on unloading. How-

ever, yielding is governed by the instantaneous value of stress — not by its change

from some previous value. Indeed, in the uniaxial stress-strain curve of Figure 5.3,

the stress can be reduced by 2S

from point C before yielding occurs at F, whereas

an unstressed bar could only experience a change of S

without yielding. For the

bending problem, as long as the stress deﬁned by equations (5.32–5.34) remains in

the range −S

< S

at all points for 0 < M

∗

< M

max

, the unloading process

will remain elastic. This is always the case when bending occurs about an axis of

symmetry.

An exactly similar process of superposition can be used for beams which are

not bent about an axis of symmetry. In other words, we ﬁrst solve the elastic-plastic

problem as in §§5.5, 5.6 to establish the stress ﬁeld under the maximum bending

moment and then subtract the solution of an equivalent elastic problem to obtain

the residual stress. Notice however that in this case, the neutral axis for the two

superposed stress ﬁelds will be different. If the maximum bending moment is at or

near to M

, this can cause a small amount of additional yielding to occur near the

neutral axis during unloading.

5.7.1 Springback and residual curvature

During unloading, the curvature is reduced and the magnitude of this change is given

by the beam bending equation as

∗

. (5.35)