Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

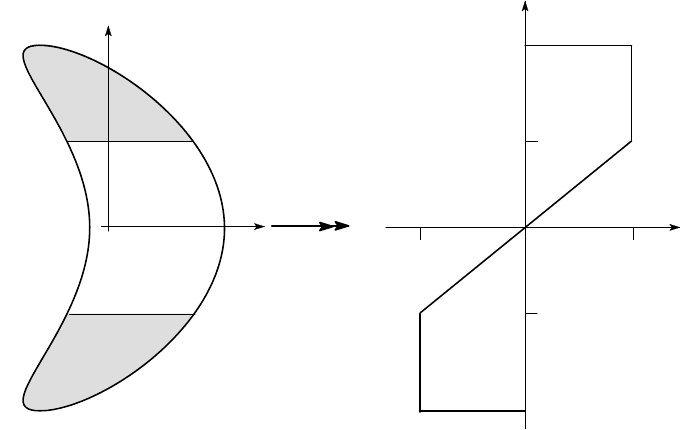
5.4 Pure bending about an axis of symmetry 245

Some simpliﬁcation follows from the fact that the stress is uniform in each plastic

region, permitting the stress distribution there to be replaced by a force resultant

through the local centroid. Figure 5.6 shows (a) a representative symmetric section

and (b) the corresponding stress distribution when the beam is loaded into the plastic

r´egime.

If the beam is bent to a radius R, the dimension d is given by equation (5.15).

The resultant bending moment can be written symbolically in the form

M = M

+ M

≡

ydA +

ydA , (5.19)

where A

are the areas of the two plastic regions and the elastic region respec-

tively, as shown in Figure 5.6 (a).

-d

(a) (b)

Figure 5.6: Bending about an axis of symmetry: (a) elastic and plastic zones, (b) the

corresponding stress distribution

In A

, the stress is uniform and equal to S

, so

= S

ydA = S

¯y

, (5.20)

where ¯y

is the coordinate of the centroid of A

. Similarly, in A

=−S

, leading

= −S

¯y

, (5.21)

but since the beam is symmetrical and loaded symmetrically, ¯y

= −¯y

, and hence

and M

+ M

=2M

246 5 Non-linear and Elastic-Plastic Bending

These results have a simple physical explanation. The stress is uniform over A

and hence the resultant is a force of magnitude S

acting through the centroid of

. As in §4.3.1, the value of A

¯y

for composite areas can conveniently be written

as the sum of similar results for the component areas.

Turning now to the elastic region A

, the expression for M

[the third integral in

equation (5.19)] is exactly the same as the moment transmitted by an elastic beam of

cross section A

bent to a radius R — i.e.

, (5.22)

where I

is the second moment of area of the ‘embedded elastic beam’ of cross

section A

. Thus, the total moment can be written

M =

+ 2S

¯y

(5.23)

= S



+ 2A

¯y



, (5.24)

using (5.15), where we recall that d is the distance from the neutral axis to the start

of the plastic region.

Example 5. 2

The I-beam of Figure 5.7 is loaded by a monotonically increasing bending moment

M. Find the relation between M and the radius of curvature R if the material is

elastic-perfectly plastic with Young’s modulus E =210 GPa and yield stress S

=400

MPa.

200

100

all dimensions in mm

Figure 5.7

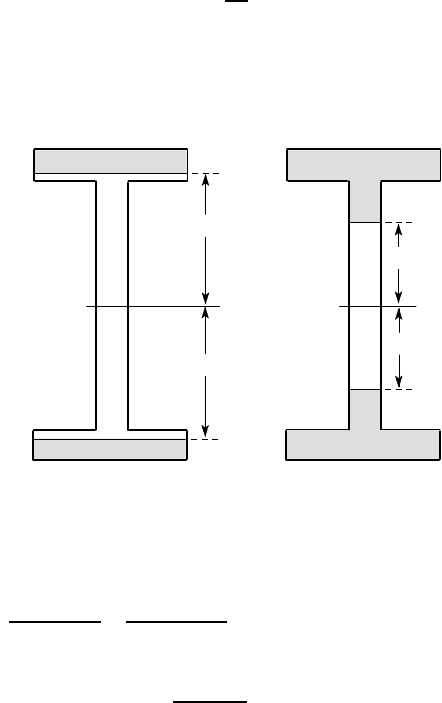
5.4 Pure bending about an axis of symmetry 247

For low values of M, the beam will be entirely elastic and the relation between

M and R is given by the elementary equation

M =

where I is the second moment of area for the entire section, which we determine

below.

After plastic deformation begins, we can distinguish the two qualitatively differ-

ent states shown in Figures 5.8 (a,b).

(a) (b)

Figure 5.8

For case (a), the second moment of area I

for the embedded elastic beam is

(2d)

×0.1

−

0.16

×0.08

= 0.0667d

−27.3 ×10

−6

and

¯y

= 0.1 ×(0.1 −d) ×

(0.1 + d)

= 0.5 ×10

−3

−0.05d

The value of I for the full section, which we need to describe the solution in the

elastic range, is obtained by setting d = 0.1 m in the expression for I

above — i.e.

I = 0.0667 ×(0.1)

−27.3 ×10

−6

= 39.4 ×10

−6

Substituting for I

, A

¯y

in (5.24), we have

M = S

(0.0667d

−27.3 ×10

−6

−1

+ 10

−3

−0.1d

)

= 400 ×10

(10

−3

−0.0333d

−27.3 ×10

−6

−1

) Nm.

In particular, ﬁrst yield corresponds to the value d =0.1 and hence

248 5 Non-linear and Elastic-Plastic Bending

= 157,600 Nm = 157.6 kNm.

The relation between M and R is obtained by substituting

d =

= 1.90 ×10

−3

and hence

M = 400 ×10

(10

−3

−0.121 ×10

−6

−14.33 ×10

−3

−1

) Nm.

We also note that the radius of curvature at ﬁrst yield is

0.1E

= 52.5 m,

from (5.15).

Case (a) applies as long as 0.08 < d < 0.1 and hence the transition to case (b)

occurs when

M = 400 ×10

(10

−3

−0.0333 ×0.08

−27.3 ×10

−6

0.08

−1

) = 178100 Nm.

For case (b),

(2d)

×0.02

= 0.01333d

and

¯y

= 0.1 ×0.02 ×0.09 + (0.08 −d) ×0.02 ×

(0.08 + d)

= 0.244 ×10

−3

−0.01d

where we have treated the ﬂange and the section of web above y=d as two separate

areas for this computation.

Thus, using equation (5.24),

M = S

(0.01333d

+ 0.488 ×10

−3

−0.02d

= 400 ×10

(0.488 ×10

−3

−6.67 ×10

−3

) Nm

= 400 ×10

(0.488 ×10

−3

−24 ×10

−9

) Nm.

The maximum bending moment M

occurs when d = 0,R = 0 and the section is

fully plastic. We therefore have

= 400 ×10

×0.488 ×10

−3

= 195,200 Nm = 195.2 kNm.

The relation between M and R is illustrated in Figure 5.9.

5.4 Pure bending about an axis of symmetry 249

0.0190

0.0238

195.2

178.1

157.6

kNm

(a)

(b)

(m )

-1

elastic

Figure 5.9

5.4.2 Fully plastic moment and shape factor

In the above example, Figure 5.9 shows that the curvature increases rapidly once we

exceed the moment M

for ﬁrst yield and in fact the fully plastic moment M

is not

very much larger than M

. We deﬁne the shape factor

f =

(5.25)

and for the I-beam of the example we have f =195.2/157.6=1.239. In other words, a

24% increase in moment beyond ﬁrst yield is sufﬁcient to cause the beam to collapse

completely. I-beams in general have relatively low values of shape factor because

the ﬂanges are responsible for the greater part of the moment transmitted in bending

and the ﬂange stresses are nowhere much below the yield stress when the outermost

ﬁbres yield.

From a design point of view, it is often sufﬁcient to determine just M

and M

since these deﬁne respectively the moment above which some permanent damage

can be expected and the moment for total collapse of the beam. For the fully plastic

case, equation (5.24) reduces to

= 2S

A ¯y , (5.26)

where A is the area above the axis of symmetry and ¯y is the coordinate of its centroid.

Example 5. 3

Determine M

and the shape factor f for a solid circular section of diameter d,

if the uniaxial yield stress for the material is S

First yield will occur when the stress at y=d/2 is equal to S

, so

250 5 Non-linear and Elastic-Plastic Bending

giving

where we have used the result that I =

/64 for a circular cross section of diameter

For the fully plastic case, we have

A ¯y =

ydA =

d/2

r sin

rdrd





for the area above the axis of symmetry, using the integration scheme of Figure 5.10.

dA = r dr dθ

y = r sin θ

dθ

Figure 5.10

It then follows that

= 2S





and the shape factor is

f =

= 1.70 .

Notice that the shape factor is larger for the circle than for the I-beam, because the

greater volume of material nearer to the axis of symmetry contributes signiﬁcantly

to the transmitted moment.

5.5 Bending of a symmetric section about an orthogonal axis

Figure 5.11 shows a beam section which is symmetric about the y-axis, but which is

bent about the x-axis.

Suppose that the neutral axis is parallel to the x-axis, so that the strain and hence

the stress is a function of y only. It then follows from the third of equations (5.16)

that M

= 0, since symmetric elements with equal and opposite values of x cancel

each other in the integral. We therefore deduce that the neutral axis will be parallel

to the bending axis, when this is orthogonal to an axis of symmetry for the section.

5.5 Bending of a symmetric section about an orthogonal axis 251

Figure 5.11: Symmetric section bent about an orthogonal axis

This argument is not subject to the other restrictions listed in §5.4 — in particular,

it applies if there is an axial force and also if the monotonic stress-strain relation is

different in tension and compression. However, the neutral axis will not generally

pass through the centroid of the section and it will move (whilst remaining parallel

to the bending axis) as the loading increases.

5.5.1 The fully plastic case

The simplest case is that of full plasticity, where every point in the section has yielded

and is either at S

or −S

as shown in Figure 5.12.

Figure 5.12: Fully plastic state for bending of a symmetric section about an orthog-

onal axis

The axial force is then

F =

dA =

dA +

(−S

)dA = (A

−A

, (5.27)

where A

are the areas above and below the neutral axis respectively. If there is

no axial force, F =0 and A

= A

. In other words, the neutral axis for full plasticity

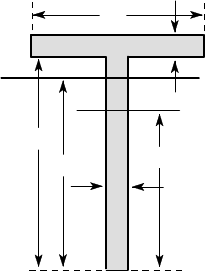
252 5 Non-linear and Elastic-Plastic Bending

divides the section into two equal areas. For sections that are not symmetric about the

x-axis, this ‘median line’ does not generally pass through the centroid. For example,

the centroid of the T-section of Figure 5.13 is 74.4 mm from the bottom, whereas

the median line is 90 mm from the bottom. Thus, if we apply a gradually increasing

bending moment M to the T-section beam, the neutral axis will initially pass through

the centroid, but it will migrate upwards after yielding starts, tending towards the

median line as the fully plastic moment M

is approached.

100

median

centroidal axis

74.4

all dimensions in mm

Figure 5.13: Centroidal and median axes for a T-section

Once the neutral axis has been found, the fully plastic moment is determined as

ydA +

(−S

)ydA = S

¯y

−A

¯y

) , (5.28)

where ¯y

, ¯y

deﬁne the centroids of the areas A

. Since there is no axial force, any

convenient origin may be used to deﬁne the coordinates ¯y

, ¯y

Example 5. 4

Find the fully plastic moment for the U-section of Figure 5.14, if the material yields

at a stress S

=300 MPa.

The total area of the section is

A = 100 ×100 −80 ×60 = 5200 mm

so the area above the median line must be A/2 = 2600 mm

. The neutral axis is

therefore 65 mm from the top of the section (since 65 ×40 = 2600) as shown in

Figure 5.15.

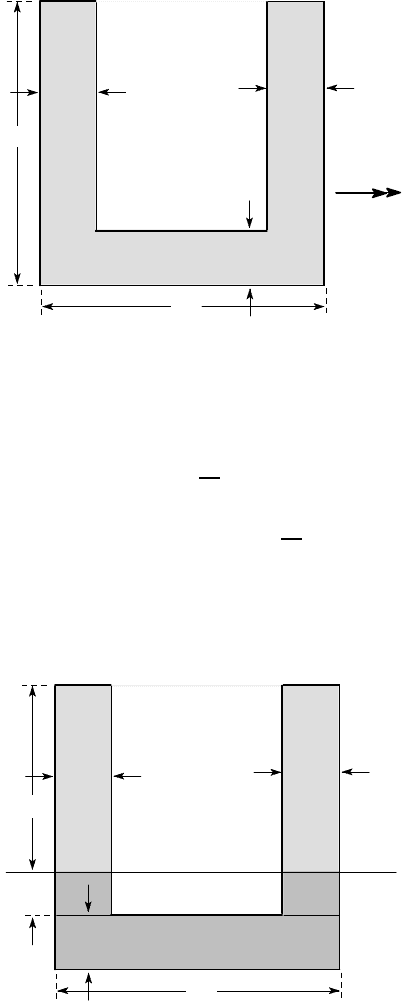
5.5 Bending of a symmetric section about an orthogonal axis 253

100

all dimensions in mm

Figure 5.14

We therefore have

¯y

= 65 ×40 ×

= 84,500 mm

¯y

= 20 ×100 ×(−25) + 15 ×40 ×



−



= −54,500 mm

and

= 300 ×10

(84500 + 54500) ×10

−9

= 41,700 Nm,

from equation (5.28).

100

neutral axis

all dimensions in mm

Figure 5.15

254 5 Non-linear and Elastic-Plastic Bending

5.5.2 Non-zero axial force

The method is only slightly modiﬁed if the axial force is non-zero. Equation (5.27)

again provides a condition for determining the location of the neutral axis after which

the fully plastic moment is given by (5.28). Notice however that if there is an axial

force, the resultant moment will depend on the axis about which it is computed. An

alternative description of the loading in such cases is to specify the resultant axial

force and its line of action.

Example 5. 5

A rectangular beam of width a and depth b is loaded by an axial tensile force F

whose line of action is displaced a distance d from the axis of symmetry, as shown

in Figue 5.16. Find the collapse load F

and the dimension c deﬁning the location of

the neutral axis and sketch their variation with d.

b / 2

neutral axis

b / 2

(a) (b)

Figure 5.16

At collapse, the section above the neutral axis has yielded in tension and that

below in compression, so the axial force is obtained from (5.27) as

= S



+ c



−S



−c



= 2S

ac .

The moment about the axis of symmetry is

M = F

d = S



+ c





−c



−S



−c





−

−c



= S



−c



Substituting for F

and cancelling a factor S

, we have

−c

= 2cd ,

with solution