Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

Non-linear and Elastic-Plastic Bending

In this chapter, we shall consider the question of determining the stress distribution

and curvature when a beam is subjected to bending moments sufﬁcient to cause plas-

tic deformation. The same analytical procedure can also be used for the bending of

beams made of materials such as rubber, which have a non-linear elastic constitutive

behaviour.

Engineering components are generally not expected to experience plastic defor-

mation in normal service, but a calculation of the maximum load that can be carried

in a single exceptional loading experience is often of interest from a safety viewpoint.

A dramatic example is provided by studies of the crash behaviour of automobiles,

which are based on elastic-plastic analysis of the structural elements of the vehicle.

We shall also ﬁnd that when a beam is loaded into the plastic range and then

released, it does not return to its original conﬁguration and there are generally resid-

ual stresses remaining. This information forms the basis of analyses of simple metal

forming processes, such as the forming of a curved bar by plastic bending of a bar

that is initially straight.

5.1 Kinematics of bending

In the elementary theory of bending, it is customary to assume that initially plane

sections remain plane. This assumption seems plausible, but the background to it is

seldom discussed in any detail.

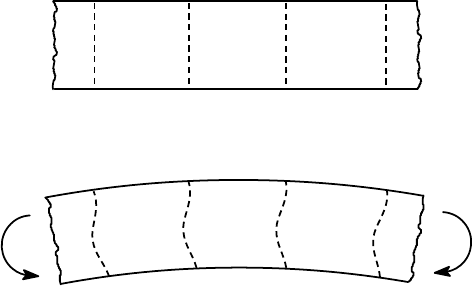
To ﬁx ideas, suppose we have a very long beam, subjected to pure bending by the

application of equal and opposite moments at the end. We imagine the beam as made

up of a large number of identical slices, with initially parallel plane faces, as shown

in Figure 5.1 (a). The stress distribution near the ends of the beam will be affected

by the precise way in which the moment is applied — i.e. by the traction distribution

on the two end faces, but it is reasonable to assume that this end effect will decay

as we get further from the ends and that there is some ‘preferred’ way in which the

moment will be transmitted along the beam. This idea is known as Saint-Venant’s

J.R. Barber, Intermediate Mechanics of Materials, Solid Mechanics and Its Applications 175,

2nd ed., DOI 10.1007/978-94-007-0295-0_5, © Springer Science+Business Media B.V. 2011

236 5 Non-linear and Elastic-Plastic Bending

principle. Thus, sufﬁciently far from the ends of the beam, the stress distribution on

all cross-sectional planes will be the same.

(a)

(b)

Figure 5.1: Deformation of the beam: (a) the undeformed conﬁguration; (b) after

deformation

In particular, the stress distribution across AB in Figure 5.1 (a) will be the same

as that across CD and EF. It follows that the element ABCD is loaded in exactly the

same way as the element CDEF and hence the deformed shapes of the two elements

must be the same. This implies that the deformed shape of the initially straight line

AB must be the same as that of CD.

Now the deformation of the elements must be one which preserves compatibil-

ity — in other words, adjacent slices must still be capable of stacking against each

other without generating any gaps. We illustrate this in Figure 5.1 (b). Each of the

initially straight vertical lines must deform to the same shape and the most general

deformation permitted in the beam is one in which (for example) AB deforms to an

arbitrary new shape and CD deforms to the same shape, but with an arbitrary (small)

rigid-body translation and rotation. The translation of CD to the right relative to AB

will lead to a uniform tensile strain across the element ABCD and the rotation will

lead to a tensile strain that varies linearly with y, regardless of the common deformed

shape of AB and CD. To convince yourself of this, draw an arbitrary curve on a sheet

of paper, copy the same curve onto a transparent sheet and experiment with various

small rigid body displacements of one curve with respect to the other. You will ﬁnd

that the most general change in the distances between corresponding points on the

curves due to the relative motion is a general linear function of y and furthermore,

that the multiplier on y is proportional to the rigid-body relative rotation of the two

curves in radians.

Similar considerations apply to the more general three-dimensional case and lead

to the conclusion that regardless of the common deformed shape adopted by the var-

ious initially plane sections, the axial strain e

must be a linear function of position

5.2 Elastic-plastic constitutive behaviour 237

in the section — i.e.

= C

x +C

y , (5.1)

where C

are unknown constants. This is all that is necessary to establish the

bending theory. It is not necessary to make the more restrictive assumption that plane

sections remain plane. To verify this, go back and review §4.1. You will ﬁnd that we

only used the assumption to arrive at equation (4.1), which is a reduced form of (5.1).

Notice that this kinematic argument makes no appeal to linearity in the stress-

strain law, since it makes no reference to stress at all. Thus, it applies equally to any

kind of material behaviour, including an elastic-plastic material loaded beyond the

yield stress, a non-linear elastic material, or a generally anisotropic material.

As in §4.1, we can establish a relation between the constants C

and the radii

of curvature of the beam, leading to the alternative expression

= C

−

. (5.2)

It is sometimes convenient to deﬁne a Cartesian coordinate system aligned with the

resultant bending axis. If x

′

is rotated through

anticlockwise from x,y, where

tan

= −

; sin

= −

; cos

, (5.3)

we have

′

−

; y

′

(5.4)

from (4.40, 4.41). It then follows from (5.1) and the second of (5.4) that

= C

+ y

′

= C

′

, (5.5)

where the resultant curvature

. (5.6)

5.2 Elastic-plastic constitutive behaviour

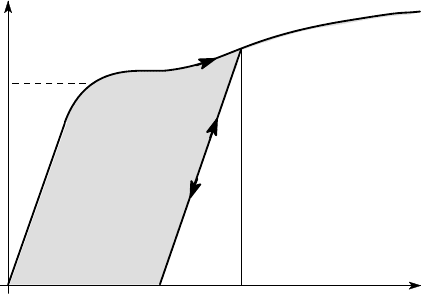
The uniaxial stress strain curve for a typical ductile material is shown in Figure 5.2. It

exhibits a linear elastic region OA, beyond which the curve may be of quite complex

shape. The yield stress S

is deﬁned as that stress beyond which some permanent

deformation is produced — i.e. the stress-strain curve does not return to the point O

on unloading. Experimentally, we need to see a measurable level of permanent strain

to be sure some yield has occurred, so the yield point B is conventionally identiﬁed

as the stress sufﬁcient to leave a permanent tensile strain of 0.2% on unloading. The

yield point B is not necessarily identiﬁed with the limit of proportionality A, though

for metals they are generally very close.

238 5 Non-linear and Elastic-Plastic Bending

Figure 5.2: Uniaxial stress strain curve for a typical ductile material

Beyond the yield point, the stress continues to increase with strain, but the rate of

increase (the slope of the curve) is orders of magnitude lower than that in the linear

elastic range OA.

5.2.1 Unloading and reloading

If the stress is increased into the plastic range and then reduced, the material will

generally unload along a straight line (CD in Figure 5.2) with the same slope as

OA. Reloading from D will follow the same line DC, showing that the unload-

ing/reloading process is elastic until the original maximum stress

Thus a specimen which has been loaded and unloaded along the path OABCD be-

haves as a material with an increased yield stress S

′

(C). In effect, it has become

a new ‘work-hardened’ material. Remember that when we machine a specimen of

a ductile material to perform a tensile test, we have no knowledge of the previous

plastic deformation of the material, for example during the rolling process. We es-

sentially measure just the current properties of the material.

During the loading process, work is done by the applied loads and the speciﬁc

work (i.e. the work done per unit volume of material) is equal to the area under the

stress-strain curve. In the elastic range, this work is stored in the material as strain

energy (see §2.2.3) and is recovered on unloading. Beyond the yield point B, some

of the work done is dissipated as heat and is not recoverable. For the loading path

OABCD, the speciﬁc work done during loading is deﬁned by the area OABCE and

the work recovered during unloading is equal to the triangular area CDE. Thus, the

shaded area OABCD in Figure 5.2 represents the energy dissipated as heat and CDE

represents the elastic strain energy at point C. Notice that the elastic strain energy

increases as a result of work hardening, so not all of the work done between B and C

is dissipated as heat, but for most materials the rate of work hardening is sufﬁciently

slow for this difference to be negligible.

5.2 Elastic-plastic constitutive behaviour 239

5.2.2 Yield during reversed loading

So far we have discussed only those loading scenarios leading to positive (tensile)

stresses, but many engineering applications involve alternating tensile and compres-

sive stresses (see for example §2.3). For isotropic ductile materials, yielding in com-

pression occurs at

= −S

— i.e. at the same stress magnitude as in tensile load-

ing. This result is implicit in both the Tresca and von Mises theories of ductile failure

(§2.2.3).

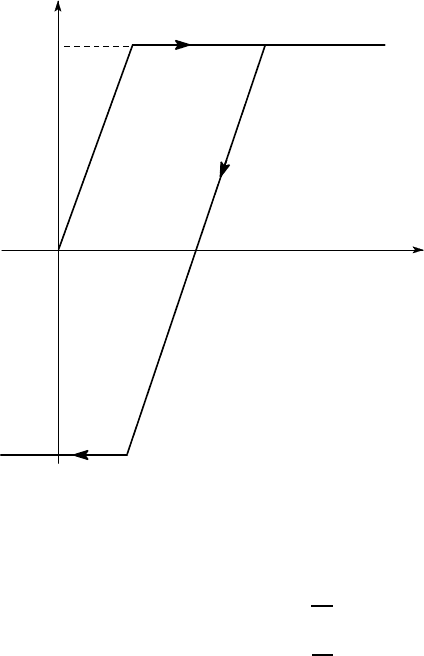
Figure 5.3: Yield during reversed loading

If the material has work hardened, this will generally imply a corresponding in-

crease in compressive yield stress, so that negative loading following the scenario

OABCDF in Figure 5.3 would be expected to involve compressive yield at F, with

CD = DF. This is known as ‘isotropic hardening’, since it assumes that the material

remains isotropic even after plastic deformation. However, signiﬁcant anisotropic ef-

fects are often observed during plastic deformation, since the shape of the grains and

the distribution of dislocations is inﬂuenced by the particular loading scenario. Also,

a drop in the stress for reversed yield is often observed under uniaxial conditions.

This is known as the Bauschinger effect.

The conditions at yield under complex

See for example, F.A. McClintock and A.S. Argon (1966), Mechanical Behaviour of Ma-

terials, Addison-Wesley, Reading MA, §5.8

240 5 Non-linear and Elastic-Plastic Bending

loading scenarios remain a subject of active research, since ﬁnite element methods

now permit complex forming operations to be analysed and the constitutive law for

the material in the plastic r´egime can place limits on the accuracy achievable.

5.2.3 Elastic-perfectly plastic material

In many applications, it is sufﬁcient to use a simpliﬁed constitutive law with no

work hardening — i.e. to assume that the stress remains at a constant yield stress S

during plastic deformation, as shown in Figure 5.4, which also shows the assumed

behaviour for unloading (CD) and for yield under reversed loading (CF). A material

which behaves in this way is described as elastic-perfectly plastic. It represents quite

a good approximation to Figures 5.2, 5.3 as long as the plastic strains are not too

large and this in turn is likely to be true when the plastic zone is adjacent to material

that is still elastic. For example, in the bending of beams, plastic strains sufﬁcient to

cause signiﬁcant work hardening typically require the beam to be bent to a radius

less than about ﬁve times the beam thickness.

Figure 5.4: Constitutive behaviour for an elastic-perfectly plastic material

The loading portion OAC of Figure 5.4 can be described by the equations

= Ee

; |e

| <

(5.7)

= S

sgn(e

) ; |e

| >

, (5.8)

5.3 Stress ﬁelds in non-linear and inelastic bending 241

where the expression sgn(e

) takes the value +1 if e

> 0 and −1 if e

< 0, and is

included to allow for the possibility of compressive loading

< 0, for which the

corresponding strain will be negative.

5.3 Stress ﬁelds in non-linear and inelastic bending

We saw in §5.1 that the tensile strain e

due to bending must be a linear function of

x,y, as deﬁned by equations (5.1, 5.2, 5.5). If the monotonic stress-strain relation is

= f (e

) , (5.9)

the stress will be given by

= f (C

x +C

y) = f



′



. (5.10)

It follows that, as in elastic bending, there will be a neutral axis deﬁned by the straight

line

x +C

y = C

′

= 0 (5.11)

on which the stress

= 0. Also, the stress is constant along any line parallel to the

neutral axis. Indeed, a plot of the stress distribution along y

′

, perpendicular to the

neutral axis, has the same form as the constitutive law except for a linear scaling of

the axis.

These results apply for any function f (e

) in equation (5.9) and can therefore

be used for beams made of non-linear elastic materials as well as for elastic-plastic

bending.

For the special case of an elastic-perfectly plastic material, substitution of (5.5)

into (5.7, 5.8) gives

= EC

′

;



′



< S

(5.12)

= S

sgn



′



;



′



> S

. (5.13)

Thus, there will be an elastic region bounded by the two parallel lines

′

= ±S

, (5.14)

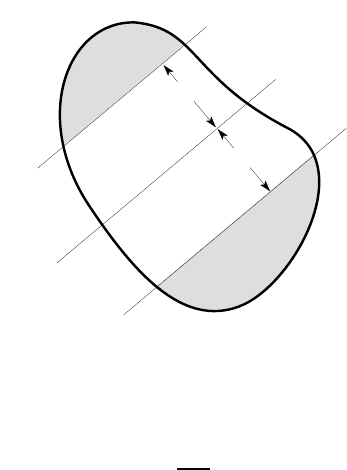
which are also parallel to and equidistant from the neutral axis, as shown in Figure

5.5.

242 5 Non-linear and Elastic-Plastic Bending

plastic

elastic

neutral

axis

plastic

σ = S

σ = −S

Figure 5.5: Elastic and plastic zones in a beam cross section

The perpendicular distance between each line and the neutral axis is

d =

. (5.15)

Outside these lines, the material will have yielded and the stress will be equal

to ±S

, the positive sign being taken on one side and the negative on the other. At

sufﬁciently small applied moments, R will be large and the two bounding lines will

lie outside the beam cross section, all of which will therefore lie in the linear elastic

range. However, at some critical bending moment, denoted by M

, one or both of

the bounding lines will touch the section and yielding will start. We refer to M

the moment for ﬁrst yield. Further increase in moment will cause the bounding lines

to move closer together, increasing the size of the plastic zone at the expense of the

elastic zone.

The maximum moment that can be carried, M

, occurs when the elastic zone

has shrunk to zero. Equation (5.15) shows that this requires that the curvature be

unbounded (i.e. that the radius of curvature R be zero) so it represents local collapse

of the beam. A point in a beam where this has happened is known as a plastic hinge

(see §5.8 below). The moment M

is known as the fully-plastic moment for the beam

section.

5.3.1 Force and moment resultants

If the constants C

deﬁning the strain ﬁeld are known, we can compute the

force and moment resultants F,M

by substituting (5.10) into (4.9, 4.13, 4.14) —

i.e.

F =

dA ; M

ydA ; M

= −

xdA (5.16)

5.4 Pure bending about an axis of symmetry 243

and evaluating the integrals. In the more usual case where F,M

are speciﬁed,

(5.16) provides three simultaneous equations which can be solved for the three un-

knowns C

, after which substitution in (5.10) deﬁnes the complete stress dis-

tribution in the beam.

However, the problem is non-trivial because the non-linearity of the constitu-

tive law (5.9) causes the resulting equations to be non-linear. In addition, we can no

longer treat the three resultants separately and use superposition. For a general un-

symmetrical section or a beam loaded by both an axial force and a bending moment,

the neutral axis is likely to move and rotate as the loads increase and most cases are

sufﬁciently complex to require a numerical solution.

5.4 Pure bending about an axis of symmetry

The solution is considerably simpliﬁed if:-

(i) there is no axial force,

(ii) the beam cross section is symmetric about the axis of the applied bending mo-

ment, and

(iii) the relation between stress and strain is the same in tension and compression,

since the neutral axis must then coincide with the axis of symmetry.

To prove this result, we ﬁrst adopt it as a tentative hypothesis, in which case

. (5.17)

Substituting for

from (5.10) into (5.16), we then obtain

F =





dA ; M





ydA ; M

= −





xdA . (5.18)

In view of the symmetry of the beam cross section, symmetrically disposed el-

ements dA with equal and opposite values of y will make equal and opposite con-

tributions to the ﬁrst and third of these integrals as long as f (y/R) = −f (−y/R) as

required by condition (iii) above. Thus, the conditions F = 0, M

= 0 are satisﬁed

identically by the choice of the symmetry axis as neutral axis, justifying this ini-

tial assumption. The second of (5.18) then deﬁnes the relation between the bending

moment M

and the radius of curvature of the beam R.

Example 5. 1

A rectangular beam of (horizontal) width b and height h is made of a rubber for

which the uniaxial constitutive law is approximated by the equation

= E





244 5 Non-linear and Elastic-Plastic Bending

where E, e

are material constants. Find the relation between the bending moment

M and the radius of curvature R for bending about a horizontal axis.

If the material fails at a tensile stress

= Ee

, ﬁnd the largest moment that can

be transmitted by the beam.

Using equation (5.17) and the given constitutive law, we have

= E





The second of (5.16) or (5.18) gives

M = E

h/2

−h/2

b/2

−b/2





ydxdy = Eb

h/2

−h/2





ydy

= Eb



12R

160R



which deﬁnes the required relation between M and R.

The maximum tensile stress occurs at y= h/2 and is

max

= E





Thus, failure will occur when





= e



2Re





2Re



= 1 ,

which has the solution

2Re

= 0.682 or R = 0.733

The bending moment at this limiting condition is

max

= Eb



12 ×0.733

160 ×(0.733)



= 0.1296Ebh

5.4.1 Symmetric problems for elastic-perfectly plastic materials

The elastic-perfectly plastic constitutive law of equations (5.7, 5.8) has the same be-

haviour in tension and compression and hence satisﬁes condition (iii) above. As in

Figure 5.5, there will be a central elastic region and symmetrically disposed plas-

tic regions yielded in tension and compression respectively. The bending moment-

curvature relation can be determined exactly as in the preceding example, but the

discontinuity at

necessitates breaking the integral into three parts — one for

the central elastic region and one for each of the plastic regions.