Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

3.9 The stiffness matrix 145

4EI

from equations (3.89). There will also be reactions induced at the support A and given

by equations (3.90), but these do not feature in the stiffness matrix because there are

no degrees of freedom at A.

To hold the beam segment BC in the deformed conﬁguration of Figure 3.30 (b),

we shall require a vertical force at B and a clockwise moment

4EI

from equations (3.89). In addition an equal and opposite vertical reaction force will

be induced at C, along with a clockwise reaction moment

2EI

from equations (3.90). The vertical forces do not appear in the stiffness matrix, since

there can be no corresponding vertical displacement at B,C.

The forces and moments required to sustain the conﬁguration 3.30 (b) are the

sum of those required for the beam segments AB, BC considered separately and are

therefore

F = −

6EI

; M

8EI

; M

2EI

An exactly similar argument applied to the rotation

shows that the required

forces and moments will be

F = −

6EI

; M

2EI

; M

8EI

Figure 3.30 (c) shows the conﬁguration obtained when u is the only non-zero

displacement. The beam segment BC translates without deformation and the required

forces and moments are readily found from equations (3.89) as

F =

24EI

u ; M

= −

6EI

u ; M

= −

6EI

u .

Thus, the stiffness formulation for the problem can be written in the matrix form



























24 −6L −6L

−6L 8L

−6L 2L



























. (3.91)

If we wish to obtain the displacements and rotations at B,C due to a speciﬁed set

of loads, all we have to do is to invert this matrix to obtain the compliance matrix C

and then use equation (3.86).

146 3 Energy Methods

3.9.2 Assembly of the stiffness matrix

The forces and moments required to cause a single node to displace or rotate will

contain contributions from each of the components connected to that node. These

contributions can be summed, as in Example 3.11, using tabulated results for stan-

dardized components such as those given in equations (3.89, 3.90). Since the differ-

ent components will generally be in different orientations, it is usually necessary to

perform some coordinate transformation on these tabulated results to refer them to

the coordinate system used for the system as a whole.

The process of summing the contributions from the separate components is re-

ferred to as the assembly of the stiffness matrix. This method is widely used, partic-

ularly in the elastic analysis of civil engineering structures,

which are often made

up of beam segments. Generally, the number of degrees of freedom is large and nu-

merical solution is required.

Essentially the same assembly procedure is used to obtain the global stiffness ma-

trix in the ﬁnite element method, using the load-displacement characteristics of the

individual elements in place of equations (3.89, 3.90). This will be further discussed

in Appendix A (§A.2.2).

3.10 Castigliano’s second theorem

In section §3.8.1, we showed that the strain energy U can be written in terms of the

applied forces and the inﬂuence coefﬁcients as

U =

∑

i=1

∑

j=1

i j

, (3.92)

from equation (3.79). An alternative form of this expression can be obtained by using

(3.74) to substitute for the sum on j, with the result

U =

∑

i=1

. (3.93)

We can then substitute for F

from (3.87) to obtain

U =

∑

i=1

∑

j=1

i j

, (3.94)

which deﬁnes the strain energy in terms of the displacement components u

and the

stiffness coefﬁcients K

i j

Suppose we differentiate (3.94) with respect to u

. The only non-zero terms that

will remain after differentiation will be those containing u

and these will occur in the

See for example, J.B. Kennedy and M.K.S. Madugula (1990), Elastic Analysis of Struc-

tures: Classical and Matrix methods, Harper & Row, New York, Chapter 12.

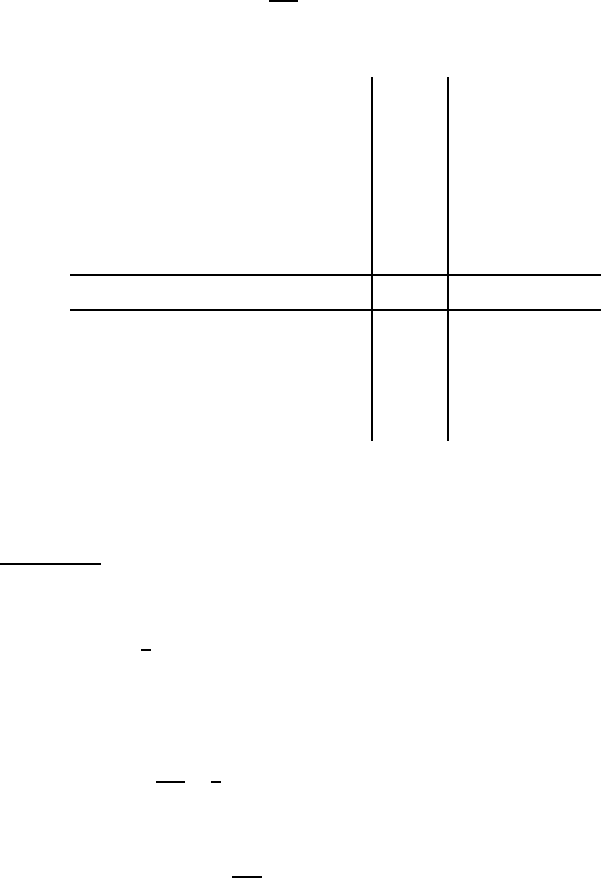
3.10 Castigliano’s second theorem 147

ith row and the ith column of the matrix K, as shown in Figure 3.31. In view of the

reciprocal theorem, K

i j

= K

and hence each term in the double summation

(3.94) occurs twice except the term on the diagonal K

, whose derivative however

also acquires a factor of 2 because u

is squared.

This factor cancels the 1/2 in

(3.94) and we obtain

∂

∑

j=1

i j

. (3.95)

···

··· K

···

··· K

···

··· K

· · · ···

· ··· ·

· · · ···

· ··· ·

· · · ···

· ··· ·

· · · ···

· ··· ·

··· K

· · · ··· · ··· ·

· · · ···

· ··· ·

· · · ···

· ··· ·

· · · ···

· ··· ·

···

··· K

Figure 3.31: Terms in the double summation (3.94) involving a speciﬁc displacement

component u

This argument is perhaps easier to follow by considering a particular example. Suppose

there are only three external forces, in which case, (3.94) can be written

U =



+ K



Differentiating with respect to u

(say), gives

∂

+ K

+ 2K

)

which, using the reciprocal theorem, reduces to

∂

= K

+ K

agreeing with (3.95).

148 3 Energy Methods

Furthermore, we can use (3.87) to substitute for the right hand side of (3.95),

obtaining

∂

= F

. (3.96)

This constitutes another proof of Castigliano’s ﬁrst theorem [equation (3.70)].

However, we should note that the present proof, being based on the stiffness matrix

formulation, implies that the structure is linear, whereas no such limitation applies to

the proof given in §3.7.

An exactly parallel argument can be used with equations (3.92, 3.74) to show

that

∂

∑

j=1

i j

= u

. (3.97)

This is a simpliﬁed version

of Castigliano’s second theorem.

As in §3.7, we should note that the partial derivative implies that all the forces

other than F

are being held constant.

This might be indicated, as before, by writing



∂



( j6=i)

3.10.1 Use of the theo rem

Castigliano’s second theorem permits us to ﬁnd any displacement component, pro-

vided the strain energy can be written in terms of the external forces F

. If the struc-

ture is determinate,

we can do this using equilibrium arguments only. Thus, the

theorem is generally used in combination with an equilibrium analysis and replaces

the kinematic arguments in the direct method. This contrasts with the principle of

stationary potential energy (§ 3.5) and Castigliano’s ﬁrst theorem (§3.7), which are

used in combination with kinematic analysis and replace the equilibrium arguments.

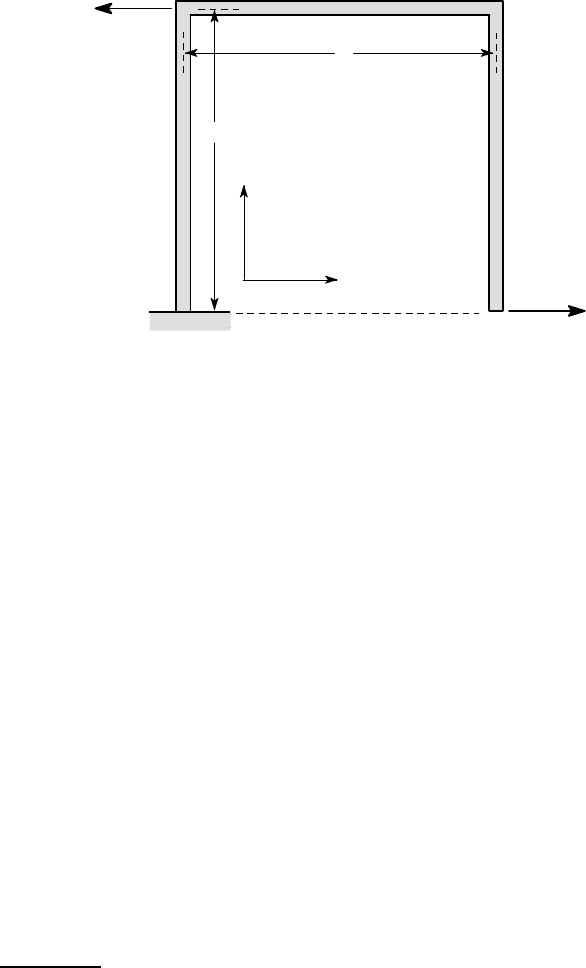
Example 3. 12

The inverted U structure of Figure 3.32 is subjected to two horizontal forces F

as shown. Determine the horizontal displacement of the free end D. All sections of

the structure have the same ﬂexural rigidity EI and are of length L.

The more general version of the theorem refers to a quantity known as complementary

energy, C =

∑

i=1

−U. Complementary energy and strain energy are equal for elastic

systems and small displacements, as can be seen from (3.93) and the deﬁnition of C. When

the system is non-linear, C and U will generally differ, but Castigliano’s second theorem

is still applicable, provided U is replaced by C. For more details on such applications, the

student is referred to more advanced texts on energy and variational methods.

Another way of saying this is that the F

are treated as an orthogonal set of generalized

coordinates.

We shall consider extensions to indeterminate structures in §3.10.5 below.

3.10 Castigliano’s second theorem 149

Figure 3.32: A frame structure, built-in at A and loaded at B and D

Following the discussion in §3.3 above, we shall assume that only the strain en-

ergy stored in bending is signiﬁcant, which is equivalent to neglecting the extension

of the horizontal section of the frame (for example) due to the axial force in compar-

ison with the deﬂections due to bending.

Each part of the frame will store strain energy and the total energy U will be

the sum of that in each part. The procedure is to draw free-body diagrams for each

part in turn, determine the bending moment as a function of position along the beam

and substitute in expressions similar to equation (3.24). Finally, we sum the energy

expressions for the three parts and apply Castigliano’s second theorem (3.97).

Figure 3.33 shows the three free-body diagrams appropriate to the three beam

segments AB, BC,CD. Notice that to ﬁnd the bending moment in a particular segment

(say in AB), we make an imaginary cut at an arbitrary location a distance y from

A and then draw a free-body diagram of one of the two pieces separated by the

cut, showing all the forces that act on that piece.

The dimensions x,y deﬁning the

cuts in Figures 3.33 (a,b,c) are suggested by an implied Cartesian coordinate system

centred on A, but any convenient deﬁnition can be used — for example, we could

have measured x from C in the segment BC, in which case (L−x) would be replaced

by x, with some slight simpliﬁcation in the evaluation of U

below. Notice also that

we could have replaced Figure 3.33 (a) by the simpler segment AC

, but we would

then need to know the reactions at the support A, which would require a preliminary

statical analysis of the whole structure.

A common error is to make the cut correctly, but then only to show that part of the beam

going from the cut to the point B (say), neglecting the fact that there are internal forces and

moments at B. Imagine making the cut with a hacksaw and see in your mind’s eye the piece

that drops off.

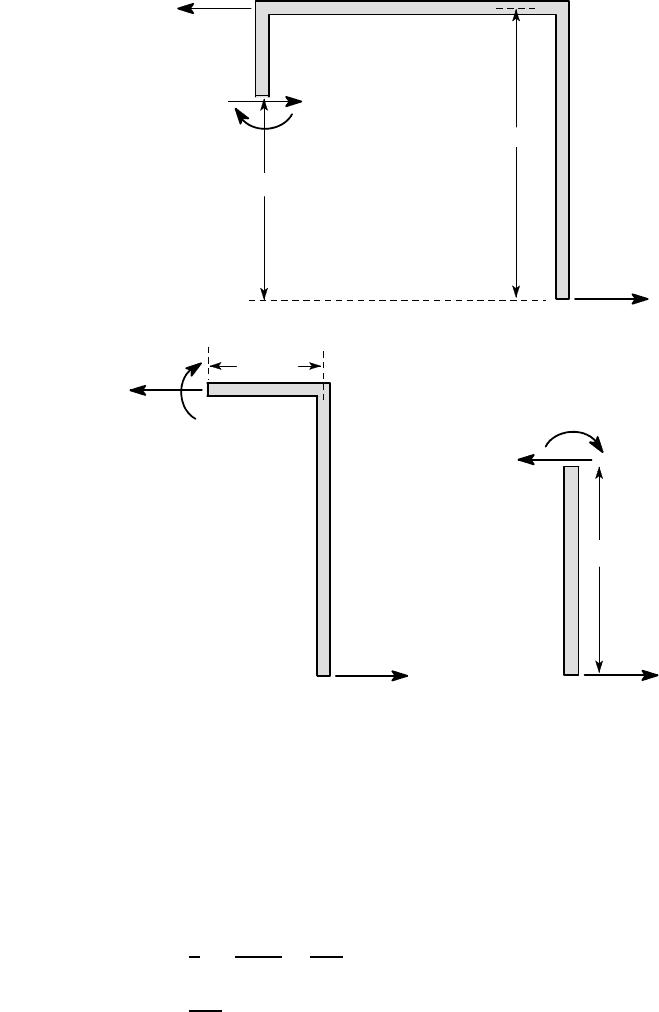
150 3 Energy Methods

(a)

(L - x)

(b) (c)

Figure 3.33: Free-body diagrams for the problem of Figure 3.32

Taking moments about the point C

for the segment C

BCD in Figure 3.33 (a),

we ﬁnd

= F

y + F

(L −y)

and hence, using equation (3.24), the strain energy stored in the segment AB is

2EI

+ 2F

y(L −y) + F

(L −y)

6EI



+ F



3.10 Castigliano’s second theorem 151

after evaluating the integrals. Similarly, from Figures 3.33 (b,c), we have

= F

in BC, CD respectively and the corresponding strain energy expressions are

2EI

dy =

2EI

dy =

6EI

The total strain energy in the structure is therefore

U = U

6EI



+ F



2EI

6EI



+ F



To determine the horizontal displacement at D, we now apply Castigliano’s sec-

ond theorem (3.97) to obtain

∂

6EI

(10F

+ F

) , (3.98)

which is the required result.

3.10.2 Dummy loads

Castigliano’s second theorem enables us to determine the displacement of the point

of application of any external force in the direction of that force, no matter how many

external forces there are, in contrast to the method of §3.3 which only worked if there

was only one external force. Thus, in Example 3.12, we could also ﬁnd the horizontal

displacement of the point B by taking the derivative with respect to F

However, we often want to ﬁnd displacements in a direction or at a point where

there are no external forces. We can do this by the simple device of putting a dummy

force Q at the point where the displacement is to be found. We then proceed with the

calculation of the required displacement and afterwards, set the dummy force Q to

zero.

Example 3. 13

Figure 3.34(a) shows a uniform cantilever beam of length L and ﬂexural rigidity EI,

subjected to a uniformly distributed load w

per unit length in the segment a<z< L.

Find the downward vertical displacement at the end A of the cantilever.

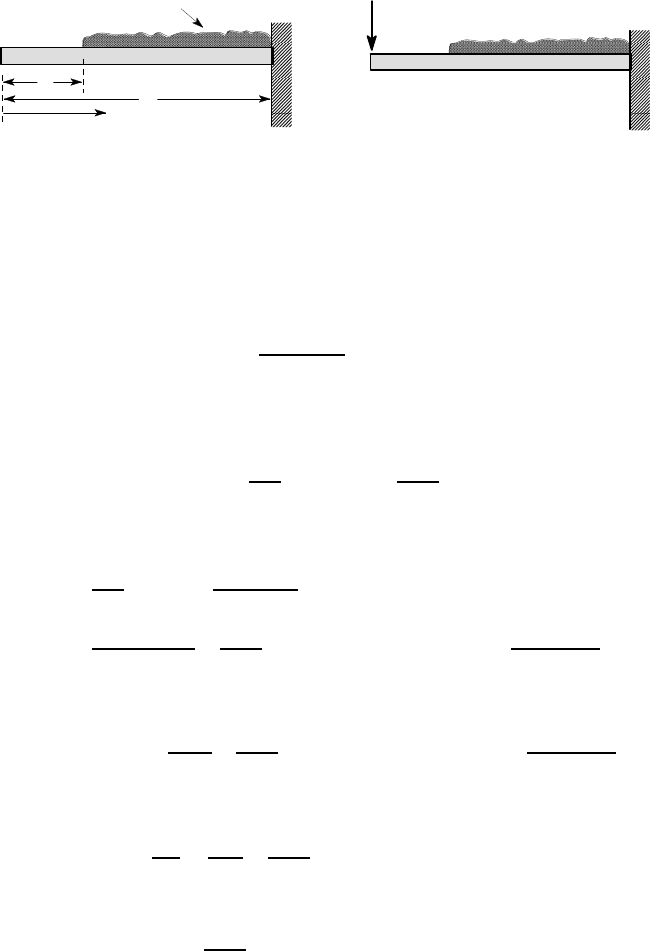
152 3 Energy Methods

Figure 3.34: Cantilever beam subjected to a distributed load w

We ﬁrst place a downward dummy force Q at the end of the beam, as shown in

Figure 3.34 (b). With the dummy force in place, the bending moment in the beam is

M = Qz ; 0 < z < a

= Qz +

(z −a)

; a < z < L . (3.99)

As in previous examples, we calculate the strain energy in the two regions AB

and BC separately and add the result to get the total strain energy. In AB, we have

2EI

dz =

6EI

whilst, in BC,

2EI



Qz +

(z −a)





−a



6EI

24EI



−8aL

+ 6a

−a



(L −a)

40EI

The total strain energy is therefore

U = U

6EI

24EI



−8aL

+ 6a

−a



(L −a)

40EI

We now apply Castigliano’s second theorem to obtain the displacement at A,

which is

∂

3EI

24EI



−8aL

+ 6a

−a



and ﬁnally set the dummy force Q to zero, obtaining

24EI



−8aL

+ 6a

−a



, (3.100)

which is the required result.

It is important to note that the dummy force Q cannot be set to zero until after

the differentiation

∂

Q has been performed, since otherwise the differentiation

would yield a trivial result.

w per unit length

A B

(a) (b)

3.10 Castigliano’s second theorem 153

Example 3. 14

Use Castigliano’s second theorem to ﬁnd the horizontal displacement u

of the point

A, in Example 3.2

Figure 3.35: Force supported by two springs

In order to ﬁnd the horizontal displacement, we need to introduce a horizontal

dummy force Q in addition to the applied vertical force F, as shown in Figure 3.35.

The equilibrium equations (3.16, 3.17) are therefore modiﬁed to

+ F

cos30

−Q = 0

sin30

+ F = 0

with solution

= Q +

√

3F ; F

= −2F .

As before, the strain energy in the two springs is calculated as

U =

(Q +

√

3F)

(−2F)

and the horizontal displacement is then given by

∂

(Q +

√

3F)

Finally, we set Q=0, with the result

√

, (3.101)

agreeing with (3.45) which was obtained rather more laboriously by the stationary

potential energy method.

154 3 Energy Methods

3.10.3 Unit load method

In the above examples, the algebra is complicated by the fact that the forces or mo-

ments are squared in the expressions for strain energy, but the expressions simplify

considerably when the differentiation is performed and when the dummy load (if

any) is set to zero. We can avoid some of this algebraic complexity, at the cost of a

little clarity in the method, by changing the order in which these operations are per-

formed. To illustrate this, we shall repeat the calculations for Example 3.13, using

the alternative procedure.

We ﬁrst note that the strain energy can be written symbolically in the form

U = U

2EI

dz +

2EI

dz , (3.102)

where M is given by (3.99). We can perform the differentiation before the integration,

with the result

∂

dz +

∂

dz . (3.103)

Now that the differentiation has been performed, we can set Q to zero. Thus, the

displacement u

can be evaluated from equation (3.103) using the simpler equations

M = 0 ; 0 < z < a

(z −a)

; a < z < L (3.104)

[obtained by setting Q= 0 in (3.99)] and

∂

= z ; 0 < z < a

= z ; a < z < L ,

obtained by differentiation of (3.99).

Substituting these results into (3.103), we obtain

(z −a)

zdz

24EI



−8aL

+ 6a

−a



, (3.105)

as before. Notice that the ﬁrst of the two integrals in (3.103) degenerates to zero,

since M is zero in this range from equation (3.104).

This procedure is known as the unit load method, since the expressions for

∂

Q can be interpreted as the moments induced by a dummy load Q of unit

magnitude.