Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.

71
i=Ñ/t u
ãë
D
à
)
G=t
D
Ñ/
u
n
+
1
i
n
+
1
i=i
ãí
á
)
G=t/L
D
u
n
+
1
i
n
+
1
Ðèñ. 2.24
+++
DD
=-=-
111
nnnnn
tt
iuuGuGu
LL
,
ãäå G = Dt/L.
Íà ðèñ. 2.24, á ïîêàçàíà ýêâèâàëåíòíàÿ äèñêðåòíàÿ ñõåìà çà-
ìåùåíèÿ L-ýëåìåíòà.
Èñïîëüçîâàíèå äèñêðåòíûõ ìîäåëåé ýëåìåíòîâ ïîçâîëÿåò ñâåñòè
RLC-öåïü ê ñîîòâåòñòâóþùåé ðåçèñòèâíîé öåïè, ÷òî ñóùåñòâåííî
óïðîñòèò èõ ìàøèííûé àíàëèç.
Âîïðîñû è çàäàíèÿ äëÿ ñàìîïðîâåðêè
1. Ïðèíöèï ñîñòàâëåíèÿ óðàâíåíèé ìåòîäîì çàêîíîâ Êèðõãîôà.
2. Êàêèå òîêè è íàïðÿæåíèÿ îñòàþòñÿ íåèçìåííûìè ïðè ïåðåõîäå
îò ñîåäèíåíèÿ «òðåóãîëüíèêà» â «çâåçäó» è îáðàòíî?
3. ×åì îïðåäåëÿåòñÿ êîëè÷åñòâî ÷àñòè÷íûõ ñõåì ïðè ðàñ÷åòå òîêîâ
â öåïè ìåòîäîì íàëîæåíèÿ?
4. Êàêèå çàêîíû Êèðõãîôà èñïîëüçóþòñÿ ïðè ñîñòàâëåíèè óðàâíå-
íèé ïî ìåòîäàì êîíòóðíûõ òîêîâ è óçëîâûõ íàïðÿæåíèé?
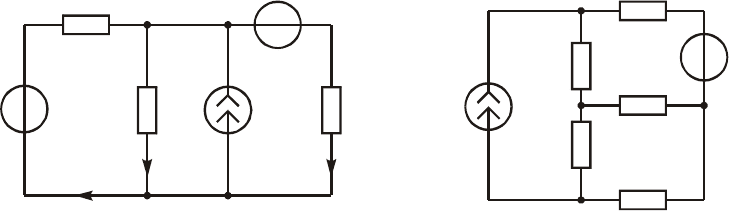
5. Ðàññ÷èòàòü òîêè âåòâåé â öåïè ðèñ. 2.26 ìåòîäàìè íàëîæåíèÿ çà-
êîíîâ Êèðõãîôà, êîíòóðíûõ òîêîâ, óçëîâûõ íàïðÿæåíèé, åñëè
èçâåñòíî, ÷òî: U
ã1
= 5 Â; U
ã3
= 10 Â; J = 0,5 À; R
1
= R
2
= R
3
=
= 10 Îì.
Îòâåò: I
1
= 0,5 À; I
2
= 0 À; I
3
= 1 À.
6. Êàêèå òåîðåìû èñïîëüçóþòñÿ ïðè îïðåäåëåíèè òîêà â îòäåëüíî
âçÿòîé âåòâè ìåòîäîì ýêâèâàëåíòíîãî ãåíåðàòîðà?
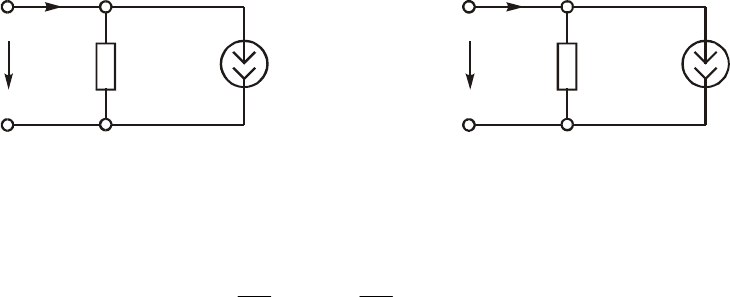
7. Ìåòîäîì ýêâèâàëåíòíîãî ãåíåðàòîðà â öåïè ðèñ. 2.24 îïðåäåëèòü
ñîïðîòèâëåíèå R
5
, êîãäà â íåì âûäåëÿåòñÿ ìàêñèìàëüíàÿ
ìîùíîñòü, åñëè U = 3 Â; J = 0,5 À; R
1
= R
2
= R
3
= R
4
=
= 2 Îì.
Îòâåò: R
5
= 3,33 Îì; Ð = 216 ìÂò.
8. Â ñîãëàñîâàííîì èëè íåñîãëàñîâàííîì ðåæèìå ðàáîòàþò âûñîêî-
òî÷íûå àòòåíþàòîðû è ïî÷åìó?
72
R
3
I
2
U
ã
1
+
I
3
R
2
J
R
1
U
ã
3
I
1
+
R
4
R
2
R
5
+
J
R
1
R
3
U
Ðèñ. 2.25 Ðèñ. 2.26
9. Îïðåäåëèòü â àòòåíþàòîðå, èçîáðàæåííîì íà ðèñ. 2.15, ðåçèñòî-
ðû R
1
è R
2
, åñëè èçâåñòíî ÷òî R
0
= 50 Îì; Ê = 0,1.
Îòâåò: R
1
= 450 Îì; R
2
= 5,55 Îì.
10. ×åì îïðåäåëÿþòñÿ êîýôôèöèåíòû ïåðåäà÷è ìàñøòàáíûõ óñèëè-
òåëåé, âêëþ÷åííûõ ïî èíâåðòèðóþùåé è íåèíâåðòèðóþùåé
ñõåìàì?
11. Äëÿ êîíâåðòîðà îòðèöàòåëüíîãî ñîïðîòèâëåíèÿ, èçîáðàæåííîãî
íà ðèñ. 2.21, îïðåäåëèòü R
1
, åñëè R
âõ
= 1 êÎì; R
í
= 50 Îì;
R
2
= 500 Îì.
Îòâåò: R
1
= 25 Îì.
12.  ÷åì îñîáåííîñòè àëãîðèòìîâ àíàëèçà ëèíåéíûõ ðåçèñòèâíûõ
öåïåé íà ÝÂÌ ìåòîäîì óçëîâûõ ïîòåíöèàëîâ?
ÃËÀÂÀ 3. ËÈÍÅÉÍÛÅ ÝËÅÊÒÐÈ×ÅÑÊÈÅ ÖÅÏÈ
 ÐÅÆÈÌÅ ÃÀÐÌÎÍÈ×ÅÑÊÈÕ ÊÎËÅÁÀÍÈÈ
3.1. Ãàðìîíè÷åñêèå êîëåáàíèÿ. Îñíîâíûå ïîíÿòèÿ
è îïðåäåëåíèÿ
Ýëåêòðè÷åñêèå öåïè ìîãóò íàõîäèòüñÿ ïîä âîçäåéñòâèåì ïîñòî-
ÿííûõ èëè ïåðåìåííûõ íàïðÿæåíèé è òîêîâ. Ñðåäè ýòèõ âîçäåéñò-
âèé âàæíåéøóþ ðîëü èãðàþò ãàðìîíè÷åñêèå êîëåáàíèÿ. Ïîñëåäíèå
øèðîêî èñïîëüçóþòñÿ äëÿ ïåðåäà÷è ñèãíàëîâ è ýëåêòðè÷åñêîé
ýíåðãèè, à òàêæå ìîãóò ïðèìåíÿòüñÿ â êà÷åñòâå ïðîñòåéøåãî èñïû-
òàòåëüíîãî ñèãíàëà. Èññëåäîâàíèå ðåæèìà ãàðìîíè÷åñêèõ êîëåáà-
íèé âàæíî è ñ ìåòîäè÷åñêîé òî÷êè çðåíèÿ, ïîñêîëüêó àíàëèç ýëåê-
òðè÷åñêèõ öåïåé ïðè íåãàðìîíè÷åñêèõ âîçäåéñòâèÿõ ìîæíî ñâåñòè
ê àíàëèçó öåïè îò ñîâîêóïíîñòè ãàðìîíè÷åñêèõ âîçäåéñòâèé. Â
ýòîì ñìûñëå ìåòîäèêó àíàëèçà è ðàñ÷åòà öåïåé ïðè ãàðìîíè÷åñêèõ
âîçäåéñòâèÿõ ìîæíî ðàñïðîñòðàíèòü è íà öåïè ïðè ïåðèîäè÷åñêèõ
íåñèíóñîèäàëüíûõ, à òàêæå íåïåðèîäè÷åñêèõ âîçäåéñòâèÿõ (ñì.
ãë. 5, 9).

73
I
m
it
()
T
j
i
/
w
t
Ðèñ. 3.1
Ãàðìîíè÷åñêîå êîëåáàíèå i(t)
(ðèñ. 3.1) õàðàêòåðèçóåòñÿ ñëåäóþ-
ùèìè îñíîâíûìè ïàðàìåòðàìè: àìï-
ëèòóäîé I
ò
; óãëîâîé ÷àñòîòîé w,
íà÷àëüíîé ôàçîé j
i
. Àìïëèòóäîé
íàçûâàþò ìàêñèìàëüíîå àáñîëþòíîå
çíà÷åíèå òîêà i (t). Àíàëèòè÷åñêè
ãàðìîíè÷åñêîå êîëåáàíèå ìîæíî çà-
ïèñàòü â âèäå
(
)
(
)
(
)
==Y
w+j
sinsin
mmi
i
iII
t
tt
(3.1)
ãäå Y
i
(t) = wt + j
i
$ íàçûâàåòñÿ òåêóùåé ôàçîé (èëè ïðîñòî ôàçîé)
ãàðìîíè÷åñêîãî êîëåáàíèÿ, òàê êàê îíà ðàñòåò ëèíåéíî âî âðåìåíè ñ
óãëîâîé ñêîðîñòüþ w = dY
i
/dt. Âìåñòî ôîðìóëû (3.1) ãàðìî-
íè÷åñêîå êîëåáàíèå ìîæíî âûðàçèòü è â êîñèíóñîèäàëüíîé ôîðìå:
(
)
(
)
¢
=
w+j
cos
m
i
iI
t
t
, (3.2)
ãäå j
i
¢ = j
i
+p/2.
Íàèìåíüøèé ïðîìåæóòîê âðåìåíè, ïî èñòå÷åíèè êîòîðîãî çíà÷åíèÿ
ôóíêöèè i (t) ïîâòîðÿþòñÿ, íàçûâàåòñÿ ïåðèîäîì Ò. Ìåæäó ïåðèî-
äîì Ò è óãëîâîé ÷àñòîòîé w ñóùåñòâóåò ïðîñòàÿ ñâÿçü:
=pw
2T
. (3.3)
Âåëè÷èíó, îáðàòíóþ ïåðèîäó, íàçûâàþò öèêëè÷åñêîé ÷àñòî-
òîé: f = l/T. Èç âûøåèçëîæåííîãî ñëåäóåò, ÷òî w = 2pf. Åäèíèöåé
èçìåðåíèÿ ÷àñòîòû f ÿâëÿåòñÿ ãåðö (Ãö), óãëîâîé ÷àñòîòû w $ ðàäè-
àí â ñåêóíäó (ðàä/ñ). Òàê êàê ðàäèàí $ âåëè÷èíà áåçðàçìåðíàÿ, òî
[w] èçìåðÿåòñÿ â 1/ñ èëè ñ
$1
.
 ðàäèîòåõíèêå è ýëåêòðîñâÿçè èñïîëüçóþò ãàðìîíè÷åñêèå ñèã-
íàëû îò äîëåé ãåðö (èíôðàíèçêèå ÷àñòîòû) äî äåñÿòêîâ è ñîòåí ãè-
ãàãåðö (ñâåðõâûñîêèå ÷àñòîòû).
Äëÿ ïèòàíèÿ ðàçëè÷íûõ ýëåêòðîýíåðãåòè÷åñêèõ óñòàíîâîê â
Ðîññèè è ðÿäå äðóãèõ ñòðàí ïðèíÿòà ïðîìûøëåííàÿ ÷àñòîòà
f = 50 Ãö.  êà÷åñòâå èñòî÷íèêîâ ãàðìîíè÷åñêèõ êîëåáàíèé ïðî-
ìûøëåííîé ÷àñòîòû èñïîëüçóþòñÿ ýëåêòðîìàøèííûå ãåíåðàòîðû
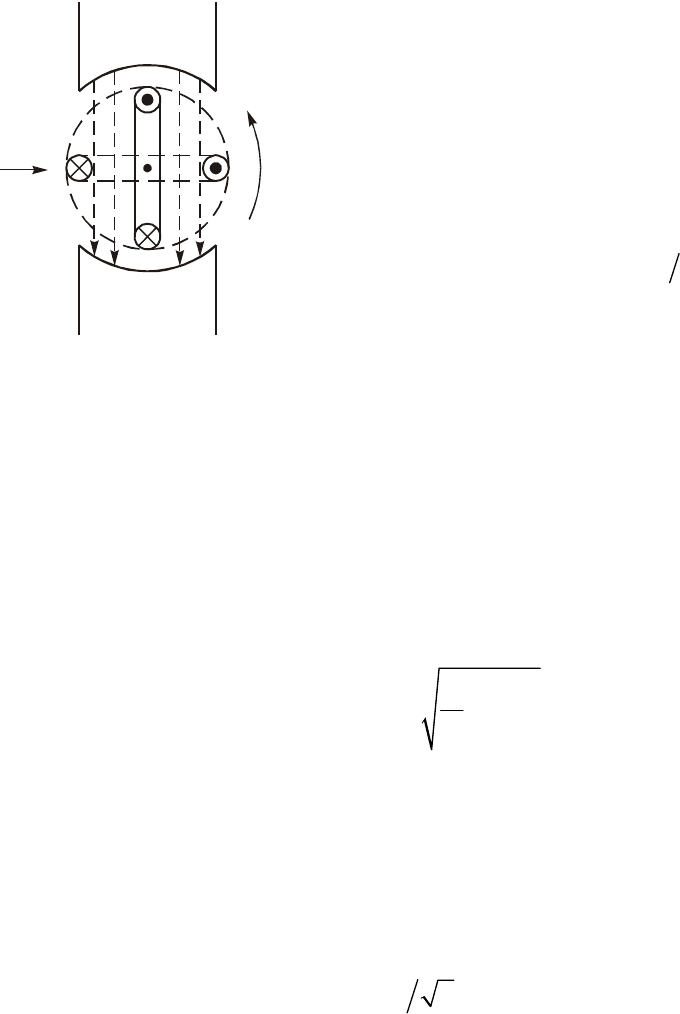
ðàçëè÷íîãî òèïà. Ïðèíöèï ðàáîòû ïðîñòåéøåãî ýëåêòðîìàøèííî-
ãî ãåíåðàòîðà èëëþñòðèðóåò ðèñ. 3.2. Â ñîñòàâ ãåíåðàòîðà âõîäÿò:
ñòàòîð, ñîçäàþùèé ìàãíèòíîå ïîëå ñ ìàãíèòíîé èíäóêöèåé Â, è
ðîòîð, âðàùàþùèéñÿ â ýòîì ìàãíèòíîì ïîëå ñ óãëîâîé ÷àñòîòîé
w. Ïðè ïåðåñå÷åíèè âèòêàìè êàòóøêè ðîòîðà ìàãíèòíîãî ïîòîêà
Ô â íèõ ñîãëàñíî çàêîíó ýëåêòðîìàãíèòíîé èíäóêöèè íàâîäèòñÿ
ÝÄÑ
YF
=-=-
dd
ew
dtdt
, (3.4)
74
jj
Ñòàòîð
Ñòàòîð
S
N
w
Ðîòîð
Â
Ðèñ. 3.2
ãäå Y = wÔ $ ïîòîêîñöåïëåíèå
êàòóøêè ñ ìàãíèòíûìè ïîòîêàìè; w $
÷èñëî âèòêîâ êàòóøêè. Ïðè ïîñ-
òîÿííîé ñêîðîñòè âðàùåíèÿ ðîòîðà
äëÿ ïîëó÷åíèÿ ÝÄÑ ñèíóñîèäàëüíîé
ôîðìû ïðèìåíÿþòñÿ ïîëþñà ñïåöè-
àëüíîé ôîðìû. ×àñòîòà íà âûõîäå ãå-
íåðàòîðà
=
60
n
fpv ,
ãäå ð
ï
÷èñëî ïàð ïîëþñîâ ðîòîðà;
v $ ÷àñòîòà âðàùåíèÿ ðîòîðà, îá/ìèí.
Ýëåêòðîìàøèííûå ãåíåðàòîðû èñ-
ïîëüçóþòñÿ äëÿ ïîëó÷åíèÿ ãàðìîíè-
÷åñêèõ íàïðÿæåíèé è òîêîâ íå âûøå
5...8 êÃö. Äëÿ ïîëó÷åíèÿ ãàðìîíè÷åñêèõ ñèãíàëîâ áîëåå âûñîêèõ
÷àñòîò îáû÷íî èñïîëüçóþòñÿ ëàìïîâûå è ïîëóïðîâîäíèêîâûå ãåíå-
ðàòîðû (ñì. ãë. 15).
Âàæíûìè ïàðàìåòðàìè ãàðìîíè÷åñêèõ êîëåáàíèé ÿâëÿþòñÿ èõ
äåéñòâóþùåå è ñðåäíåå çíà÷åíèÿ. Äåéñòâóþùåå çíà÷åíèå ãàðìî-
íè÷åñêîãî òîêà
=
ò
2
0
1
T
Iidt
T
. (3.5)
Çäåñü i = i(t) $ ìãíîâåííîå çíà÷åíèå ãàðìîíè÷åñêîãî òîêà, êî-
òîðîå îïðåäåëÿåòñÿ èç âûðàæåíèÿ
(
)
=
w+j
sin
m
i
iI
t
. (3.6)
Ïîäñòàâèâ çíà÷åíèå i èç (3.6) â (3.5), ïîñëå èíòåãðèðîâàíèÿ äëÿ
äåéñòâóþùåãî çíà÷åíèÿ òîêà ïîëó÷èì
=»
20,707
mm
III
. (3.7)
Àíàëîãè÷íî (3.1)$ (3.5) îïðåäåëÿåòñÿ ìãíîâåííîå è äåéñòâóþ-
ùåå çíà÷åíèÿ íàïðÿæåíèÿ. Òàê, äëÿ äåéñòâóþùåãî çíà÷åíèÿ íà-
ïðÿæåíèÿ ìîæíî çàïèñàòü:
»
0,707
m
UU
.
Äåéñòâóþùèå çíà÷åíèÿ òîêîâ è íàïðÿæåíèé íàçûâàþò åùå èõ
ñðåäíåêâàäðàòè÷åñêèìè çíà÷åíèÿìè.
Îïðåäåëèì òåïëîâóþ ýíåðãèþ, êîòîðàÿ âûäåëÿåòñÿ ãàðìîíè÷å-
ñêèì êîëåáàíèåì i (t) çà ïåðèîä Ò â ðåçèñòèâíîì ýëåìåíòå ñ ñî-
ïðîòèâëåíèåì R:
===
òò
22
00
TT
R
WpdtRidtTRI
. (3.8)

75
Òàêèì îáðàçîì, äåéñòâóþùåå çíà÷åíèå òîêà ÷èñëåííî ðàâíî òàêî-
ìó ïîñòîÿííîìó òîêó, êîòîðûé çà ïåðèîä Ò íà òîì æå ñîïðîòèâëåíèè
âûäåëÿåò òî æå êîëè÷åñòâî òåïëà, ÷òî è ãàðìîíè÷åñêèé òîê.
Ñðåäíåå çíà÷åíèå ãàðìîíè÷åñêîãî òîêà
=
ò
ñð
0
1
T
Iidt
T
. (3.9)
Ïîäñòàâèâ çíà÷åíèå i èç (3.6) â (3.9), íàõîäèì, ÷òî I
ñð
= 0.
Ýòîò ðåçóëüòàò âïîëíå ïîíÿòåí, åñëè ó÷åñòü, ÷òî óðàâíåíèå (3.9)
îïðåäåëÿåò ïëîùàäü, îãðàíè÷åííóþ êðèâîé i (t) çà ïåðèîä Ò (ñì.
ðèñ. 3.1). Åñëè çíà÷åíèå òîêà îïðåäåëåíî çà ïîëïåðèîäà, òî ìîæíî
çàïèñàòü:
()
==»
p
ò
2
ñð
1
0
22
0,637
T
m
m
I
IidtI
T
. (3.10)
Àíàëîãè÷íî îïðåäåëÿåì, ÷òî Uñð(1) » 0,637U
m
.
3.2. Ñïîñîáû ïðåäñòàâëåíèÿ ãàðìîíè÷åñêèõ êîëåáàíèé
Ãàðìîíè÷åñêèå êîëåáàíèÿ ìîæíî ïðåäñòàâèòü ðàçëè÷íûìè ñïî-
ñîáàìè: ôóíêöèÿìè âðåìåíè (âðåìåííûå äèàãðàììû) (ñì.
ðèñ. 3.1); âðàùàþùèìèñÿ âåêòîðàìè (âåêòîðíûå äèàãðàììû); êîì-
ïëåêñíûìè ÷èñëàìè; àìïëèòóäíûìè è ôàçîâûìè ñïåêòðàìè. Òîò
èëè èíîé ñïîñîá ïðåäñòàâëåíèÿ ïðèìåíÿåòñÿ â çàâèñèìîñòè îò õà-
ðàêòåðà ðåøàåìûõ çàäà÷.
Âðåìåííîå ïðåäñòàâëåíèå ãàðìîíè÷åñêèõ êîëåáàíèé íàãëÿäíî,
îäíàêî åãî èñïîëüçîâàíèå â çàäà÷àõ àíàëèçà öåïåé çàòðóäíèòåëüíî,
òàê êàê òðåáóåò ïðîâåäåíèÿ ãðîìîçäêèõ òðèãîíîìåòðè÷åñêèõ ïðå-
îáðàçîâàíèé. Áîëåå óäîáíî âåêòîðíîå ïðåäñòàâëåíèå ãàðìîíè-
÷åñêèõ êîëåáàíèé, ïðè êîòîðîì êàæäîìó êîëåáàíèþ ñòàâèòñÿ â ñî-
îòâåòñòâèå âðàùàþùèéñÿ âåêòîð îïðåäåëåííîé äëèíû ñ çàäàííîé
íà÷àëüíîé ôàçîé.  êà÷åñòâå ïðèìåðà íà ðèñ. 3.3 ïîêàçàíî âåêòîð-
íîå ïðåäñòàâëåíèå äâóõ êîëåáàíèé òîêîâ i
1
è i
2
:
(
)
( )
w+j
ü
=
ï
ý
w+j
=
ï
þ
1
11
2
22
sin
sin
m
m
t
iI
t
iI
(3.11)
Èõ ñóììó i
3
ëåãêî ìîæíî íàéòè ïî ôîðìóëàì ñóììèðîâàíèÿ
âåêòîðîâ:
(
)
w+j
=+=
3
3123
sin
m
t
iiiI , (3.12)
ãäå
( )
j-j
=++
j+j
j=
j+j
22
21
31212
1122
3
1122
2cos;
sinsin
arctg.
coscos
mmmmm
mm
mm
IIIII
II
II
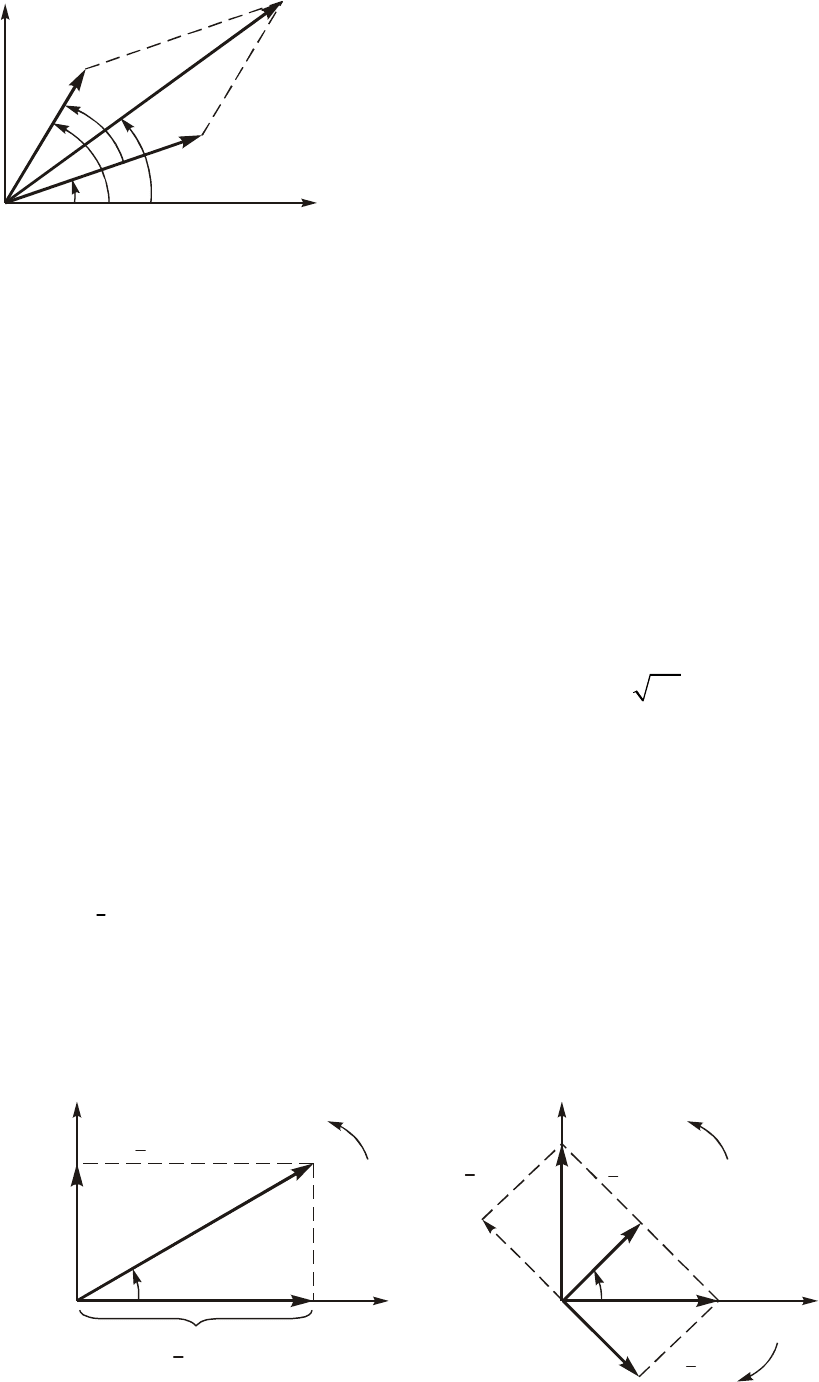
76
+
j
1
j
2
j
3
j
I
m
1
I
m
2
I
m
3
j
0
Ðèñ. 3.3
j
I
m
I
m
{}
Ie
m
jt
w
j
I/
m
2
-I/
m
2
*
w
+
j
0
Re
{}
Ie
m
jt
w
+
j
0
I/
m
2
*
-w
á
)
a
)
Ðèñ. 3.4
Âåëè÷èíà j = j
2
$ j
1
íàçûâàåòñÿ
ôàçîâûì ñäâèãîì ìåæäó êîëåáàíèÿìè
i
1
è i
2
. Îí îïðåäåëÿåòñÿ òîëüêî íà÷àëü-
íûìè ôàçàìè j
1
è j
2
è íå çàâèñèò îò
íà÷àëà îòñ÷åòà âðåìåíè. Íåòðóäíî âè-
äåòü, ÷òî ñóììèðîâàíèå (íàëîæåíèå)
ëþáîãî ÷èñëà ãàðìîíè÷åñêèõ êîëåáàíèé
ñ ÷àñòîòîé w ïðèâîäèò ê ãàðìîíè÷åñêîìó
êîëåáàíèþ òîé æå ÷àñòîòû w.
Ñîâîêóïíîñòü âåêòîðîâ, èçîáðàæà-
þùèõ ãàðìîíè÷åñêèå êîëåáàíèÿ â ýëåêòðè÷åñêîé öåïè, íàçûâàþò
âåêòîðíîé äèàãðàììîé. Âåêòîðíûå äèàãðàììû ìîæíî ñòðîèòü êàê
äëÿ àìïëèòóäíûõ, òàê è äëÿ äåéñòâóþùèõ çíà÷åíèé òîêîâ è íà-
ïðÿæåíèé.
Íàèáîëåå ðàñïðîñòðàíåííûìè ÿâëÿþòñÿ ïðåäñòàâëåíèÿ ãàðìî-
íè÷åñêèõ êîëåáàíèé ñ ïîìîùüþ êîìïëåêñíûõ ÷èñåë. Ýòè ïðåäñòàâ-
ëåíèÿ ëåæàò â îñíîâå ñèìâîëè÷åñêîãî ìåòîäà ðàñ÷åòà ýëåêòðè÷å-
ñêèõ öåïåé $ ìåòîäà êîìïëåêñíûõ àìïëèòóä. Ïðåäñòàâèì òîê i,
îïðåäåëÿåìûé ôîðìóëîé (3.6), íà êîìïëåêñíîé ïëîñêîñòè. Äëÿ
ýòîãî èçîáðàçèì âåêòîð I
m
íà êîìïëåêñíîé ïëîñêîñòè ñ ó÷åòîì íà-
÷àëüíîé ôàçû j
i
, (ðèñ. 3.4, à). Çíàêîì «+» îáîçíà÷åíî ïîëîæè-
òåëüíîå íàïðàâëåíèå âåùåñòâåííîé îñè, à j =
-
1
$ ïîëîæèòåëü-
íîå íàïðàâëåíèå ìíèìîé îñè. Áóäåì âðàùàòü ýòîò âåêòîð â ïîëî-
æèòåëüíîì íàïðàâëåíèè (ïðîòèâ ÷àñîâîé ñòðåëêè) ñ óãëîâîé ÷àñ-
òîòîé w. Òîãäà â ëþáîé ìîìåíò âðåìåíè ïîëîæåíèå âðàùàþùåãîñÿ
âåêòîðà îïðåäåëèòñÿ êîìïëåêñíîé âåëè÷èíîé (êîìïëåêñíûì ãàðìî-
íè÷åñêèì êîëåáàíèåì):
()
w+j
==w+j+w+j
()
cos()sin()
i
jt
mmimi
iIeItjIt
t
(3.13)
Ïåðâàÿ ÷àñòü ñëàãàåìîãî (3.13) îòðàæàåò ïðîåêöèþ âðàùàþùåãî-
ñÿ âåêòîðà íà âåùåñòâåííóþ îñü, à âòîðàÿ ÷àñòü $ íà ìíèìóþ
îñü. Ñðàâíèâ âòîðîå ñëàãàåìîå â (3.13) ñ (3.6), ïðèõîäèì ê âû-
âîäó: ñèíóñîèäàëüíûé òîê i íà êîìïëåêñíîé ïëîñêîñòè ïðåäñòàâ-
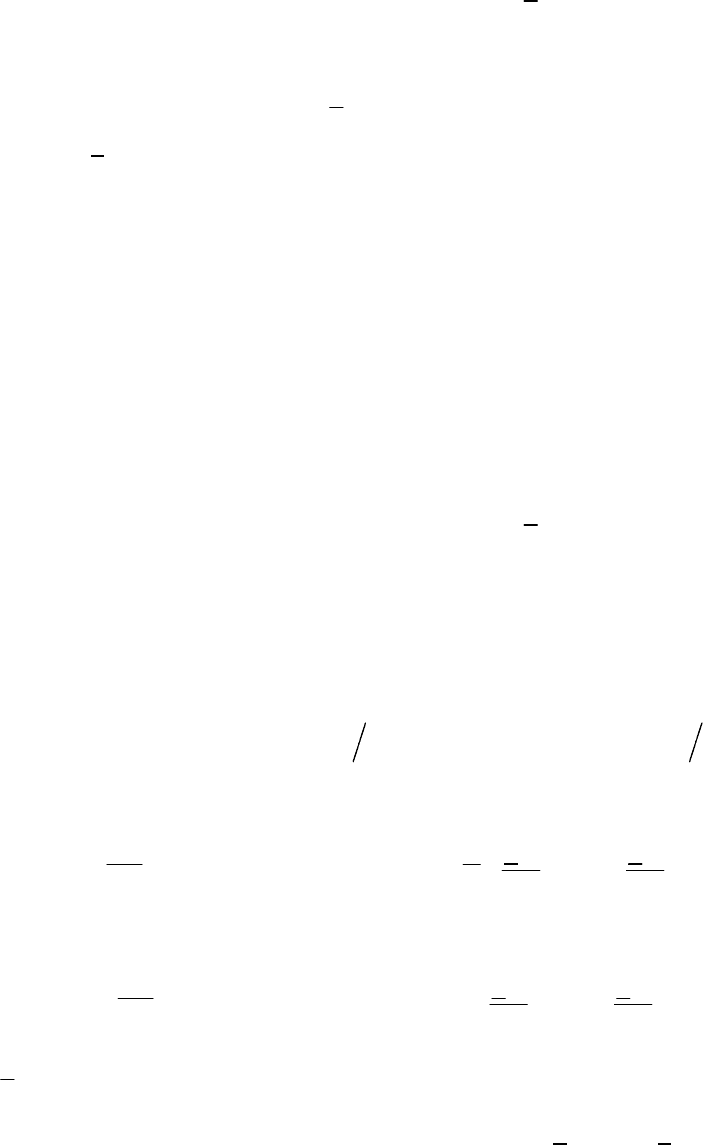
77
ëÿåòñÿ â ôîðìå ïðîåêöèè íà ìíèìóþ îñü âðàùàþùåãîñÿ âåêòîðà
(3.13)
w+j
w
éù
éù
==
ëû
ëû
()
ImIm
i
jt
jt
m
m
i
Ie
Ie
, (3.14)
ãäå Im $ ñîêðàùåííîå îáîçíà÷åíèå ñëîâà Imaginarins (ìíèìûé);
j
=
i
j
m
m
IIe
. (3.15)
Âåëè÷èíà I
m
íîñèò íàçâàíèå êîìïëåêñíîé àìïëèòóäû òîêà.
Âàæíûì ñâîéñòâîì êîìïëåêñíîé àìïëèòóäû ÿâëÿåòñÿ òî, ÷òî
îíà ïîëíîñòüþ îïðåäåëÿåò ãàðìîíè÷åñêîå êîëåáàíèå çàäàííîé ÷àñ-
òîòû w, òàê êàê ñîäåðæèò èíôîðìàöèþ îá åãî àìïëèòóäå è íà-
÷àëüíîé ôàçå.
Åñëè ãàðìîíè÷åñêîå êîëåáàíèå çàäàåòñÿ â ôîðìå êîñèíóñîèäû,
íàïðèìåð
=w+j
cos()
mi
iIt, (3.16)
òî íà êîìïëåêñíîé ïëîñêîñòè ýòîìó òîêó ñîîòâåòñòâóåò ïðîåêöèÿ
âåêòîðà (3.13) íà âåùåñòâåííóþ îñü:
w+j
w
éù
éù
==
ëû
ëû
()
ReRe
i
jt
jt
m
m
i
Ie
Ie
, (3.17)
ãäå Re $ ñîêðàùåííîå îáîçíà÷åíèå ñëîâà Realis (äåéñòâèòåëüíûé,
âåùåñòâåííûé).
Âîçìîæíà è äðóãàÿ ôîðìà ïðåäñòàâëåíèÿ ãàðìîíè÷åñêèõ êîëå-
áàíèé íà êîìïëåêñíîé ïëîñêîñòè. Ó÷òåì, ÷òî ñîãëàñíî ôîðìóëàì
Ýéëåðà
j-jj-j
j=+j=-
cos()2;sin()2
iiii
jjjj
ii
eeeej
. (3.18)
Òîãäà óðàâíåíèå äëÿ òîêà i èç (3.6) ìîæíî çàïèñàòü â âèäå
w+j-w+j
w-w
éù
==
éù
-
ëû
-
êú
ëû
*
()()
1
2
22
ii
m
jtjt
jtjt
mm
I
II
i
ee
ee
jj
. (3.19)
Àíàëîãè÷íî äëÿ òîêà i èç óðàâíåíèÿ (3.16):
w+j-w+j
w-w
éù
==
éù
+
ëû
+
êú
ëû
*
()()
2
22
ii
m
jtjt
jtjt
mm
I
II
i
ee
ee
, (3.20)
ãäå
-j
=
*
i
j
m
m
IIe $ ñîïðÿæåííàÿ êîìïëåêñíàÿ àìïëèòóäà òîêà.
Òàêèì îáðàçîì, òîê i èç (3.6) ñîãëàñíî (3.19) ìîæíî ïðåäñòà-
âèòü êàê ãåîìåòðè÷åñêóþ ðàçíîñòü âåêòîðîâ I
m
/2 è I
m
*/2, âðàùàþ-
ùèõñÿ â ïðîòèâîïîëîæíûõ íàïðàâëåíèÿõ ñ óãëîâîé ÷àñòîòîé w, à
òîê èç (3.16) $ êàê ãåîìåòðè÷åñêóþ ñóììó ýòèõ âåêòîðîâ
(ðèñ. 3.4, á).  ïåðâîì ñëó÷àå i ðàñïîëàãàåòñÿ íà ìíèìîé, à âî
âòîðîì ñëó÷àå $ íà äåéñòâèòåëüíîé îñÿõ. Êîìïëåêñíóþ àìïëèòóäó
ñèíóñîèäàëüíîé ôóíêöèè çàäàííîé ÷àñòîòû ìîæíî ðàññìàòðèâàòü
êàê ïðåîáðàçîâàíèå âðåìåííîé ôóíêöèè â ÷àñòîòíóþ îáëàñòü.

78
w
á
)
a
)
I
m
1
I
m
w
1
0
w
w
1
0
j
1
j
Ðèñ. 3.5
Ñïåêòðàëüíîå (÷àñòîòíîå) ïðåäñòàâëåíèå ãàðìîíè÷åñêèõ êîëå-
áàíèé ñîñòîèò â çàäàíèè àìïëèòóäíîãî è ôàçîâîãî ñïåêòðîâ êîëå-
áàíèÿ (ðèñ. 3.5). Áîëåå ïîäðîáíî ñïåêòðàëüíîå ïðåäñòàâëåíèå è
ìåòîäû àíàëèçà öåïåé, îñíîâàííûå íà ýòîì ïðåäñòàâëåíèè, ðàñ-
ñìîòðåíû â ãë. 5, 9.
3.3. Ãàðìîíè÷åñêèå êîëåáàíèÿ â ðåçèñòèâíûõ,
èíäóêòèâíûõ è åìêîñòíûõ ýëåìåíòàõ
Ðåçèñòèâíûå öåïè. Ïóñòü ê ðåçèñòèâíîìó ýëåìåíòó R ïðèëîæå-
íî ãàðìîíè÷åñêîå íàïðÿæåíèå
(
)
w+j
= sin
u
m
t
uU
. (3.21)
Ñîãëàñíî çàêîíó Îìà ÷åðåç ýëåìåíò R áóäåò ïðîòåêàòü òîê
( ) ( )
w+jw+j
===sinsin
m
ui
m
uU
tt
iI
RR
, (3.22)
ãäå I
m
= U
m
/R $ àìïëèòóäà; j
i
= j
u
$ íà÷àëüíàÿ ôàçà òîêà. Òà-
êèì îáðàçîì, òîê i è íàïðÿæåíèå è â ðåçèñòèâíîì ýëåìåíòå ñîâïà-
äàþò ïî ôàçå äðóã ñ äðóãîì (ðèñ. 3.6, à). Ñðåäíÿÿ çà ïåðèîä Ò
ìîùíîñòü, âûäåëÿåìàÿ â ðåçèñòîðå R,
=====
òò
22
ñð
00
11
TT
PpdtuidtUIIRUG
TT
. (3.23)
Ïðè ïîñëåäîâàòåëüíîì èëè ïàðàëëåëüíîì ñîåäèíåíèÿõ íåñêîëü-
êèõ ðåçèñòèâíûõ ýëåìåíòîâ òîê â öåïè îïðåäåëÿåòñÿ óðàâíåíèåì,
àíàëîãè÷íûì (3.22), ãäå R îïðåäåëÿåòñÿ ñîãëàñíî (1.22) äëÿ ïî-
ñëåäîâàòåëüíîãî è (1.27) äëÿ ïàðàëëåëüíîãî ñîåäèíåíèé ýëåìåíòîâ.
Ïðè ýòîì ôàçîâûé ñäâèã ìåæäó òîêîì è ïðèëîæåííûì íà-
ïðÿæåíèåì îñòàåòñÿ ðàâíûì íóëþ.
Èíäóêòèâíûå öåïè. Ïîä äåéñòâèåì íàïðÿæåíèÿ (3.21) â èíäóê-
òèâíîì ýëåìåíòå áóäåò ïðîòåêàòü òîê ñîãëàñíî (1.9):
( )
p
æö
w+j
===
w+j-
ç÷
w
èø
ò
11
sinsin
2
i
mm
u
t
iudtUI
t
LL
, (3.24)

79
j
I
m
j
t
0
t
j
0
á
)
a
)
U
m
j
i
=
j
u
j
i
j
u
U
m
I
m
j
t
j
0
â
)
j
i
j
u
U
m
I
m
Ðèñ.3.6
ãäå I
m
= U
m
/(wL) = U
m
/X
L
; X
L
= wL $ èíäóêòèâíîå ñîïðîòèâ-
ëåíèå; j
i
= j
u
$ p/2 $ íà÷àëüíàÿ ôàçà òîêà.
Âåëè÷èíó, îáðàòíóþ X
L
, íàçûâàþò èíäóêòèâíîé ïðîâîäèìîñòüþ
B
L
= 1/(wL). Êàê ñëåäóåò èç ïîëó÷åííûõ âûðàæåíèé, òîê â èíäóê-
òèâíîñòè îòñòàåò îò ïðèëîæåííîãî íàïðÿæåíèÿ íà p/2, ò. å. ôàçî-
âûé ñäâèã ìåæäó òîêîì i è íàïðÿæåíèåì è (ðèñ. 3.6, á)
j=j-j=p
2
ui
. (3.25)
Íà âåêòîðíîé äèàãðàììå ôàçîâûé ñäâèã j îòêëàäûâàåòñÿ îò âåê-
òîðà òîêà ê âåêòîðó íàïðÿæåíèÿ. Íåòðóäíî âèäåòü, ÷òî ñðåäíÿÿ çà
ïåðèîä ìîùíîñòü â èíäóêòèâíîì ýëåìåíòå ðàâíà íóëþ.
Ïðè ïîñëåäîâàòåëüíîì è ïàðàëëåëüíîì ñîåäèíåíèÿõ èíäóêòèâ-
íûõ ýëåìåíòîâ òîê â öåïè îïðåäåëÿåòñÿ óðàâíåíèåì, àíàëîãè÷íûì
(3.24), ãäå L íàõîäèòñÿ ñîãëàñíî (1.23) äëÿ ïîñëåäîâàòåëüíîãî è
(1.29) äëÿ ïàðàëëåëüíîãî ñîåäèíåíèé.
Åìêîñòíûå öåïè. Äëÿ åìêîñòíîãî ýëåìåíòà ñîãëàñíî óðàâíåíèþ
(1.12) èìååì:
( )
p
æö
w+j
==w=
w+j+
ç÷
èø
sinsin
2
i
mm
u
du
t
iCCUI
t
dt
, (3.26)
ãäå I
m
= wCU
m
=
B
C
U
m
; B
C
= wC $ åìêîñòíàÿ ïðîâîäèìîñòü; j
i
=
= j
u
+ p/2 $ íà÷àëüíàÿ ôàçà òîêà. Âåëè÷èíó, îáðàòíóþ B
C
, íàçû-
âàþò åìêîñòíûì ñîïðîòèâëåíèåì X
C
= 1/(wC). Ôàçîâûé ñäâèã
ìåæäó òîêîì è íàïðÿæåíèåì íà åìêîñòíîì ýëåìåíòå
j=j-j=-p
2
ui
. (3.27)
Èç ïðèâåäåííûõ óðàâíåíèé ñëåäóåò, ÷òî òîê â åìêîñòè îïåðå-
æàåò ïðèëîæåííîå íàïðÿæåíèå íà óãîë p/2 (ðèñ. 3.6, â), ïðè÷åì
çíàê «$» ñâèäåòåëüñòâóåò îá îòñòàâàíèè íàïðÿæåíèÿ è îò òîêà i.
Ñðåäíÿÿ çà ïåðèîä ìîùíîñòü â åìêîñòíîé öåïè òàêæå ðàâíà íóëþ.
Ïðè ïîñëåäîâàòåëüíîì è ïàðàëëåëüíîì ñîåäèíåíèÿõ åìêîñòíûõ
ýëåìåíòîâ òîê â öåïè îïðåäåëÿåòñÿ ñîãëàñíî (3.26), ãäå Ñ íàõî-
äèòñÿ èç (1.24) äëÿ ïîñëåäîâàòåëüíîãî è (1.28) äëÿ ïàðàëëåëüíîãî
ñîåäèíåíèé.
80
u
L
u
R
u
C
u
i
L
C
j
+
j
0
j
i
j
u
U
m
I
m
U
m
C
U
m
L
U
m
R
=U
m
a
U
m
L
-U=U
mm
C
p
Ðèñ. 3.7 Ðèñ. 3.8
3.4. Ãàðìîíè÷åñêèå êîëåáàíèÿ â öåïè ïðè ïîñëåäîâàòåëüíîì
ñîåäèíåíèè R, L, Ñ-ýëåìåíòîâ
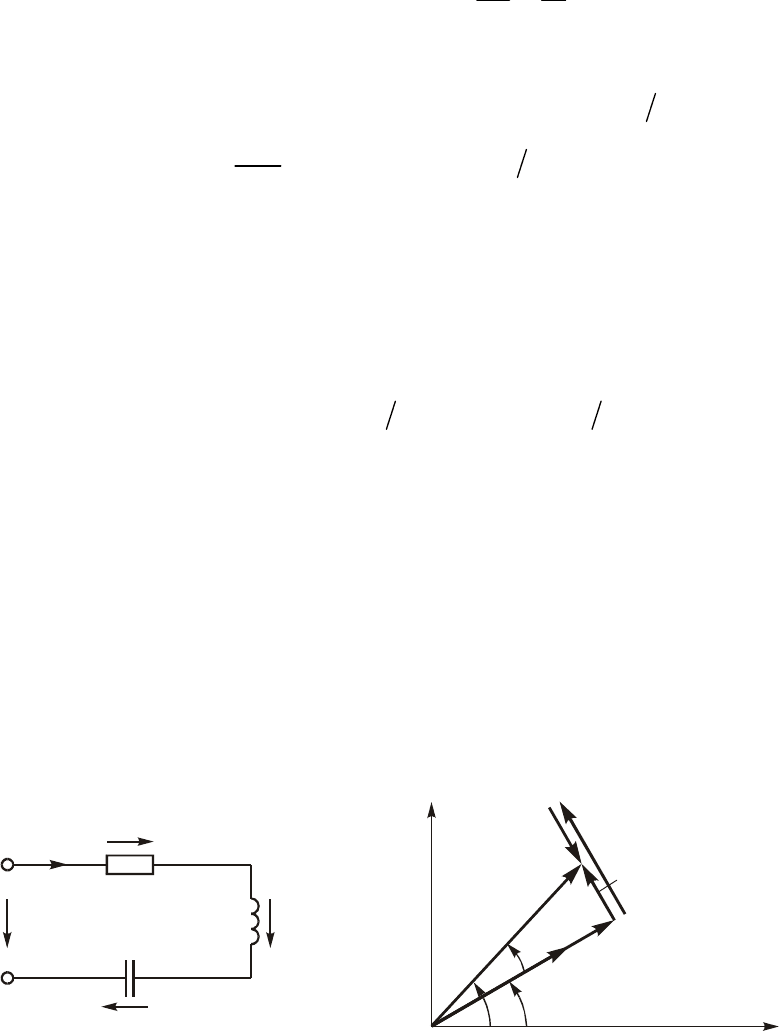
Äîïóñòèì, ÷òî â öåïè, ñîäåðæàùåé ïîñëåäîâàòåëüíî ñîåäèíåí-
íûå ýëåìåíòû R, L, Ñ (ðèñ. 3.7), ïðîòåêàåò òîê
(
)
w+j
= sin
i
m
t
iI . (3.28)
Ñîãëàñíî ÇÍÊ íàïðÿæåíèå íà îòäåëüíûõ ó÷àñòêàõ öåïè îïðåäå-
ëÿåòñÿ óðàâíåíèåì
=++=++
ò
1
RLC
di
uuuuRiLidt
dtC
. (3.29)
Ïîäñòàâèâ â (3.29) çíà÷åíèå òîêà èç (3.28), ïîëó÷èì
(
)
(
)
( )
w+jw+j-p
=+w+
w+j+p
+
w
2
sinsin
1
2
sin,
ii
mm
i
m
tt
uRILI
t
I
C
èëè
(
)
(
)
( )
=++
w+j
w+j
+
w+j
sinsin
sin,
mRmL
R
L
mC
C
uUU
t
t
U
t
(3.30)
ãäå
===
ü
ý
j=jj=j-pj=j+p
þ
;;;
;2;2.
mRmmLLmmCCm
RiLiCi
URIUXIUXI
(3.31)
Íà ðèñ. 3.8 èçîáðàæåíà âåêòîðíàÿ äèàãðàììà íàïðÿæåíèé, îïè-
ñûâàåìûõ óðàâíåíèé (3.30).
Íàïðÿæåíèå U
mR
íà ðåçèñòèâíîì ñîïðîòèâëåíèè R íàçûâàåòñÿ
àêòèâíîé ñîñòàâëÿþùåé ïðèëîæåííîãî íàïðÿæåíèÿ è îáîçíà÷à-
åòñÿ U
ma
= U
mR
, ðàçíîñòü íàïðÿæåíèé U
mp
= U
mL
U
mC
íàçûâà-
åòñÿ ðåàêòèâíîé ñîñòàâëÿþùåé. Ñîãëàñíî ýòîìó îïðåäåëåíèþ è
ôîðìóëàì (3.31) èìååì:
(
)
===
-
ap
;
mmmmm
LC
URIUIXI
XX
. (3.32)
