Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.

41
b
R
ã
u
ã
+
à
)
G
ã
á
)
a
b
a
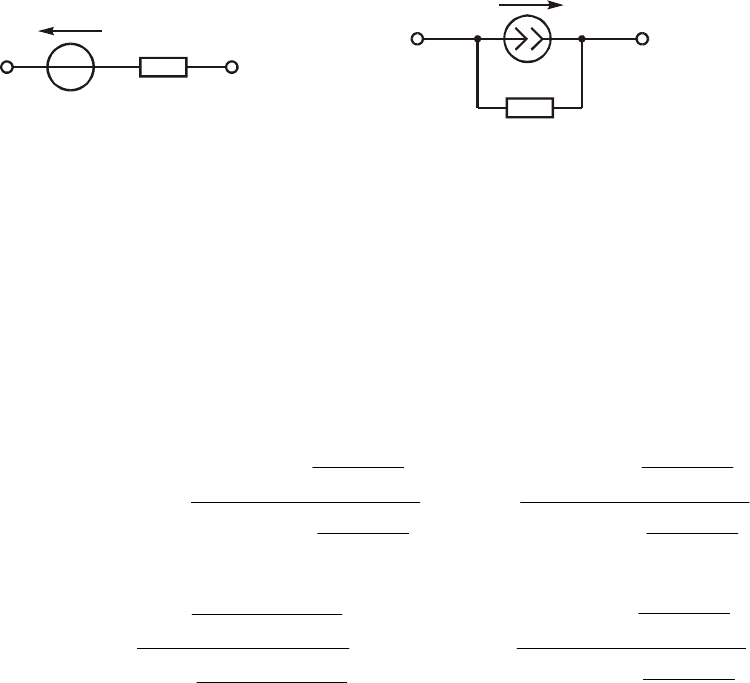
Ðèñ. 1.26
8. Äàòü îïðåäåëåíèÿ ãðàôà, óçëà, âåòâè, äåðåâà, êîíòóðà ýëåêòðè-
÷åñêîé öåïè.
9. Äàòü îïðåäåëåíèÿ I è II çàêîíîâ Êèðõãîôà äëÿ ýëåêòðè÷åñêîé
öåïè. Êàê îíè çàïèñûâàþòñÿ â ìàòðè÷íîé ôîðìå?
10. Îïðåäåëèòü ýêâèâàëåíòíîå ñîïðîòèâëåíèå öåïè, èçîáðàæåííîé
íà ðèñ. 1.24, îòíîñèòåëüíî òî÷åê ab, cd, db, ad.
Îòâåò:
45
3
2
45
1
45
23
45
ab
RR
R
R
RR
RR
RR
RR
RR
æö
+
×
ç÷
+
èø
=+
++
+
;
45
2
3
45
45
32
45
cd
RR
R
R
RR
R
RR
RR
RR
æö
+
×
ç÷
+
èø
=
++
+
;
(
)
( )
4
23
5
423
4
23
5
423
db
R
RR
R
RRR
R
R
RR
R
RRR
+
×
++
=
+
+
++
;
45
2
3
45
1
45
32
45
ad
RR
R
R
RR
RR
RR
RR
RR
æö
+
×
ç÷
+
èø
=+
++
+
.
11. Ñîñòàâèòü áàëàíñ ìîùíîñòè äëÿ öåïè, èçîáðàæåííîé íà
ðèñ. 1.25.
Îòâåò:
èñò ã1134 ã
puiui
=×+×
;
2222
ïîòð11223344
pRiRiRiRi
=+++;
èñòïîòð
pp
=
.
12. Îïðåäåëèòü ïàðàìåòðû èñòî÷íèêà òîêà, èçîáðàæåííîãî íà
ðèñ. 1.26, á, ýêâèâàëåíòíîãî çàäàííîìó èñòî÷íèêó íàïðÿæåíèÿ,
åñëè U
ã
= 100 Â, R
ã
= 2 Îì.
Îòâåò: i
ã
= 50 À; G
ã
= 0,5 Îì
-1
.
ÃËÀÂÀ 2. ËÈÍÅÉÍÛÅ ÝËÅÊÒÐÈ×ÅÑÊÈÅ ÖÅÏÈ
 ÐÅÆÈÌÅ ÏÎÑÒÎßÍÍÎÃÎ ÒÎÊÀ
2.1. Ìåòîä çàêîíîâ Êèðõãîôà
 ýëåêòðè÷åñêèõ öåïÿõ, ñîäåðæàùèõ àêòèâíûå ýëåìåíòû (ýëåê-
òðîííûå ëàìïû, òðàíçèñòîðû, îïåðàöèîííûå óñèëèòåëè è äðóãèå
çàâèñèìûå èñòî÷íèêè) âàæíûì ðåæèìîì ðàáîòû ÿâëÿåòñÿ ñòàòè-
÷åñêèé.  ñòàòè÷åñêîì ðåæèìå íà ýëåêòðîäû àêòèâíîãî ýëåìåíòà
ïîäàþòñÿ ïîñòîÿííûå òîêè è íàïðÿæåíèÿ, îáåñïå÷èâàþùèå çàäàí-
íûå óñëîâèÿ ðàáîòû òîãî èëè èíîãî óñòðîéñòâà. Ñòàòè÷åñêèé ðå-
42
æèì õàðàêòåðèçóåòñÿ çàâèñèìîñòÿìè ìåæäó ïîñòîÿííûìè òîêàìè è
íàïðÿæåíèÿìè â îòäåëüíûõ ÷àñòÿõ ýëåêòðè÷åñêîé öåïè è ÿâëÿåòñÿ
îäíèì èç îñíîâíûõ ðåæèìîâ ðàáîòû ëþáîãî ýëåêòðè÷åñêîãî óñò-
ðîéñòâà. Ïîýòîìó àíàëèç öåïåé â ðåæèìå ïîñòîÿííîãî òîêà èãðàåò
âàæíóþ ðîëü â îáùåé òåîðèè ýëåêòðè÷åñêîé ñâÿçè.
Êàê îòìå÷àëîñü â § 1.2 ïðè ïîñòîÿííîì òîêå è íàïðÿæåíèè èí-
äóêòèâíîñòü ýêâèâàëåíòíà êîðîòêîçàìêíóòîìó ó÷àñòêó (ðèñ. 1.1, à),
åìêîñòü $ ðàçðûâó öåïè. Òàêèì îáðàçîì, â ðåæèìå ïîñòîÿííîãî
òîêà â ìîäåëè öåïè áóäóò îòñóòñòâîâàòü ðåàêòèâíûå ýëåìåíòû, è
îíà ïðèîáðåòåò ÷èñòî ðåçèñòèâíûé õàðàêòåð. Ëèíåéíûå ðåçèñòèâ-
íûå öåïè ïîëíîñòüþ îïèñûâàþòñÿ ñèñòåìîé ëèíåéíûõ àëãåáðàè÷å-
ñêèõ óðàâíåíèé, ñîñòàâëÿåìûõ íà îñíîâàíèè çàêîíà Êèðõãîôà. Â
ýòîé ãëàâå ðàññìîòðèì îñíîâíûå ìåòîäû àíàëèçà ëèíåéíûõ ðåçè-
ñòèâíûõ öåïåé, íàõîäÿùèõñÿ ïîä âîçäåéñòâèåì ïîñòîÿííûõ òîêîâ è
íàïðÿæåíèé. Ïîñòîÿííûå òîêè è íàïðÿæåíèÿ â äàëüíåéøåì áóäåì
îáîçíà÷àòü ïðîïèñíûìè áóêâàìè I è U ñîîòâåòñòâåííî.
Ìåòîä ðàñ÷åòà ýëåêòðè÷åñêèõ öåïåé, îñíîâàííûé íà çàêîíàõ
Êèðõãîôà, â êîòîðûõ íåçàâèñèìûìè ïåðåìåííûìè ÿâëÿþòñÿ òîêè â
âåòâÿõ, íàçûâàþò ìåòîäîì òîêîâ âåòâåé. Â ñîîòâåòñòâèè ñ ýòèì
ìåòîäîì äëÿ íàõîæäåíèÿ òîêîâ èëè íàïðÿæåíèé âåòâåé ñîñòàâëÿ-
þòñÿ (nó
$ 1) óðàâíåíèé (1.16) ïî ÇÒÊ è (n
â
$ n
ó
+ 1) óðàâíåíèé
(1.17) ïî ÇÍÊ.  ðåçóëüòàòå ïîëó÷àåì ñèñòåìó èç (n
ó
$ 1) + (n
â
$
$ n
ó
+ 1) = n
â
ëèíåéíî-íåçàâèñèìûõ óðàâíåíèé, ÷èñëî êîòîðûõ
ðàâíî ÷èñëó òîêîâ âåòâåé. Ñîâìåñòíîå ðåøåíèå ýòîé ñèñòåìû ïî-
çâîëÿåò íàéòè âñå òîêè.
Ïðè âûáîðå íåçàâèñèìûõ êîíòóðîâ íåîáõîäèìî ðóêîâîäñòâî-
âàòüñÿ òîïîëîãèåé ýëåêòðè÷åñêîé öåïè (§ 1.3): ñîñòàâèòü ãðàô öå-
ïè, âûáðàòü äåðåâî, äîïîëíèòü åãî õîðäîé, ïðè ýòîì îáðàçóåòñÿ
êîíòóð. Ïóòåì ïîñëåäîâàòåëüíîãî äîïîëíåíèÿ õîðäàìè äåðåâà äî
èñõîäíîãî ãðàôà ïîëó÷àåì (n
â
$ n
ó
+ 1) íåçàâèñèìûõ êîíòóðîâ.
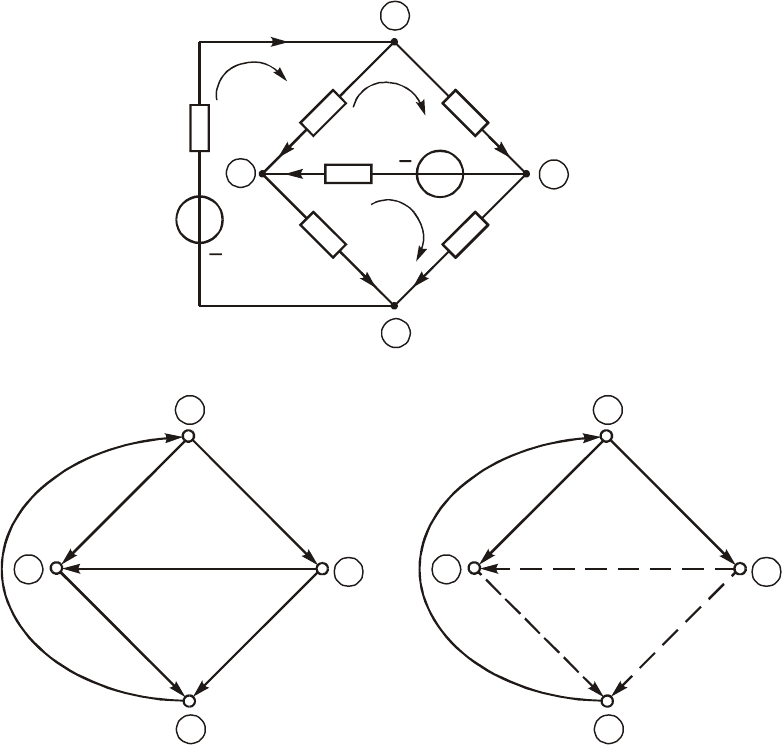
Ïðèìåð. Ðàññ÷èòàòü òîêè âåòâåé ñõåìû ðåçèñòèâíîé öåïè, èçîáðàæåííîé
íà ðèñ. 2.1. à ïî ìåòîäó óðàâíåíèé Êèðõãîôà.
Ïîñòðîèì ãðàô öåïè (ðèñ. 2.1, á) è âûáåðåì äåðåâî (ðèñ. 2.1, â). Äîïîë-
íèì äåðåâî õîðäàìè 2, 5, 6 (íà ðèñ. 2.1, â ïîêàçàíî ïóíêòèðîì). Â ðåçóëüòàòå
îáðàçóåòñÿ òðè íåçàâèñèìûõ êîíòóðà I, II, III (ðèñ. 2.1, à). Ñîñòàâèì óðàâíå-
íèå ïî ÇÒÊ è ÇÍÊ.
Ñõåìà èìååò n
y
= 4 óçëà, n
â
= 6 âåòâåé. Âûáåðåì óçåë 4 â êà÷åñòâå áàçèñ-
íîãî è ñîñòàâèì n
y
= 3 óðàâíåíèÿ ïî ÇÒÊ:
134
235
246
äëÿ óçëà 0,
äëÿ óçëà 0,
äëÿ óçëà 0.
1III
2III
3III
-++=
ü
ï
--+=
ý
ï
-+=
þ
(2.1)
Ïî ÇÍÊ ñîñòàâëÿåì n
â
$ n
ó
+ 1 = 3 óðàâíåíèÿ äëÿ êîíòóðîâ, ïîêàçàííûõ
íà ðèñ. 2.1, à ñòðåëêàìè: äëÿ êîíòóðà I $U
ã1
+ U
1
+ U
3
+ U
5
= 0; äëÿ êîíòóðà
II + U
ã2
+ U
2
$ U
3
+ U
4
= 0; äëÿ êîíòóðà III $U
ã2
$ U
2
+ U
6
$ U
5
= 0. Èëè
ñ ó÷åòîì çàêîíà Îìà (1.6):
43
R
2
R
4
III
I
U
ã
2
+
R
6
II
1
2
3
4
à
)
R
5
R
3
I
4
I
2
I
3
I
5
I
6
U
ã
1
R
1
I
1
1
2
3
4
1
2
34
56
á
)
1
2
3
4
1
2
3
4
5
6
â
)
+
Ðèñ. 2.1
ã1113355
ã2223344
ã2226655
0,
0,
0.
URIRIRI
URIRIRI
URIRIRI
ü
-+++=
ï
+-+=
ý
ï
--+-=
þ
(2.2)
Ðåøàÿ ñîâìåñòíî ñèñòåìû óðàâíåíèé (2.1) è (2.2), íàéäåì èñêîìûå òîêè.
Ïðè èñïîëüçîâàíèè çàêîíîâ Êèðõãîôà â êà÷åñòâå íåçàâèñèìûõ
ïåðåìåííûõ ìîæíî áûëî âçÿòü íàïðÿæåíèÿ âåòâåé (ìåòîä íàïðÿ-
æåíèÿ âåòâåé) èëè òîêè îäíèõ âåòâåé è íàïðÿæåíèÿ äðóãèõ (ãèá-
ðèäíûé ìåòîä).
 ñëó÷àå, åñëè â öåïè èìååòñÿ âåòâü ñ èñòî÷íèêîì òîêà, òî íå-
èçâåñòíûì ïàðàìåòðîì â ýòîé âåòâè ÿâëÿåòñÿ íàïðÿæåíèå íà çàæèìàõ
èñòî÷íèêà, êîòîðîå ìîæíî íàéòè ìåòîäîì íàïðÿæåíèÿ âåòâåé.
2.2. Ïðåîáðàçîâàíèå ðåçèñòèâíûõ ýëåêòðè÷åñêèõ öåïåé
 ñëó÷àå, êîãäà íà öåïü âîçäåéñòâóåò îäèí èñòî÷íèê ïîñòîÿí-
íîãî íàïðÿæåíèÿ èëè òîêà, íàèáîëåå ýôôåêòèâíûì ÿâëÿåòñÿ ìåòîä
44
R
2
R
4
1
2
à
)
R
5
R
3
I
4
I
2
I
3
I
5
R
1
I
1
3
4
5
0
I
4
I
5
I
1
I
2
I
3
I
34
I
45
I
51
I
12
I
23
R
34
R
45
R
51
R
23
R
12
á
)
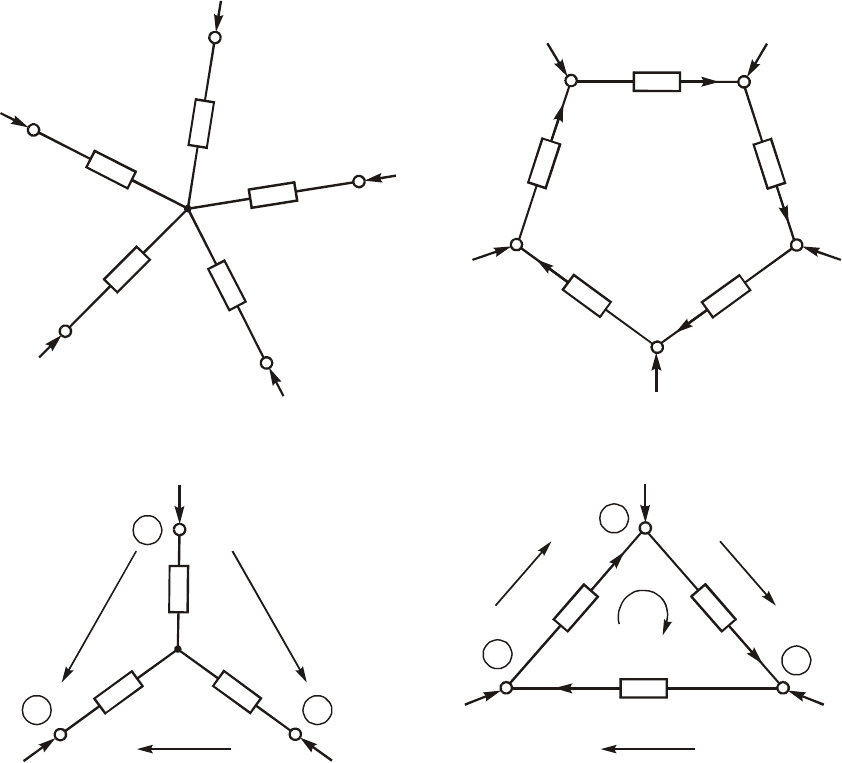
Ðèñ. 2.2
U
31
I
3
I
2
I
3
R
2
R
3
a
)
I
1
I
2
I
12
R
12
I
31
I
23
R
31
R
23
I
1
R
1
1
23
U
23
U
12
U
23
1
3
2
U
12
á
)
U
31
I
Ðèñ. 2.3
ïðåîáðàçîâàíèÿ ýëåêòðè÷åñêèõ öåïåé. Ñóòü ýòîãî ìåòîäà çà-
êëþ÷àåòñÿ â íàõîæäåíèè ýêâèâàëåíòíîãî ñîïðîòèâëåíèÿ öåïè îòíî-
ñèòåëüíî çàæèìîâ (ïîëþñîâ) èñòî÷íèêà.
 § 1.5 áûëè ðàññìîòðåíû ïðîñòåéøèå ìåòîäû ïðåîáðàçîâàíèÿ
ïîñëåäîâàòåëüíîãî è ïàðàëëåëüíîãî ñîåäèíåííûõ ïàññèâíûõ ýëå-
ìåíòîâ (ñì. ôîðìóëû (1.22)$ (1.24) è (1.27) $ (1.29)). Îäíàêî íà
ïðàêòèêå âñòðå÷àþòñÿ áîëåå ñëîæíûå ñîåäèíåíèÿ ýëåìåíòîâ, êî-
òîðûå íåëüçÿ ñâåñòè òîëüêî ê ïîñëåäîâàòåëüíîìó èëè ïàðàëëåëü-
íîìó. Ïðèìåðîì ïîäîáíîãî ñîåäèíåíèÿ ÿâëÿþòñÿ ñîåäèíåíèÿ ìíî-
ãîëó÷åâîé çâåçäîé (ðèñ. 2.2, à) è ìíîãîóãîëüíèêîì (ðèñ. 2.2, á).
Õàðàêòåðíîé îñîáåííîñòüþ ýòèõ ñîåäèíåíèé ÿâëÿåòñÿ íàëè÷èå
âíóòðåííåãî óçëà 0 â çâåçäå è âíóòðåííåãî êîíòóðà â ìíîãîóãîëü-
íèêå. Íàèáîëåå ÷àñòî âñòðå÷àþòñÿ ñëó÷àè òðåõëó÷åâîé çâåçäû è
òðåóãîëüíèêà (ðèñ. 2.3, à, á).
Íàéäåì ôîðìóëû ïðåîáðàçîâàíèÿ ñîåäèíåíèÿ «òðåóãîëüíèêà» â
«çâåçäó». Çàïèøåì äëÿ ñõåìû «òðåóãîëüíèê» óðàâíåíèÿ ïî ÇÒÊ è
ÇÍÊ (ðèñ. 2.3, á):

45
12311
23122
122331
äëÿ óçëà 0,
äëÿ óçëà 0,
äëÿ êîíòóðà 0.
1III
2III
IUUU
--=
ü
ï
--=
ý
ï
++=
þ
(2.3)
Ðåøàÿ ñèñòåìó (2.3) îòíîñèòåëüíî U
12
ñ ó÷åòîì ðàâåíñòâ U
23
=
= R
23
I
23
è U
31
= R
31
I
31
, ïîëó÷àåì
=-
++++
12312312
1212
122331122331
RRRR
UII
RRRRRR
. (2.4)
Äëÿ ñõåìû «çâåçäà» íà îñíîâàíèè ÇÍÊ äëÿ U
12
ìîæíî çàïèñàòü
(ñì. ðèñ. 2.3, à):
=-
121122
URIRI
. (2.5)
Òàê êàê íà îñíîâàíèè ïðèíöèïà ýêâèâàëåíòíîñòè íàïðÿæåíèå
U
12
è òîêè I
1
è I
2
èç (2.4) è (2.5) ðàâíû äðóã äðóãó, òî ïîïàðíî
ðàâíû è ñîìíîæèòåëè ïðè òîêàõ I
1
è I
2
:
==
++++
12312312
12
122331122331
;
RRRR
RR
RRRRRR
. (2.6)
Óðàâíåíèå äëÿ R
3
ïîëó÷àåì àíàëîãè÷íî (êðóãîâîé çàìåíîé èí-
äåêñîâ):
=
++
3123
3
122331
RR
R
RRR
. (2.7)
Óðàâíåíèÿ (2.6) è (2.7) ïîçâîëÿþò îñóùåñòâèòü ïåðåõîä îò ñî-
åäèíåíèÿ ðåçèñòèâíûõ ýëåìåíòîâ «òðåóãîëüíèê» ê ñîåäèíåíèþ
«çâåçäà». Îáðàòíûé ïåðåõîä ìîæíî ïîëó÷èòü ïî ôîðìóëàì
1212123
2323231
3131312
,
,
,
RRRRRR
RRRRRR
RRRRRR
ü
=++
ï
=++
ý
ï
=++
þ
(2.8)
îñóùåñòâëÿåìûå èç (2.6) è (2.7).
Åñëè âûðàçèòü ñîïðîòèâëåíèå ñòîðîí òðåóãîëüíèêà è ëó÷åé
çâåçäû ÷åðåç ïðîâîäèìîñòè G
12
= 1/R
12
, G
23
= 1/R
23
, G
31
=
= 1/R
31
, G
1
= 1/R
1
, G
2
= 1/R
2
, G
3
= 1/R
3
, òî ôîðìóëû (2.8)
ïðèìóò äóàëüíûé âèä (2.6), (2.7):
=
++
=
++
=
++
12
12
123
23
23
123
31
31
123
,
,
.
GG
G
GGG
GG
G
GGG
GG
G
GGG
(2.9)
46
U
23
R
1
R
3
R
2
R
34
R
24
1
2
3
4
I
24
I
34
U
ã
+
U
12
U
31
U
ã
+
I
34
R
34
I
24
R
24
R
12
R
31
I
12
I
31
I
23
4
2
1
3
U
23
R
23
U
31
U
12
I
a
)
á
)
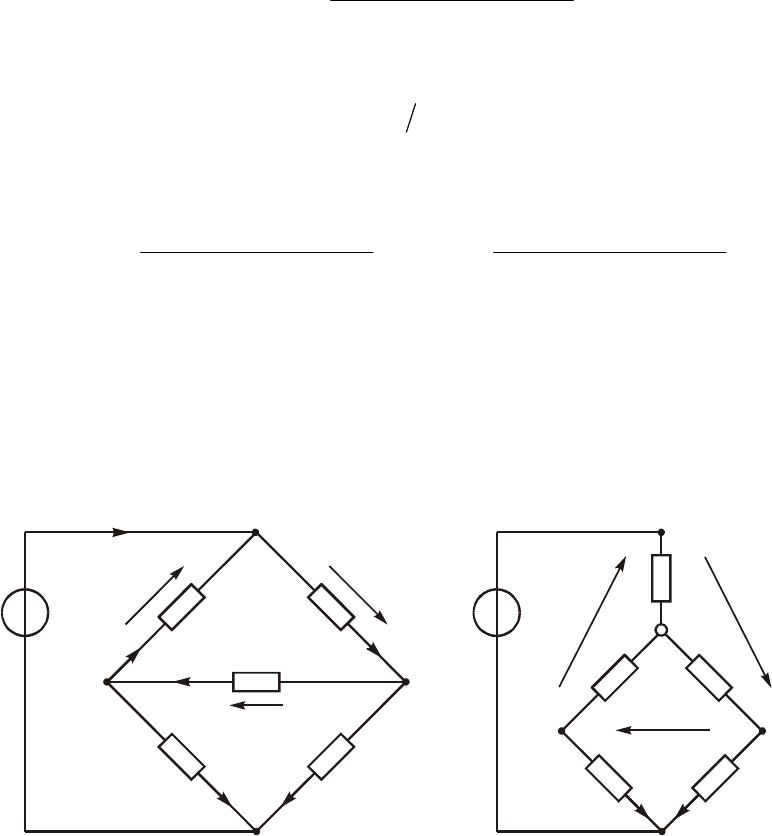
Ðèñ. 2.4
Ïðèìåð. Ðàññ÷èòàòü òîêè âåòâåé ñõåìû ðåçèñòèâíîé öåïè, èçîáðàæåííîé
íà ðèñ. 2.4, à. Äàííàÿ ñõåìà ìîæåò ñëóæèòü ìîäåëüþ èçìåðèòåëüíîãî ìîñòà,
êîòîðûé íàõîäèò øèðîêîå ïðèìåíåíèå â ðàçëè÷íûõ èçìåðèòåëüíûõ ïðèáîðàõ,
â ÷àñòíîñòè äëÿ èçìåðåíèÿ ñîïðîòèâëåíèé. Ïðèíöèï ðàáîòû ìîñòà îñíîâàí íà
âûïîëíåíèè óñëîâèé áàëàíñà åãî ïëå÷åé.
=
31241234
RRRR
.
Ïðè ýòîì ïîòåíöèàëû óçëîâ 2 è 3 îêàçûâàþòñÿ îäèíàêîâûìè è â äèàãîíàëè
ìîñòà R
23
òîê áóäåò ðàâåí íóëþ. Òàêèì îáðàçîì, åñëè âêëþ÷èòü â äèàãîíàëü
ìîñòà âìåñòî R
23
èçìåðèòåëüíûé ïðèáîð $ àìïåðìåòð, òî ïóòåì èçìåíåíèÿ îä-
íîãî èç ñîïðîòèâëåíèé ïëå÷à (íàïðèìåð, R
24
ñ ïîìîùüþ ìàãàçèíà ñîïðîòèâëå-
íèé), ìîæíî íàéòè ñîïðîòèâëåíèå äðóãîãî (íàïðèìåð R
31
). Äëÿ ñëó÷àÿ, êîãäà
R
12
= R
31
= R, óñëîâèå áàëàíñà äîñòèãàåòñÿ ïðè R
34
= R
24
.
Ïðåîáðàçóåì òðåóãîëüíèê R
12
, R
23
,
R
31
â çâåçäó ñ ëó÷àìè R
1
, R
2
,
R
3
(ðèñ. 2.4, á), ãäå R
1
, R
2
,
R
3
îïðåäåëÿþòñÿ ôîðìóëàìè (2.6) è (2.7). Òîãäà ýê-
âèâàëåíòíîå ñîïðîòèâëåíèå öåïè îòíîñèòåëüíî çàæèìîâ èñòî÷íèêà (óçëû 1 è 4)
++
=+
+++
334224
ý1
334224
()()
RRRR
RR
RRRR
.
Òîê èñòî÷íèêà îïðåäåëÿåì ïî çàêîíó Îìà:
=
ã ý
IUR
,
à òîêè âåòâåé I
34
è I
24
ïî «ôîðìóëå ðàçáðîñà», êîòîðàÿ ìîæåò áûòü ïîëó÷åíà
íà îñíîâàíèè ÇÒÊ è çàêîíà Îìà äëÿ ñîïðîòèâëåíèé (R
3
+ R
34
) è (R
2
+ R
24
):
++
==
++++++
224334
3424
224334224334
;
RRRR
IIII
RRRRRRRR
.
Äëÿ íàõîæäåíèÿ òîêîâ I
12
è I
31
îïðåäåëèì íàïðÿæåíèå U
12
äëÿ ïðåîáðàçî-
âàííîé ñõåìû (ðèñ. 2.4, á): U
12
= R
1
I + R
2
I
24
. Ó÷èòûâàÿ, ÷òî U
12
â ñõåìå
òðåóãîëüíèêà (ðèñ. 2.4, à) è â ñõåìå çâåçäû (ðèñ. 2.4, á) ðàâíû ñîãëàñíî
ïðèíöèïà ýêâèâàëåíòíîñòè, íàéäåì òîê I
12
= U
12
/R
12
. Òîêè I
23
è I
31
îïðåäå-
ëÿåì ïî ÇÒÊ: I
23
= I
12
$ I
24
; I
31
= I
23
$ I
34
.
47
U
ã
1
+
U
ã
2
+
R
1
R
2
R
3
I
1
I
1
¢
I
2
I
3
a
)
U
ã
1
+
R
3
á
)
R
1
R
2
I
3
¢
I
2
¢
I
1
¢¢
U
ã
2
+
R
3
â
)
R
1
R
2
I
3
¢
¢
I
2
¢
¢
Ðèñ. 2.5
Àíàëîãè÷íî ôîðìóëå (2.9) ìîæíî ïîëó÷èòü ôîðìóëû ïðåîáðà-
çîâàíèÿ n-ëó÷åâîé çâåçäû â ïîëíûé ìíîãîóãîëüíèê ñ ÷èñëîì âåòâåé
ðàâíûì n
â
= n(n $ 1)/2:
=
=
å
â
1
m
l
lm
n
k
k
GG
G
G
. (2.10)
Ñëåäóåò îòìåòèòü, ÷òî îáðàòíàÿ çàäà÷à ïðåîáðàçîâàíèÿ ìíîãî-
óãîëüíèêà â ýêâèâàëåíòíóþ n-ëó÷åâóþ çâåçäó ïðè n >3 íå èìååò
ðåøåíèÿ, òàê êàê ïðè ýòîì îêàçûâàåòñÿ ÷èñëî óðàâíåíèé n (n $ 1)/2
ïðåâûøàåò ÷èñëî íåèçâåñòíûõ.
2.3. Ìåòîä íàëîæåíèÿ
 îñíîâå ìåòîäà íàëîæåíèÿ ëåæèò ïðèíöèï ñóïåðïîçèöèè (íà-
ëîæåíèÿ), ëèíåéíûõ ýëåêòðè÷åñêèõ öåïåé (§ 1.6). Ýòîò ìåòîä ïðè-
ìåíÿåòñÿ â ñëó÷àå, êîãäà â öåïè äåéñòâóåò íåñêîëüêî èñòî÷íèêîâ
íàïðÿæåíèÿ èëè òîêà. Ïðè ýòîì â ñîîòâåòñòâèè ñ ýòèì ïðèíöèïîì
íàõîäÿò ÷àñòè÷íûå òîêè è íàïðÿæåíèÿ, à ðåçóëüòèðóþùèå ðåàêöèè
îïðåäåëÿþòñÿ ïóòåì àëãåáðàè÷åñêîãî ñóììèðîâàíèÿ ÷àñòè÷íûõ òî-
êîâ è íàïðÿæåíèé.
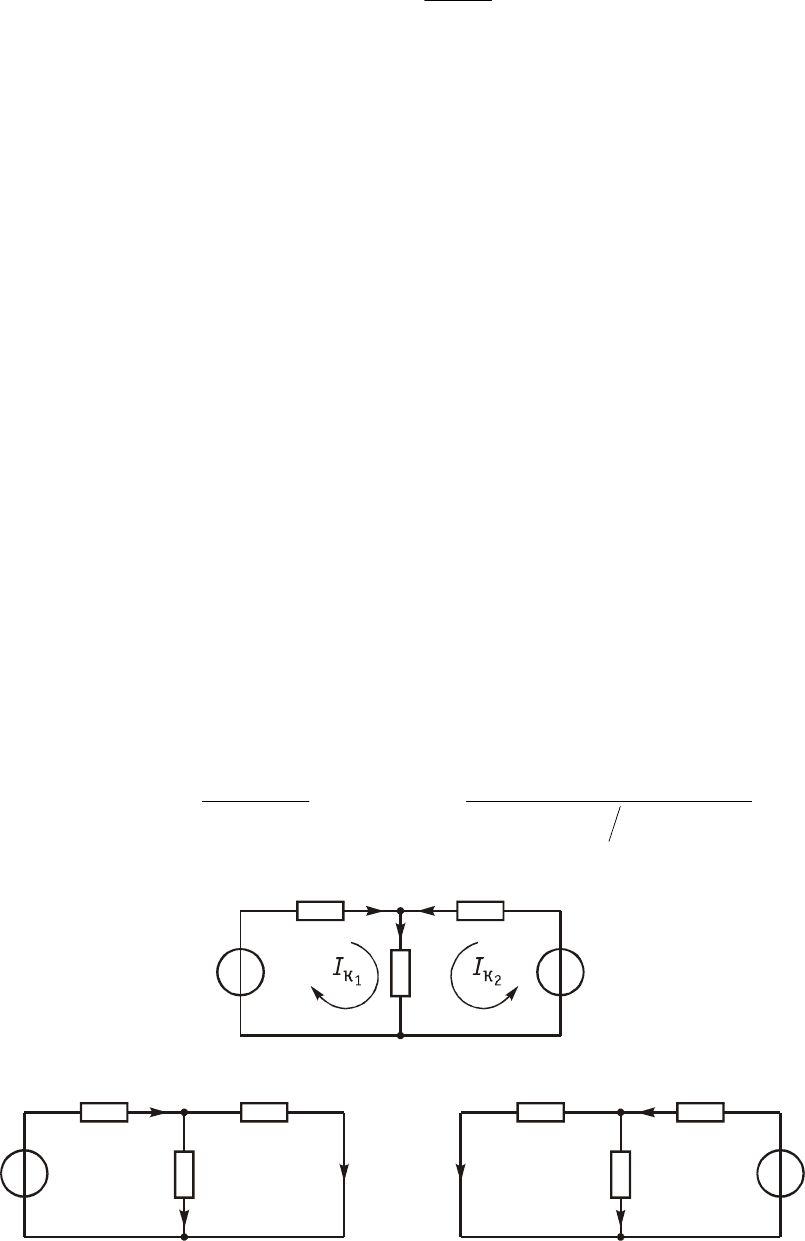
Ïðîèëëþñòðèðóåì ïðèíöèï íàëîæåíèÿ íà ïðèìåðå ðåçèñòèâíîé
öåïè, èçîáðàæåííîé íà ðèñ. 2.5, à, ñîäåðæàùåé èäåàëüíûå èñòî÷-
íèêè íàïðÿæåíèÿ. Íàéäåì òîê â ðåçèñòèâíîì ýëåìåíòå R
3
. Ïîëî-
æèì âíà÷àëå, ÷òî â öåïè äåéñòâóåò òîëüêî îäèí èñòî÷íèê U
ã1
; âòî-
ðîé èñòî÷íèê íàïðÿæåíèÿ èñêëþ÷àåòñÿ è çàæèìû åãî çàêîðà÷èâà-
þòñÿ. Ïðè ýòîì ïîëó÷àåì ÷àñòè÷íóþ ñõåìó, èçîáðàæåííóþ íà
ðèñ. 2.5, á. Îïðåäåëèì òîê I
3
¢
îò âîçäåéñòâèÿ íàïðÿæåíèÿ U
ã1
:
¢¢¢
==
+++
2
ã1
311
1312323
, ãäå
()
R
U
III
RRRRRRR
.

48
I
ã
1
U
ã
2
+
R
2
R
3
I
2
I
3
a
)
R
3
á
)
R
2
I
3
¢
I
2
¢
R
3
â
)
R
2
I
3
¢¢
I
2
¢¢
R
ã
2
I
ã
1
R
ã
2
U
ã
2
+
R
ã
2
Ðèñ. 2.6
Òåïåðü ïîëàãàåì, ÷òî â öåïè äåéñòâóåò òîëüêî èñòî÷íèê U
ã2
. Èñ-
êëþ÷èâ èñòî÷íèê U
ã1
, ïîëó÷èì âòîðóþ ÷àñòè÷íóþ ñõåìó
(ðèñ. 2.5, â). Òîê I
3
²
îò âîçäåéñòâèÿ U
ã2
îïðåäåëèòñÿ êàê
¢¢¢¢¢¢
==
+++
1
ã2
322
1321313
, ãäå
()
R
U
III
RRRRRRR
.
Ðåçóëüòèðóþùèé òîê I
3
íàéäåì êàê àëãåáðàè÷åñêóþ ñóììó ÷àñ-
òè÷íûõ òîêîâ I
3
¢
è I
3
²
: I
3
= I
3
¢
+ I
3
²
. Ïðè îïðåäåëåíèè ðåçóëüòè-
ðóþùèõ òîêîâ çíàê «+» áåðóò ó ÷àñòè÷íûõ òîêîâ, ñîâïàäàþùèõ ñ
âûáðàííûì ïîëîæèòåëüíûì íàïðàâëåíèåì ðåçóëüòèðóþùåãî òîêà,
è çíàê «$» $ ó íåñîâïàäàþùèõ. Êàê ñëåäóåò èç ðàññìîòðåííîãî
ïðèìåðà, ïðè ñîñòàâëåíèè ÷àñòè÷íûõ ýëåêòðè÷åñêèõ ñõåì èñêëþ-
÷àåìûå èäåàëüíûå èñòî÷íèêè íàïðÿæåíèÿ çàêîðà÷èâàþòñÿ.  ñëó-
÷àå, åñëè â öåïè äåéñòâóþò èñòî÷íèêè íàïðÿæåíèÿ ñ âíóòðåííèìè
ñîïðîòèâëåíèÿìè R
ã
, ïðè èõ èñêëþ÷åíèè îíè çàìåíÿþòñÿ ñâîèìè
âíóòðåííèìè ñîïðîòèâëåíèÿìè R
ã
.
Ïðè íàëè÷èè èäåàëüíûõ èñòî÷íèêîâ òîêà ñîîòâåòñòâóþùèå âåò-
âè èñêëþ÷àåìûõ èñòî÷íèêîâ ðàçìûêàþòñÿ, à ïðè íàëè÷èè ðåàëü-
íûõ èñòî÷íèêîâ îíè çàìåíÿþòñÿ ñâîèìè âíóòðåííèìè ïðîâîäèìî-
ñòÿìè G
ã
.
Ïðèìåð. Îïðåäåëèòü òîê I
3
â öåïè, èçîáðàæåííîé íà ðèñ. 2.6, à. Ñîñòàâ-
ëÿåì äâå ÷àñòíûå ñõåìû (ðèñ. 2.6, á, â), äëÿ êîòîðûõ íàõîäèì ÷àñòè÷íûå òîêè:
2 ã2
ã2
3 ã13
2
ã23 ã223
;
RR
U
III
RRRRRR
+
¢¢
¢
==
++++
.
Ðåçóëüòèðóþùèé òîê I
3
= I
3
² $
I
3
¢
.
Ïðè íàëè÷èè â öåïè çàâèñèìûõ èñòî÷íèêîâ îíè îñòàþòñÿ â ÷àñ-
òè÷íûõ ñõåìàõ íåèçìåííûìè.
49
2.4. Ìåòîä êîíòóðíûõ òîêîâ
Ïðè îïðåäåëåíèè òîêîâ è íàïðÿæåíèé â îòäåëüíûõ âåòâÿõ öåïè
ñ n
â
-âåòâÿìè ïî çàêîíàì Êèðõãîôà â îáùåì ñëó÷àå íåîáõîäèìî ðå-
øèòü ñèñòåìó èç n
â
óðàâíåíèé. Äëÿ ñíèæåíèÿ ÷èñëà ðåøàåìûõ
óðàâíåíèé è óïðîùåíèÿ ðàñ÷åòîâ èñïîëüçóþò ìåòîäû êîíòóðíûõ
òîêîâ è óçëîâûõ íàïðÿæåíèé.
Ìåòîä êîíòóðíûõ òîêîâ ïîçâîëÿåò ñíèçèòü ÷èñëî ðåøàåìûõ
óðàâíåíèé äî ÷èñëà íåçàâèñèìûõ êîíòóðîâ, îïðåäåëÿåìûõ ðàâåí-
ñòâîì (1.15). Â åãî îñíîâå ëåæèò ââåäåíèå â êàæäûé êîíòóð óñ-
ëîâíîãî êîíòóðíîãî òîêà I
k
, íàïðàâëåíèå êîòîðîãî îáû÷íî âûáè-
ðàþò ñîâïàäàþùèì ñ íàïðàâëåíèåì îáõîäà êîíòóðà. Ïðè ýòîì äëÿ
êîíòóðíîãî òîêà áóäóò ñïðàâåäëèâû ÇÒÊ è ÇÍÊ.  ÷àñòíîñòè, äëÿ
êàæäîãî èç âûäåëåííûõ êîíòóðîâ ìîæíî ñîñòàâèòü óðàâíåíèÿ ïî
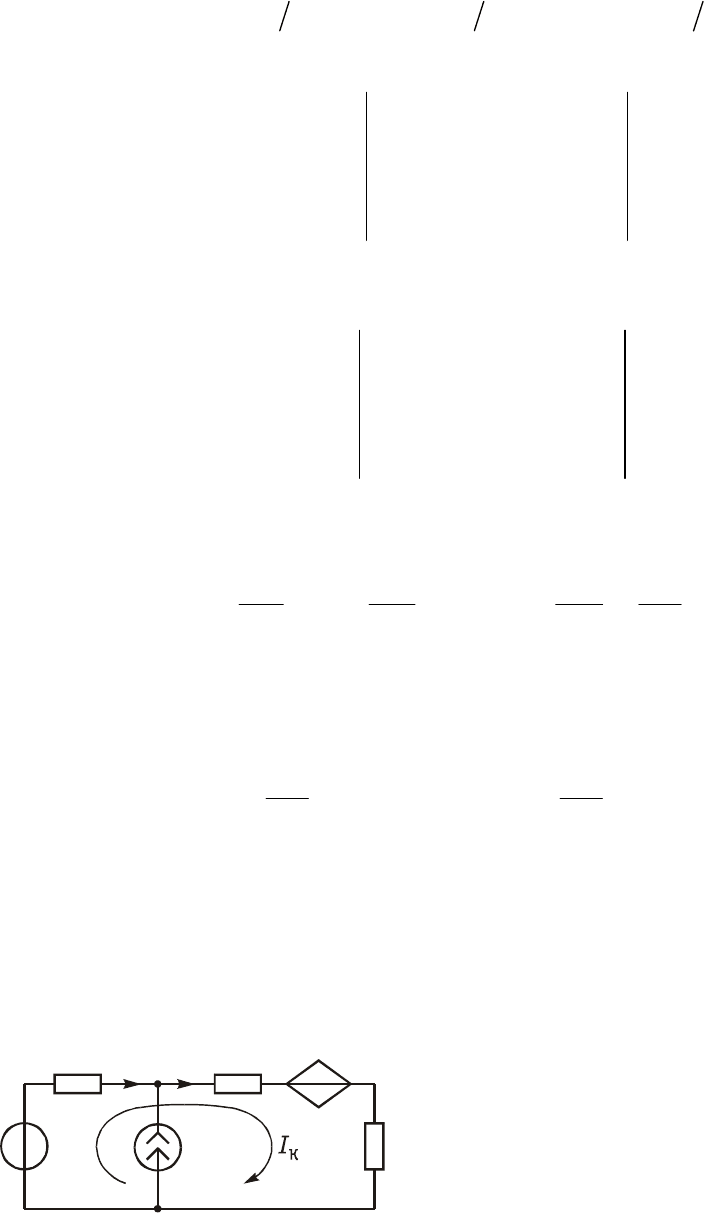
ÇÍÊ. Ïîÿñíèì ñóòü ìåòîäà êîíòóðíûõ òîêîâ íà ïðèìåðå ðåçèñòèâ-
íîé öåïè, ñõåìà êîòîðîé èçîáðàæåíà íà ðèñ. 2.5, à. Äëÿ êîíòóðíûõ
òîêîâ I
ê1
è I
ê2
ýòîé ñõåìû ìîæíî çàïèñàòü óðàâíåíèÿ ïî ÇÍÊ â âèäå
-+++=
ü
ý
-+++=
þ
ã113ê13ê2
ã23ê123ê2
()0,
()0.
URRIRI
URIRRI
Ïåðåíåñåì U
ã1
è U
ã2
â ïðàâóþ ÷àñòü ñèñòåìû è ïîëó÷èì òàê íà-
çûâàåìóþ êàíîíè÷åñêóþ ôîðìó çàïèñè óðàâíåíèé ïî ìåòîäó êîí-
òóðíûõ òîêîâ:
+=
ü
ý
+=
þ
11 ê112ê2ê1
21
ê122ê2ê2
,
,
RIRIU
RIRIU
ãäå R
11
= R
1
+ R
3
; R
22
= R
2
+ R
3
íàçûâàþò ñîáñòâåííûìè èëè
êîíòóðíûìè ñîïðîòèâëåíèÿìè I è II êîíòóðîâ: R
2
= R
21
= R
3
$
âçàèìíûìè ñîïðîòèâëåíèÿìè I è II êîíòóðîâ; U
ê1
= U
ã1
; U
ê2
=
= U
ã2
$ êîíòóðíûìè çàäàþùèìè íàïðÿæåíèÿìè. Èñòèííûå òîêè
â âåòâÿõ íàõîäÿòñÿ êàê àëãåáðàè÷åñêàÿ ñóììà êîíòóðíûõ òîêîâ:
I
1
= I
ê1
; I
2
= I
ê2
; I
3
= I
ê1
+ I
ê2
.
 îáùåì ñëó÷àå, åñëè ðåçèñòèâíàÿ öåïü ñîäåðæèò k íåçàâèñè-
ìûõ êîíòóðîâ, ñèñòåìà óðàâíåíèé èìååò âèä
+++=
ü
ï
+++=
ï
ý
ï
+++=
ï
þ
K
K
K
11 ê112ê2ê1
1 ê
21 ê122ê2ê2
2 ê
ê1ê2
12 êê
,
,
..................
.
kk
kk
kkkkkk
RIRIRIU
RIRIRIU
RIRIRIU
(2.11)
Ñëàãàåìûå R
ln
I
ên
â óðàâíåíèè (2.11) áåðóòñÿ ñî çíàêîì «+», åñëè
òîê I
êl
è I
ên
îáòåêàþò R
ln
â îäíîì íàïðàâëåíèè è ñî çíàêîì «$» â
ïðîòèâíîì ñëó÷àå. Êîíòóðíîå çàäàþùåå íàïðÿæåíèå U
ê
ðàâíî àë-
ãåáðàè÷åñêîé ñóììå çàäàþùèõ íàïðÿæåíèé èñòî÷íèêîâ, âõîäÿùèõ
â êàæäûé êîíòóð. Ñî çíàêîì «+» ñóììèðóþòñÿ èñòî÷íèêè, çàäàþ-
ùåå íàïðÿæåíèå êîòîðûõ íàïðàâëåíî íàâñòðå÷ó êîíòóðíîìó òîêó,
50
U
ã
1
+
R
2
I
2
R
3
R
1
I
1
U
ã
2
J
+
1
2
Ðèñ. 2.7
è ñî çíàêîì «$», åñëè íàïðàâëåíèå íàïðÿæåíèÿ è êîíòóðíîãî òîêà
ñîâïàäàþò.
Ðåøàÿ ñèñòåìó óðàâíåíèé (2.11), íàéäåì çíà÷åíèÿ êîíòóðíûõ
òîêîâ
=DD=DD=DD
K
ê11ê22
ê
;;
RRR
kk
III,
ãäå D
R
$ ãëàâíûé îïðåäåëèòåëü ñèñòåìû (2.11):
D=
K
K
K
1112
1
2122
2
12
..........
k
k
R
kkkk
RRR
RRR
RRR
. (2.12)
Îïðåäåëèòåëü D
k
íàõîäèòñÿ ïóòåì çàìåíû k-ãî ñòîëáöà â (2.12)
ïðàâîé ÷àñòüþ ñèñòåìû (2.11). Íàïðèìåð, äëÿ D
1
èìååì:
D=
K
K
K
ê112
1
ê122
2
1
ê2
..........
k
k
kkkk
URR
URR
URR
. (2.13)
Ðàçëàãàÿ îïðåäåëèòåëü D
1
ïî ýëåìåíòàì ïåðâîãî ñòîëáöà, ìîæåì
ïîëó÷èòü óðàâíåíèå äëÿ I
ê1
â äðóãîé ôîðìå:
=
D
DD
=+++=D
DDDD
å
K
1
1121
ê1ê1ê2
êê1
1
1
k
k
kll
l
RRRR
IUUUU, (2.14)
ãäå D
11
, D
12
, ..., D
k1
$ àëãåáðàè÷åñêèå äîïîëíåíèÿ îïðåäåëèòåëÿ
(2.12).
Àíàëîãè÷íûå óðàâíåíèÿ ìîæíî ïîëó÷èòü äëÿ îñòàëüíûõ òîêîâ:
==
=D=D
DD
åå
K
ê2
ê2êêê
11
11
,,
kk
llkll
ll
RR
IUIU. (2.15)
Êàê ñëåäóåò èç óðàâíåíèé (2.14) è (2.15), êîíòóðíûé òîê ìîæåò
áûòü ïîëó÷åí àëãåáðàè÷åñêèì ñóììèðîâàíèåì ÷àñòè÷íûõ òîêîâ îò
âîçäåéñòâèÿ êàæäîãî êîíòóðíîãî çàäàþùåãî íàïðÿæåíèÿ â îòäåëü-
íîñòè. Òàêèì îáðàçîì, ïîëó÷åííûé ðåçóëüòàò îòðàæàåò ðàñ-
ñìîòðåííûé â § 1.6 ïðèíöèï íàëîæåíèÿ.
Åñëè â ñõåìå êðîìå èñòî÷-
íèêîâ íàïðÿæåíèÿ ñîäåðæèòñÿ ï-
âåòâåé ñ èñòî÷íèêàìè òîêà, òî íå-
çàâèñèìûå êîíòóðû âûáèðàþòñÿ
òàê, ÷òîáû èñòî÷íèê òîêà âõîäèë
òîëüêî â îäèí êîíòóð. Ýòî ìîæíî
ñäåëàòü, åñëè âûáðàòü äåðåâî ãðà-
ôà öåïè òàêèì, ÷òîáû èñòî÷íèê
òîêà âõîäèë â îäíó èç õîðä.
