Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.

581
2. Íàéäèòå ñïåêòð äèñêðåòíîãî ñèãíàëà, ñîñòîÿùåãî èç îäíîãî îò-
ñ÷åòà x{ k} = {2}.
3. Êàêèì äîëæíî áûòü ñîîòíîøåíèå ìåæäó èíòåðâàëîì äèñêðåòè-
çàöèè ñïåêòðà ïî ÷àñòîòå DF è ïåðèîäîì ïîâòîðåíèÿ Ò
ñ
ñèãíàëà?
4. Íàéäèòå ÷àñòîòó äèñêðåòèçàöèè è èíòåðâàë äèñêðåòèçàöèè ñèã-
íàëà, èìåþùåãî ñïåêòð, îãðàíè÷åííûé ÷àñòîòîé F
â
= 10 êÃö.
5. Íàéòè äèñêðåòíóþ ñâåðòêó ñèãíàëîâ x
1
{ k } = {1; 1} è x
2
{k} = {0,5;
0,5; 0,5}.
Îòâåò: x
1
{k} * x
2
{k } = {0,5; 1; 1; 0,5}.
6. Âû÷èñëèòü ðåàêöèþ äèñêðåòíîé öåïè ñ èìïóëüñíîé õàðàêòåðè-
ñòèêîé h(k) íà âõîäíîé äèñêðåòíûé ñèãíàë x(k):
à) h{ k} = {2; 1; 0,5}, x{ k} = {0,5; 0,5}
á) h{ k} = {2; 2; 2}, x{k} = {1; 1; 1}.
Îòâåò: à) y{ k} = {1; 1,5; 0,75; 0,25}
á) y{ k} = {2; 4; 6; 4; 2}.
7. Íàéòè z-ïðåîáðàçîâàíèå äèñêðåòíûõ ñèãíàëîâ
à)
{
}
xk
= {3; 2; 1}
á)
{ }
{
1,
÷åòíîå
0,
íå÷åòíîå
k
xk
k
-
=
-
â)
{ }
( )
12,0
k
xkk=
.
Îòâåò: à)
( )
13
32
Xzzz
--
=++
á)
( )
(
)
2
11Xzz
-
=-
â)
( )
(
)
2
110,5Xzz
-
=- .
8. Íàéòè z-ïðåîáðàçîâàíèå äèñêðåòíîãî ñèãíàëà x
3
(k), ðàâíîãî
ñóììå ñèãíàëîâ x
1
{k} = {1; 0; 1; $1} è x
2
{k} = {2; 1; 0; 1}
Îòâåò:
( )
12
3
Xzzz
--
=++
.
9. Íàéòè äèñêðåòíûå ñèãíàëû x(k), èìåþùèå z-ïðåîáðàçîâàíèÿ
à)
( )
13
124
Xzzz
--
=++
á)
(
)
(
)
2
Xzzz
=-
.
Îòâåò: à) x{ k} = {1; 2; 0; 4}
á) x{ k}
2,0
n
n=
.
10. Íàéòè ÄÏÔ äèñêðåòíîãî ñèãíàëà x{k} = {0,5; 0,25; 0,0625}.
Ïîñòðîèòü ñïåêòð àìïëèòóä è ñïåêòð ôàç äèñêðåòíîãî ñèã-
íàëà.
Îòâåò: X{n} = {1,875; 0,838; 0,625; 0,838}
arg X{n} = {0; $0,464; 0,0464}.
11. Íàéòè îòñ÷åòû äèñêðåòíûõ ñèãíàëîâ x(k), èìåþùèõ ñïåêòðû
à) X{n} = {4; 0; 0; 0}
á) X{n} = {0; 4; 0; 0}.
582
y
()
k
+
+
T
T
y
()
k
+
T
T
xk
()
y
()
k
+
x
()
k
x
()
k
a
)
á
)
â
)
T
T
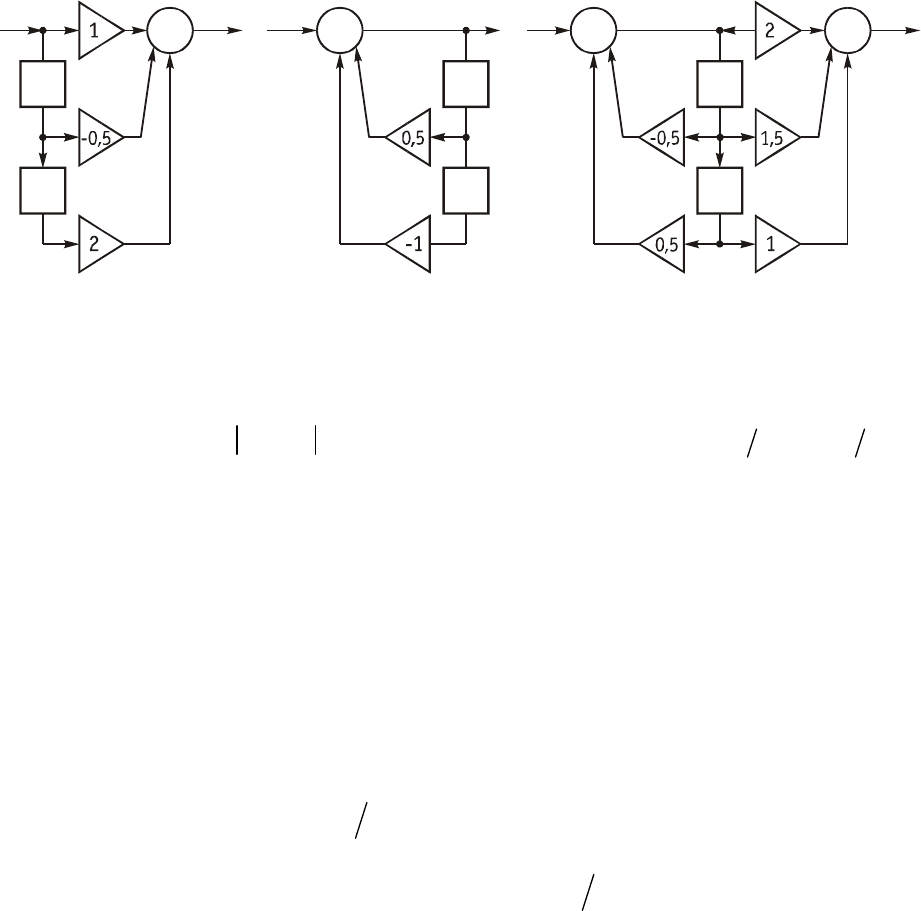
Ðèñ. 19.69
Îòâåò: à) x{ k} = {1; 1; 1; 1}
á)
{
}
xk
= {1; 1; 1; 1},
{
}
{
}
arg0;2;;2
xk
=pp-p
.
12. Çàïèñàòü ðàçíîñòíûå óðàâíåíèÿ äëÿ äèñêðåòíûõ öåïåé, ñòðóê-
òóðíûå ñõåìû êîòîðûõ ïðèâåäåíû íà ðèñ. 19.66.
Îòâåò: à)
(
)
(
)
(
)
(
)
0,5122
ykxkxkxk
=--+-
á)
(
)
(
)
(
)
(
)
0,512
ykxkykyk
=+---
â)
(
)
(
)
(
)
(
)
21,512
ykxkxkxk
=+-+--
(
)
(
)
0,510,52
ykyk
--+-
.
13. Çàïèñàòü ïåðåäàòî÷íûå ôóíêöèè öåïåé, ïðèâåäåííûõ íà
ðèñ. 19.66, è îïðåäåëèòü èõ èìïóëüñíûå õàðàêòåðèñòèêè.
Îòâåò: à)
( )
12
10,52
Hzzz
--
=-+, h{ k} = {1; $0,5; 2}
á)
( )
(
)
12
110,5Hzzz
--
=-+,
h{k} = {1; 0,5; $0,75; $0,875; ...}
â)
( )
(
)
(
)
1212
21,5210,50,5Hzzzzz
----
=+++- ,
h{k} = {2; 0,5; 1,75; $0,625; ...}.
14. Ðàññ÷èòàòü îòñ÷åòû y(0), y(1) è y(2) âûõîäíûõ ñèãíàëîâ öå-
ïåé, ïðèâåäåííûõ íà ðèñ. 19.66, åñëè âõîäíîé ñèãíàë $ ñòó-
ïåí÷àòàÿ ïîñëåäîâàòåëüíîñòü x{k } = u{ k} = {1; 1; 1; 1; ...}.
Îòâåò: à) y{ k} = {1; 0,5; 2,5}
á) y{ k} = {1; 1,5; 0,75}
â) y{ k} = {2; 2,5; 4,25}.
15. Îïðåäåëèòü èìïóëüñíûå õàðàêòåðèñòèêè öåïåé, îïèñûâàåìûõ
ðàçíîñòíûìè óðàâíåíèÿìè:
à)
(
)
(
)
(
)
(
)
0,5212
ykxkxkxk
=--+-
á)
(
)
(
)
(
)
(
)
3122
ykxkykyk
=--+-
â)
(
)
(
)
(
)
(
)
(
)
0,51212
ykxkxkykyk
=----+-
.
Îòâåò: à) h{ k} = {0,5; $2; 1}
á) h{ k} = {1; $3; 11; $39; ...}

583
â) h{ k} = {1; $2,5; 6; $14,5; ...}.
16. Îïðåäåëèòü ïåðåäàòî÷íûå ôóíêöèè öåïåé, îïèñûâàåìûõ ðàçíî-
ñòíûìè óðàâíåíèÿìè, ïðèâåäåííûìè â çàäà÷å 15.
Îòâåò: à)
( )
12
0,52
Hzzz
--
=-+
á)
( )
(
)
12
1132Hzzz
--
=+-
â)
( )
(
)
(
)
112
10,512Hzzzz
---
=-+-.
17. Ñîñòàâèòü ñòðóêòóðíûå ñõåìû, çàïèñàòü ðàçíîñòíûå óðàâíåíèÿ
è îïðåäåëèòü èìïóëüñíûå õàðàêòåðèñòèêè öåïåé, ïåðåäàòî÷íûå
ôóíêöèè êîòîðûõ èìåþò âèä
à)
( )
12
53
Hzzz
--
=-+
á)
( )
(
)
1
212Hzz
-
=-
â)
( )
(
)
(
)
11
21231Hzzz
--
=-++.
Îòâåò: à)
(
)
(
)
(
)
(
)
5132
ykxkxkxk
=--+-
,
{
}
hk
= {5; $1; 3}
á)
(
)
(
)
(
)
221
ykxkyk
=+-
,
()
22
k
hk
=×
= {2; 4; 8; 16; ...}
â)
(
)
(
)
(
)
(
)
(
)
541122
ykxkxkykyk
=--+-+-
,
{
}
hk
= {5; 1; 11; 13; ...}.
18. Îïðåäåëèòü óñòîé÷èâîñòü öåïåé, èìåþùèõ ïåðåäàòî÷íûå ôóíê-
öèè, ïðèâåäåííûå â çàäà÷å 17.
Îòâåò: à) óñòîé÷èâàÿ
á) íåóñòîé÷èâàÿ
â) íåóñòîé÷èâàÿ.
19. Îïðåäåëèòü ïåðåäàòî÷íóþ ôóíêöèþ öåïè, åñëè íà åå âõîäå è
âûõîäå äåéñòâóþò äèñêðåòíûå ñèãíàëû x{k} = {1; 0; 0; 0; 1; 0;
0; 0; 1; ...}, y{ k} = {1; 0; 1; 0; 1; 0; ...}.
Îòâåò:
( )
2
1
Hzz
-
=+
.
20. Íàéòè èìïóëüñíûå õàðàêòåðèñòèêè äèñêðåòíûõ öåïåé, èìåþ-
ùèõ ïåðåäàòî÷íûå ôóíêöèè
à)
( )
(
)
1
11
Hzz
-
=-
á)
(
)
(
)
(
)
11
112
Hzzz
--
=+-
Ñîñòàâèòü ñòðóêòóðíóþ ñõåìó êàñêàäíîãî ñîåäèíåíèÿ ýòèõ öå-
ïåé, îïðåäåëèòü äëÿ íåå ïåðåäàòî÷íóþ ôóíêöèþ è çàïèñàòü
ðàçíîñòíîå óðàâíåíèå.
Îòâåò: à)
(
)
hk
= 1, k
0
á)
( )
1,0
32,0
k
k
hk
k
=
ì
=
í
>
î
()
(
)
(
)
112
111,50,5Hzzzz
---
=+-+
(
)
(
)
(
)
(
)
(
)
11,510,52
ykxkxkykyk
=+-+---
.
584
21. Íàéòè ïåðåäàòî÷íóþ ôóíêöèþ äèñêðåòíîé öåïè ñ èìïóëüñíîé
õàðàêòåðèñòèêîé
à)
{
}
hk
= {1; $1}
á)
{ }
0,2,01
k
hkkN
=-
.
Îòâåò: à)
( )
1
1
Hzz
-
=-
á)
( )
(
)
1
110,2Hzz
-
=- .
22. Îïðåäåëèòü ñèãíàë íà âûõîäå äèñêðåòíîé öåïè ñ èìïóëüñíîé
õàðàêòåðèñòèêîé h{ k} = {1; 0,5}, åñëè íà âõîä ïîäàåòñÿ ñèãíàë
x{k} = {1; 1; 1}.
Îòâåò: y{ k} = {1; 1,5; 1,5; 0,5}.
23. Îïðåäåëèòü ïåðåäàòî÷íûå ôóíêöèè è À×Õ äèñêðåòíûõ öåïåé,
èìåþùèõ ðàçíîñòíûå óðàâíåíèÿ:
à)
(
)
(
)
(
)
0,51
ykxkxk
=--
á)
(
)
(
)
(
)
0,31
ykxkyk
=+-
.
Îòâåò: à)
( )
1
10,5
Hzz
-
=-
(
)
1,25cos2H
W=-pW
á)
( )
(
)
1
110,3Hzz
-
=-
(
)
11,090,6cos2H
W=-pW
.
24. Âû÷èñëèòü äèñïåðñèþ øóìà íà âûõîäå ÖÔ ïåðâîãî ïîðÿäêà ñ
ïåðåäàòî÷íîé ôóíêöèåé
(
)
(
)
1
1Hzabz
-
=-
; (b < 1) ñ èñïîëü-
çîâàíèåì ôîðìóëû (19.60).
Îòâåò:
2
2
2
1
121
b
x
D
s=×
-
.
585
ÏÐÅÄÌÅÒÍÛÉ ÓÊÀÇÀÒÅËÜ
Àâòîãåíåðàòîð 375
Àâòîêîëåáàíèÿ 375
Àêòèâíàÿ ñîñòàâëÿþùàÿ
$ ïðèëîæåííîãî íàïðÿæåíèÿ 80
$ òîêà 82
Àìïëèòóäà 73
$ òîêà êîìïëåêñíàÿ 77
Àïïðîêñèìàöèÿ
$ êóñî÷íî-ëèíåéíàÿ 252
$ ïîëèíîìèàëüíàÿ 246
Àòòåíþàòîðû 60
Áàëàíñ
$ àìïëèòóä 370, 379
$ ìîùíîñòè 39
$ ôàç 370, 379
Áåë 316
Áèåíèÿ 175
Âåòâü 25
Âêëþ÷åíèå
$ âñòðå÷íîå 90
$ ñîãëàñíîå 90
$ ñîãëàñîâàííîå 312
Âîëíû
$ áåãóùèå 345
$ îòðàæåííûå 335
$ ïàäàþùèå 335
$ ñìåøàííûå 350
$ ñòîÿ÷èå 347
Âîëüòìåòð ëèíåéíûé 353
Ãèðàòîð 107, 438
Ãîäîãðàô 112, 359
Ãðàô
$ öåïè 25
$ $ îðèåíòèðîâàííûé 25
Ãðóïïîâîå âðåìÿ ïðîõîæäåíèÿ 479
Äâóõïîëþñíèê
$ àêòèâíûé 35
$ ïàññèâíûé 35
Äâóõïîëþñíèêè
$ îáðàòíûå 135
$ ïàññèâíûå ðåàêòèâíûå 134
$ ïîòåíöèàëüíî îáðàòíûå 135
$ ýêâèâàëåíòíûå 135
Äåêðåìåíò
$ çàòóõàíèÿ 171
$ $ ëîãàðèôìè÷åñêèé 171
Äåðåâî ãðàôà 26
Äåöèáåë 316
Äèàãðàììà
$ âåêòîðíàÿ 76
$ ïîëþñíî-íóëåâàÿ 136
$ ñïèðàëüíàÿ 340
Äèñêðåòíîå ïðåîáðàçîâàíèå Ôóðüå
$ îáðàòíîå 523
$ ïðÿìîå 523
Äëèíà âîëíû 344
Äîáðîòíîñòü
$ êîíòóðà 114
$ ïîëþñà 421
Äîïîëíåíèå 26
Åìêîñòü 15
$ äèôôåðåíöèàëüíàÿ 237
$ ñòàòè÷åñêàÿ 237
Çàäà÷à
$ àíàëèçà 28
$ àïïðîêñèìàöèè 414
$ ðåàëèçàöèè 414
$ ñèíòåçà 28
$ $ ýëåêòðè÷åñêèõ öåïåé 412
Çàäà÷è ñ íóëåâûìè
$ íà÷àëüíûìè óñëîâèÿìè 159
Çàæèì îäíîèìåííûé 91
Çàæèìû
$ âõîäíûå 291
$ âûõîäíûå 291
Çàêîí
$ âòîðîé êîììóòàöèè 159
$ Ìàêñâåëëà%Ôàðàäåÿ 89
$ íàïðÿæåíèé Êèðõãîôà 29, 194, 222
$ Îìà â îïåðàòîðíîé ôîðìå 194
$ ïåðâûé êîììóòàöèè 158
$ òîêîâ Êèðõãîôà 28, 194
Çàòóõàíèå êîíòóðà 114
Çíà÷åíèå
$ äåéñòâóþùåå 74
$ íàïðÿæåíèÿ ìãíîâåííîå 11
$ ñðåäíåå 75
$ ñðåäíåêâàäðàòè÷åñêîå 74
$ òîêà ìãíîâåííîå 10
Èçáèðàòåëüíîñòü
$ ñâÿçàííûõ êîíòóðîâ 128
Èçîáðàæåíèå
$ ïî Ëàïëàñó 186, 528
Èçîõðîíèçì 174
Èíâåðòîð ñîïðîòèâëåíèÿ
$ ïîëîæèòåëüíûé 107
586
Èíäóêòèâíîñòü 14
$ âçàèìíàÿ 17, 89
$ äèôôåðåíöèàëüíàÿ 236
$ ñòàòè÷åñêàÿ 236
Èíòåãðàë
$ íàëîæåíèÿ 207
Èíòåðâàë
$ äèñêðåòèçàöèè 516
Èíòåðïîëÿöèÿ 246, 423
Èñêàæåíèå ñèãíàëà 476
Èñêàæåíèÿ
$ àìïëèòóäíî-÷àñòîòíûå 476
$ íåëèíåéíûå 268
$ ôàçî-÷àñòîòíûå 478
Èñòî÷íèê 12
$ çàâèñèìûé 19
$ íàïðÿæåíèÿ íåçàâèñèìûé 18
$ òîêà íåçàâèñèìûé 18
Êàòóøêà
$ âòîðè÷íàÿ 98
$ ïåðâè÷íàÿ 98
Êâàäðàò ìîäóëÿ
$ ïåðåäàòî÷íîé ôóíêöèè 417
Êâàçèïåðèîä 171
Êîäû äâîè÷íûå 568
Êîììóòàöèÿ 158
Êîìïîíåíòû ãèáðèäíûå 12
Êîíâåðòîð 64
Êîíòóð 26
$ êîëåáàòåëüíûé 113
$ $ ñâÿçàííûé 128
$ ïàðàëëåëüíûé 113
$ ïîñëåäîâàòåëüíûé 113
Êîððåêòîðû
$ àìïëèòóäíûå 453
$ ëèíåéíûõ èñêàæåíèé 413
$ ôàçîâûå 479
Êîýôôèöèåíò
$ àìïëèòóäû 150
$ áåãóùåé âîëíû 351
$ âçàèìíîé èíäóêöèè 382
$ ãàðìîíèê 150
$ çàòóõàíèÿ êîíòóðà 168
$ èñêàæåíèé 150
$ ìîùíîñòè 102, 150
$ íåëèíåéíîñòè 269
$ íåðàâíîìåðíîñòè îñëàáëåíèÿ 447
$ îñëàáëåíèÿ 339
$ îòðàæåíèÿ ïî íàïðÿæåíèþ 336
$ $ ïî òîêó 336
$ ðàñïðîñòðàíåíèÿ 332
$ ðàññåÿíèÿ 91
$ ñâÿçè 90
$ ñòîÿ÷åé âîëíû 351
$ òðàíñôîðìàöèè 101
$ ôàçû 339
$ ôîðìû 150
Êîýôôèöèåíòû À.È. Áåðãà 273
Êðóòèçíà
$ äèôôåðåíöèàëüíàÿ 236
$ ñðåäíÿÿ ÂÀÕ 383
Ëèíèè
$ äëèííûå 327
$ çàäåðæêè 413, 505
$ îäíîðîäíûå 328, 330
Ìàòðèöà
$ ðåäóöèðîâàííàÿ 27
$ ñå÷åíèé 27
$ ñòðóêòóðíàÿ 27
$ $ ðåäóöèðîâàííàÿ 56
Ìåòîä
$ âûðàâíèâàíèÿ êîýôôèöèåíòîâ 439
$ Ãàóññà 67
$ Äàðëèíãòîíà 458
$ êîìïëåêñíûõ àìïëèòóä 76
$ êîíòóðíûõ òîêîâ 49
$ ìàòðè÷íûõ ýêñïîíåíò 180
$ ìåäëåííî ìåíÿþùèõñÿ àìïëèòóä 405
$ ïåðåìåííûõ ñîñòîÿíèÿ 178
$ ðàçðÿæåííûõ ìàòðèö 68
$ Ðóíãå-Êóòòà 181
$ ñèìâîëè÷åñêèé 83
$ òîêîâ âåòâåé 42
$ óçëîâûõ ïîòåíöèàëîâ 53
Ìåòîäû
$ ìàòðè÷íî-òîïîëîãè÷åñêèå 25
$ îáðàùåíèÿ 67
$ $ ìàòðèöû óçëîâîé ïðîâîäèìîñòè 68
$ ðàçíîñòíûå 183
Ìèêðîñõåìà 24
Ìîäåëè äèñêðåòíûå 68
Ìîùíîñòü
$ àêòèâíàÿ 102
$ êîìïëåêñíàÿ 102
$ ìãíîâåííàÿ 11
$ ïîëíàÿ 102
$ ðåàêòèâíàÿ 102
Íàïðÿæåíèå
$ êîíòóðíîå çàäàþùåå 49
$ îïåðàòîðíîå 194
$ ðàñ÷åòíîå 194
$ ýëåêòðè÷åñêîå 11
Íåïåð 316
Îáðàòíàÿ ñâÿçü
587
$ âíåøíÿÿ 378
$ îòðèöàòåëüíàÿ 359, 360, 377
$ ïàðàëëåëüíàÿ ïî íàïðÿæåíèþ 357
$ $ $ òîêó 357
$ ïîëîæèòåëüíàÿ 359, 360, 377
$ ïîñëåäîâàòåëüíàÿ ïî íàïðÿæåíèþ 357
$ $ $ òîêó 357
Îãðàíè÷èòåëü 283
Îïåðàòîð åäèíè÷íîé çàäåðæêè 535
Îñëàáëåíèå
$ öåïè 112
$ ÷åòûðåõïîëþñíèêà ðàáî÷åå 320
$ $ õàðàêòåðèñòè÷åñêîå 316
Îòñ÷åòû íåïðåðûâíîãî ñèãíàëà 513
Îøèáêè
$ íàëîæåíèÿ 521
$ îêðóãëåíèÿ 579
Ïàäåíèå íàïðÿæåíèÿ 11
Ïàðàìåòðû
$ âòîðè÷íûå 115
$ êîðîòêîãî çàìûêàíèÿ 311
$ îáîáùåííûå 295
$ ïåðâè÷íûå 115, 328
$ ïðîâîäèìîñòåé 295
$ ñîïðîòèâëåíèé 295
$ õîëîñòîãî õîäà 311
$ ÷åòûðåõïîëþñíèêà 294
$ $ õàðàêòåðèñòè÷åñêèå 317
Ïàðàìåòðû-êîýôôèöèåíòû 296
Ïåðåäàòî÷íàÿ ôóíêöèÿ
$ êîìïëåêñíàÿ 322
$ ðàáî÷àÿ 323
$ ÷åòûðåõïîëþñíèêà 321
Ïåðåìåííûå ñîñòîÿíèÿ 178
Ïåðèîä 73
Ïëîòíîñòü ñïåêòðàëüíàÿ
$ àìïëèòóä ñèãíàëà 211
$ êîìïëåêñíàÿ 211
$ ýíåðãèè ñèãíàëà 217
Ïîäãðàô 26
$ ñâÿçíûé 26
Ïîëèíîìû
$ Áàòòåðâîðòà 447
$ Áåññåëÿ 507
$ Ãóðâèöà 368
Ïîëîñà
$ çàäåðæèâàíèÿ 413
$ íåïðîïóñêàíèÿ 443
$ ïðîïóñêàíèÿ 413, 443
$ $ àáñîëþòíàÿ 118
Ïîñëåäîâàòåëüíîñòü
$ äèñêðåòèçèðóþùàÿ 513
Ïîñòîÿííàÿ õàðàêòåðèñòè÷åñêàÿ
$ ïåðåäà÷è ëèíèè 341
$ $ ÷åòûðåõïîëþñíèêà 321
$ ôàçû ëèíèè 341
Ïîòîê ðàññåÿíèÿ 91
Ïðàâèëî Ëåíöà 89
Ïðåîáðàçîâàíèå
$ áèëèíåéíîå 563
$ Ëàïëàñà îáðàòíîå 185
$ $ ïðÿìîå 185
$ Ôóðüå áûñòðîå 526
$ $ äèñêðåòíîå 522
$ $ îáîáùåííîå 217
$ $ îáðàòíîå 210
$ $ îäíîñòîðîííåå 214
$ $ ïðÿìîå 210
$ ÷àñòîòû 287, 447
Ïðèáëèæåíèå
$ ñðåäíåêâàäðàòè÷åñêîå 425
$ ôóíêöèé ïî Òåéëîðó 424
$ $ ïî ×åáûøåâó 424
Ïðèåìíèê 12
Ïðèíöèï
$ âçàèìíîñòè 53
$ äóàëüíîñòè 37
$ ìîäåëèðîâàíèÿ 12
$ íåïðåðûâíîñòè 158
$ ýêâèâàëåíòíîñòè 30
Ïðîâîäèìîñòü 13
$ âçàèìíàÿ 54
$ êîìïëåêñíàÿ 85
$ îïåðàòîðíàÿ 194
$ ïåðåäàòî÷íàÿ êîìïëåêñíàÿ 110
$ ïîëíàÿ 82
$ ðåàêòèâíàÿ 82
$ ñîáñòâåííàÿ 54
Ïóòü ïðîñòîé 25
Ïó÷íîñòü íàïðÿæåíèÿ 346
Ðàâåíñòâî
$ Ïàðñåâàëÿ 149, 217, 579
Ðàäèàí 317
Ðàññòðîéêà
$ àáñîëþòíàÿ 118
$ îáîáùåííàÿ 118
$ îòíîñèòåëüíàÿ 118
Ðåàêöèÿ ëèíåéíîé öåïè 33
Ðåàëèçàöèÿ êàñêàäíàÿ 440
Ðåáðî ãðàôà 26
Ðåæèì
$ áåãóùåé âîëíû 345
$ ðàáîòû îñíîâíîé 42
$ ñàìîâîçáóæäåíèÿ æåñòêèé 387
588
$ $ ìÿãêèé 386
$ ñìåøàííûõ âîëí 350
$ ñîãëàñîâàííîãî âêëþ÷åíèÿ
$ $ $ ÷åòûðåõïîëþñíèêà 313
$ ñòàòè÷åñêèé 41
$ ñòàöèîíàðíûé 377
$ $ óñòîé÷èâûé 385
$ ñòîÿ÷èõ âîëí 348, 349
Ðåçîíàíñ 113
$ áåçðàçëè÷íûé 124
$ âòîðîé ÷àñòíûé 131
$ íàïðÿæåíèé 113
$ ïåðâûé ÷àñòíûé 130
$ ïîëíûé 131
$ ñëîæíûé 131
$ òîêîâ 113
Ñàìîâîçáóæäåíèå 360, 376, 377
Ñâåðòêà
$ äèñêðåòíàÿ 539
$ ôóíêöèé 188
Ñâîéñòâî
$ êîììóòàòèâíîñòè 187
$ ëèíåéíîñòè 524
$ ôèëüòðóþùåå 189
Ñâÿçü
$ æåñòêàÿ 91
$ êðèòè÷åñêàÿ 132
$ îáðàòíàÿ 356
$ ñèëüíàÿ 132
$ ñëàáàÿ 132
Ñäâèã äèñêðåòíîãî ñèãíàëà 524
Ñå÷åíèå
$ ãëàâíîå 26
$ ãðàôà 26
Ñæàòèå ñèãíàëà 215
Ñèãíàë 12
$ íåïåðèîäè÷åñêèé 211
Ñèãíàëû
$ àíàëîãîâûå 512
$ äèñêðåòíûå 512
$ óçêîïîëîñíûå 275
$ öèôðîâûå 512
Ñèëà ýëåêòðîäâèæóùàÿ 18
Ñèíòåç ARC-öåïåé ïî ìîäåëÿì 439
Ñêâàæíîñòü èìïóëüñîâ 150
Ñêèí-ýôôåêò 17
Ñêîðîñòü
$ ðàñïðîñòðàíåíèÿ ôàçîâàÿ 335
Ñîåäèíåíèå
$ êàñêàäíîå 302
$ ïàðàëëåëüíîå 25, 303
$ ïàðàëëåëüíî-ïîñëåäîâàòåëüíîå 303
$ ïîñëåäîâàòåëüíîå 302
$ ïîñëåäîâàòåëüíî-ïàðàëëåëüíîå 303
Ñîîòíîøåíèÿ ïðåäåëüíûå 188
Ñîïðîòèâëåíèå 13
$ äèôôåðåíöèàëüíîå 235
$ åìêîñòíîå 79
$ èíäóêòèâíîå 79
$ êîìïëåêñíîå 84
$ êîíòóðà êðèòè÷åñêîå 172
$ êîíòóðíîå 49
$ ëèíèè âîëíîâîå 333, 337, 338
$ ïåðåäàòî÷íîå êîìïëåêñíîå 110
$ ïîëíîå 81
$ ðåàêòèâíîå 81
$ ðåçèñòèâíîå 13
$ ðåçîíàíñíîå ýêâèâàëåíòíîå 122
$ ñîáñòâåííîå 49
$ ñòàòè÷åñêîå 235
$ õàðàêòåðèñòè÷åñêîå 114, 312
$ öåïè îïåðàòîðíîå 194
Ñîñòàâëÿþùàÿ
$ íàïðÿæåíèÿ ðåàêòèâíàÿ 80
$ òîêà ðåàêòèâíàÿ 82
Ñïåêòð
$ äèñêðåòíîãî ñèãíàëà 518
$ ëèíåé÷àòûé ôàçîâûé 146
$ ñèãíàëà àìïëèòóäíûé 211
$ $ îáîáùåííûé 214
$ $ ôàçîâûé 211
Ñòàáèëèçàòîð
$ ïîñòîÿííîãî íàïðÿæåíèÿ 258
Ñõåìà
$ âòîðàÿ Êàóýðà137
$ $ Ôîñòåðà 137
$ åìêîñòíîé òðåõòî÷êè 395
$ èíäóêòèâíîé òðåõòî÷êè 391
$ êàíîíè÷åñêàÿ 548
$ Êàóýðà 137
$ ïåðâàÿ Êàóýðà 137
$ $ Ôîñòåðà 137
$ Ôîñòåðà 137
Ñõåìû
$ çàìåùåíèÿ ýêâèâàëåíòíûå 21
$ íåðåêóðñèâíûå 545
$ ðåêóðñèâíûå 545
$ ýêâèâàëåíòíûå îïåðàòîðíûå 195
Òàíãåíñ óãëà
$ äèýëåêòðè÷åñêèõ ïîòåðü 330
Òàíãåíñ-ôóíêöèÿ 417
Òåîðåìà
$ çàäåðæêè 534
$ çàìåùåíèÿ 34
589
$ çàïàçäûâàíèÿ 187
$ Êîòåëüíèêîâà 516
$ $ îáðàòíàÿ 523
$ ëèíåéíîñòè 215
$ $ (ñóïåðïîçèöèè) 531
$ îáðàòèìîñòè 53
$ îïåðåæàþùåãî ñäâèãà 534
$ îòñ÷åòîâ 517
$ ïîäîáèÿ 187
$ Ðýëåÿ 217
$ ñâåðòêè 215, 524, 535
$ ñìåùåíèÿ 187
$ Òåëëåäæåíà 38
$ óìíîæåíèÿ 535
Òîê ýëåêòðè÷åñêèé 10
Òîêè çàäàþùèå óçëîâûå 54
Òðàíñôîðìàòîð 98
$ èäåàëüíûé 101
$ ñîâåðøåííûé 101
Òðåóãîëüíèê
$ íàïðÿæåíèé 81
$ ñîïðîòèâëåíèé 81
$ ñ ôåððîìàãíèòíûì ñåðäå÷íèêîì 101
Òðåóãîëüíèêè
$ ìîùíîñòåé 103
$ òîêîâ è ïðîâîäèìîñòåé 82
Óãîë
$ îòñå÷êè 272
$ ïîòåðü 101
Óçåë
$ áàçèñíûé 27
$ èíòåðïîëÿöèè 246
$ ïðîñòîé 25
Óçëû íàïðÿæåíèÿ (òîêà) 346
Óðàâíåíèå
$ Âàí-äåð-Ïîëÿ 407
$ ðåàêöèè öåïè 179
$ ñîñòîÿíèÿ öåïè 178
Óðàâíåíèÿ
$ êîìïîíåíòíûå 65
$ ïåðåäà÷è äëèííîé ëèíèè 332
$ $ ÷åòûðåõïîëþñíèêà 294
$ ðàçíîñòíûå 545
$ òåëåãðàôíûå 331
$ òîïîëîãè÷åñêèå 65
Óðîâíè êâàíòîâàíèÿ 512
Óñèëåíèå
$ ëîãàðèôìè÷åñêîå 112
$ ïåòëåâîå 358
Óñëîâèå
$ áåçûñêàæåííîé ïåðåäà÷è 226
$ ñàìîâîçáóæäåíèÿ
LC-àâòîãåíåðàòîðà 382
Óñëîâèÿ
$ çàäà÷è íà÷àëüíûå 159
$ $ çàâèñèìûå 159
$ $ íåçàâèñèìûå 159
$ Ôèàëêîâà%Ãåðñòà 415
$ ôèçè÷åñêîé ðåàëèçóåìîñòè 415, 426
Ôàçà
$ òåêóùàÿ 73
$ õàðàêòåðèñòè÷åñêàÿ 317
Ôàçîâàÿ ïîñòîÿííàÿ
$ ÷åòûðåõïîëþñíèêà 317
Ôàêòîð ñâÿçè 132
Ôèëüòð
$ Áàòòåðâîðòà 447
$ Çîëîòàðåâà 446
$ Í×-ïðîòîòèïà 447
$ òðàíñâåðñàëüíûé 544
$ ×åáûøåâà 451
Ôèëüòðû
$ Áàòòåðâîðòà è ×åáûøåâà 446
$ êâàðöåâûå 473
$ ìàãíèòîñòðèêöèîííûå 473
$ ïüåçîýëåêòðè÷åñêèå 472
$ ñ èçîýêñòðåìàëüíûìè
$ $ õàðàêòåðèñòèêàìè 457
$ ñî âñïëåñêàìè
$ $ ðàáî÷åãî îñëàáëåíèÿ 454
$ ýëåêòðè÷åñêèå 413
$ ýëåêòðîìåõàíè÷åñêèå 473
Ôîðìà êàíîíè÷åñêàÿ 49
Ôóíêöèè
$ âåùåñòâåííûå ïîëîæèòåëüíûå 419
$ ïåðåäàòî÷íûå îïåðàòîðíûå 196
$ öåïåé ïåðåäàòî÷íûå 545
Ôóíêöèÿ
$ Äèðàêà 189
$ ïåðåäàòî÷íàÿ êîìïëåêñíàÿ 110, 230
$ $ ïî íàïðÿæåíèþ 110
$ $ ïî òîêó êîìïëåêñíàÿ 110
$ öåïè âõîäíàÿ êîìïëåêñíàÿ 112
Õàðàêòåðèñòèêà
$ âåáåð-àìïåðíàÿ 14
$ âîëüò-àìïåðíàÿ 13
$ âîëüò-êóëîííàÿ 15
$ ãðóïïîâîãî âðåìåíè ïðîõîæäåíèÿ 478
$ èìïóëüñíàÿ áåñêîíå÷íàÿ 546
$ $ êîíå÷íàÿ 546
$ ëîãàðèôìè÷åñêàÿ
$ $ àìïëèòóäíî-÷àñòîòíàÿ 112
$ öåïè àìïëèòóäíî-÷àñòîòíàÿ 111
$ $ èìïóëüñíàÿ 200
590
$ $ ïåðåõîäíàÿ 200
$ $ ôàçî-÷àñòîòíàÿ 111
Õàðàêòåðèñòèêè
$ íàïðÿæåíèÿ ðåçîíàíñíûå 116
$ ñòàòè÷åñêèå 235
$ òîêà ðåçîíàíñíûå 116
Õàðàêòåðèñòè÷åñêàÿ ïîñòîÿííàÿ
$ ïåðåäà÷è ÷åòûðåõïîëþñíèêà 314
Õîðäû 26
Öåïè
$ àâòîêîëåáàòåëüíûå 375
$ äèôôåðåíöèðóþùèå 104
$ èíòåãðèðóþùèå 104
$ ñ ïàðàìåòðàìè
$ $ ðàñïðåäåëåííûìè 17, 327
$ $ ñîñðåäîòî÷åííûìè 17, 326
$ ýëåêòðè÷åñêèå íåëèíåéíûå 266
Öåïü
$ äèñêðåòíàÿ 539
$ íåóñòîé÷èâàÿ 367
$ ïàðàìåòðè÷åñêàÿ 160
$ ðåçîíàíñíàÿ 113
$ ñ ïîñòîÿííûìè ïàðàìåòðàìè 160
$ óñòîé÷èâàÿ 367, 368, 370, 373
$ ýëåêòðè÷åñêàÿ 12
Öèêëû
$ íèçêîãî óðîâíÿ ïðåäåëüíûå 580
×àñòîòà
$ äèñêðåòèçàöèè 516
$ êîëåáàíèé
$ $ ñîáñòâåííûõ çàòóõàþùèõ 170
$ êîìáèíàöèîííàÿ 286
$ íîðìèðîâàííàÿ 446
$ ðåçîíàíñíàÿ 113
$ öèêëè÷åñêàÿ 73
×åòûðåõïîëþñíèêè 291
$ àêòèâíûå 293
$ ëèíåéíûå 292
$ íåëèíåéíûå 292
$ íåîáðàòèìûå 294
$ íåñèììåòðè÷íûå 293
$ íåóðàâíîâåøåííûå 293
$ îáðàòèìûå 294
$ ïàññèâíûå 293
$ ñèììåòðè÷íûå 293
$ óðàâíîâåøåííûå 293
$ ýêâèâàëåíòíûå 296
×óâñòâèòåëüíîñòü
$ õàðàêòåðèñòèêè 421
Øóì êâàíòîâàíèÿ 578
Ýëåìåíò
$ åìêîñòíîé 15
$ èíäóêòèâíûé 14
Ýëåìåíòû
$ äâóõïîëþñíûå 17
$ ìíîãîïîëþñíûå 17
$ òðåõïîëþñíûå 17
$ ÷åòûðåõïîëþñíûå 17
Ýíåðãèÿ ýëåêòðè÷åñêàÿ 11
Z-ïðåîáðàçîâàíèå 528
