Бакалов В.П. Основы теории цепей. 3-е издание

Подождите немного. Документ загружается.

511

Òàáëèöà

f, êÃö 0 5 10 15 20 25 30 35 40 45 50

, äÁ 15,6

10,5

6,3 4,0 2,7 1,9 1,4 1,1 0,9 0,7 0,6

Îòâåò:

( )

RRCLC

HpH

RCLC

+a+w

=×=

+a+w

12. Êàêîâ ïîðÿäîê ðàñ÷åòà ïàññèâíîãî àìïëèòóäíîãî êîððåêòîðà?

13. Ðàññ÷èòàòü ýëåìåíòû, îáðàçóþùèå äâóõïîëþñíèê Z

àìïëèòóä-

íîãî êîððåêòîðà, ÷àñòîòíàÿ çàâèñèìîñòü îñëàáëåíèÿ A

(f) êîòî-

ðîãî ïðèâåäåíà â òàáëèöå, à çíà÷åíèå R

= 200 Îì.

Îòâåò: R

= 1 êÎì, C

= 51 íÔ.

14. Çà÷åì ïðèìåíÿþò êàñêàäíîå ñîåäèíåíèå òèïîâûõ çâåíüåâ êîð-

ðåêòîðîâ?

15. Ñôîðìóëèðîâàòü óñëîâèÿ áåçèñêàæåííîé ïåðåäà÷è ñèãíàëà.

16. Ïî÷åìó ïðîèñõîäÿò ôàçî-÷àñòîòíûå èñêàæåíèÿ?

17. ×òî òàêîå ãðóïïîâîå âðåìÿ ïðîõîæäåíèÿ?

18. Ïî ðèñ. 18.12 ïîÿñíèòü, êàê ðàáîòàåò ôàçîâûé êîððåêòîð.

19. Êàêèì îáðàçîì ñòðîÿòñÿ ïàññèâíûå ôàçîâûå êîððåêòîðû?

20. Êàê ðàññ÷èòûâàþòñÿ ïåðåäàòî÷íûå ôóíêöèè H

(p), ôàçîâûå

õàðàêòåðèñòèêè B

(w)è ÃÂÏ t

ãð

(w) ìîñòîâûõ ôàçîâûõ êîððåê-

òîðîâ 1-ãî è 2-ãî ïîðÿäêîâ?

21. Êàê èçìåíèòñÿ ãðàôèê t

ãð

(f) íà ðèñ. 18.32, á, åñëè èíäóêòèâ-

íîñòü L

óìåíüøèòü â 2 ðàçà.

22. Îïðåäåëèòü ïàðàìåòðû ýëåìåíòîâ ôàçîâîãî êîððåêòîðà 2-ãî ïî-

ðÿäêà (ðèñ. 18.32) ïî çàäàííûì êîýôôèöèåíòàì ïåðåäàòî÷íîé

ôóíêöèè w

4-1

0,41610c

=× , Q

= 0,25 è R

= 600 Îì.

Îòâåò: L

= 36 ìÃí; Ñ

= 1,6 ìêÔ;

= 0,58 Ãí; Ñ

= 0,1 ìêÔ.

23. Êàêèì îáðàçîì ñòðîÿòñÿ àêòèâíûå ôàçîâûå êîððåêòîðû?

24. Äîêàçàòü, ÷òî îïåðàòîðíàÿ ïåðåäàòî÷íàÿ ôóíêöèÿ H

(p) êîð-

ðåêòîðà, èçîáðàæåííîãî íà ðèñ. 18.35, èìååò âèä (18.30).

25. Êàêèì îáðàçîì íà îñíîâå ñõåìû ðèñ. 18.37 ïîëó÷èòü ôàçîâûå

êîððåêòîðû 1-ãî è 2-ãî ïîðÿäêîâ?

26. Êàê èçìåíèòñÿ ãðàôèê t

ãð

(f) íà ðèñ. 18.39, åñëè ñîïðîòèâëåíèå

: 1) óâåëè÷èòü â 4 ðàçà; 2) óâåëè÷èòü â 10 ðàç; 3) óìåíüøèòü

â 2 ðàçà?

27. Êàêîâ àëãîðèòì ðàñ÷åòà ôàçîâûõ êîððåêòîðîâ?

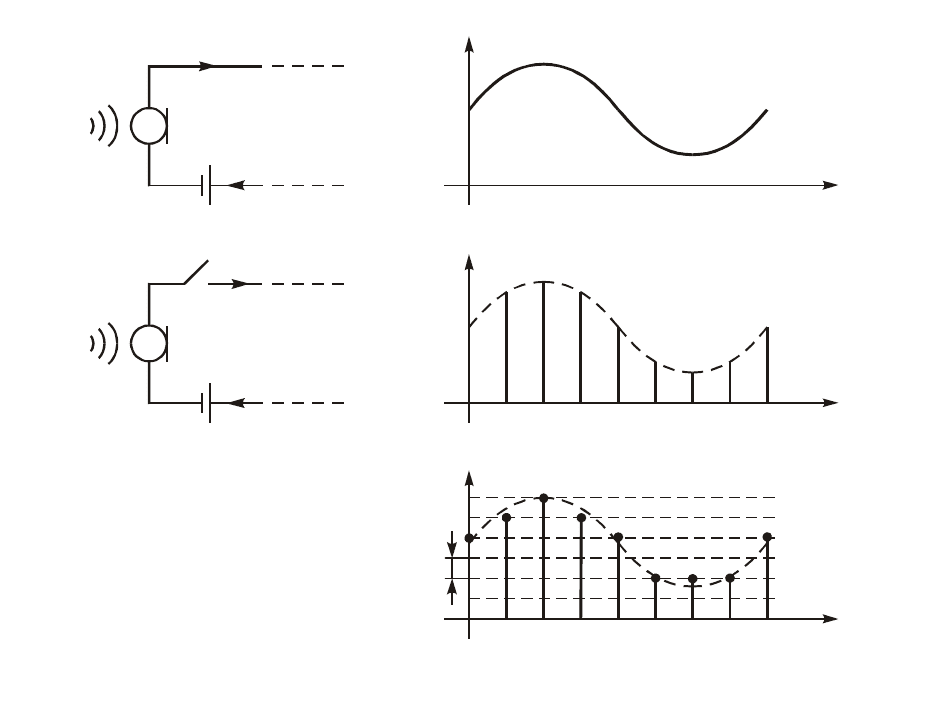
512

ÃËÀÂÀ 19. ÄÈÑÊÐÅÒÍÛÅ ÑÈÃÍÀËÛ È ÖÅÏÈ

19.1. Äèñêðåòíûå ñèãíàëû

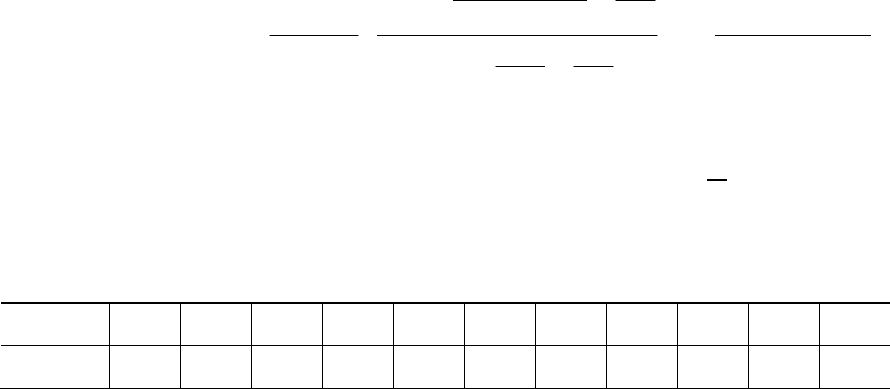
Äèñêðåòèçàöèÿ àíàëîãîâûõ ñèãíàëîâ. Ñèãíàë $ ýòî ôèçè÷åñêèé

ïðîöåññ (íàïðèìåð, èçìåíÿþùèåñÿ âî âðåìåíè òîêè è íàïðÿæå-

íèÿ), ñîäåðæàùèé â ñåáå íåêîòîðóþ èíôîðìàöèþ. Ëþáîé ñèãíàë

ìîæíî îïèñàòü ìàòåìàòè÷åñêîé ôóíêöèåé.

Ñóùåñòâóþò àíàëîãîâûå, äèñêðåòíûå è öèôðîâûå ñèãíàëû. Àíà-

ëîãîâûå ñèãíàëû îïèñûâàþòñÿ íåïðåðûâíîé âî âðåìåíè ôóíêöèåé

x(t), êîòîðàÿ ìîæåò ïðèíèìàòü ëþáûå çíà÷åíèÿ â îïðåäåëåííîì

èíòåðâàëå (íà ðèñ. 19.1 â êà÷åñòâå x(t) âçÿò òîê i(t) ìèêðîôîíà Ì);

äèñêðåòíûå ñèãíàëû x

(t) ïðåäñòàâëÿþò ñîáîé ïîñëåäîâàòåëüíîñòè

èëè îòñ÷åòû ôóíêöèè x(t), âçÿòûå â îïðåäåëåííûå äèñêðåòíûå ìî-

ìåíòû âðåìåíè kT (ðèñ. 19.1, á); öèôðîâûìè ÿâëÿþòñÿ ñèãíàëû,

êîòîðûå â äèñêðåòíûå ìîìåíòû âðåìåíè kT ïðèíèìàþò êîíå÷íûå

äèñêðåòíûå çíà÷åíèÿ $ óðîâíè êâàíòîâàíèÿ (ðèñ. 19.1, â), êîòî-

ðûå çàòåì êîäèðóþòñÿ öèôðîâûìè êîäàìè. (Íà ðèñ. 19.1, â, D $

øàã êâàíòîâàíèÿ).

Åñëè â öåïü ìèêðîôîíà (ðèñ. 19.1), ãäå òîê i(t) ÿâëÿåòñÿ íå-

ïðåðûâíîé ôóíêöèåé âðåìåíè, âñòðîèòü êëþ÷ è ïåðèîäè÷åñêè íà

êîðîòêèå ìãíîâåíèÿ çàìûêàòü åãî, òî òîê â öåïè áóäåò èìåòü âèä

óçêèõ èìïóëüñîâ ñ àìïëèòóäàìè, ïîâòîðÿþùèìè ôîðìó íåïðåðûâ-

()

Â ëèíèþ

Òîê â ëèíèè

. . .

)

()

. . .

)

Ðèñ.

513

íîãî ñèãíàëà. Ïîñëåäîâàòåëüíîñòü ýòèõ èìïóëüñîâ, êîòîðûå íàçû-

âàþò îòñ÷åòàìè íåïðåðûâíîãî ñèãíàëà, è ïðåäñòàâëÿåò ñîáîé, íå

÷òî èíîå, êàê äèñêðåòíûé ñèãíàë. Ïðè÷åì, âî âñåõ ýòèõ çàïèñÿõ

k $ öåëîå ÷èñëî, ïðèíèìàþùåå êàê ïîëîæèòåëüíûå, òàê è îòðèöà-

òåëüíûå çíà÷åíèÿ.

Â îòëè÷èå îò íåïðåðûâíîãî ñèãíàëà x(t) äèñêðåòíûé ñèãíàë

ìîæíî îáîçíà÷èòü x

(t). Òàê, íà ðèñ. 19.1 ïðè k < 0 äèñêðåòíûé

ñèãíàë i

(t) º 0. Ïðè k = 0 çíà÷åíèå i

(0T) ðàâíî çíà÷åíèþ ñèã-

íàëà i(t) â ìîìåíò âðåìåíè t = 0. Ïðè k > 0 îòñ÷åòû i(kT) ïîâòî-

ðÿþò ôîðìó ñèãíàëà i(t), ò.ê. èõ àìïëèòóäû ðàâíû çíà÷åíèÿì íå-

ïðåðûâíîãî ñèãíàëà â ìîìåíòû âðåìåíè kT.

Äèñêðåòíûå ñèãíàëû ìîæíî çàäàâàòü ãðàôèêàìè, êàê ýòî ïîêà-

çàíî íà ðèñ. 19.1, ôîðìóëàìè, íàïðèìåð,

(

)

(

)

sin2

itfkT

, â âè-

äå òàáëèö äèñêðåòíûõ çíà÷åíèé èëè äðóãèìè ñïîñîáàìè.

Öèôðîâûå ñèãíàëû è ôèëüòðû áóäóò ðàññìîòðåíû â § 19.8.

Ïðè ðàññìîòðåíèè äèñêðåòíûõ ñèãíàëîâ ÷àñòî âðåìÿ t íîðìè-

ðóþò ê ïåðèîäó äèñêðåòèçàöèè:

Ïðè ýòîì äèñêðåòíûé ñèãíàë ðàññìàòðèâàåòñÿ êàê ôóíêöèÿ öåëî-

÷èñëåííîé ïåðåìåííîé k:

(

)

(

)

xkTxk

Ìàòåìàòè÷åñêàÿ ìîäåëü äèñêðåòíîãî ñèãíàëà. Àíàëèòè÷åñêè

äèñêðåòíûé ñèãíàë õ

(t) óäîáíî ïðåäñòàâëÿòü ñ ïîìîùüþ äèñêðå-

òèçèðóþùåé ïîñëåäîâàòåëüíîñòè d-ôóíêöèé:

()

( )

fttkT

=-¥

=d-

(19.1)

Òîãäà õ

(t) ìîæíî ïðåäñòàâèòü â âèäå

() () () ()

( ) ( )( )

¥¥

=-¥=-¥

=×=d-=d-

åå

xtxtftxttkTxkTtkT

(19.2)

()

Ðèñ. 19.2 Ðèñ. 19.3

514

Ðèñ. 19.4

ò.å. äèñêðåòíûé ñèãíàë õ

(t) ñ ïîìîùüþ (19.2) ïðåäñòàâëÿåòñÿ â

âèäå ïîñëåäîâàòåëüíîñòè d-ôóíêöèé ñ âåñîâûìè êîýôôèöèåíòàìè,

ðàâíûìè îòñ÷åòàì õ(kT) àíàëîãîâîãî ñèãíàëà õ(t) â òî÷êàõ kT. Íà

ðèñ. 19.2 èçîáðàæåíà ñõåìà, èëëþñòðèðóþùàÿ ïðîöåäóðó ôîðìè-

ðîâàíèÿ äèñêðåòíîãî ñèãíàëà ñîãëàñíî ôîðìóëû (19.2).

Ðàññìîòðèì ïðèìåðû íåêîòîðûõ äèñêðåòíûõ ñèãíàëîâ, ïîëó÷åí-

íûõ èç òèïîâûõ àíàëîãîâûõ ñèãíàëîâ.

Ïðèìåð. Åäèíè÷íûé ñòóïåí÷àòûé àíàëîãîâûé ñèãíàë 1(t) ïðèâåäåí íà

ðèñ. 19.3.

Ñîîòâåòñòâóþùèé åìó äèñêðåòíûé ñèãíàë x

(t) íàçûâàåòñÿ ñòóïåí÷àòîé

ïîñëåäîâàòåëüíîñòüþ. Îí îïðåäåëÿåòñÿ ñëåäóþùèì îáðàçîì:

( )

{

1,0;

0,0.



Òàêàÿ ïîñëåäîâàòåëüíîñòü ïðèâåäåíà íà ðèñ. 19.3.

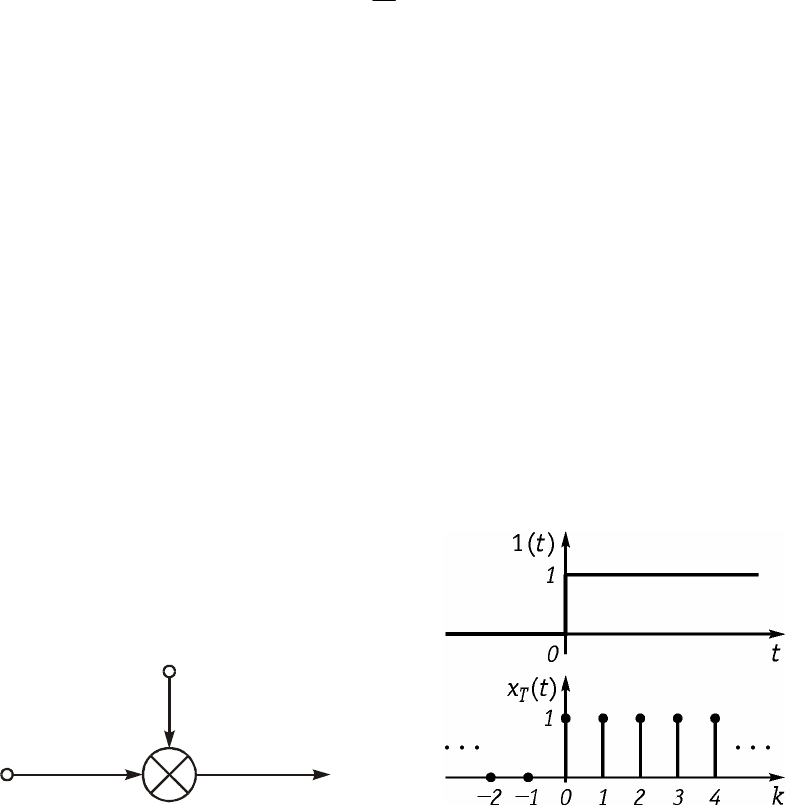
Ïðèìåð. Èìïóëüñ Äèðàêà èëè d-ôóíêöèÿ â àíàëîãîâîé îáëàñòè ïðèâåäåíà

íà ðèñ. 19.4, à.

Äåëüòà-ïîñëåäîâàòåëüíîñòü èëè äèñêðåòíàÿ d-ôóíêöèÿ îïðåäåëÿåòñÿ âûðà-

æåíèåì

( )

{

1,0;

0,0.

Ïîñëåäîâàòåëüíîñòü d

(t), ïðèâåäåííàÿ íà ðèñ. 19.4, á ïðèíèìàåò åäèíñò-

âåííîå çíà÷åíèå, ðàâíîå 1, ïðè k = 0. Ýòîò ñèãíàë ìîæíî ñäâèíóòü íà m èí-

òåðâàëîâ (ðèñ. 19.4, â ïðè m = 2):

( )

{

1,;

0,.

tmT

d-=

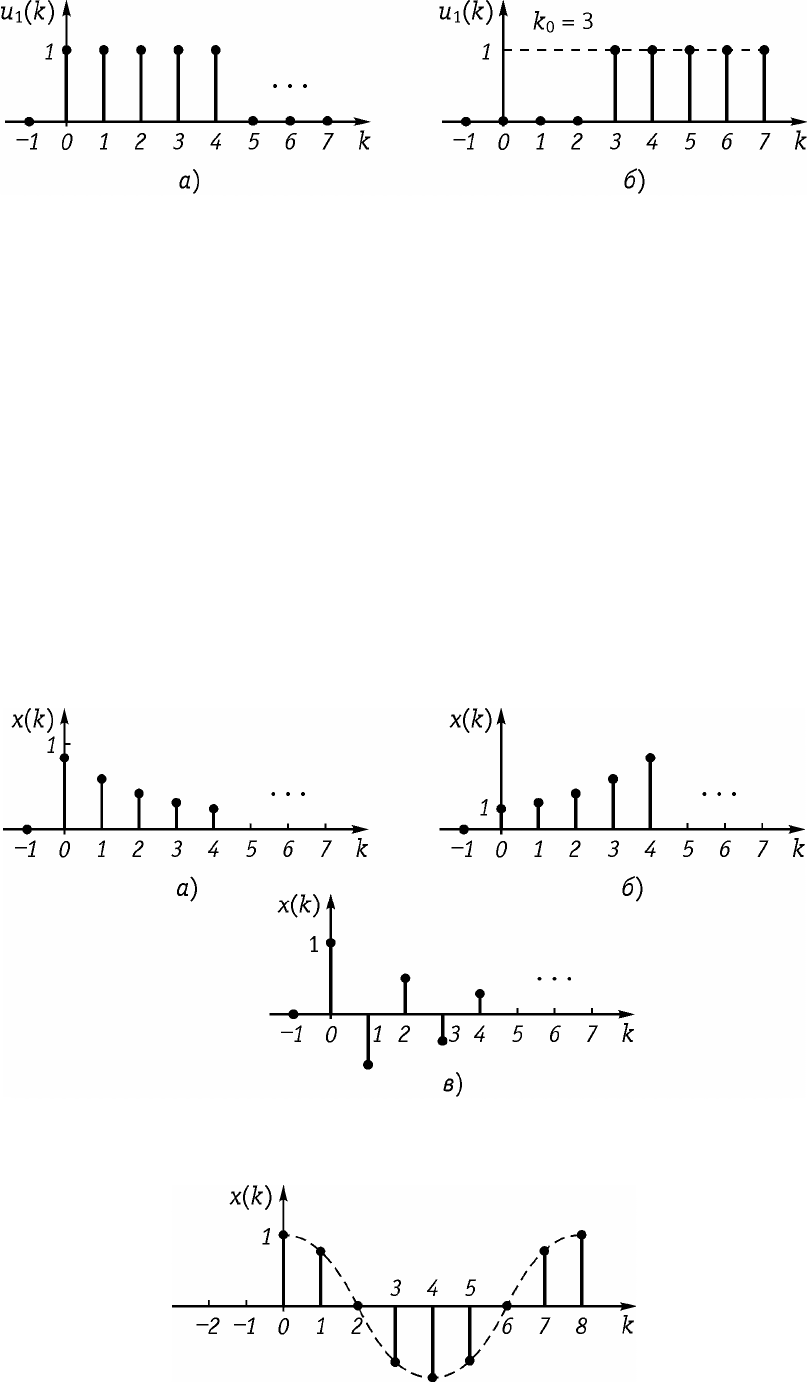
Ïðèìåð. Öèôðîâîé åäèíè÷íûé ñêà÷îê (ðèñ. 19.5, à), îïèñûâàåìûé îòíî-

øåíèåì

( )

{

1,0;

0,0,



èç êîòîðîãî ñëåäóåò, ÷òî äàííûé ñèãíàë ðàâåí åäèíèöå ïðè



è ðàâåí íó-

ëþ ïðè îñòàëüíûõ çíà÷åíèÿ k.

Çàäåðæàííûé öèôðîâîé åäèíè÷íûé ñêà÷îê (ðèñ. 19.5, á), îïèñûâàåìûé

ñîîòíîøåíèåì

515

Ðèñ. 19.5

( )

1,;

0,,

ukk



èç êîòîðîãî ñëåäóåò, ÷òî äàííûé ñèãíàë, â îòëè÷èå îò íåçàäåðæàííîãî, ðàâåí

åäèíèöå ïðè



è ðàâåí íóëþ ïðè îñòàëüíûõ çíà÷åíèÿ k.

Ïðèìåð. Äèñêðåòíàÿ ýêñïîíåíòà, îïèñûâàåìàÿ ñîîòíîøåíèåì

( )

,0;

0,0,



Åñëè |a| < 1, äèñêðåòíàÿ ýêñïîíåíòà íàçûâàåòñÿ óáûâàþùåé (ðèñ. 19.6, à),

à åñëè |a| > 1, $ âîçðàñòàþùåé (ðèñ. 19.6, á). Ïðè a < 0 ïîñëåäîâàòåëüíîñòü

áóäåò çíàêîïåðåìåííîé (ðèñ. 19.6, â), à ïðè à > 0 $ çíàêîïîñòîÿííîé. Ïðè

à = 1 âñå çíà÷åíèÿ îòñ÷åòîâ ïðè



îäèíàêîâû è ðàâíû åäèíèöå.

Ðèñ. 19.6

Ðèñ. 19.7

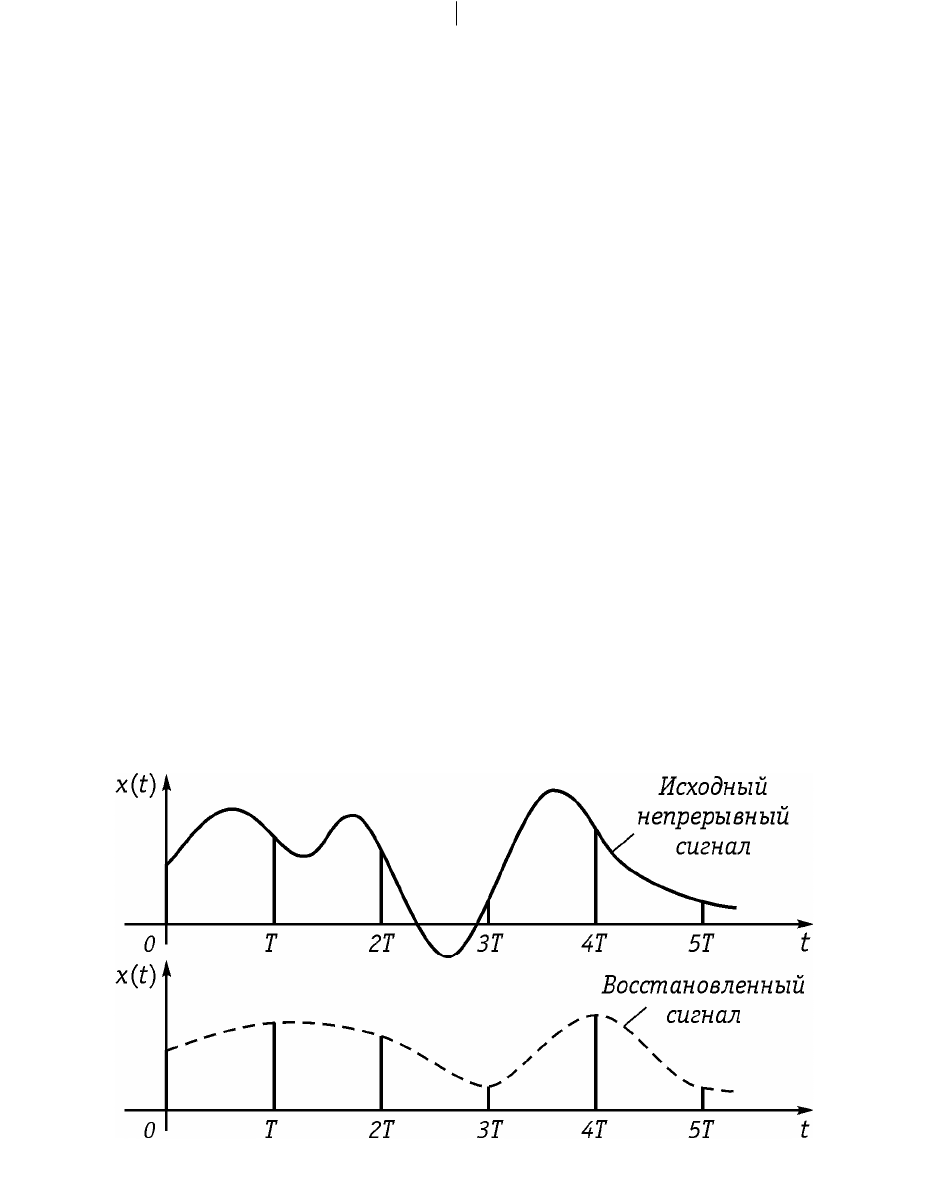
516

Ïðèìåð. Äèñêðåòíàÿ êîñèíóñîèäà (ñèíóñîèäà) (ðèñ. 19.7), îïèñûâàåìàÿ

ñîîòíîøåíèåì

(

)

(

)

(

)

=p=wcos2cos

xkAfTkATk

ãäå Ò $ ïåðèîä äèñêðåòèçàöèè; f, w $ ëèíåéíàÿ è öèêëè÷åñêàÿ ÷àñòîòû, ñâÿ-

çàííûå ñîîòíîøåíèå w = 2pf.

Äèñêðåòíàÿ êîñèíóñîèäà ñâÿçàíà ñ àíàëîãîâûì ãàðìîíè÷åñêèì ñèãíàëîì

ñëåäóþùèì îáðàçîì:

(

)

(

)

(

)

=w=wcoscos

tkT

xtAtATk

Ïðèìåð. Äèñêðåòíàÿ êîìïëåêñíàÿ ýêñïîíåíòà, îïèñûâàåìàÿ ñîîòíîøåíèåì

( )

jTk

xkAe ,

èëè, ñ ó÷åòîì ôîðìóëû Ýéëåðà

(

)

(

)

(

)

=w+wcossin

xkATkjATk

Èíòåðâàë âðåìåíè T, ÷åðåç êîòîðûé îòñ÷èòûâàþòñÿ çíà÷åíèÿ

íåïðåðûâíîãî ñèãíàëà õ(t), íàçûâàåòñÿ èíòåðâàëîì äèñêðåòèçà-

öèè. Îáðàòíàÿ âåëè÷èíà 1/T (îáîçíà÷èì åå f

) íàçûâàåòñÿ ÷àñòîòîé

âçÿòèÿ îòñ÷åòîâ èëè ÷àñòîòîé äèñêðåòèçàöèè.

Îòñ÷åòû íåïðåðûâíîãî ñèãíàëà ñëåäóåò áðàòü ñ òàêîé ÷àñòîòîé

(èëè ÷åðåç òàêîé èíòåðâàë âðåìåíè), ÷òîáû óñïåâàòü îòñëåäèòü âñå,

äàæå ñàìûå áûñòðûå, èçìåíåíèÿ ñèãíàëà. Èíà÷å, ïðè âîññòàíîâëå-

íèè ýòîãî ñèãíàëà ïî äèñêðåòíûì îòñ÷åòàì ÷àñòü èíôîðìàöèè áóäåò

ïîòåðÿíà è ôîðìà âîññòàíîâëåííîãî ñèãíàëà áóäåò îòëè÷àòüñÿ îò

ôîðìû èñõîäíîãî (ðèñ. 19.8). Åñëè îáðàòèòüñÿ ê ñõåìå ðèñ. 19.1,

òî ýòî îçíà÷àåò, ÷òî çâóê íà ïðèåìå áóäåò âîñïðèíèìàòüñÿ ñ èñêà-

æåíèÿìè.

Äëÿ ñèãíàëîâ ñ îãðàíè÷åííûì ñïåêòðîì, ò.å. ñèãíàëîâ, ó êîòî-

ðûõ ñïåêòð îãðàíè÷åí íåêîòîðîé âåðõíåé ÷àñòîòîé w

= 2pF

ñóùå-

ñòâóåò òåîðåìà Êîòåëüíèêîâà, îïðåäåëÿþùàÿ âûáîð èíòåðâàëà

Ðèñ. 19.8

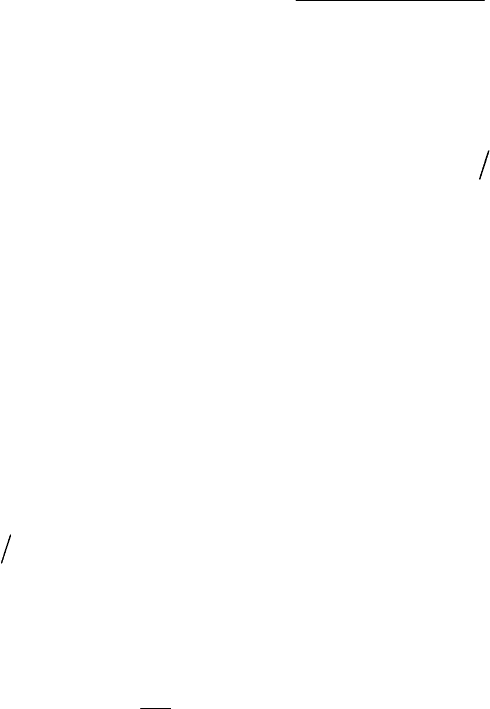
517

äèñêðåòèçàöèè T (èëè, ÷òî òî æå, ÷àñòîòû äèñêðåòèçàöèè f

). Ýòà

òåîðåìà âïåðâûå áûëà äîêàçàíà Â.À. Êîòåëüíèêîâûì â 1933 ã. â

ðàáîòå «Î ïðîïóñêíîé ñïîñîáíîñòè «ýôèðà» è ïðîâîëîêè â ýëåê-

òðîñâÿçè» ñòàâøåé îñíîâîïîëàãàþùåé â òåîðèè è òåõíèêå öèôðî-

âîé ñâÿçè.

Òåîðåìà Êîòåëüíèêîâà. Åñëè ôóíêöèÿ x(t) èìååò ñïåêòð, îã-

ðàíè÷åííûé âåðõíåé ÷àñòîòîé F

, òî x(t) ïîëíîñòüþ îïðåäåëÿ-

åòñÿ ïîñëåäîâàòåëüíîñòüþ ñâîèõ çíà÷åíèé (îòñ÷åòîâ) â ìîìåí-

òû âðåìåíè, îòñòîÿùèå äðóã îò äðóãà íà ïåðèîä Ò  1/2F

Ìàòåìàòè÷åñêè òåîðåìà Êîòåëüíèêîâà çàïèñûâàåòñÿ ñëåäóþùèì

îáðàçîì

()

( )

(

)

( )

sin

tkT

xtxkT

tkT

=-¥

(19.3)

ãäå w

= 2pF

; Ò = 1/2F

; x(kT) $ çíà÷åíèÿ (îòñ÷åòû) ôóíêöèè

x(t) â ìîìåíòû kT.

Äîêàçàòåëüñòâî òåîðåìû Êîòåëüíèêîâà äàåòñÿ â îáùåé òåîðèè ñâÿ-

çè. Çäåñü æå îòìåòèì, ÷òî ôóíêöèÿ âèäà

ââ

sin

¢¢

(t¢ = t $ kT)

èçâåñòíà íàì êàê ôóíêöèÿ îòñ÷åòîâ (ñì. § 5.3), ïîýòîìó òåîðåìó

Êîòåëüíèêîâà èíîãäà íàçûâàþò åùå òåîðåìîé îòñ÷åòîâ.

Ôèçè÷åñêèé ñìûñë òåîðåìû Êîòåëüíèêîâà (19.3) çàêëþ÷àåòñÿ â

òîì, ÷òî íåïðåðûâíàÿ ôóíêöèÿ x(t) ñ îãðàíè÷åííûì ñïåêòðîì F

ïîëíîñòüþ ìîæåò áûòü âîññòàíîâëåíà, åñëè èçâåñòíû åå îòñ÷åòû,

âçÿòûå ÷åðåç èíòåðâàë Ò  1/2F

. Ýòà òåîðåìà èãðàåò î÷åíü áîëü-

øóþ ðîëü â òåîðèè ñâÿçè, ò. ê. ïîçâîëÿåò ïåðåäà÷ó àíàëîãîâûõ

ñèãíàëîâ çàìåíèòü ïåðåäà÷åé äèñêðåòíûõ èëè öèôðîâûõ ñèãíà-

ëîâ, ÷òî ïîçâîëÿåò ñóùåñòâåííî ïîâûñèòü ýôôåêòèâíîñòü ñèñòåì

ñâÿçè.

Ó÷èòûâàÿ, ÷òî ñîãëàñíî òåîðåìû Êîòåëüíèêîâà ÷àñòîòà äèñêðå-

òèçàöèè

äâ

fTF

…

, ò.å. äîëæíà áûòü íå ìåíåå, ÷åì âäâîå ïðå-

âûøàòü âåðõíþþ ÷àñòîòó F

â ñïåêòðå àíàëîãîâîãî ñèãíàëà, òî ïðè

àíàëèçå äèñêðåòíûõ ñèãíàëîâ è öåïåé â ÷àñòîòíîé îáëàñòè ÷àñòî

ââîäÿò ïîíÿòèå íîðìèðîâàííîé ÷àñòîòû:

==w=w

èëè

ffTT

. (19.4)

19.2. Ñïåêòð äèñêðåòíîãî ñèãíàëà

Ïðåîáðàçîâàíèå Ôóðüå äëÿ äèñêðåòíîãî ñèãíàëà. Îïðåäåëèì

ñâÿçü ìåæäó ñïåêòðîì X(jw) àíàëîãîâîãî ñèãíàëà x(t) è ñïåêòðîì

(jw) äèñêðåòíîãî ñèãíàëà x

(t), îïðåäåëåííîãî ìîäåëüþ (19.2).

Ó÷èòûâàÿ, ÷òî x

(t) = x(t)f(t) ñîãëàñíî òåîðåìû ñâåðòêè (9.30)

ïîëó÷èì ñïåêòðàëüíóþ ïëîòíîñòü äèñêðåòíîãî ñèãíàëà

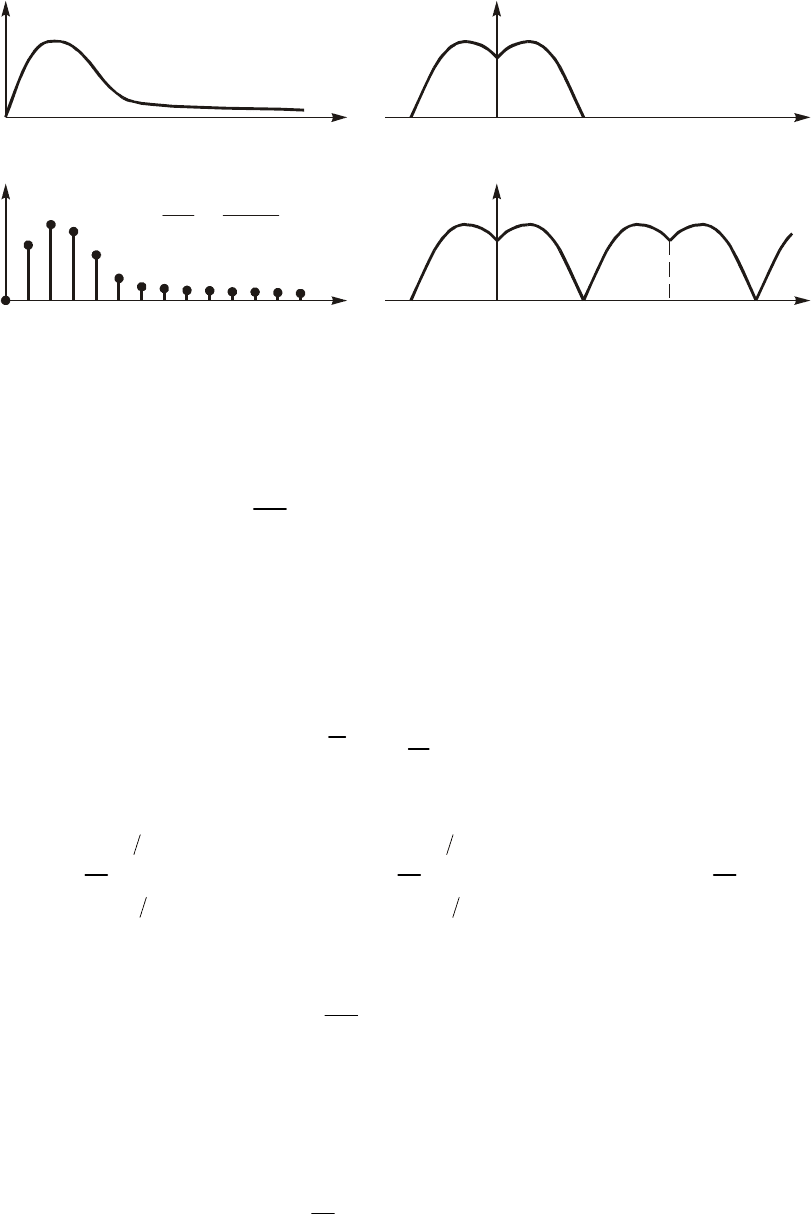
518

õt

()

() =

|Xj

()|

)

âä

()

Ðèñ. 19.9

( ) ( ) ( )

XjXjXjjd

-¥

w=Ww-WW

(19.5)

ãäå X

(jw) $ ñïåêòðàëüíàÿ ïëîòíîñòü äèñêðåòèçèðóþùåé ïîñëåäî-

âàòåëüíîñòè (19.1).

Äëÿ íàõîæäåíèÿ X

(jw) ðàçëîæèì f(t) â êîìïëåêñíûé ðÿä Ôó-

ðüå (5.6):

()

jkt

ftAe

=-¥

(19.6)

ãäå w

= 2p/Ò $ ÷àñòîòà äèñêðåòèçàöèè,

() ()

ää

222

jktjkt

Aftedttedt

TTT

-w-w

=×=d×=

òò

Îòñþäà ñîãëàñíî (9.42) ïîëó÷àåì

( )

Xjn

=-¥

w=dw-w

(19.7)

Ïîäñòàâèâ (19.7) â ôîðìóëó (19.5) ïîñëå èçìåíåíèÿ ïîðÿäêà

èíòåãðèðîâàíèÿ è ñóììèðîâàíèÿ è ñ ó÷åòîì ôèëüòðóþùåãî ñâîéñò-

âà d-ôóíêöèè îêîí÷àòåëüíî ïîëó÷èì

( )

XjXjjn

=-¥

w=w-w

(19.8)

Èç (19.8) ñëåäóåò âàæíûé âûâîä: ñïåêòð äèñêðåòíîãî ñèãíàëà

(t) (ðèñ. 19.9 á) ïðåäñòàâëÿåò ñîáîé ñóììó áåñêîíå÷íî áîëü-

øîãî ÷èñëà «êîïèé» ñïåêòðà àíàëîãîâîãî ñèãíàëà (ðèñ. 19.9, à),

ðàñïîëîæåííûõ íà îñè ÷àñòîò ÷åðåç îäèíàêîâûå èíòåðâàëû.

Ñëåäóåò îòìåòèòü, ÷òî ñîãëàñíî (19.8) è ðèñ. 19.9, á ýíåðãèÿ

ñïåêòðà äèñêðåòíîãî ñèãíàëà îêàçûâàåòñÿ áåñêîíå÷íî âåëèêà, ÷òî

519

ÿâëÿåòñÿ ñëåäñòâèåì èäåàëèçàöèè ðåàëüíîãî ñèãíàëà ìîäåëüþ

(19.2). Åñëè æå èñïîëüçîâàòü âìåñòî äèñêðåòèçèðóþùåé ïîñëåäîâà-

òåëüíîñòè (19.1) ïîñëåäîâàòåëüíîñòü èìïóëüñîâ êîíå÷íîé ýíåðãèè

(íàïðèìåð, ïðÿìîóãîëüíûõ èìïóëüñîâ), òî ïîëó÷èì ñïåêòð X

(jw),

ýíåðãèÿ êîòîðîãî óáûâàåò ñ ðîñòîì w («êîïèè» X(jw) ñ ðîñòîì w

óìåíüøàþòñÿ). Â òî æå âðåìÿ ñëåäóåò åùå ðàç ïîä÷åðêíóòü, ÷òî

ïðåäñòàâëåíèå äèñêðåòíîãî ñèãíàëà â ôîðìå (19.2) ñóùåñòâåííî

óïðîùàåò àíàëèç äèñêðåòíûõ ñèãíàëîâ è öåïåé è øèðîêî èñïîëüçó-

åòñÿ â ðàñ÷åòàõ.

Ñïåêòð äèñêðåòíîãî ñèãíàëà X

(jw) ìîæíî íàéòè è íåïîñðåäñò-

âåííî èç ïðÿìîãî ïðåîáðàçîâàíèÿ Ôóðüå (9.6) äëÿ äèñêðåòíîãî

ñèãíàëà (äåéñòâóåò â ìîìåíò t  0).

( )

()

( )( )

( ) ( )

jtjt

XjxtedtexkTtkTdt

xkTetkTdt

¥¥

-w-w

-w

w==d-=

=d-

òò

Îòñþäà ñ ó÷åòîì ôèëüòðóþùåãî ñâîéñòâà d-ôóíêöèè ïîëó÷èì

ïðÿìîå ïðåîáðàçîâàíèå Ôóðüå äëÿ äèñêðåòíûõ ñèãíàëîâ.

( )

jkT

XjxkTe

-w

(19.9)

è îáðàòíîå ïðåîáðàçîâàíèå Ôóðüå:

( )

0,5

jkT

xkTXjed

-w

=ww

(19.10)

Íà ïðàêòèêå â ôîðìóëàõ (19.9), (19.10) ÷àñòî âìåñòî çàâèñèìî-

ñòè X

(jw) ðàññìàòðèâàþò çàâèñèìîñòè X

(jf), êîòîðûå ëåãêî

ìîæíî ïîëó÷èòü ïóòåì çàìåíû w = 2pf.

Ïðèìåð. Ðàññ÷èòàåì ñïåêòð äèñêðåòíîãî ñèãíàëà, ñîñòîÿùåãî èç îäíîãî îò-

ñ÷åòà x

(t) = [a; 0; 0; 0; ...].

Âîñïîëüçóåìñÿ ôîðìóëîé (19.9), â êîòîðóþ ïîäñòàâèì çíà÷åíèÿ x

(t) çà-

äàííîãî ñèãíàëà

( )

220

jfkTjfT

XjfxkTeaea

-p-p××

===

Ïðèìåð. Ðàññ÷èòàåì ñïåêòð ýêñïîíåíöèàëüíîé äèñêðåòíîé ôóíêöèè x

(t) =

= 0,5

, k



Ãðàôèê äèñêðåòíîé ôóíêöèè x

(t) ïðèâåäåí íà ðèñ. 19.10, à åå îòñ÷åòû

ìîæíî çàïèñàòü â âèäå ïîñëåäîâàòåëüíîñòè x{k} = {1; 0,5; 0,25; 0,125;

0,0625; ...}.

Ñïåêòð äèñêðåòíîé ýêñïîíåíòû ðàññ÷èòàåì ïî ôîðìóëå (19.9)

520

. . .

234

()

0,1/

0,5/

()

Ðèñ. 19.10 Ðèñ. 19.11

( )

[ ]

0,5

jfkTkjfkT

XjfxkTee

¥¥

-p-p

=-¥=

===

åå

()

0,5,

10,5

jfT

-p

ãäå äëÿ ñóììèðîâàíèÿ ðÿäà èñïîëüçîâàíà ôîðìóëà

yyyy

=++++=

K .

Èñïîëüçóÿ ôîðìóëó Ýéëåðà

(cossin)

exjx

=+ , ïîëó÷èì âûðàæåíèå äëÿ

ðàñ÷åòà ñïåêòðà àìïëèòóä X(f).

( ) ( )

[ ]

( )

[ ]

=--p+-p

110,5cos20,5sin2XffTfT

Äëÿ ïîñòðîåíèÿ ãðàôèêà áóäåì çàäàâàòü çíà÷åíèÿ f îò 0 äî 1

Ò ñ øàãîì

0,1

T è ðàññ÷èòûâàòü X(f).

Ãðàôèê ñïåêòðà àìïëèòóä X(f) ýêñïîíåíöèàëüíîé äèñêðåòíîé ôóíêöèè

(t) = 0,5

ïðèâåäåí íà ðèñóíêå 19.11.

Êàê âèäíî èç ãðàôèêà, ñïåêòð äèñêðåòíîãî ñèãíàëà ñïëîøíîé è ïåðèîäè÷å-

ñêèé ñ ïåðèîäîì f

= 1

Ò.

Ñëåäóåò îòìåòèòü, ÷òî åñëè íå âûïîëíÿåòñÿ óñëîâèå òåîðåìû

Êîòåëüíèêîâà: f

 2f

, òî ñïåêòðû â (19.8) ÷àñòè÷íî ïåðåêðûâàþò-

ñÿ. Íà ðèñ. 19.12, ðèñ. 19.13 ïîêàçàí õàðàêòåð èçìåíåíèÿ ñïåêòðà

äèñêðåòíîãî ñèãíàëà X

(f) ïðè èçìåíåíèè ÷àñòîòû äèñêðåòèçàöèè

ñèãíàëà x

(t), îãðàíè÷åííîãî âî âðåìåíè èíòåðâàëîì T

(ðèñ.

19.12) è íåîãðàíè÷åííîãî âî âðåìåíè (ðèñ. 19.13).

Ðèñ. 19.12