Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.

531
Êàê óæå áûëî óñòàíîâëåíî, z-ïðåîáðàçîâàíèå ñèãíàëà x(k) = e
$
a
kT
èìååò
âèä
( )
T
z
Xz
ze
-a
=
-
.
Íóëü ôóíêöèè X(z) áóäåò â òî÷êå z
0
= 0, ïîëþñ $ â òî÷êå z
k
= e
$
a
T
. Ñëå-
äîâàòåëüíî, ðàäèóñ ñõîäèìîñòè r
0
= e
$
a
T
, à ôóíêöèÿ X(z) ñõîäèòñÿ ïðè
| z | > e
$
a
T
.
Îêðóæíîñòü, èìåþùàÿ ðàäèóñ ñõîäèìîñòè r
0
= e
$
a
T
, ïðèâåäåíà íà
ðèñ. 19.19. Îáëàñòü ñõîäèìîñòè íàõîäèòñÿ çà ïðåäåëàìè ýòîé îêðóæíîñòè.
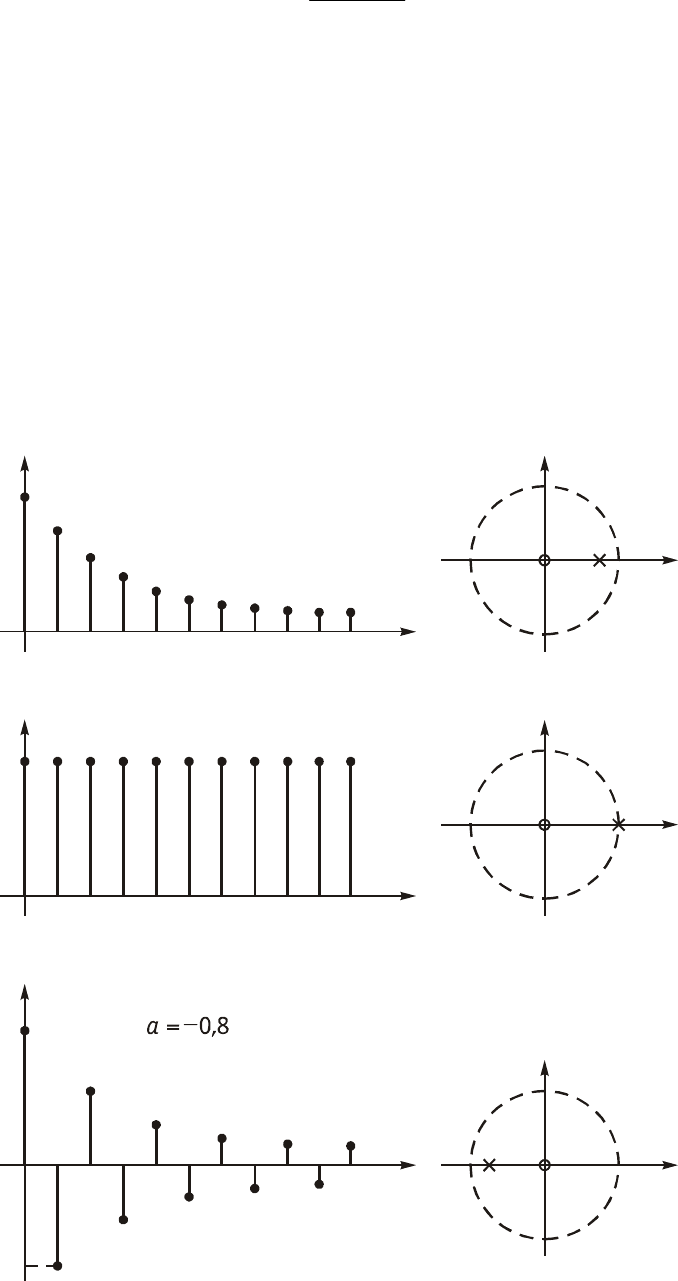
Ïðèìåð. Íàéäåì z-ïðåîáðàçîâàíèå ñèãíàëà x(k) = Aa
k
, k
0. Ýòîò äèñ-
êðåòíûé ñèãíàë ïîêàçàí íà ðèñ. 19.21 äëÿ òðåõ ðàçëè÷íûõ çíà÷åíèé a: à = 0,8;
à = 1; à = $0,8.
 ñîîòâåòñòâèè ñ (19.29) z-ïðåîáðàçîâàíèå òàêîãî äèñêðåòíîãî ñèãíàëà
ðàâíî
( )
¥
-
=
=
å
0
kk
k
XzAaz
. (19.33)
z
-ïëîñ-
êîñòü
z
-ïëîñ-
êîñòü
z
-ïëîñ-
êîñòü
0
0
0
1
1
1
2
2
2
3
3
3
4
4
4
5
5
5
6
6
6
7
7
7
8
8
8
9
9
9
10
10
10
k
k
k
. . .
. . .
a
= 0,8
z
0
= 0
z
0
= 0
z
0
= 0
z
k
= 0,8
z
k
= 0,8
_
z
k
= 1
0,8
_
A
a
= 1
xkAa
() =
k
xkAa
() =
k
xkAa
() =
k
A
A
A
j
1
j
1
j
1
_
j
1
_
j
1
_
j
1
1
1
1
0,8
_
0,8
_
1
_
1
_
1
a
)
á
)
â
)
Ðèñ. 19.21

532
Èç ìàòåìàòèêè èçâåñòíî, ÷òî ýòîò ðÿä ñõîäèòñÿ ê ôóíêöèè
( )
1
1
Az
XzA
za
az
-
==
-
-
, (19.34)
åñëè | az
$1
| < 1 èëè | z | > a.
Ôóíêöèÿ X(z) èìååò íóëü ïðè z = 0, à åå ïîëþñ z
n
= a ëåæèò íà îêðóæíî-
ñòè ðàäèóñîì R
0
= a, îãðàíè÷èâàþùåé îáëàñòü ñõîäèìîñòè.
Íà ðèñ. 19.21 ïîêàçàíî ðàñïîëîæåíèå íóëÿ è ïîëþñà ôóíêöèè X(z) â z-
ïëîñêîñòè ïðè ðàçëè÷íûõ à.
Íàõîæäåíèå äèñêðåòíîãî ñèãíàëà ïî åãî z-èçîáðàæåíèþ. Äëÿ
ýòîãî ìîæíî âîñïîëüçîâàòüñÿ îáðàòíûì z-ïðåîáðàçîâàíèåì (19.30).
Äðóãîé ñïîñîá çàêëþ÷àåòñÿ â òîì, ÷òîáû ðàçëîæèòü ôóíêöèþ
X(z) â ñòåïåííîé ðÿä ïî ñòåïåíÿì z
$1
. Òîãäà êîýôôèöèåíòû ïðè
ñòåïåíÿõ z
$1
áóäóò, â ñîîòâåòñòâèè ñ ôîðìóëîé (19.29), îòñ÷åòàìè
äèñêðåòíîãî ñèãíàëà x(k).
Ïðèìåð. Íàéäåì äèñêðåòíûé ñèãíàë x(k), êîòîðîìó ñîîòâåòñòâóåò z-ïðåîá-
ðàçîâàíèå X(z) = 1/(1 $ 0,5z
$1
).
Âîñïîëüçóåìñÿ ðàçëîæåíèåì ôóíêöèè (1 $ q)
$1
â ðÿä:
1 + q + q
2
+ q
3
+ ... .
Äëÿ çàäàííîãî z-ïðåîáðàçîâàíèÿ q = 0,5z
$1
, ïîýòîìó çàïèøåì z-ïðåîáðàçî-
âàíèå â âèäå
( )
---
=++++¼
123
10,50,250,125Xzzzz.
Ñðàâíèâàÿ ïîëó÷åííîå âûðàæåíèå ñ îáùåé ôîðìóëîé z-ïðåîáðàçîâàíèÿ
( )
( )
¥
-
=
=
å
0
k
k
Xzxkz
,
ïîëó÷èì ïîñëåäîâàòåëüíîñòü
x{k} = {1; 0,5; 0,25; 0,125; ...}.
Îáùèé ÷ëåí ýòîé ïîñëåäîâàòåëüíîñòè x(k) = 0,5
k
, k
0.
Ïðèìåð. Íàéäåì îòñ÷åòû äèñêðåòíîãî ñèãíàëà ïî åãî z-ïðåîáðàçîâàíèþ
( )
2
2
12
305
11
61
1
66
z
Xz
zz
zz
--
==
--
--
.
Äëÿ ðàçëîæåíèÿ ôóíêöèè X(z) â ñòåïåííîé ðÿä ïî ñòåïåíÿì z
$1
âûïîëíèì
äåëåíèå ÷èñëà 5 íà ìíîãî÷ëåí
12
11
1
66
zz
--
æö
--
ç÷
èø
.  ðåçóëüòàòå ïîëó÷èì ÷àñò-
íîå
12
535
5
636
zz
--
+++
K
. Îòñ÷åòû äèñêðåòíîãî ñèãíàëà ðàâíû
( )
() ()
===
535
05;1;2;
636
xxx è ò.ä.
Ïðîöåäóðà äåëåíèÿ çäåñü íå ïðèâåäåíà èç-çà åå ãðîìîçäêîñòè, õîòÿ âûðàæå-
íèÿ ïîëèíîìîâ, ñòîÿùèõ â ÷èñëèòåëå è çíàìåíàòåëå X(z), íå ñëèøêîì ñëîæíûå.
533
Áîëåå ýôôåêòèâíûì ñïîñîáîì íàõîæäåíèÿ x(k) ïî èçâåñòíîìó X(z) ÿâëÿ-
åòñÿ ñïîñîá ïîäîáíûé ìåòîäó ðàçëîæåíèÿ íà ïðîñòåéøèå äðîáè â ïðåîáðàçî-
âàíèÿõ Ëàïëàñà.
Ïðèìåð. Íàéäåì îáùèé ÷ëåí x
k
äèñêðåòíîãî ñèãíàëà x(k), êîòîðîìó ñîîò-
âåòñòâóåò z-èçîáðàæåíèå, çàäàííîå â ïðåäûäóùåì ïðèìåðå
( )
--
==
--
--
2
2
12
305
11
61
1
66
z
Xz
zz
zz
.
Ôóíêöèÿ X(z) èìååò ïîëþñû â òî÷êàõ z
1
= 1/2 è z
2
= $1/3, èëè, ÷òî òî
æå, â òî÷êàõ z
1
$1
= 2 è z
2
$1
= $3.
Ðàçëîæèì X(z) íà ñóììó ïðîñòûõ äðîáåé:
( )
--
--
==+
æöæö
-+
-+
ç÷
ç÷
èø
èø
11
11
532
11
11
11
11
23
23
Xz
zz
zz
. (19.35)
Êîýôôèöèåíòû â ÷èñëèòåëÿõ êàæäîé äðîáè âû÷èñëÿþòñÿ òàê æå, êàê ïðè ðàç-
ëîæåíèè âõîäíîãî ñîïðîòèâëåíèÿ z(p) ðåàêòèâíûõ äâóõïîëþñíèêîâ ïðè ñèí-
òåçå èõ ïî ñõåìå Ôîñòåðà:
1
11
1
2
1
51
2
3;
11
11
23
z
z
zz
-
--
-
=
æö
-
ç÷
èø
=
æöæö
-+
ç÷
ç÷
èø
èø
1
11
1
3
1
51
3
2.
11
11
23
z
z
zz
-
--
-
=-
æö
+
ç÷
èø
=
æöæö
-+
ç÷
ç÷
èø
èø
Ïîäîáíî òîìó, êàê ôîðìóëà (19.34) ïðåäñòàâëÿåò ñóììó ðÿäà (19.33), ïðî-
ñòûå äðîáè â (19.17) ÿâëÿþòñÿ ñóììàìè ðÿäîâ
0
1
3
2
k
k
k
z
¥
-
=
æö
ç÷
èø
å
è
0
1
2
3
k
k
k
z
¥
-
=
æö
-
ç÷
èø
å
.
Ïîñêîëüêó z-ïðåîáðàçîâàíèå $ ýòî ëèíåéíàÿ îïåðàöèÿ, òî ïîñëåäîâàòåëü-
íîñòü x(k) ñîñòîèò èç ñóììû äâóõ ïîñëåäîâàòåëüíîñòåé:
( )
11
32,0
23
kk
xkk
æöæö
=+-
ç÷ç÷
èøèø
.
Ïîñëå âûïîëíåíèÿ îïåðàöèè âîçâåäåíèÿ â ñòåïåíü k ïîëó÷èì îòñ÷åòû äèñ-
êðåòíîãî ñèãíàëà
( )
() ( )
535
05;1;2;
636
xxx===
è ò.ä.
Ñâîéñòâà z-ïðåîáðàçîâàíèÿ. Òàê æå êàê è äëÿ ïðåîáðàçîâàíèé
Ëàïëàñà è Ôóðüå, ñóùåñòâóþò òåîðåìû äëÿ z-ïðåîáðàçîâàíèÿ. Ïðè-
âåäåì íàèáîëåå âàæíûå òåîðåìû îäíîñòîðîííåãî z-ïðåîáðàçîâàíèÿ.
534
Òåîðåìà ëèíåéíîñòè (ñóïåðïîçèöèè). Ñóììå äèñêðåòíûõ ñèã-
íàëîâ ñîîòâåòñòâóåò ñóììà èõ z-èçîáðàæåíèé. Åñëè äèñêðåòíûì
ñèãíàëàì x(k) è y(k) ñîîòâåòñòâóþò z-èçîáðàæåíèÿ X(z) è Y(z), òî
(
)
(
)
(
)
(
)
axkbykaXzbYz
++
,
ãäå a è b $ íåêîòîðûå ÷èñëà.
Äîêàçàòåëüñòâî òåîðåìû âûïîëíèòå ñàìîñòîÿòåëüíî, èñïîëüçóÿ
âûðàæåíèå (19.29) äëÿ ðàñ÷åòà z-èçîáðàæåíèÿ äèñêðåòíîãî ñèãíàëà.
Òåîðåìà îïåðåæàþùåãî ñäâèãà. Åñëè äèñêðåòíîìó ñèãíàëó x(k)
ñîîòâåòñòâóåò îäíîñòîðîííåå z-ïðåîáðàçîâàíèå X(z), òî ñèãíàëó,
ñäâèíóòîìó íà îäèí èíòåðâàë äèñêðåòèçàöèè, x(k + 1) ñîîòâåòñò-
âóåò z-ïðåîáðàçîâàíèå z(X(z) $ x(0)).
Ìàòåìàòè÷åñêàÿ çàïèñü òåîðåìû èìååò âèä
(
)
(
)
(
)
(
)
1
0
xkz
Xzx
+
-
,
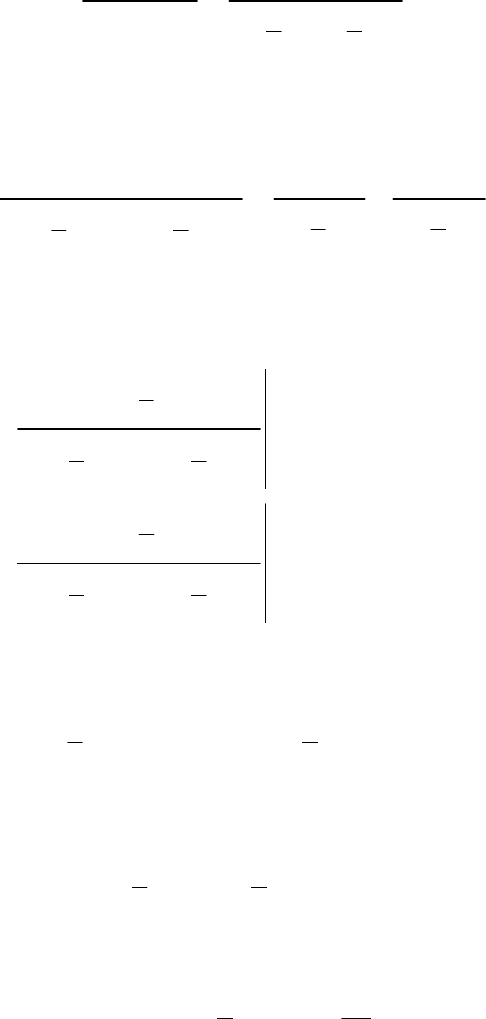
×òîáû äîêàçàòü òåîðåìó, âîñïîëüçóåìñÿ îñíîâíûì âûðàæåíèåì
(19.29) äëÿ ðàñ÷åòà z-ïðåîáðàçîâàíèÿ äèñêðåòíûõ ñèãíàëîâ x(k) è
x(k + 1), à òàêæå ãðàôèêàìè, ïðèâåäåííûìè íà ðèñ. 19.22.
( )
( )
( )
() ( )
12
0
012
k
k
Xzxkzxxzxz
¥
---
=
==+++
å
K
;
( )
( )
() ()
( )
12
0
1123
k
k
Xzxkzxxzxz
¥
---
=
¢
=+=+++
å
K
.
Ñðàâíèâàÿ X(z) è X
¢
(z), ïîëó÷àåì X
¢
(z) = z(X(z) $x(0)), ÷òî è
òðåáîâàëîñü äîêàçàòü.
Î÷åâèäíî, ÷òî òåîðåìà îïåðåæàþùåãî ñäâèãà âûïîëíÿåò òó æå
ñàìóþ ðîëü, ÷òî è òåîðåìà äèôôåðåíöèðîâàíèÿ äëÿ ïðåîáðàçîâà-
íèé Ëàïëàñà.
Òåîðåìà çàäåðæêè. Ìàòåìàòè÷åñêàÿ çàïèñü òåîðåìû èìååò âèä
( ) ( )
( )
,0
N
xkNukNzXzN
-
--×
.
 òåîðåìå çàäåðæêè u(k) $ ýòî äèñêðåòíûå îòñ÷åòû ôóíêöèè
åäèíè÷íîãî ñêà÷êà (ðèñ. 19.23)
( )
{
1,0,
0,0,
k
uk
k
=
<
0
0
1
1
2
2
3
3
4
4
5
_
1
k
k
xk
()
xk +
(1)
Ðèñ. 19.22

535
0
1
1
_
1
_
2
2
3
4
5
k
uk
()
()
1
1
1
-
-
=
z
z
X
0
1
1
_
1
_
2
N
_
1
N
+
1
N
k
uk N
()
_
()
1
N
1
-
-
-
=
z
z
z
X
~
~
Ðèñ. 19.23 Ðèñ. 19.24
à u(k $ N) $ ýòî äèñêðåòíûå îòñ÷åò ôóíêöèè u(k), çàäåðæàííîé
íà N èíòåðâàëîâ äèñêðåòèçàöèè (ðèñ. 19.24).
( )
{
0,,
1,.
kN
ukN
kN
<
-=
Äîêàçàòåëüñòâî âûòåêàåò èç îñíîâíîãî âûðàæåíèÿ (19.29) äëÿ z-
ïðåîáðàçîâàíèÿ.
( ) ( )
( )
()
( )
( )
( )
( )
() ( )
( )
( )
¥
---+-+
=
---
-
--=+++=
=+++=
=×
å
K
K
12
0
12
012
012
.
NNNN
k
N
N
xkNukNzxzxzxz
zxxzxz
zXz
Ïðè äîêàçàòåëüñòâå ó÷òåíî, ÷òî åäèíè÷íàÿ ñòóïåí÷àòàÿ ôóíêöèÿ
îáðàùàåòñÿ â íóëü ïðè îòðèöàòåëüíûõ çíà÷åíèÿõ åå àðãóìåíòà, ò.å.
ïðè n < N. Èç òåîðåìû çàäåðæêè â ÷àñòíîñòè ñëåäóåò, ÷òî ñäâèã
äèñêðåòíîãî ñèãíàëà íà îäèí èíòåðâàë äèñêðåòèçàöèè T ñîîòâåòñò-
âóåò óìíîæåíèþ z-ïðåîáðàçîâàíèÿ íà îïåðàòîð z
$
1
, ïîýòîìó ÷àñòî
z
$
1
íàçûâàþò îïåðàòîðîì åäèíè÷íîé çàäåðæêè â z-îáëàñòè.
Òåîðåìà óìíîæåíèÿ íà a
k
. Ìàòåìàòè÷åñêàÿ çàïèñü òåîðåìû
èìååò âèä
( )
(
)
1k
axkXaz
-
.
Òåîðåìà óìíîæåíèÿ íà k
( )
(
)
dXz
kxkz
dz
×- .
Òåîðåìû óìíîæåíèÿ äèñêðåòíîãî ñèãíàëà x(k) íà a
k
è íà k
ìîæíî òàêæå äîêàçàòü, èñïîëüçóÿ ôîðìóëó (19.29). Ïðåäëàãàåì
ïðîäåëàòü ýòî ñàìîñòîÿòåëüíî.
Òåîðåìà ñâåðòêè. Ñâåðòêå äèñêðåòíûõ ñèãíàëîâ x(k) è h(k)
ñîîòâåòñòâóåò ïðîèçâåäåíèå èõ z-ïðåîáðàçîâàíèé
( ) ( ) ( ) ( ) ( ) ( )
( ) ( )
¥¥
==
*=×-=×-×
åå
00kk
xkhkxkhmkhkxmkXzHz
.
Ýòó òåîðåìó ìû ïðèâîäèì çäåñü áåç äîêàçàòåëüñòâà. Ïðè íåîá-
õîäèìîñòè ñ íèì ìîæíî ïîçíàêîìèòüñÿ â ñïåöèàëüíîé ëèòåðàòóðå.
536
Ïðèìåð. Íàéäåì z-ïðåîáðàçîâàíèå ôóíêöèè åäèíè÷íîãî îòñ÷åòà, çàäåð-
æàííîé íà N èíòåðâàëîâ äèñêðåòèçàöèè.
Íàéäåì z-ïðåîáðàçîâàíèå äèñêðåòíîãî d-èìïóëüñà d(k) (ðèñ. 19.4), èñïîëü-
çóÿ âûðàæåíèå (19.29)
( )
( )
0
1
k
k
Xzkz
¥
-
d
=
=d=
å
.
Èñïîëüçóÿ òåîðåìó çàäåðæêè, íàéäåì z-èçîáðàæåíèå ñèãíàëà d(k $ N)
( ) ( )
NN
XzzXzz
--
d
=×=.
Íà ðèñóíêå 19.4 ïðèâåäåí òàêæå ãðàôèê çàäåðæàííîé ôóíêöèè åäèíè÷íî-
ãî îòñ÷åòà äëÿ ÷àñòíîãî ñëó÷àÿ N = 2.
Ïðèìåð. Íàéäåì z-ïðåîáðàçîâàíèå ôóíêöèè
( ) ( )
kN
xkaukN
-
=-
.
 îäíîì èç ïðèìåðîâ ìû óæå íàõîäèëè, ÷òî z-ïðåîáðàçîâàíèå ñèãíàëà a
k
èìååò âèä (19.34) X(z) = 1/(1 $ az
$1
).
Èñïîëüçóÿ òåîðåìó çàäåðæêè, ïîëó÷àåì
( )
1
1
N
kN
z
aukN
az
-
-
-
-
-
.
Ïðè a = 1 èìååì:
( )
-
-
-
-
1
1
N
z
ukN
z
.
Ãðàôèêè äèñêðåòíûõ ñèãíàëîâ u(k $ N) è a
k$ N
u(k $ N) ïðèâåäåíû íà
ðèñ. 19.24 è 19.25.
Ïðèìåð. Íàéäåì z-ïðåîáðàçîâàíèå äèñêðåòíîé ïîñëåäîâàòåëüíîñòè x(k) =
= ka
k
, k
0.
Ïîñêîëüêó z-èçîáðàæåíèå ïîñëåäîâàòåëüíîñòè a
k
èçâåñòíî (19.16), òî, èñ-
ïîëüçóÿ òåîðåìó óìíîæåíèÿ íà k, ïîëó÷èì
( )
( )
1
12
1
1
1
1
daz
Xzz
dz
az
az
-
-
-
æö
=-=
ç÷
-
èø
-
.
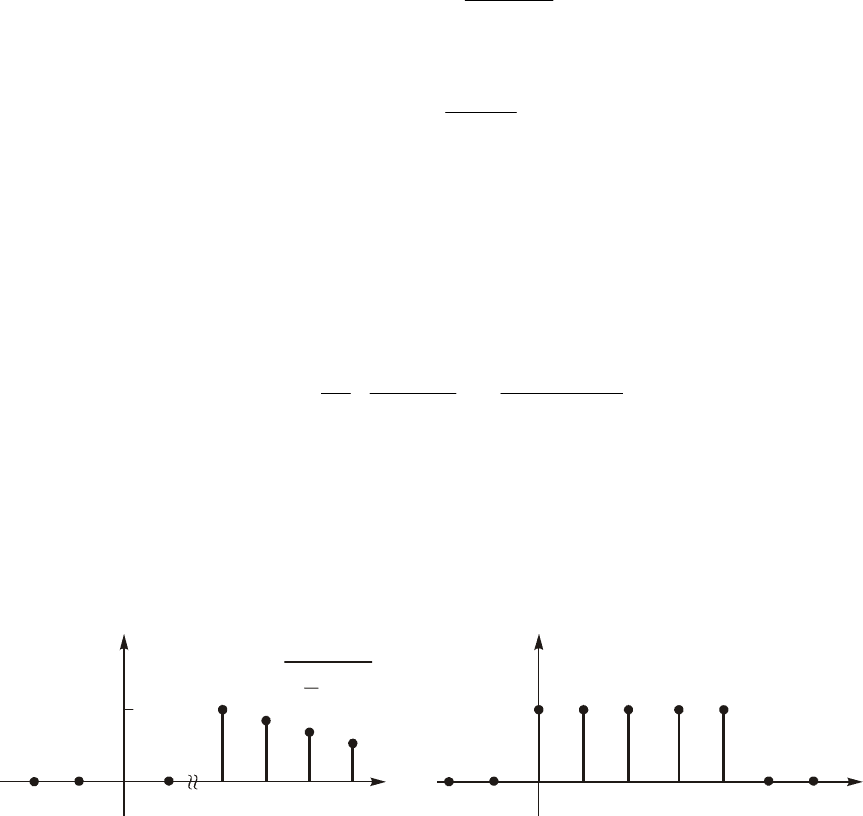
Ïðèìåð. Íàéäåì z-ïðåîáðàçîâàíèå äèñêðåòíîé ïîñëåäîâàòåëüíîñòè èç N
îòñ÷åòîâ åäèíè÷íîé àìïëèòóäû (ðèñ. 19.26)
( )
{
1,0,
0,.
kN
xk
kN
<
=
0
1
1
_
1
_
2
N
_
1
N
+1
N
k
auk
_
N
k
_
N
()
()
1
N
1
-
-
=
az
z
zX
0
1
2
1
_
1
_
2
N
_
1
N
+
1
N
k
xk
()
~
~
Ðèñ. 19.25 Ðèñ. 19.26

537
Ñèãíàë x(k) ìîæíî ïðåäñòàâèòü êàê ðàçíîñòü äâóõ ñèãíàëîâ
(
)
(
)
(
)
xkukukN
=--.
Èç òåîðåì ëèíåéíîñòè è çàäåðæêè ëåãêî ïîëó÷èòü z-ïðåîáðàçîâàíèå
( )
1
1
1
N
z
Xz
z
-
-
-
=
-
,
÷òî ñîâïàäàåò ñ ôîðìóëîé äëÿ ÷àñòè÷íîé ñóììû ãåîìåòðè÷åñêîé ïðîãðåññèè
( )
( )
1
00
N
kk
kk
Xzxkzz
¥-
--
==
==
åå
.
Ïðèìåð. Âû÷èñëèì z-ïðåîáðàçîâàíèå ñâåðòêè äèñêðåòíûõ ñèãíàëîâ x{k} =
= {1; 1; 1; 0; 0; 0; ...} è y{k} = {0; 0; 1; 1; 0; 0; ...}.
Íàéäåì z-ïðåîáðàçîâàíèå ñèãíàëà x(k), èñïîëüçóÿ ôîðìóëó (19.29)
( )
( )
¥
-
=
--
==
=++
å
0
12
1.
k
k
Xzxkz
zz
Íàéäåì z-ïðåîáðàçîâàíèå ñèãíàëà y(k)
( )
( )
23
0
k
k
Yzykzzz
¥
---
=
==+
å
.
Âû÷èñëèì z-ïðåîáðàçîâàíèå ñâåðòêè ñèãíàëîâ x(k) è y(k), èñïîëüçóÿ òåî-
ðåìó ñâåðòêè
( ) ( ) ( ) ( )
(
)
(
)
----
----
*×=+++=
=+++
1223
2345
1
22.
xnynXzYzzzzz
zzzz
 òàáë. 19.1 äàíà ñâîäêà z-ïðåîáðàçîâàíèé íàèáîëåå ÷àñòî âñòðå-
÷àþùèõñÿ äèñêðåòíûõ ïîñëåäîâàòåëüíîñòåé. Ýòè òàáëè÷íûå ñâåäåíèÿ
òàêæå ìîãóò áûòü èñïîëüçîâàíû äëÿ ðàñ÷åòà z-ïðåîáðàçîâàíèé ñèãíà-
ëîâ è ïåðåõîäà îò z-ïðåîáðàçîâàíèé ê äèñêðåòíûì ñèãíàëàì.
Ïðèìåð. Íàéäåì îáùèé ÷ëåí äèñêðåòíîãî ñèãíàëà x(k), êîòîðîìó ñîîòâåò-
ñòâóåò z-èçîáðàæåíèå
( )
12
12
11
11
1
66
zz
Xz
zz
--
--
--
=
--
.
Ðàçëîæåíèå ôóíêöèè X(z) íà ïðîñòûå äðîáè ïðèâîäèò ê âûðàæåíèþ
( )
11
32
6
11
11
23
Xz
zz
--
=++
-+
.
Èñïîëüçóÿ òåîðåìó ëèíåéíîñòè è íàõîäÿ â òàáëèöå 19.1 äèñêðåòíûå ñèãíà-
ëû, ñîîòâåòñòâóþùèå êàæäîìó èç ñëàãàåìûõ â âûðàæåíèè X(z), ïîëó÷àåì
( ) ( )
( ) ( )
( ) ( )
11,0,
6312213
312213,0.
kk
kk
k
xkk
k
=
ì
=d++-=
í
+->
î
538
Òàáë. 19.1 $ Êðàòêàÿ òàáëèöà îäíîñòîðîííèõ z-ïðåîáðàçîâàíèé
Äèñêðåòíûé ñèãíàë
x(k), k
0
z-ïðåîáðàçîâàíèå
( )
( )
0
k
k
Xzxkz
¥
-
=
=
å
( ) ( )
{
1,0
0,0
k
xkk
k
=
=d=
¹
(
)
1
Xz
=
( ) ( )
{
1,0
0,
kN
xkukN
kN
=-=
<
( )
1
1
N
z
Xz
z
-
-
=
-
( )
k
xka
=
( )
1
1
1
Xz
az
-
=
-
(
)
xkA
=
( )
1
1
1
Xz
z
-
=
-
(
)
xkk
=
( )
( )
1
2
1
1
z
Xz
z
-
-
=
-
( )
k
xkka
=
( )
( )
1
2
1
1
az
Xz
az
-
-
=
-
( )
cos
k
xkak
=q
( )
1
122
1cos
12cos
az
Xz
azaz
-
--
-q
=
-q+
()
sin
k
xkak
=q
( )
1
122
sin
12cos
az
Xz
azaz
-
--
q
=
-q+
()
2
,0
0,0
jkfT
ek
xk
k
p
ì
=
í
<
î
( )
21
1
1
jfT
Xz
ez
p-
=
-×
Ïî ýòîé ôîðìóëå ëåãêî ïîäñ÷èòàòü çíà÷åíèå x(k)äëÿ ëþáîãî k. Àíàëîãè÷íûì
îáðàçîì, ðàçëîæåíèå
( )
12
1
11
13
2
11
zz
Xzz
zz
--
-
--
++
==--+
--
ïðèâîäèò ê ïîñëåäîâàòåëüíîñòè
( ) ( ) ( )
1,0,
1232,1,
3,1.
k
xkkkk
k
=
ì
ï
=-d--d+==
í
ï
>
î
19.4. Äèñêðåòíûå öåïè
Äèñêðåòíàÿ ñâåðòêà. Â ïðåäûäóùèõ ðàçäåëàõ ýòîé ãëàâû áàëà
óñòàíîâëåíà îïðåäåëåííàÿ àíàëîãèÿ ìåæäó ñîîòíîøåíèÿìè, ñóùåñò-
âóþùèìè äëÿ àíàëîãîâûõ è äèñêðåòíûõ ñèãíàëîâ. Ïîäîáíàÿ àíàëî-
ãèÿ ñóùåñòâóåò è ìåæäó ìåòîäàìè àíàëèçà è ñèíòåçà àíàëîãîâûõ è
äèñêðåòíûõ öåïåé.

539
Ïîä äèñêðåòíîé öåïüþ ïîíèìàþò ëþáîå
óñòðîéñòâî, êîòîðîå ïðåîáðàçóåò îäíó ïî-
ñëåäîâàòåëüíîñòü x{k} â äðóãóþ y{k} (ðèñ.
19.27).
Ëèíåéíîé äèñêðåòíîé öåïüþ íàçûâàþò öåïü,
ïîä÷èíÿþùóþñÿ ïðèíöèïó ñóïåðïîçèöèè.
Ñâÿçü ìåæäó âõîäíûì äèñêðåòíûì ñèãíàëîì x{k } (âîçäåéñòâè-
åì) è âûõîäíûì ñèãíàëîì y{ k} (îòñ÷åòîì) îïðåäåëÿåòñÿ äèñêðåò-
íîé ñâåðòêîé (ñðàâíè ñ (8.12)):
( )
( ) ( ) ( ) ( )
,
kk
ynxkhnkhkxnk
¥¥
=-¥=-¥
=-=-
åå
(19.36)
ãäå h(k) $ èìïóëüñíàÿ õàðàêòåðèñòèêà äèñêðåòíîé öåïè. Îíà îï-
ðåäåëÿåòñÿ êàê îòêëèê äèñêðåòíîé öåïè íà âîçäåéñòâèå â âèäå åäè-
íè÷íîãî èìïóëüñà (d-ôóíêöèÿ, ðèñ. 19.4).
Èíîãäà ñâåðòêó (19.36) çàïèñûâàþò ñèìâîëè÷åñêè: y(k) = x(k)*
*h(k) (ñì. òåîðåìó ñâåðòêè, § 19.3).
Ëèíåéíàÿ äèñêðåòíàÿ öåïü, áóäåò óñòîé÷èâà, åñëè âûïîëíÿåòñÿ
óñëîâèå
( )
2
.
k
hk
¥
=-¥
<¥
å
(19.37)
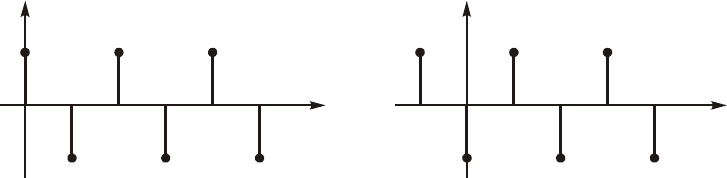
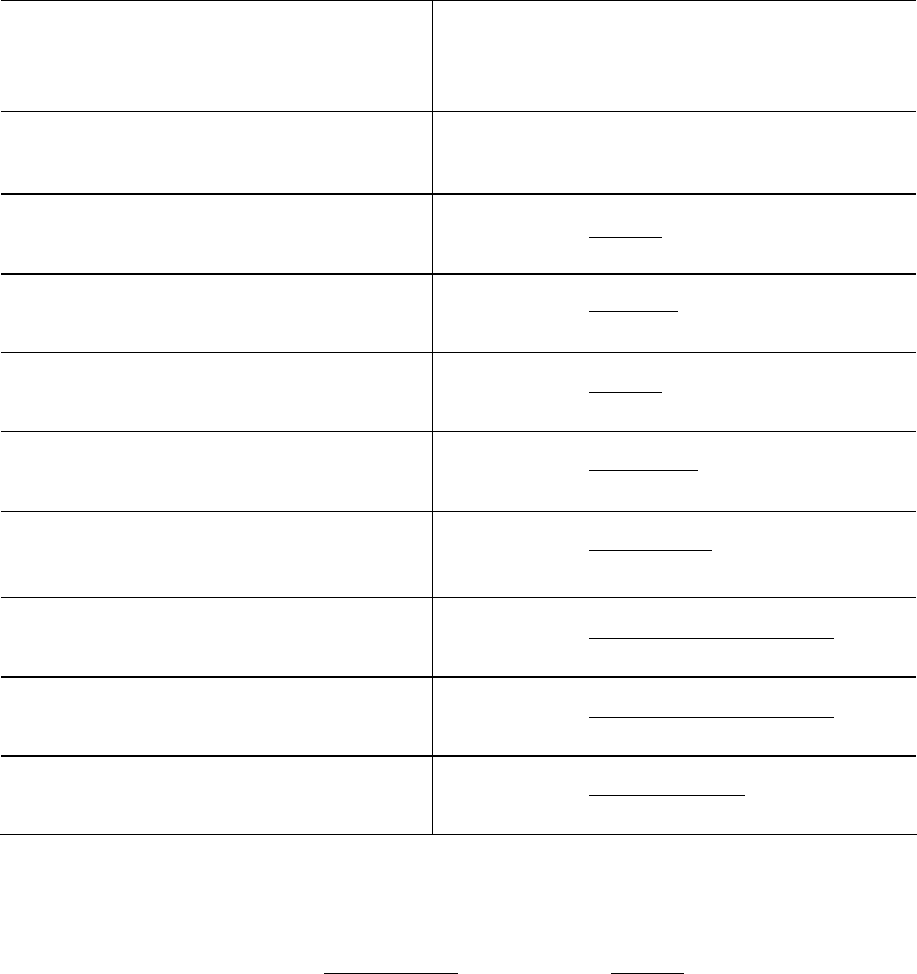
Ïðèìåð. Ðàññ÷èòàåì çíà÷åíèÿ âûõîäíîé ïîñëåäîâàòåëüíîñòè y{ k } öåïè,
èìåþùåé äèñêðåòíóþ èìïóëüñíóþ õàðàêòåðèñòèêó h{k} = {$1; 1; 2}, åñëè
âõîäíàÿ ïîñëåäîâàòåëüíîñòü èìååò âèä x{ k } = {$2; 1; 2: $1}. Ãðàôèêè x(k) è
h(k) ïðèâåäåíû íà ðèñ. 19.28.
Ïîëüçóÿñü ôîðìóëîé (19.36), ðàññ÷èòàåì çíà÷åíèÿ âûõîäíîé ïîñëåäîâà-
òåëüíîñòè y(k)
(
)
(
)
(
)
(
)
(
)
()
( )
() ()
( )
( ) ( )
=×=-×-=
=×+×=-×+×-=-
××××××××××××××××××××××××××××
000122,
1011011123,
yhx
yhxhx
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
( ) ( ) ( )
=×+×+×+×+×=
=-×+×-+×+×+×-=
××××××××××××××××××××××××××××
40413223140
10112201023,
yhxhxhxhxhx
Ãðàôèê äèñêðåòíîãî ñèãíàëà y(k) ïðèâåäåí íà ðèñ. 19.29.
0
0
1
1
1
1
2
2
_
1
_
1
_
1
_
1
_
2
_
2
_
2
2
2
3
3
4
4
5
5
6
6
k
k
xk
()
hk
()
Ðèñ. 19.28
xk
{}
yk
{}
hk
{}
Ðèñ. 19.27
540
0
1
1
2
3
4
5
_
1
_
1
_
2
_
2
_
3
_
4
_
5
2
3
4
5
6
7
8
9
10
11
k
yk
()
Ðèñ. 19.29
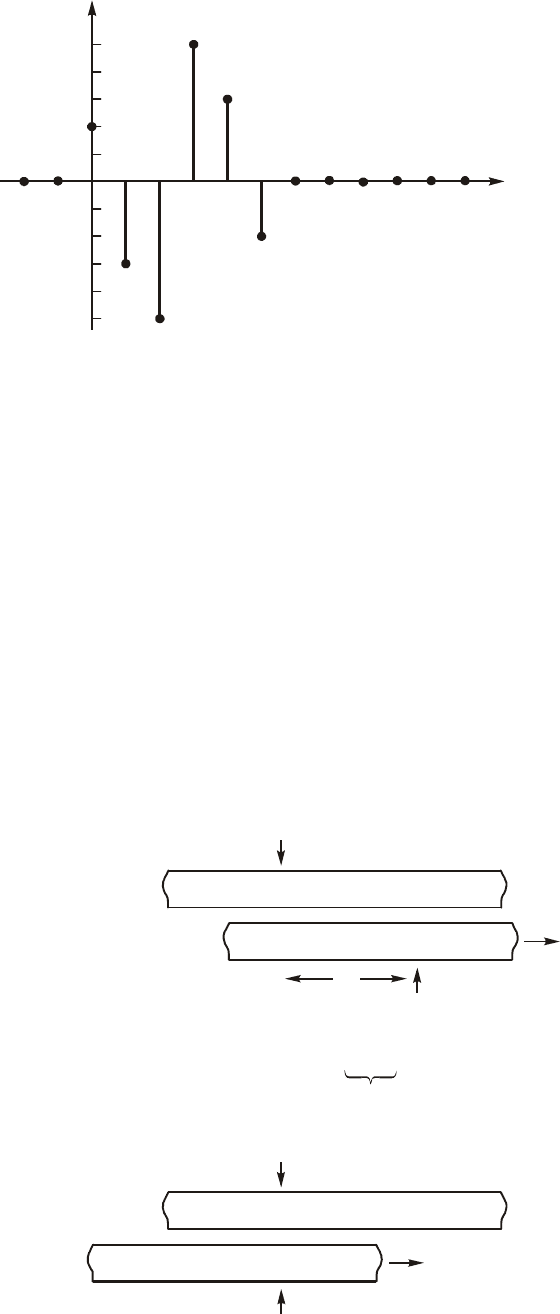
Âû÷èñëåíèÿ ïî ôîðìóëå (19.36) ìîæíî âûïîëíèòü òàêæå ñ ïîìîùüþ ïðî-
ñòîãî óñòðîéñòâà. Çàïèøåì ïîñëåäîâàòåëüíîñòè ÷èñåë x(k) è h($k) íà îòäåëü-
íûõ ïîëîñêàõ áóìàãè, êàê ïîêàçàíî íà ðèñ. 19.30. Íà îáåèõ ïîëîñêàõ ïîìåòèì
ìàëåíüêèìè ñòðåëî÷êàìè òî÷êè k = 0. Îáðàòèì âíèìàíèå íà òî, ÷òî h($k) ÿâ-
ëÿåòñÿ îáðàòíîé ïîñëåäîâàòåëüíîñòüþ îòíîñèòåëüíî h(k), òàê ÷òî îíà ñòðîèòñÿ
â îáðàòíîì íàïðàâëåíèè îò k = 0. Áóäåì ñäâèãàòü íèæíþþ ïîëîñêó îòíîñè-
òåëüíî âåðõíåé â íàïðàâëåíèè ñòðåëêè. Âû÷èñëåíèå ñóììû ïðîèçâåäåíèé ñòîÿ-
ùèõ äðóã ïðîòèâ äðóãà ÷èñåë ïðè êàæäîì ñäâèãå äàåò ïîñëåäîâàòåëüíîñòü y(k).
Ïðîâåäÿ äèñêðåòèçàöèþ èìïóëüñíîé õàðàêòåðèñòèêè àíàëîãîâîé
öåïè ìîæíî îïèñàòü åå äèñêðåòíîé ìàòåìàòè÷åñêîé ìîäåëüþ. Åñëè,
íàïðèìåð, äëÿ RC-öåïè, èçîáðàæåííîé íà ðèñ. 19.31 âçÿòü äèñ-
êðåòíûå çíà÷åíèÿ èìïóëüñíîé õàðàêòåðèñòèêè:
xk
()
xk
()
hk
()
_
hk
()
_
0
0
0
0
0
0
0
0
0
0
_
2
_
2
0
0
0
0
1
1
0
0
0
0
2
2
2
2
4
2
3
2
Ïðîèçâåäåíèå
Ïðîèçâåäåíèå
Ñóììà ïðîèçâåäåíèé
=
Ñóììà ïðîèçâåäåíèé
=
= (4)
y
= (0)
y
_
1
_
1
1
1
_
1
0
0
0
_
1
_
1
0
0
0
0
0
0
0
0
0
0
0
0
k
= 0
k
= 0
n
= 0
k
= 0
4
Ðèñ. 19.30
