Бакалов В.П. Основы теории цепей. 3-е издание

Подождите немного. Документ загружается.

101

Ðèñ. 3.30

ãäå k

òð

= L

/M êîýôôèöèåíò

òðàíñôîðìàöèè. Êàê âèäíî, â

äàííîì ñëó÷àå îòíîøåíèå íàï-

ðÿæåíèé íå çàâèñèò îò íàãðóçêè,

à îòíîøåíèå òîêîâ çàâèñèò îò

. Òàêîé òðàíñôîðìàòîð íàçû-

âàþò ñîâåðøåííûì. Äëÿ íåãî êî-

ýôôèöèåíò ñâÿçè k = 1, à êîýô-

ôèöèåíò ðàññåÿíèÿ s = 0.

Ñóùåñòâóåò åùå ïîíÿòèå

èäåàëüíîãî òðàíñôîðìàòîðà, ó êîòîðîãî ïîòåðè ðàâíû íóëþ,

èíäóêòèâíîñòè êàòóøåê áåñêîíå÷íî âåëèêè, à èõ îòíîøåíèå ðàâ-

íî êîýôôèöèåíòó òðàíñôîðìàöèè k

òð

= L

= w

, ãäå w

÷èñëî âèòêîâ ïåðâè÷íîé è âòîðè÷íîé êàòóøåê. Â èäåàëüíîì

òðàíñôîðìàòîðå îòíîøåíèå êàê òîêîâ, òàê è íàïðÿæåíèé íå çàâè-

ñèò îò íàãðóçêè è îïðåäåëÿþòñÿ òîëüêî êîýôôèöèåíòîì òðàíñ-

ôîðìàöèè k

òð

Òðàíñôîðìàòîð ñ ôåððîìàãíèòíûì ñåðäå÷íèêîì. Ôåððîìàãíèò-

íûé ñåðäå÷íèê ïðèìåíÿåòñÿ äëÿ óâåëè÷åíèÿ ìàãíèòíîãî ïîòîêà è

ñâÿçè ìåæäó êàòóøêàìè, ÷òî ïðèâîäèò ê ðîñòó ìîùíîñòè, îòäàâàå-

ìîé âî âòîðè÷íóþ öåïü òðàíñôîðìàòîðà. Ïðè ýòîì ïî ñâîèì ñâîé-

ñòâàì îí ïðèáëèæàåòñÿ ê èäåàëüíîìó òðàíñôîðìàòîðó, íî ñòàíî-

âèòñÿ â îáùåì ñëó÷àå íåëèíåéíûì óñòðîéñòâîì âñëåäñòâèå ïîÿâ-

ëåíèÿ äîïîëíèòåëüíûõ ïîòåðü íà ãèñòåðåçèñ è âèõðåâûå òîêè. Îä-

íàêî íà ïðàêòèêå òðàíñôîðìàòîð ñ ôåððîìàãíèòíûì ñåðäå÷íè-

êîì ñòàðàþòñÿ êîíñòðóèðîâàòü òàêèì îáðàçîì, ÷òîáû íåëèíåéíîñòü

áûëà ìàëà è åþ ìîæíî áûëî ïðåíåáðå÷ü. Òîãäà ðàñ÷åò ïîäîáíîãî

òðàíñôîðìàòîðà ìîæíî îñóùåñòâèòü íà îñíîâå äâóõêîíòóðíîé ñõå-

ìû çàìåùåíèÿ, èçîáðàæåííîé íà ðèñ. 3.30 ñ ïàðàìåòðàìè, ïðèâå-

äåííûìè ê ïàðàìåòðàì ïåðâè÷íîé îáìîòêè. Äàííàÿ ñõåìà ìîæåò

áûòü ïîëó÷åíà ïî àíàëîãèè ñî ñõåìîé ðèñ. 3.28 ñ ó÷åòîì ïîòåðü â

ñòàëè G

è íàìàãíè÷èâàíèÿ Â

. Ïðèâåäåííûå çíà÷åíèÿ Õ¢

, I¢

îï-

ðåäåëÿþòñÿ ñîãëàñíî ðàâåíñòâàì:

¢¢

====

2òð22òð2òðòð

òð

;;;;

XkXRkRIIkUkU

ZkZ

(3.115)

ãäå Õ

, Õ

$ èíäóêòèâíûå ñîïðîòèâëåíèÿ ïåðâè÷íîé è âòîðè÷íîé

êàòóøåê (èíäóêòèâíîñòè ðàññåÿíèÿ). Âåëè÷èíû òîêà ïîòåðü â ñòàëè

= G

è íàìàãíè÷èâàþùåãî òîêà I

= B

îïðåäåëÿþò ñóì-

ìàðíûé òîê ïîòåðü:

=+=

ôí0

IIjIIe

, (3.116)

ãäå àðãóìåíò d íàçûâàåòñÿ óãëîì ïîòåðü.

102

3.10. Áàëàíñ ìîùíîñòè

Ïðåäñòàâèì ïàññèâíóþ ýëåêòðè÷åñêóþ öåïü, íàõîäÿùóþñÿ ïîä

âîçäåéñòâèåì èñòî÷íèêà ãàðìîíè÷åñêîãî íàïðÿæåíèÿ, â ôîðìå

äâóõïîëþñíèêà (ñì. ðèñ. 1.1). Ïîä âîçäåéñòâèåì íàïðÿæåíèÿ è

àb

= U

sinwt â öåïè ïðîòåêàåò òîê i = I

sin(wt $ j). Îòäàâàåìàÿ èñ-

òî÷íèêîì â öåïü çà ïåðèîä Ò ñðåäíÿÿ ìîùíîñòü

===j=j

ñð

coscos

PPuidtUI

. (3.117)

Ñîãëàñíî çàêîíó Îìà U = ZI èëè ñ ó÷åòîì (3.35) U = RI/cosj.

Òîãäà óðàâíåíèå (3.117) ïðèíèìàåò âèä

PIRUG

. (3.118)

Òàêèì îáðàçîì, ñðåäíÿÿ çà ïåðèîä ìîùíîñòü Ð ðàâíà ìîùíîñòè,

ðàññåèâàåìîé íà ðåçèñòèâíîì ñîïðîòèâëåíèè (ïðîâîäèìîñòè) öåïè.

Â ýòîé ñâÿçè ìîùíîñòü Ð íîñèò íàçâàíèå àêòèâíîé è èçìåðÿåòñÿ â

âàòòàõ (Âò).

Êðîìå àêòèâíîé ìîùíîñòè Ð â öåïÿõ ãàðìîíè÷åñêîãî òîêà èñ-

ïîëüçóþò ïîíÿòèå ðåàêòèâíîé ìîùíîñòè

=j==

sin

QUIIXUB

(3.119)

è êîìïëåêñíîé ìîùíîñòè

SPjQ

. (3.120)

Ìîäóëü êîìïëåêñíîé ìîùíîñòè íàçûâàåòñÿ ïîëíîé ìîùíîñòüþ:

==+

SPQ

. (3.121)

Åäèíèöà èçìåðåíèÿ ðåàêòèâíîé ìîùíîñòè $ ÂÀð, à ïîëíîé $ âîëüò-

àìïåð (Â×À).

Ìîùíîñòè P, Q, S ìîæíî âûðàçèòü è â äðóãîé ôîðìå. Ïðåä-

ñòàâèì S ñ ó÷åòîì (3.117) è (3.119) â âèäå

=j+j==

cossin

SUIjUIUIeUI

. (3.122)

Òîãäà íåòðóäíî âèäåòü, ÷òî

======

Re[]Re[];Im[]Im[];PUISQUISSUI

(3.123)

ò. å. àêòèâíàÿ ìîùíîñòü ðàâíà ðåàëüíîé ÷àñòè, à ðåàêòèâíàÿ $

ìíèìîé ÷àñòè êîìïëåêñíîé ìîùíîñòè S. Êàê ñëåäóåò èç ôîðìóë

(3.117) è (3.123):

cos

. (3.124)

Ýòî îòíîøåíèå â ýíåðãåòèêå íàçûâàåòñÿ êîýôôèöèåíòîì ìîù-

íîñòè (êîñèíóñîì j) è ÿâëÿåòñÿ âàæíîé õàðàêòåðèñòèêîé ýëåêòðè-

÷åñêèõ ìàøèí è ëèíèé ýëåêòðîïåðåäà÷è. ×åì âûøå cos j, òåì

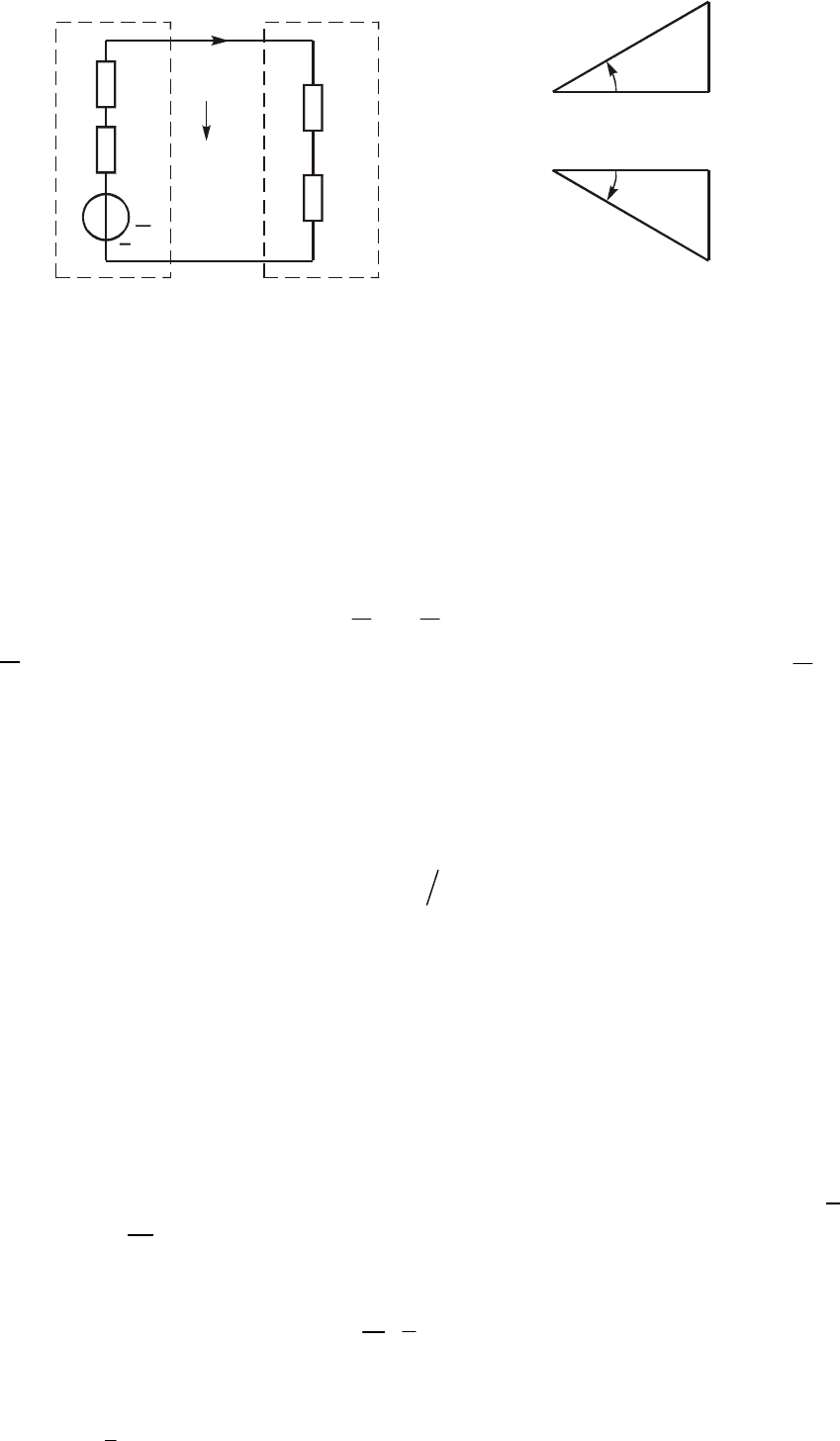
103

)

Ðèñ. 3.31 Ðèñ. 3.32

ìåíüøå ïîòåðè ýíåðãèè â ëèíèè è âûøå ñòåïåíü èñïîëüçîâàíèÿ

ýëåêòðè÷åñêèõ ìàøèí è àïïàðàòîâ. Ìàêñèìàëüíîå çíà÷åíèå

cos j = l, ïðè ýòîì Ð = S, Q = 0, ò. å. öåïü íîñèò ÷èñòî àêòèâíûé

õàðàêòåð è ñäâèã ôàç ìåæäó òîêîì i è íàïðÿæåíèåì è ðàâåí íóëþ.

Óñëîâèå ïåðåäà÷è ìàêñèìàëüíîé ìîùíîñòè îò ãåíåðàòîðà â íà-

ãðóçêó ìîæíî íàéòè èç óñëîâèÿ

ã í

, (3.125)

ãäå Z

$ êîìïëåêñíîå âíóòðåííåå ñîïðîòèâëåíèå èñòî÷íèêà;

êîìïëåêñíî-ñîïðÿæåííîå ñîïðîòèâëåíèå íàãðóçêè. Ýòî óñëîâèå

ñëåäóåò íåïîñðåäñòâåííî èç ðàññìîòðåíèÿ ýêâèâàëåíòíîé ñõåìû,

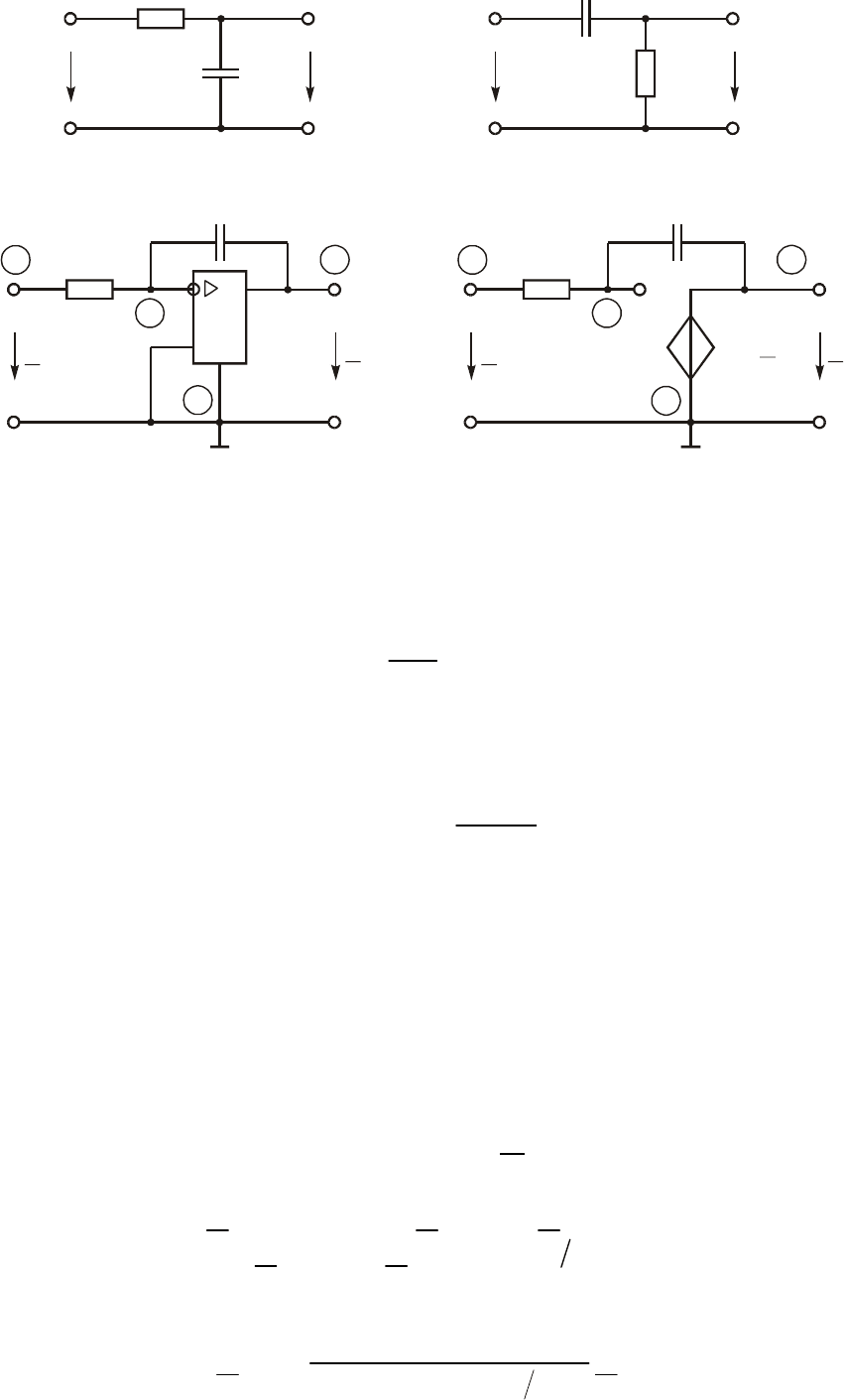
ïðèâåäåííîé íà ðèñ. 3.31. Òîê â äàííîé öåïè äîñòèãàåò ìàêñèìóìà

ïðè Õ

= $Õ

è âûïîëíåíèè óñëîâèÿ R

= R

(ñì. § 2.6), ÷òî è äî-

êàçûâàåò ðàâåíñòâî (3.125). Ïðè ýòîì ìîùíîñòü â íàãðóçêå áóäåò

îïðåäåëÿòüñÿ óðàâíåíèåì

í ãã

PUR

. (3.126)

Ïî àíàëîãèè ñ òðåóãîëüíèêàìè òîêîâ è íàïðÿæåíèé, ñîïðîòèâ-

ëåíèé è ïðîâîäèìîñòåé (§§ 3.4 è 3.5) ìîæíî ââåñòè òðåóãîëüíèêè

ìîùíîñòåé. Òàê ñîãëàñíî (3.121) è (3.122) òðåóãîëüíèê ìîùíîñòåé

äëÿ öåïè, íîñÿùèé èíäóêòèâíûé õàðàêòåð áóäåò èìåòü âèä, èçî-

áðàæåííûé íà ðèñ. 3.32, à, à äëÿ öåïè ñ åìêîñòíûì õàðàêòåðîì $

íà ðèñ. 3.32, á.

Ðàññìîòðèì óñëîâèå áàëàíñà ìîùíîñòè â öåïÿõ ïðè ãàðìîíè-

÷åñêîì âîçäåéñòâèè. Â ñèëó ñïðàâåäëèâîñòè ïåðâîãî è âòîðîãî çà-

êîíîâ Êèðõãîôà äëÿ êîìïëåêñíûõ äåéñòâóþùèõ çíà÷åíèé òîêà I è

íàïðÿæåíèé U â êàæäîé èç âåòâåé ðàññìàòðèâàåìîé öåïè ìîæíî

çàïèñàòü òåîðåìó Òåëëåäæåíà (1.35) â êîìïëåêñíîé ôîðìå:

UI . (3.127)

Îäíàêî ïîñêîëüêó ÇÒÊ ñïðàâåäëèâ è ïî îòíîøåíèþ ê ñîïðÿæåí-

íûì òîêàì

, òî óðàâíåíèå (3.127) ìîæíî çàïèñàòü â âèäå

104

åå

UIS. (3.128)

Óðàâíåíèå (3.128) îòðàæàåò áàëàíñ êîìïëåêñíîé ìîùíîñòè, ñî-

ãëàñíî êîòîðîìó ñóììà êîìïëåêñíûõ ìîùíîñòåé, ïîòðåáëÿåìûõ

âñåìè âåòâÿìè öåïè, ðàâíà íóëþ. Áàëàíñ êîìïëåêñíîé ìîùíîñòè

ìîæíî ñôîðìóëèðîâàòü è â äðóãîé ôîðìå: ñóììà êîìïëåêñíûõ

ìîùíîñòåé, îòäàâàåìûõ íåçàâèñèìûìè èñòî÷íèêàìè, ðàâíà ñóììå

êîìïëåêñíûõ ìîùíîñòåé, ïîòðåáëÿåìûõ îñòàëüíûìè âåòâÿìè ýëåê-

òðè÷åñêîé öåïè:

åå

èñòïîò

SS. (3.129)

Èç óñëîâèÿ áàëàíñà êîìïëåêñíîé ìîùíîñòè ñëåäóþò óñëîâèÿ

áàëàíñà àêòèâíûõ è ðåàêòèâíûõ ìîùíîñòåé:

åå

èñòïîò

PP; (3.130)

åå

èñòïîò

QQ. (3.131)

Óñëîâèå áàëàíñà àêòèâíûõ ìîùíîñòåé íåïîñðåäñòâåííî âûòåêàåò èç

çàêîíà ñîõðàíåíèÿ ýíåðãèè.

3.11. Ìîäåëè ýëåêòðè÷åñêèõ öåïåé ñ çàâèñèìûìè

èñòî÷íèêàìè

Èíòåãðèðóþùèå è äèôôåðåíöèðóþùèå öåïè. Èíòåãðèðóþùèå

è äèôôåðåíöèðóþùèå öåïè íàõîäÿò øèðîêîå ïðèìåíåíèå â ðàç-

ëè÷íûõ óñòðîéñòâàõ èìïóëüñíîé è âû÷èñëèòåëüíîé òåõíèêè äëÿ

ôîðìèðîâàíèÿ ëèíåéíî èçìåíÿþùèõñÿ íàïðÿæåíèé è òîêîâ, ñåëåê-

öèè ñèãíàëîâ, ëèíåéíîãî ïðåîáðàçîâàíèÿ ðàçëè÷íûõ èìïóëüñîâ è

ò. ä. Èíòåãðèðóþùàÿ öåïü îïèñûâàåòñÿ óðàâíåíèåì

211

()()

ftkftdt

, (3.132)

à äèôôåðåíöèðóþùàÿ $ óðàâíåíèåì

()

dft

ftk

, (3.133)

ãäå k

, k

$ êîýôôèöèåíòû ïðîïîðöèîíàëüíîñòè.

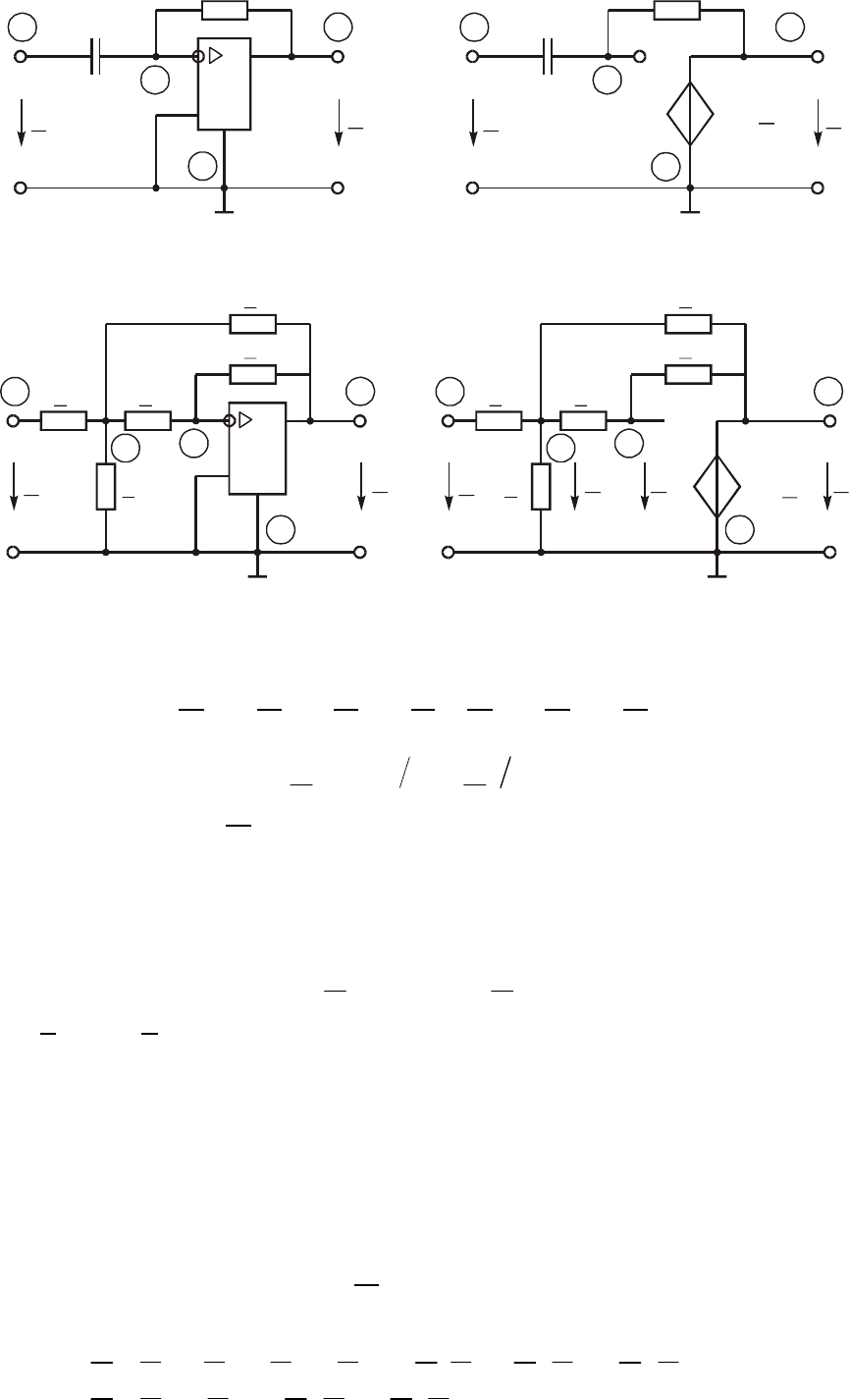
Ïðîñòåéøàÿ èíòåãðèðóþùàÿ è äèôôåðåíöèðóþùàÿ öåïè ìîãóò

áûòü ðåàëèçîâàíû íà áàçå RÑ-öåïî÷êè (ðèñ. 3.33, 3.34). Äåéñòâè-

òåëüíî, åñëè ïàðàìåòðû èíòåãðèðóþùåé öåïî÷êè (ðèñ. 3.33) òàêî-

105

âõ

âûõ

âõ

âûõ

Ðèñ. 3.33 Ðèñ. 3.34

)

-H

Ðèñ. 3.35

âû, ÷òî t = RÑ

, ãäå t

äëèòåëüíîñòü âõîäíîãî ñèãíàëà, òî íà

âûõîäå òàêîé öåïè èìååì

()()

ututdt

Àíàëîãè÷íî, åñëè äëÿ äèôôåðåíöèðóþùåé öåïî÷êè (ðèñ. 3.34) âû-

ïîëíåíî óñëîâèå t = RÑ

, òî

()

dut

utRC

. (3.134)

Îäíàêî òî÷íîñòü èíòåãðèðîâàíèÿ è äèôôåðåíöèðîâàíèÿ òàêîé ïàñ-

ñèâíîé öåïè íåâûñîêà. Ïîýòîìó íà ïðàêòèêå îïåðàöèè (3.132) è

(3.133) ðåàëèçóþò ñ ïîìîùüþ àêòèâíûõ öåïåé ñ çàâèñèìûìè èñ-

òî÷íèêàìè, íàïðèìåð íà áàçå ÎÓ.

Íà ðèñ. 3.35, à èçîáðàæåíà ñõåìà èíòåãðàòîðà, à íà ðèñ. 3.36, à $

äèôôåðåíöèàòîðà íà ÎÓ. Îïðåäåëèì êîìïëåêñíîå äåéñòâóþùåå

íàïðÿæåíèå íà âûõîäå èíòåãðàòîðà. Äëÿ ýòîãî âîñïîëüçóåìñÿ ýê-

âèâàëåíòíîé ñõåìîé çàìåùåíèÿ ÎÓ â âèäå ÈÍÓÍà (ðèñ. 3.35, á).

Ïðèíÿâ ïîòåíöèàë áàçèñíîãî óçëà V

= 0 ñîñòàâèì óðàâíåíèå

ðàâíîâåñèÿ óçëîâûõ ïîòåíöèàëîâ:

(

)

-w-=

=-=

321

, ãäå1.

VVjCVG

GjC

VHVGR

Îòêóäà, ïîñëå íåñëîæíûõ ïðåîáðàçîâàíèé ïîëó÷èì

+w+

(11)

GjCHH

106

1 2

)

-H

Ðèñ. 3.36

)

-H

Ðèñ. 3.37

Ó÷èòûâàÿ, ÷òî U

= V

$ V

= V

; U

$ U

= V

è äëÿ èäåàëüíî-

ãî ÎÓ Í

= ¥, îêîí÷àòåëüíî íàõîäèì

=-w

(1)

UjURC

. (3.135)

À òàê êàê äåëåíèå U

íà jw ñîîòâåòñòâóåò îïåðàöèè èíòåãðèðîâàíèÿ

âõîäíîãî ñèãíàëà u

(t) (ñì. § 3.6), òî ñõåìà, èçîáðàæåííàÿ íà

ðèñ. 3.34 ÿâëÿåòñÿ ìîäåëüþ èäåàëüíîãî èíòåãðàòîðà.

Àíàëîãè÷íî ìîæíî ïîëó÷èòü äëÿ èäåàëüíîãî äèôôåðåíöèàòîðà

(ñì. ðèñ. 3.36):

=-w

UjRCU

, (3.136)

ò. å. u

(t) è u

(t) ñâÿçàíû ìåæäó ñîáîé çàâèñèìîñòüþ, àíàëîãè÷íîé

(3.134). Çíàê «$» â óðàâíåíèè (3.135) è (3.136) îáóñëîâëåí ïîâî-

ðîòîì íà óãîë p ôàçû âõîäíîãî ñèãíàëà ïîäàííîãî íà èíâåð-

òèðóþùèé âõîä ÎÓ.

ARC-öåïü âòîðîãî ïîðÿäêà. Íà ðèñ. 3.37 èçîáðàæåíà àêòèâíàÿ

RC-öåïü (ARC-öåïü) âòîðîãî ïîðÿäêà, êîòîðàÿ íàõîäèò øèðîêîå

ïðèìåíåíèå â êà÷åñòâå òèïîâîãî çâåíà ðàçëè÷íûõ óñòðîéñòâ:

ôèëüòðîâ, êîððåêòîðîâ è äð. (ñì.ãë.14, 17, 18).

Ïðèíÿâ ïîòåíöèàë óçëà V

= 0 (áàçèñíûé óçåë) ñîñòàâèì äëÿ

óçëîâ 3 è 4 óðàâíåíèÿ ïî ìåòîäó óçëîâûõ ïîòåíöèàëîâ (ðèñ. 3.37, á):

+++---=

+--=

1234143

3124

3535

432

()0,

()0.

VYYYYVYVYVY

VYYVYVY

(3.137)

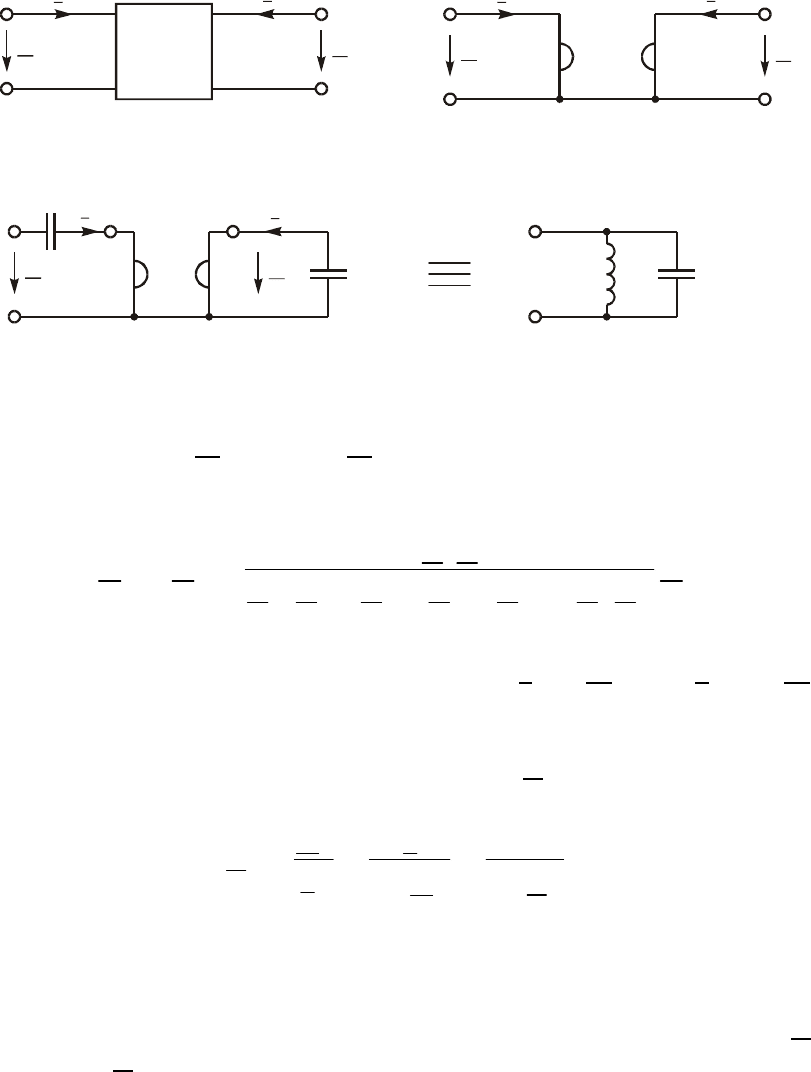
107

)

Ðèñ. 3.38

)

=Ñ/G

)

Ðèñ. 3.39

Ó÷èòûâàÿ, ÷òî V

= %H

è H

= ¥ (èäåàëüíûé ÎÓ) ïîñëå

ðåøåíèÿ ñèñòåìû óðàâíåíèé (3.137), ïîëó÷èì íàïðÿæåíèå íà âû-

õîäå:

++++

221

5123434

()

UVU

YYYYYYY

. (3.138)

Ãèðàòîð. Ãèðàòîðîì íàçûâàþò íåîáðàòèìûé ÷åòûðåõïîëþíèê

(ðèñ. 3.38, à), îïèñûâàåìûé óðàâíåíèÿìè I

= U

è I

= $U

ãäå G

ïðîâîäèìîñòü ãèðàòîðà.

Óñëîâíîå èçîáðàæåíèå ãèðàòîðà ïîêàçàíî íà ðèñ. 3.38, á. Íà-

ãðóçèì ãèðàòîð ñîïðîòèâëåíèåì íàãðóçêè Z

. Âõîäíîå ñîïðîòèâëå-

íèå ãèðàòîðà

===

ãã

GUGZ

, (3.139)

ò. å. îáðàòíî ñîïðîòèâëåíèþ íàãðóçêè, ïîýòîìó ãèðàòîð ÷àñòî íà-

çûâàþò èíâåðòîðîì ïîëîæèòåëüíîãî ñîïðîòèâëåíèÿ. Ñâîéñòâî

(3.139) ÿâëÿåòñÿ î÷åíü âàæíûì, ïîñêîëüêó ïîçâîëÿåò èìèòèðîâàòü

èíäóêòèâíîñòü ñ ïîìîùüþ åìêîñòè. Äåéñòâèòåëüíî, åñëè Z

= l/jwC, òî Z

= jwL

, ãäå L

= C/G

$ ýêâèâàëåíòíàÿ èíäóê-

òèâíîñòü. Ýòî ñâîéñòâî ãèðàòîðîâ ÿâëÿåòñÿ î÷åíü öåííûì äëÿ ìèê-

ðîýëåêòðîíèêè, ïîñêîëüêó èçãîòîâëåíèå èíäóêòèâíîñòåé ïî èíòåã-

ðàëüíîé òåõíîëîãèè ïðåäñòàâëÿåò ñëîæíóþ çàäà÷ó. Èñïîëüçîâàíèå

æå ãèðàòîðîâ ñ ìàëûì çíà÷åíèåì G

ïîçâîëÿåò èç íåáîëüøèõ åì-

êîñòåé Ñ ìîäåëèðîâàòü áîëüøèå çíà÷åíèÿ èíäóêòèâíîñòè L.

Ñóùåñòâóþò è äðóãèå ìíîãî÷èñëåííûå ïðèìåíåíèÿ ãèðàòîðà:

ïðåîáðàçîâàíèå íàïðÿæåíèÿ è òîêà, ìîäåëèðîâàíèå Ò- è Ï-îáðàç-

íûõ çâåíüåâ ñ êàòóøêàìè èíäóêòèâíîñòè, òðàíñôîðìàòîðîâ, ðåçî-

íàíñíûõ êîíòóðîâ. Â êà÷åñòâå ïðèìåðà íà ðèñ. 3.39 èçîáðàæåíà

ìîäåëü ïàðàëëåëüíîãî êîëåáàòåëüíîãî êîíòóðà (ðèñ. 3.39, á) íà áà-

çå ãèðàòîðà (3.39, à).

108

Ðèñ. 3.40

Âàæíûì ñâîéñòâîì ãèðàòîðà ÿâëÿåòñÿ òî, ÷òî îí íå âíîñèò ýíåð-

ãèè â öåïü è íå ïîòðåáëÿåò åå èç öåïè, ò. å. âåäåò ñåáÿ êàê ïàññèâ-

íûé ýëåìåíò áåç ïîòåðü. Ýòî ñëåäóåò íåïîñðåäñòâåííî èç óðàâíåíèé

ãèðàòîðà.

Ðåàëèçàöèÿ ãèðàòîðà îñóùåñòâëÿåòñÿ ñ èñïîëüçîâàíèåì àêòèâíûõ

ýëåìåíòîâ. Íàïðèìåð, ÎÓ (íà áàçå äâóõ èñòî÷íèêîâ ÈÒÓÍ: íà áàçå

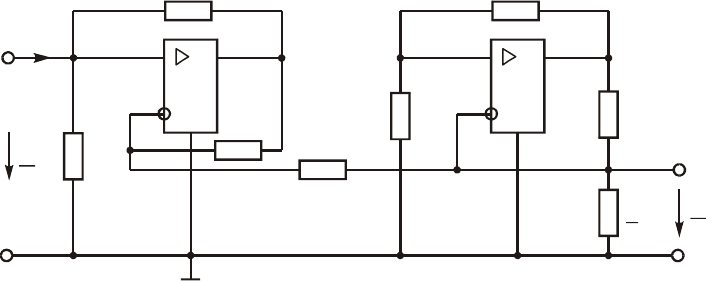
ÈÒÓÍ è ÎÎÑ; íà îñíîâå äâóõ ÏÎÑ è äð.). Íà ðèñ. 3.40 èçîáðàæå-

íà ñõåìà ãèðàòîðà ñ äâóìÿ ÈÒÓÍ, âûïîëíåííûìè íà áàçå ÎÓ.

Âîïðîñû è çàäàíèÿ äëÿ ñàìîïðîâåðêè

1. Â ÷åì ðàçëè÷èå ìåæäó ìãíîâåííûì çíà÷åíèåì ñèíóñîèäàëüíîãî

òîêà è åãî äåéñòâóþùèì çíà÷åíèåì?

2. Êàêîé ôîðìóëîé ñâÿçàíû ìåæäó ñîáîé àêòèâíàÿ, ðåàêòèâíàÿ ñî-

ñòàâëÿþùèå è êîìïëåêñíîå íàïðÿæåíèå?

3. Êàê îðèåíòèðîâàíû ìåæäó ñîáîé âåêòîðû òîêà è íàïðÿæåíèÿ íà

èíäóêòèâíîñòè (åìêîñòè)?

4. Ìîæåò ëè íàïðÿæåíèå íà èíäóêòèâíîñòè (åìêîñòè) â öåïî÷êå èç

ïîñëåäîâàòåëüíî ñîåäèíåííûõ RLC ïðåâûøàòü óðîâåíü ïðèëî-

æåííîãî íàïðÿæåíèÿ?

5. Äâå èíäóêòèâíîñòè L

= 5 ìÃí è L

= 15 ìÃí âêëþ÷åíû ïîñëå-

äîâàòåëüíî. Îïðåäåëèòü èõ ýêâèâàëåíòíîå ñîïðîòèâëåíèå íà

÷àñòîòå f = 1000 Ãö.

Îòâåò: Õ

= 125,6 Îì.

6. Â ñõåìå, èçîáðàæåííîé íà ðèñ. 3.7, U = 10 Â, ïàäåíèå íàïðÿ-

æåíèÿ íà èíäóêòèâíîñòè u

= 5 Â, íà åìêîñòè u

= 11 Â. Îïðå-

äåëèòü ïàäåíèå íàïðÿæåíèÿ íà ðåçèñòîðå u

Îòâåò: u

= 8 Â.

7. Âû÷èñëèòü ýêâèâàëåíòíîå ñîïðîòèâëåíèå äâóõ êîíäåíñàòîðîâ

= 5 ìêÔ è Ñ

= 15 ìêÔ, âêëþ÷åííûõ ïàðàëëåëüíî íà ÷àñòî-

òå f = 5 êÃö.

Îòâåò: Õ

= 1,59 Îì.

109

8. Àìïåðìåòð, âêëþ÷åííûé â âåòâü ñ ðåçèñòîðîì R íà ðèñ. 3.10,

ïîêàçûâàåò i

= 3 À, âêëþ÷åííûé â öåïü ñ èíäóêòèâíîñòüþ $

= 3 À, à âêëþ÷åííûé ïîñëåäîâàòåëüíî ñ åìêîñòüþ $ i

= 7 À.

Êàêóþ âåëè÷èíó òîêà ïîêàæåò àìïåðìåòð, âêëþ÷åííûé íà âõîäå

ñõåìû?

Îòâåò: i = 5 À.

9. Âû÷èñëèòü âõîäíûå ñîïðîòèâëåíèÿ ñõåìû ðèñ. 3.10 íà ÷àñòîòå

f = 10 êÃö, åñëè R = 100 Îì, L = 1 ìÃí, Ñ = 1 ìêÔ.

Îòâåò Z = 4,4 $ j20,5 Îì.

10. ×åìó ðàâíû ìàêñèìàëüíîå è ìèíèìàëüíîå çíà÷åíèÿ êîýôôèöè-

åíòà ñâÿçè ìåæäó êàòóøêàìè?

11. Â êàêèõ åäèíèöàõ èçìåðÿåòñÿ âçàèìíàÿ èíäóêòèâíîñòü?

12. Ìîæåò ëè ñóììàðíàÿ èíäóêòèâíîñòü äâóõ èíäóêòèâíî ñâÿçàí-

íûõ êàòóøåê áûòü ðàâíîé 0?

13. Ê ñõåìå ðèñ. 3.19 ïðèëîæåíî íàïðÿæåíèå U = 10 Â. Ñîïðîòèâ-

ëåíèå ðåçèñòîðîâ R

= R

= 40 Îì. Èíäóêòèâíûå ñîïðîòèâëå-

íèÿ êàòóøåê X

= 100 Îì, X

= 50 Îì. Êîýôôèöèåíò ñâÿçè

ìåæäó íèìè K = 0,6. Îïðåäåëèòü ðàçíîñòü ïîòåíöèàëîâ ìåæäó

îäíîèìåííûìè çàæèìàìè ýòèõ êàòóøåê.

Îòâåò U = 4 + j4,88 Â.

14. Â ñõåìå íà ðèñóíêå 3.21 (á) ñîïðîòèâëåíèå ðåçèñòîðîâ R

= 20 Îì, R

= 0 Îì, ñîïðîòèâëåíèå èíäóêòèâíîñòåé X

= X

= 30 Îì, êîýôôèöèåíò ñâÿçè ìåæäó êàòóøêàìè Ê = 0,5.

Îïðåäåëèòü ýêâèâàëåíòíîå âõîäíîå ñîïðîòèâëåíèå öåïè.

Îòâåò: Z

âõ

= 4,76 + j7,56 Îì.

15. Êàêîâû îñîáåííîñòè ðàñ÷åòà öåïåé ñ èíäóêòèâíûìè ñâÿçÿìè?

16. Êàêîå óñòðîéñòâî íàçûâàåòñÿ òðàíñôîðìàòîðîì? Êàêèå âèäû

òðàíñôîðìàòîðîâ èçâåñòíû?

17. Ñîñòàâèòü óðàâíåíèÿ áàëàíñà ìîùíîñòè äëÿ ñõåìû, èçîáðàæåí-

íîé íà ðèñ. 3.15.

18. Â ñõåìå, èçîáðàæåííîé íà ðèñ. 3.7, U = 10 Â, u

= 5 Â, u

= 11 Â, ñîïðîòèâëåíèå ðåçèñòîðà R = 40 Îì. Îïðåäåëèòü êîì-

ïëåêñíóþ ìîùíîñòü, ïîòðåáëåííóþ öåïüþ.

Îòâåò: S

ïîòð

= 1,6 $ j1,2.

19. Êàêèì îáðàçîì ìîæíî óìåíüøèòü ðåàêòèâíóþ ñîñòàâëÿþùóþ

ìîùíîñòè ïîòðåáëÿåìóþ ïðåäïðèÿòèåì èç ñåòè?

20. Êàêîâû ñõåìû èíòåãðèðóþùèõ è äèôôåðåíöèðóþùèõ öåïåé íà

îïåðàöèîííîì óñèëèòåëå?

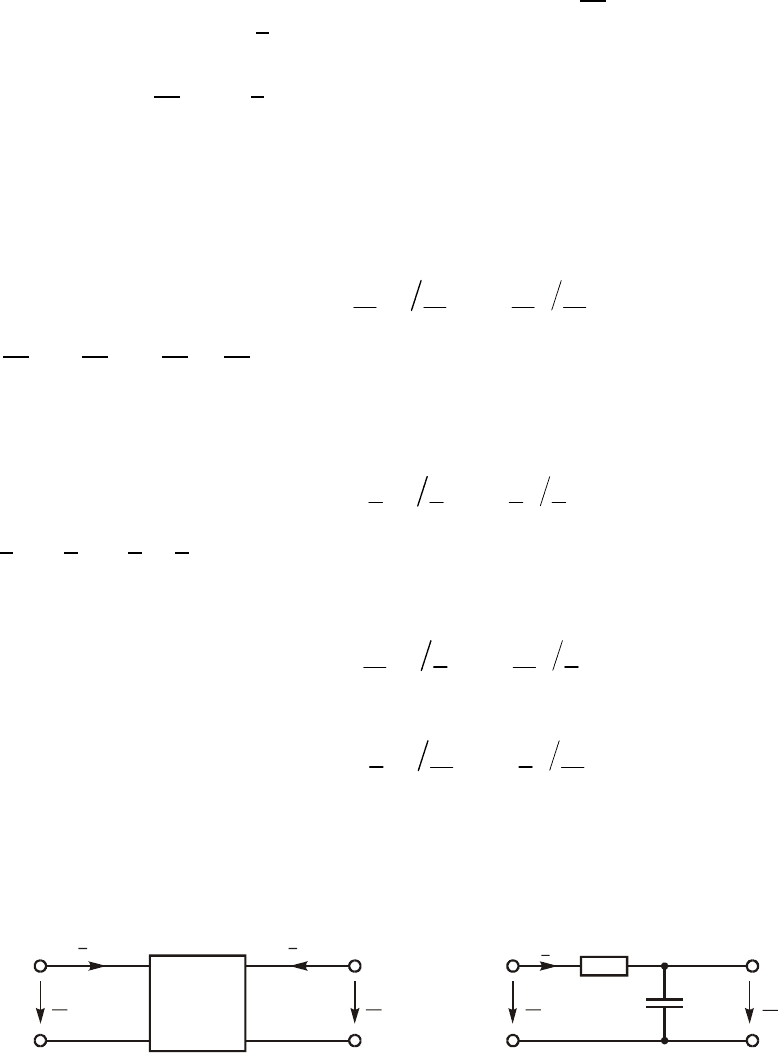
110

()

Ðèñ. 4.1

Ðèñ. 4.2

ÃËÀÂÀ 4. ×ÀÑÒÎÒÍÛÅ ÕÀÐÀÊÒÅÐÈÑÒÈÊÈ

ÝËÅÊÒÐÈ×ÅÑÊÎÉ ÖÅÏÈ

4.1. Êîìïëåêñíûå ïåðåäàòî÷íûå ôóíêöèè ëèíåéíûõ

ýëåêòðè÷åñêèõ öåïåé

Âàæíåéøåé õàðàêòåðèñòèêîé ëèíåéíîé ýëåêòðè÷åñêîé öåïè ÿâ-

ëÿåòñÿ êîìïëåêñíàÿ ïåðåäàòî÷íàÿ ôóíêöèÿ H(jw). Ïðè ýòîì

ýëåêòðè÷åñêóþ öåïü óäîáíî èçîáðàæàòü â âèäå ÷åòûðåõïîëþñíèêà

(ðèñ. 4.1), íà âõîäíûå çàæèìû (1 $ 1¢) êîòîðîãî ïîäàåòñÿ ñèãíàë â

âèäå íàïðÿæåíèÿ ñ êîìïëåêñíîé àìïëèòóäîé U

, èëè òîêà ñ êîì-

ïëåêñíîé àìïëèòóäîé I

, à ðåàêöèÿ ñíèìàåòñÿ ñ âûõîäíûõ çàæè-

ìîâ (2 $ 2¢) òàêæå â âèäå íàïðÿæåíèÿ èëè òîêà ñ êîìïëåêñíûìè

àìïëèòóäàìè U

, I

. Êîìïëåêñíàÿ ïåðåäàòî÷íàÿ ôóíêöèÿ

(ÊÏÔ) îïðåäåëÿåòñÿ êàê îòíîøåíèå êîìïëåêñíîé àìïëèòóäû ðå-

àêöèè öåïè ê êîìïëåêñíîé àìïëèòóäå âõîäíîãî âîçäåéñòâèÿ.

Â çàâèñèìîñòè îò òèïîâ âõîäíîãî âîçäåéñòâèÿ è ðåàêöèè öåïè

ðàçëè÷àþò ñëåäóþùèå âèäû ÊÏÔ:

1. Êîìïëåêñíàÿ ïåðåäàòî÷íàÿ ôóíêöèÿ ïî íàïðÿæåíèþ

(

)

2121

HUUUU

, (4.1)

ãäå U

, U

$ êîìïëåêñíûå àìïëèòóäû è êîìïëåêñíûå

äåéñòâóþùèå çíà÷åíèÿ íàïðÿæåíèÿ âîçäåéñòâèÿ íà âõîäå è íàïðÿ-

æåíèÿ ðåàêöèè íà âûõîäå.

2. Êîìïëåêñíàÿ ïåðåäàòî÷íàÿ ôóíêöèÿ ïî òîêó

(

)

2121

HIIII

, (4.2)

ãäå I

, I

% êîìïëåêñíûå àìïëèòóäû è äåéñòâóþùèå çíà-

÷åíèÿ òîêà âîçäåéñòâèÿ è òîêà ðåàêöèè.

3. Êîìïëåêñíîå ïåðåäàòî÷íîå ñîïðîòèâëåíèå

(

)

HUIUI

. (4.3)

4. Êîìïëåêñíàÿ ïåðåäàòî÷íàÿ ïðîâîäèìîñòü

(

)

HIUIU

(4.4)

Èç äàííûõ îïðåäåëåíèé ñëåäóåò, ÷òî H

(jw) è H

(jw) ÿâëÿþòñÿ

áåçðàçìåðíûìè âåëè÷èíàìè, a H

(jw) è H

(jw) $ èìåþò ñîîò-

âåòñòâåííî ðàçìåðíîñòè ñîïðîòèâëåíèÿ è ïðîâîäèìîñòè.