Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.

451
j
W
p
1
1
1
-1
-1
p
4
p
3
p
2
a
0,5-0,5
0,5
-0,5
à
)
j
W
p
1
1
-1
p
4
p
3
p
2
a
á
)
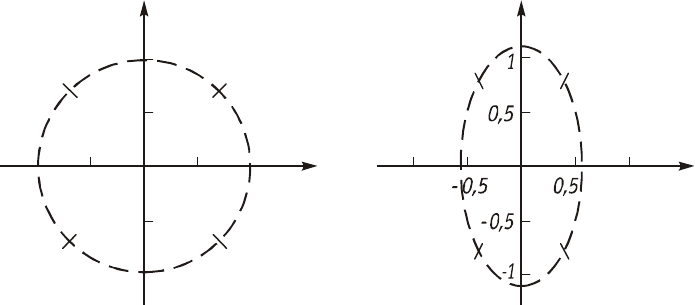
Ðèñ. 17.5
ãäå T
m
(W) $ ïîëèíîì ×åáûøåâà ñòåïåíè (ïîðÿäêà) m; e $ êîýôôè-
öèåíò íåðàâíîìåðíîñòè, îïðåäåëÿåìûé (17.6) èëè (17.7).
Ôèëüòðû ñ ÷àñòîòíûìè õàðàêòåðèñòèêàìè (17.15) íàçûâàþòñÿ
ôèëüòðàìè ×åáûøåâà. Ïðîàíàëèçèðóåì ÷àñòîòíûå õàðàêòåðèñòè-
êè ôèëüòðà ×åáûøåâà. Äëÿ ýòîãî âíà÷àëå ðàññìîòðèì ñâîéñòâà ïî-
ëèíîìîâ T
m
(W). Íèæå ïðèâåäåíû øåñòü ïåðâûõ ïîëèíîìîâ ×åáû-
øåâà:
(
)
( )
( )
0
1
2
2
1;
;
21;
T
T
T
W=
W=W
W=W-
( )
( )
( )
3
3
42
4
53
5
43;
881;
16205.
T
T
T
W=W-W
W=W-W+
W=W-W+W
(17.16 à)
Ëþáîé ïîëèíîì ×åáûøåâà ïðè m 2 ìîæåò áûòü âû÷èñëåí ïî
ðåêóððåíòíîé ôîðìóëå T
m
(W) = 2WT
m$1
(W) $ T
m$ 2
(W). Òàêèì îá-
ðàçîì, âûðàæåíèÿ (17.15) óäîâëåòâîðÿþò îáùèì âûðàæåíèÿì
(17.1) $ (17.3) õàðàêòåðèñòèê ïîëèíîìèàëüíûõ ôèëüòðîâ.
Ñóùåñòâóåò åäèíàÿ òðèãîíîìåòðè÷åñêàÿ ôîðìà çàïèñè ïîëèíî-
ìîâ ×åáûøåâà â èíòåðâàëå $1 W 1:
(
)
cosarccos
m
Tm
W=W
. (17.16)(17.16 á)
Äåéñòâèòåëüíî, T
0
(W) = cos0arccos W = 1; T
1
(W) = cos1arccosW =
= W; T
2
(W) = cos2arccos W = 2cos
2
arccosW $ 1 = 2W
2
$ 1. Âíå èí-
òåðâàëà $1 W 1 ïîëèíîìû T
m
(W) òàêæå ïðåäñòàâëÿþòñÿ â òðè-
ãîíîìåòðè÷åñêîé ôîðìå:
(
)
chArch
m
Tm
W=W
. (17.16 â)
Àíàëèç ïîâåäåíèÿ ïîëèíîìîâ ×åáûøåâà ïîêàçûâàåò, ÷òî â èíòåð-
âàëå $1 W 1 óãîë Q = arccosW èçìåíÿåòñÿ îò $p (ïðè W = $1)
äî 0 (ïðè W = 1), ïîýòîìó ïîëèíîì T
m
(W) = cosmQ ðîâíî m ðàç
ïðèíèìàåò çíà÷åíèÿ, ðàâíûå íóëþ, è m + 1 ðàç äîñòèãàåò çíà÷å-
íèé, ðàâíûõ +1 èëè $1 è ÷åðåäóþùèõñÿ äðóã ñ äðóãîì. Âíå èíòåð-
âàëà $1 W 1 ïîëèíîì T
m
(W) ñîãëàñíî ôîðìóëå (17.16 â) ìîíî-
452
À
ð
max
W
ç
W
À
ð
À
ð
m
i
n
0
á
)
-1
-1 1
1
T
4
()
W
1
à
)
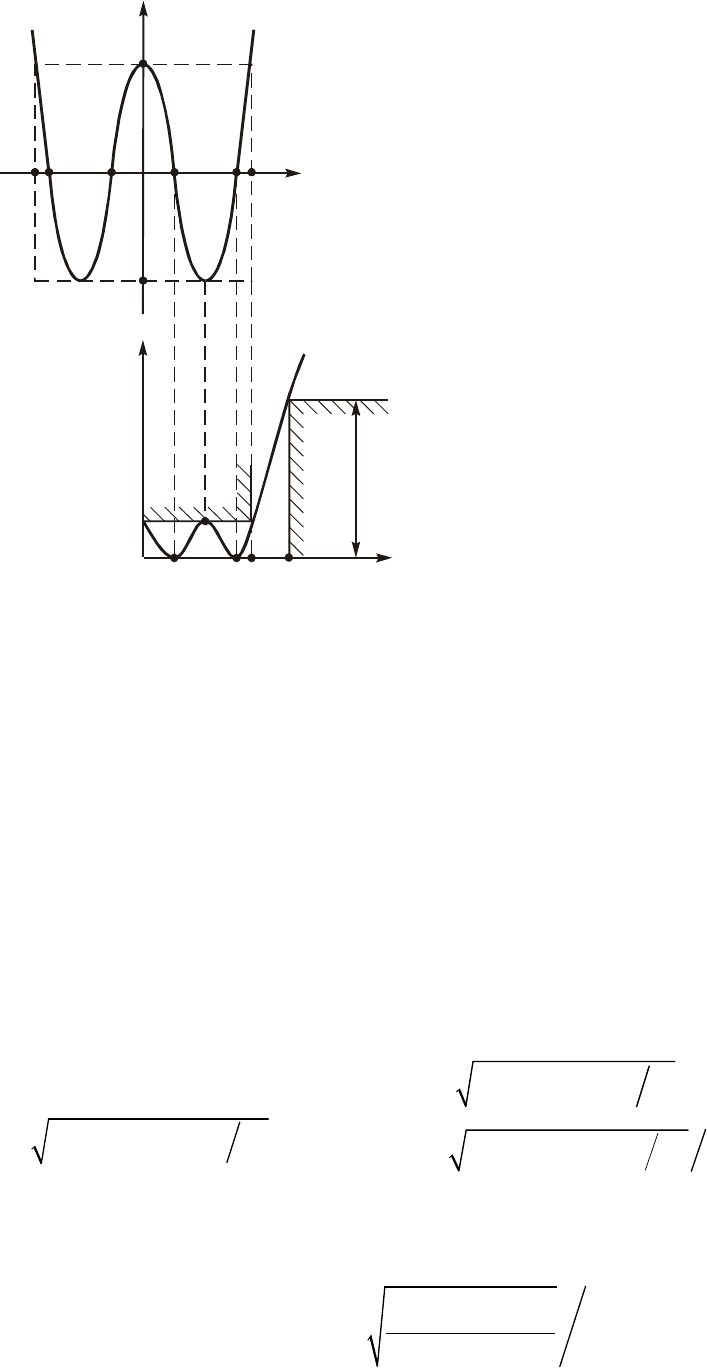
Ðèñ. 17.6
òîííî âîçðàñòàåò.  êà÷åñòâå
ïðèìåðà íà ðèñ. 17.6, à èçîáðàæåí
ãðàôèê ïîëèíîìà ×åáûøåâà
T
4
(W), ò. å. ïîëèíîìà ÷åòâåðòîãî
ïîðÿäêà.
 ñîîòâåòñòâèè ñ (17.15)
ðàáî÷åå îñëàáëåíèå A
p
(W) ôèëüòðà
×åáûøåâà íà òåõ ÷àñòîòàõ W, ãäå
ïîëèíîì T
m
(W) îáðàùàåòñÿ â íóëü,
òàêæå îáðàùàåòñÿ â íóëü. Íà
÷àñòîòàõ, íà êîòîðûõ T
m
(W) ðàâåí
±1, ðàáî÷åå îñëàáëåíèå äîñòèãàåò
âåëè÷èíû:
(
)
( )
p
2
p
0,1
p
10lg1
10lg1101.
max
A
max
A
A
=+e=
=+-=
Ñ ðîñòîì çíà÷åíèé ïîëèíîìà
T
m
(W) íà ÷àñòîòàõ W > 1 ðàáî÷åå
îñëàáëåíèå A
p
(W) òàêæå ìîíîòîí-
íî ðàñòåò. Íà ðèñ. 17.6, á ïðèâå-
äåí ãðàôèê ðàáî÷åãî îñëàáëåíèÿ
ôèëüòðà ×åáûøåâà ÷åòâåðòîãî ïîðÿäêà.
Ôèëüòðû ×åáûøåâà íàçûâàþò òàêæå ôèëüòðàìè ñ ðàâíîâîëíî-
âîé õàðàêòåðèñòèêîé îñëàáëåíèÿ â ïîëîñå ïðîïóñêàíèÿ.
Íà ðèñ. 17.7 ïîêàçàíû ÷àñòîòíûå çàâèñèìîñòè êâàäðàòà À×Õ
ôèëüòðà ×åáûøåâà äëÿ ðàçëè÷íûõ çíà÷åíèé m, ïîëó÷åííûå äëÿ
|Hð (jW)|
2
èç (17.15). Ïîäîáíûå çàâèñèìîñòè ìîãóò áûòü ïîñòðîåíû
äëÿ ðàáî÷åãî îñëàáëåíèÿ ôèëüòðà.
×òîáû õàðàêòåðèñòèêè ôèëüòðà îòâå÷àëè òðåáîâàíèÿì â ïîëîñå
íåïðîïóñêàíèÿ, íåîáõîäèìî âûáðàòü ïîðÿäîê ôèëüòðà m èç óñëîâèÿ
| Hð (jW)|
ç
2
W=
W
p
2
in
m
A
e
-
. Äëÿ ïîëîñû íåïðîïóñêàíèÿ T
m
(W) îïðå-
äåëÿåòñÿ ôîðìóëîé (17.16 â), ñëåäîâàòåëüíî, 1 + e
2
ñh
2
m´Arch W
ç
p
2
in
m
A
e
-
. Îòñþäà ñhmArch W
ç
(
)
p
2
2
1
min
A
e
-e
. Äàëåå m Arch W
ç
(
)
p
2
2
1
min
A
e
-
-e
è m
(
)
p
2
2
ç
ArchArch
1
min
A
e
-
eW
-
.
 ýòîé ôîðìóëå âåëè÷èíà A
p min
èçìåðÿåòñÿ â íåïåðàõ. Ïðè èñ-
ïîëüçîâàíèè åäèíèöû äåöèáåë ïîðÿäîê ôèëüòðà âû÷èñëÿåòñÿ èç
âûðàæåíèÿ:
m
p
0,1
ç
2
101
ArchArch
min
A
-
W
e
. (17.17 à)
Ñðàâíèâàÿ ÷àñòîòíûå õàðàêòåðèñòèêè ôèëüòðîâ Áàòòåðâîðòà è
×åáûøåâà, ñëåäóåò óêàçàòü, ÷òî ïîëèíîìû ×åáûøåâà ÿâëÿþòñÿ ïî-
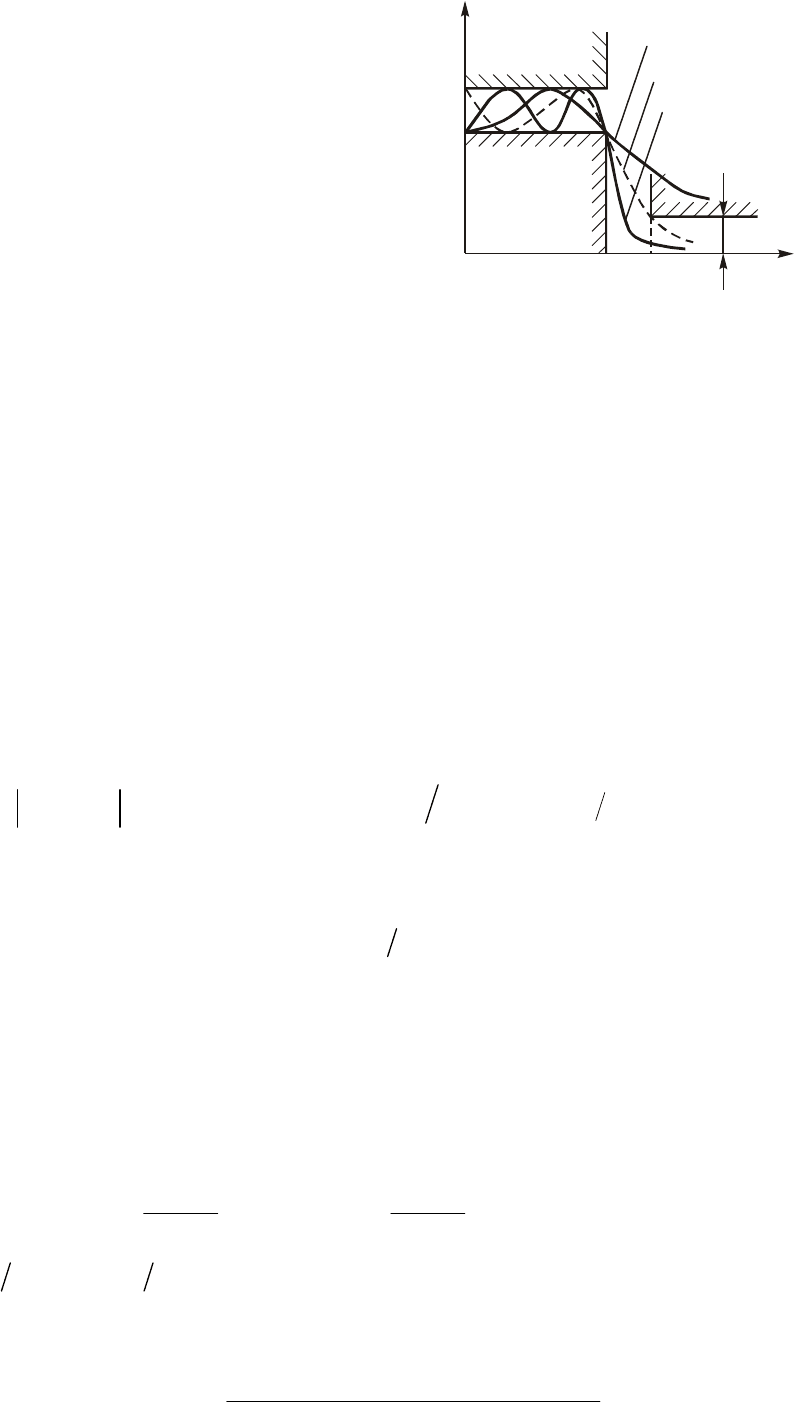
453
10
-
0,1
À
ð
max
10
-
0,1
À
ð
min
|H
ð
()|
W
2
W
ç
W
0
1
m
= 2
m
= 3
m
= 4
1
Ðèñ. 17.7
ëèíîìàìè íàèëó÷øåãî ïðèáëè-
æåíèÿ. Ýòî îçíà÷àåò, ÷òî ïðè
îäèíàêîâîì çíà÷åíèè m èç
âñåõ ïîëèíîìèàëüíûõ ôèëüò-
ðîâ, îñëàáëåíèÿ êîòîðûõ â ïî-
ëîñå ïðîïóñêàíèÿ íå ïðåâûøà-
þò A
p max
, íàèáîëüøèå çíà-
÷åíèÿ îñëàáëåíèÿ â ïîëîñå
íåïðîïóñêàíèÿ èìååò ôèëüòð
×åáûøåâà.  ÷àñòíîñòè, ðàáî-
÷åå îñëàáëåíèå ôèëüòðà ×åáû-
øåâà â ïîëîñå íåïðîïóñêàíèÿ ìîæåò ïðåâûøàòü (è âåñüìà çíà÷è-
òåëüíî) ðàáî÷åå îñëàáëåíèå ôèëüòðà Áàòòåðâîðòà ïðè ðàâíûõ çíà-
÷åíèÿõ m è A
p max
. Îäíàêî õàðàêòåðèñòèêà ðàáî÷åãî îñëàáëåíèÿ
ôèëüòðà Áàòòåðâîðòà èìååò â ïîëîñå ïðîïóñêàíèÿ ìîíîòîííûé õà-
ðàêòåð è ëåã÷å ïîääàåòñÿ êîððåêòèðîâàíèþ äëÿ óñòðàíåíèÿ èñêà-
æåíèé ïåðåäàâàåìûõ ñèãíàëîâ.
Âûáîð òèïà ïîëèíîìèàëüíûõ ôèëüòðîâ îïðåäåëÿåòñÿ êîíêðåò-
íûìè óñëîâèÿìè èõ ïðèìåíåíèÿ â àïïàðàòóðå ñâÿçè è ðàäèîòåõíè-
÷åñêèõ óñòðîéñòâàõ.
Äëÿ ïîëó÷åíèÿ ïåðåäàòî÷íîé ôóíêöèè ôèëüòðà ×åáûøåâà ïî-
ñòóïèì àíàëîãè÷íî òîìó, êàê äåëàëè ýòî äëÿ ôèëüòðîâ Áàòòåðâîð-
òà. Çàìåíèì îïåðàòîð jW íà îïåðàòîð ð è ïåðåéäåì îò ôóíêöèè
|Hð (jW)|
2
ê ôóíêöèè:
( ) ( ) ( ) ( )
2
22
ppp
11
m
HpHpHpTpj
éù
=-=+e
ëû
.
Ïðåäñòàâèì ïîëèíîì T
m
(W) â âèäå (17.16 á) è íàéäåì ïîëþñû
ôóíêöèè |Hð (p)|
2
, ðåøèâ óðàâíåíèå:
( )
22
cosarccos10
mpj
e+=
. (17.17)((17.17 á)
Ïîñêîëüêó ñîãëàñíî (17.16 à) êîýôôèöèåíò ïðè ñòàðøåì ÷ëåíå
ïîëèíîìà ×åáûøåâà T
m
(W) ðàâåí 2
m$1
, òî êîýôôèöèåíò ïðè ñòàð-
øåì ÷ëåíå ïîëèíîìà â ëåâîé ÷àñòè ïðèâåäåííîãî âûøå óðàâíåíèÿ
ðàâåí e
2
2
2(m$1)
.
Êîðíè óðàâíåíèÿ (17.17 á), êàê ìîæíî äîêàçàòü, îïðåäåëÿþòñÿ
àíàëèòè÷åñêè ñëåäóþùèì âûðàæåíèåì:
2121
shsinchcos,1,2,,2
22
k
kk
pjkm
mm
--
=gp+gp=K , (17.18)
ãäå
(
)
(
)
Arsh
11
m
g=
e
.
Èç êîðíåé â ëåâîé ïîëóïëîñêîñòè ñîñòàâëÿþòñÿ ñîìíîæèòåëè (p $
$ p
i
), è ïî òåîðåìå Âèåòà ñòðîèòñÿ ïåðåäàòî÷íàÿ ôóíêöèÿ ôèëüòðà:
( )
p
1
110
1
mm
m
HpH
pbpbpb
-
-
=
++++
K
,
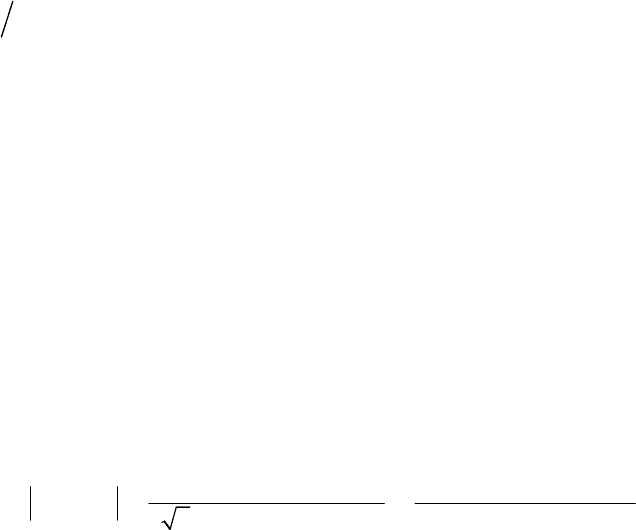
454
ãäå
(
)
1
12
m
H
-
=e× .
Ïðèìåð. Ïîñòðîèòü ïåðåäàòî÷íóþ ôóíêöèþ ôèëüòðà ×åáûøåâà âòîðîãî
ïîðÿäêà (m = 2), ðàáî÷åå îñëàáëåíèå â ïîëîñå ïðîïóñêàíèÿ (îò 0 äî 159 êÃö)
êîòîðîãî íå ïðåâûøàåò âåëè÷èíó A
p max
= 3 äÁ. Ãðàíè÷íàÿ ÷àñòîòà ïîëîñû
íåïðîïóñêàíèÿ 318 êÃö.
Êîýôôèöèåíò íåðàâíîìåðíîñòè e òàêîãî ôèëüòðà ñîãëàñíî (17.7) ðàâåí 1.
Ðàáî÷åå îñëàáëåíèå íà ÷àñòîòå W
ç
= 318/159 = 2 ñîñòàâëÿåò A
p
(W)
W =2
=
= 10lg(1 + ch
2
2Arch2) = 17 äÁ, ÷òî ïî÷òè íà 5 äÁ ïðåâûøàåò ðàáî÷åå îñëàá-
ëåíèå íà ýòîé æå ÷àñòîòå ôèëüòðà Áàòòåðâîðòà âòîðîãî ïîðÿäêà (ñì. ïðåäû-
äóùèé ïðèìåð).
Ðàñ÷åò ïîëþñîâ ôóíêöèè H
p
(p)H
p
($p) ïî ôîðìóëàì (17.18) äàåò âåëè÷è-
íû: p
1
= 0,322 + j0,777; p
2
= 0,322 $ j0,777; p
3
= $0,322 $ j0,777; p
4
=
= $0,322 + j0,777. Ðàñïîëîæåíèå ïîëþñîâ â êîìïëåêñíîé ïëîñêîñòè ïîêàçàíî
íà ðèñ. 17.5, á.
Ïåðåäàòî÷íàÿ ôóíêöèÿ ôèëüòðà:
( )
( )
( )
p
2
43
10,707
2
0,6450,707
Hp
pppp
pp
==
e--
++
.
 çàêëþ÷åíèå îòìåòèì, ÷òî äëÿ ïîëèíîìèàëüíûõ ôèëüòðîâ â
ñïðàâî÷íèêàõ ñîñòàâëåíû âåñüìà ïîëíûå òàáëèöû ïîëþñîâ è êî-
ýôôèöèåíòîâ ïåðåäàòî÷íûõ ôóíêöèé äëÿ ðàçëè÷íûõ âåëè÷èí
A
p max
è m. Ïîðÿäîê æå ôèëüòðîâ m îïðåäåëÿåòñÿ ïî ñïåöèàëüíûì
ãðàôèêàì, èñõîäÿ èç çàäàííûõ âåëè÷èí A
p max
, A
p min
è W
ç
.
Ôèëüòðû ñî âñïëåñêàìè îñëàáëåíèÿ (íà îñíîâå äðîáåé ×åáû-
øåâà è Çîëîòàðåâà). ×àñòîòíûå õàðàêòåðèñòèêè ïîëèíîìèàëüíûõ
ôèëüòðîâ, îïèñûâàåìûå âûðàæåíèÿìè (17.1)%(17.3), èìåþò ìîíî-
òîííûé õàðàêòåð â ïîëîñå íåïðîïóñêàíèÿ.  ÷àñòíîñòè, ðàáî÷åå îñ-
ëàáëåíèå òàêèõ ôèëüòðîâ ìîíîòîííî âîçðàñòàåò ïî ìåðå óäàëåíèÿ
îò ïîëîñû ïðîïóñêàíèÿ (ðèñ. 17.4, à è 17.6, á).
Ïðè «æåñòêèõ» òðåáîâàíèÿõ ê ÷àñòîòíûì õàðàêòåðèñòèêàì (ìà-
ëàÿ ïåðåõîäíàÿ îáëàñòü ìåæäó ïîëîñàìè ïðîïóñêàíèÿ è íåïðîïóñ-
êàíèÿ è áîëüøàÿ âåëè÷èíà ðàáî÷åãî îñëàáëåíèÿ â ïîëîñå íåïðî-
ïóñêàíèÿ) ïîðÿäîê ôèëüòðà m ìîæåò ïîëó÷èòüñÿ î÷åíü áîëüøèì
äàæå â ñëó÷àå ïðèìåíåíèÿ ïîëèíîìà ×åáûøåâà. Ýòî ïðèâåäåò ê
ñóùåñòâåííîìó óñëîæíåíèþ ôèëüòðà è ê èçëèøíåìó «ðàñõîäó»
ýëåìåíòîâ.
 òàêèõ ñëó÷àÿõ öåëåñîîáðàçíî ïðèìåíÿòü ôèëüòðû ñî âñïëå-
ñêàìè ðàáî÷åãî îñëàáëåíèÿ â ïîëîñå íåïðîïóñêàíèÿ (ðèñ. 17.8, à).
Íà ÷àñòîòàõ âñïëåñêà W
¥1
, W
¥2
è ò. ä. ðàáî÷åå îñëàáëåíèå ôèëüòðà
ñòðåìèòñÿ ê áåñêîíå÷íîñòè; çà ñ÷åò ýòîãî âîçðàñòàåò êðóòèçíà õà-
ðàêòåðèñòèêè îñëàáëåíèÿ â ïåðåõîäíîé îáëàñòè. Ñîîòâåòñòâåííî
À×Õ ôèëüòðà íà ÷àñòîòàõ W
¥1
, W
¥2
è ò. ä. áóäåò îáðàùàòüñÿ â íóëü
(ðèñ. 17.8, á).
Äëÿ âûïîëíåíèÿ óêàçàííûõ óñëîâèé â âûðàæåíèÿõ (17.2)%
(17.3) èñïîëüçóþò ðàöèîíàëüíûå äðîáè âèäà:

455
À
ð
max
W
¥
1
W
ç
W
10
-0,1
À
ð
max
À
ð
,
äÁ
10
-0,1
À
ð
min
|H
ð
()|
j
W
2
0
0
1
à
)
á
)
W
¥
2
1
W
¥
1
W
ç
W
W
¥
2
1
Ðèñ. 17.8
( )
(
)
(
)
(
)
222222
2
12
p
2222
011
n
mm
mm
Hj
dddd
¥¥¥
-
-
W-WW-WW-W
W=
W+W++W+
K
K
; (17.19)
( )
( )( )
( )
2222
011
p
222222
12
1
ln
2
mm
mm
n
dddd
A
-
-
¥¥¥
W+W++W+
W=
W-WW-WW-W
K
K
. (17.20)
Äåéñòâèòåëüíî, êîãäà W ïðèíèìàåò çíà÷åíèÿ W
¥1
, W
¥2
, ..., W
¥n
,
|Hð (jW)|
2
= 0 è Að (W) ® ¥.
Ïåðåäàòî÷íàÿ ôóíêöèÿ òàêèõ ôèëüòðîâ ÿâëÿåòñÿ äðîáíî-ðàöè-
îíàëüíîé:
( )
(
)
(
)
(
)
222222
12
p
1
110
n
mm
mm
ppp
Hp
bpbpbpb
¥¥¥
-
-
+W+W+W
=
++++
K
K
(17.21)
è êðîìå ïîëþñîâ p
1
, p
2
, ..., p
m
èìååò íóëè:
0110220
;;;
nn
pjpjpj
¥¥¥
=±W=±W=±W
K
.
Ôèëüòðû ñî âñïëåñêàìè ðàáî÷åãî îñëàáëåíèÿ íàçûâàþò åùå
ôèëüòðàìè ñ íóëÿìè ïåðåäà÷è.
Ñðåäè ôèëüòðîâ ñî âñïëåñêàìè îñëàáëåíèÿ íàèáîëåå øèðîêîå
ðàñïðîñòðàíåíèå ïîëó÷èëè ôèëüòðû, ïîñòðîåííûå íà îñíîâå äðîáåé
×åáûøåâà è Çîëîòàðåâà. ×òîáû ïîëó÷èòü ÷àñòîòíûå õàðàêòåðèñòè-
êè ôèëüòðà íà îñíîâå äðîáåé ×åáûøåâà, íóæíî â ôîðìóëàõ
(17.14) èëè (17.15) èñïîëüçîâàòü â êà÷åñòâå ôóíêöèè ôèëüòðàöèè
äðîáü ×åáûøåâà. Îáîçíà÷àÿ åå F
m
(W), ïîëó÷èì:
( )
( )
( ) ( )
( ) ( )
2
22
p
22
p
22
p
11;
1
ln1[
Íï],
2
10lg1[
äÁ].
m
m
m
Hj
A
A
ü
éù
W=+eFW
ëû
ï
ï
éù
ý
W=+eFW
ëû
ï
éù
ï
W=+eFW
ëû
þ
(17.22)

456
 êà÷åñòâå ïðèìåðà óêàæåì äðîáü ×åáûøåâà ïÿòîãî ïîðÿäêà,
äëÿ êîòîðîé ïîñòðîåíû ãðàôèêè Að (W) è | Hð (jW)|
2
íà ðèñ. 17.8, à
è á:
( )
( )( )
53
012
5
2222
12¥¥
aW+aW+aW
FW=
W-WW-W
,
ãäå a
0
, a
1
è a
2
$ êîýôôèöèåíòû, ñâÿçàííûå ñ ÷àñòîòàìè âñïëåñêà
W
¥1
è W
¥2
.
Î÷åâèäíî, ÷òî ïîäñòàíîâêà ýòîé äðîáè â (17.22) ïðèâåäåò ïîñëå
íåêîòîðûõ ïðåîáðàçîâàíèé ê âûðàæåíèÿì îáùåãî âèäà (17.19) è
(17.20).
 ïîëîñå ïðîïóñêàíèÿ äðîáü ×åáûøåâà âåäåò ñåáÿ òàê æå, êàê è
ïîëèíîì ×åáûøåâà, ò. å. ðàáî÷åå îñëàáëåíèå ôèëüòðà íîñèò ðàâíîâîë-
íîâûé õàðàêòåð. Íà ÷àñòîòàõ âñïëåñêà W
¥1
è W
¥2
äðîáü ×åáûøåâà îá-
ðàùàåòñÿ â áåñêîíå÷íîñòü, ÷òî ïðèâîäèò ê áåñêîíå÷íî áîëüøîìó ðà-
áî÷åìó îñëàáëåíèþ.
Ñëåäóåò îòìåòèòü, ÷òî äðîáü ×åáûøåâà ÿâëÿåòñÿ äðîáüþ íàè-
ëó÷øåãî ïðèáëèæåíèÿ. Ýòî îçíà÷àåò, ÷òî ôèëüòð íà îñíîâå äðîáè
×åáûøåâà íà ëþáîé ÷àñòîòå ïîëîñû íåïðîïóñêàíèÿ èìååò áîëüøåå
çíà÷åíèå ðàáî÷åãî îñëàáëåíèÿ ïî ñðàâíåíèþ ñ ôèëüòðàìè íà îñíîâå
äðóãèõ äðîáåé (è ïîëèíîìîâ, êàê ÷àñòíûõ ñëó÷àåâ äðîáåé) ïðè
ïðî÷èõ ðàâíûõ óñëîâèÿõ (ïðè îäèíàêîâûõ ïîðÿäêàõ m, ïðè òàêîì
æå êîëè÷åñòâå è ðàñïîëîæåíèè ÷àñòîò âñïëåñêà è òåõ æå âåëè÷èíàõ
A
p max
).
×àñòíûì ñëó÷àåì äðîáåé ×åáûøåâà ÿâëÿþòñÿ äðîáè Çîëîòàðåâà:
( )
(
)
(
)
2222
10
S
mVV
V
Ra
¥
éù
W=WW-WW-W
ëû
Õ
, (17.23)
ãäå
(
)
(
)
22
10
11
VV
V
a
¥
éù
=W-W-
ëû
Õ
,
(
)
1,2,,2
VmS
=-
K
, çíà÷åíèå S
ðàâíî 0 äëÿ ÷åòíûõ m è ðàâíî 1 äëÿ íå÷åòíûõ m; m $ ïîðÿäîê
äðîáè; W
0V
, W
¥V
$ íóëè è ïîëþñû äðîáè, ñâÿçàííûå ñîîòíîøåíèåì
W
¥V
= W
ç
/W
0V
.
Èñïîëüçóÿ â êà÷åñòâå ôóíêöèè ôèëüòðàöèè â (17.14) è (17.15)
äðîáè Çîëîòàðåâà, ïîëó÷èì:
( )
( )
( ) ( )
( ) ( )
2
22
p
22
p
22
p
11;
1
ln1[
Íï],
2
10lg1[
äÁ].
m
m
m
HjR
AR
AR
ü
éù
W=+eW
ëû
ï
ï
éù
ý
W=+eW
ëû
ï
éù
ï
W=+eW
ëû
þ
(17.24)
Èç ôîðìóë (17.23) è (17.24) ñëåäóåò, ÷òî íóëè ôóíêöèè Að (W)
ñîâïàäàþò ñ íóëÿìè äðîáè Çîëîòàðåâà, à âñïëåñêè ôóíêöèè
Að (W) $ ñ ïîëþñàìè ýòîé æå äðîáè. Íóëè è ïîëþñû äðîáè Çîëî-
òàðåâà ìîæíî ðàññ÷èòûâàòü, îäíàêî îáû÷íî èõ îïðåäåëÿþò ïî êà-

457
À
ð
max
W
¥
1
W
ç
W
À
ð
,
äÁ
0
W
¥
2
1
W
01
W
02
Ðèñ. 17.9
R
ã
U
ã
1
1
¢
2
2
¢
LC
R
í
+
Z
âõ1
()
p
Ðèñ. 17.10
òàëîãàì äëÿ îïåðàòîðíûõ ïå-
ðåäàòî÷íûõ ôóíêöèé ÔÍ×.
Íà ðèñ. 17.9 ïîêàçàí ãðàôèê
Að (W) äëÿ ôèëüòðà Çîëîòà-
ðåâà ïÿòîãî ïîðÿäêà.
Äðîáè Çîëîòàðåâà òàê æå,
êàê è ïîëèíîìû ×åáûøåâà,
äàþò ðàâíîâîëíîâóþ õàðàêòå-
ðèñòèêó ðàáî÷åãî îñëàáëåíèÿ
ôèëüòðà â ïîëîñå ïðîïóñêà-
íèÿ. Îäíàêî â ïîëîñå íåïðî-
ïóñêàíèÿ ó ôèëüòðîâ Çîëîòà-
ðåâà çíà÷åíèÿ âñåõ ìèíèìóìîâ ðàáî÷åãî îñëàáëåíèÿ îêàçûâàþòñÿ
îäèíàêîâûìè è ðàâíûìè çíà÷åíèþ ðàáî÷åãî îñëàáëåíèÿ íà ÷àñòîòå
W
ç
. Òàêèå ôèëüòðû íàçûâàþòñÿ òàêæå ôèëüòðàìè ñ èçîýêñòðå-
ìàëüíûìè õàðàêòåðèñòèêàìè ðàáî÷åãî îñëàáëåíèÿ.
Ôèëüòðû ñ õàðàêòåðèñòèêàìè Çîëîòàðåâà ìîæíî ðàññìàòðèâàòü
êàê ÷àñòíûé ñëó÷àé ôèëüòðîâ ñ õàðàêòåðèñòèêàìè ×åáûøåâà, êîãäà
çíà÷åíèÿ ìèíèìóìîâ îñëàáëåíèÿ ôèëüòðà â ïîëîñå íåïðîïóñêàíèÿ
âûðàâíåíû, à ÷èñëî âñïëåñêîâ $ ìàêñèìàëüíî âîçìîæíîå ïðè âû-
áðàííîì çíà÷åíèè m.
17.3. Ðåàëèçàöèÿ ôèëüòðîâ íèæíèõ ÷àñòîò
Ëåñòíè÷íûå ïîëèíîìèàëüíûå LC-ôèëüòðû. Ëþáûå èç ðàñ-
ñìîòðåííûõ âûøå ôèëüòðîâ, êàê ïîëèíîìèàëüíûå, òàê è ñî
âñïëåñêàìè îñëàáëåíèÿ ìîãóò áûòü ðåàëèçîâàíû â âèäå ïàññèâ-
íûõ LC-öåïåé.
Ïàññèâíûå LC-ôèëüòðû îáû÷íî ïðåäñòàâëÿþò ñîáîé ðåàêòèâ-
íûé ëåñòíè÷íûé ÷åòûðåõïîëþñíèê, âêëþ÷åííûé ìåæäó ãåíåðàòî-
ðîì ñ àêòèâíûì âíóòðåííèì ñîïðîòèâëåíèå R
ã
è íàãðóçêîé ñ àêòèâ-
íûì ñîïðîòèâëåíèåì R
í
(ðèñ. 17.10). Âõîäíîå ñîïðîòèâëåíèå ðåàê-
òèâíîãî ÷åòûðåõïîëþñíèêà, íàãðóæåííîãî íà ñîïðîòèâëåíèå R
í
,
îáîçíà÷åíî íà ðèñóíêå Z
âõ1
(ð).
Åñëè ôèëüòð ñî ñòîðîíû çàæèìîâ 1%1¢ ðàññìàòðèâàòü êàê
äâóõïîëþñíèê, îáðàçîâàííûé ðåàêòèâíûì ÷åòûðåõïîëþñíèêîì è
íàãðóçêîé R
í
, òî, çíàÿ âûðàæåíèå
Z
âõ1
(ð), ìîæíî ðåàëèçîâàòü äàííûé
äâóõïîëþñíèê îäíèì èç èçâåñòíûõ
â òåîðèè öåïåé ìåòîäîâ ñèíòåçà
äâóõïîëþñíèêîâ. Òàêèì îáðàçîì,
çàäà÷à ðåàëèçàöèè ôèëüòðà ñâîäèò-
ñÿ ê ðåàëèçàöèè äâóõïîëþñíèêà ïî
åãî çàäàííîìó âõîäíîìó ñîïðîòèâ-
ëåíèþ. Èäåÿ äàííîãî ïîäõîäà ïðè-

458
1,41 ìÃí
1,41 íÔ
1 ê
1 ê
+
U
ã
Z
âõ1
()
p
Ðèñ. 17.11
íàäëåæèò Ñ. Äàðëèíãòîíó è ìåòîä ðåàëèçàöèè ôèëüòðîâ íàçûâàåò-
ñÿ ìåòîäîì Äàðëèíãòîíà.
Íà âõîäå ôèëüòðà èìååò ìåñòî íåñîãëàñîâàííîñòü, êîòîðóþ ìîæíî
îöåíèòü, ââåäÿ â ðàññìîòðåíèå êîýôôèöèåíò îòðàæåíèÿ (16.25)
( )
(
)
( )
ãâõ1
ãâõ1
RZp
p
RZp
-
s=
+
. (17.25)
Ðåøàÿ (17.25) îòíîñèòåëüíî Z
âõ1
(ð), ïîëó÷àåì:
( )
(
)
( )
âõ1 ã
1
1
p
ZpR
p
-s
=
+s
. (17.26)
 (17.26) íåèçâåñòíûì ÿâëÿåòñÿ êîýôôèöèåíò îòðàæåíèÿ s(ð).
 ñâîþ î÷åðåäü, êîýôôèöèåíò îòðàæåíèÿ s(ð) ñâÿçàí ñ ïåðåäàòî÷-
íîé ôóíêöèåé H
p
(ð) = w(ð)/v(ð) ñîîòíîøåíèåì (16.26):
(
)
(
)
(
)
(
)
( ) ( ) ( ) ( )
( ) ( )
pp
1
.
ppHpHp
vpvpwpwp
vpvp
ss-=--=
---
=
-
(17.27)
Èç (17.27) ñëåäóåò, ÷òî çíàìåíàòåëü ó s(ð) òàêîé æå, êàê è ó
H
p
(ð): èì ÿâëÿåòñÿ ïîëèíîì v(ð). Îñòàåòñÿ íàéòè íóëè ïðàâîé ÷àñ-
òè âûðàæåíèÿ (17.7) è ïîëîâèíó èç íèõ «ïðèïèñàòü» ïîëèíîìó ÷èñ-
ëèòåëÿ s(ð). Ïîñëåäíèé ôîðìèðóåòñÿ èç íóëåé ïî òåîðåìå Âèåòà.
Ïðèìåð. Ðåàëèçîâàòü ôèëüòð íèæíèõ ÷àñòîò Áàòòåðâîðòà âòîðîãî ïîðÿäêà
èç ïðèìåðà (ñòð. 450) â âèäå ïàññèâíîé LC-ñõåìû. Âíóòðåííåå ñîïðîòèâëåíèå
ãåíåðàòîðà 1 êÎì.
 ïðèìåðå áûëà ïîëó÷åíà ïåðåäàòî÷íàÿ ôóíêöèÿ Áàòòåðâîðòà âòîðîãî ïî-
ðÿäêà H
p
(p) = 1/(p
2
+ 1,41p + 1) äëÿ íîðìèðîâàííûõ çíà÷åíèé ÷àñòîòû W =
= w/w
í
= w/(2p×159 ×10
3
) = w/10
6
, ãäå w
í
= w
ï
= 2p f
ï
. Ðåàëèçàöèÿ íîðìèðîâàí-
íîé ïåðåäàòî÷íîé ôóíêöèè ïðèâåäåò ê ñõåìå ñ íîðìèðîâàííûìè çíà÷åíèÿìè
ðåàêòèâíûõ ýëåìåíòîâ (îáîçíà÷èì èõ
,
LC
)
)
), êîòîðûå çàòåì íåîáõîäèìî äå-
íîðìèðîâàòü äëÿ ïîëó÷åíèÿ ðåàëüíûõ çíà÷åíèé.
 ñîîòâåòñòâèè ñ (17.27)
( ) ( )
( )( )
22
4
22
11
1
1,4111,411
.
1,4111,411
pp
pppp
p
pppp
ss-=-=
++-+
=
++-+
459
Íóëè ýòîé ôóíêöèè p
01, 02, 03, 04
= 0. Ïîëèíîì ÷èñëèòåëÿ s(ð) â ñîîòâåòñòâèè ñ
òåîðåìîé Âèåòà ðàâåí (p $ p
01
) × (p $ p
02
) = p
2
. Îòñþäà s(ð) = p
2
/(p
2
+ 1,41p +
+ 1).
Ñîãëàñíî (17.26)
( )
(
)
( )
22
33
3
âõ1
2
22
11,411
1,411010
10
21,411
11,411
ppp
p
Zp
pp
ppp
-++
×+
==
++
+++
.
Ðåàëèçàöèþ äâóõïîëþñíèêà ñî âõîäíûì ñîïðîòèâëåíèåì Z
âõ1
(p) îñóùåñòâèì
ðàçëîæåíèåì â öåïíóþ (ëåñòíè÷íóþ) äðîáü ïî ìåòîäó Êàóýðà. Ïðåäñòàâèì
Z
âõ1
(p) = 1/Y
âõ1
(p) è ïðîâåäåì ðàçëîæåíèå ïðîâîäèìîñòè:
33
2
3
2
1-é ýòàï
1,411010
21,411
1,4110
21,41
1
p
pp
p
pp
-
×+
++
-
×
+
33
3
3
3
-é ýòàï
2
1,411010
1
1,4110
1,4110
10
p
p
p
-
×+
-
×
×
3
3
3-é ýòàï
10
1
1
10
0
-
-
Ïðîöåññ ðàçëîæåíèÿ çàêîí÷åí. Âõîäíîå ñîïðîòèâëåíèå Z
âõ1
(p), ïðåäñòàâëåí-
íîå öåïíîé äðîáüþ, èìååò âèä:
( )
âõ1
3
33
í
11
11
1,4110
1
1,4110110
Zp
pCp
pLG
p
-
-
==
+×+
+
×+
)
)
.
Ñõåìà äâóõïîëþñíèêà, âõîäíîå ñîïðîòèâëåíèå êîòîðîãî ñîîòâåòñòâóåò
äàííîé öåïíîé (ëåñòíè÷íîé) äðîáè, ïðèâåäåíà íà ðèñ. 17.11. Íîðìèðîâàííûå
çíà÷åíèÿ ýëåìåíòîâ
C
)
= 1,41 ×10
$3
,
L
)
= 1,41 ×10
3
. Àêòèâíàÿ ïðîâîäèìîñòü íà-
ãðóçêè íå íîðìèðóåòñÿ è ðàâíà G
í
= 10
$3
Ñì, ò. å. ñîïðîòèâëåíèå íàãðóçêè
R
í
= 1 êÎì. Äåíîðìèðîâàòü çíà÷åíèÿ ýëåìåíòîâ ìîæíî ñëåäóþùèì îáðàçîì.
Êîìïëåêñíàÿ ïðîâîäèìîñòü íîðìèðîâàííîé åìêîñòè
(
)
í
jjjC
CC
=ww=W
W
))
,
îòêóäà íåíîðìèðîâàííîå çíà÷åíèå åìêîñòè
í
C
C
=w
)
= 1,41 ×10
$3
/10
6
=
= 1,41 ×10
$9
Ô = 1,41 íÔ.
Ïîäîáíûì îáðàçîì êîìïëåêñíîå ñîïðîòèâëåíèå íîðìèðîâàííîé èíäóêòèâ-
íîñòè
(
)
í
jjjL
LL
=ww=W
W
))
èëè
í
L
L
=w
)
= 1,41 ×10
3
/10
6
= 1,41 ×10
$3
Ãí =
= 1,41 ìÃí.
Àíàëîãè÷íî ðàññìîòðåííîìó ïðèìåðó ðåøàåòñÿ çàäà÷à ðåàëèçà-
öèè ôèëüòðà ëþáîãî ïîðÿäêà. Íàïðèìåð, ïîëèíîìèàëüíûé ÔÍ×
ïÿòîãî ïîðÿäêà (m = 5) ðåàëèçóåòñÿ â âèäå îäíîé èç äâóõ ñõåì,
ïîêàçàííûõ íà ðèñ. 17.12, à è á. Êîëè÷åñòâî ðåàêòèâíûõ ýëåìåíòîâ
îïðåäåëÿåòñÿ ïîðÿäêîì ôèëüòðà m. Îòëè÷èå ôèëüòðà Áàòòåðâîðòà
îò ôèëüòðà ×åáûøåâà áóäåò çàêëþ÷àòüñÿ â ýòîì ñëó÷àå òîëüêî â
ðàçíûõ çíà÷åíèÿõ ðåàêòèâíûõ ýëåìåíòîâ, ïîëó÷àåìûõ â ïðîöåññå
ðåàëèçàöèè ñîîòâåòñòâóþùèõ ïåðåäàòî÷íûõ ôóíêöèé.

460
à
)
L
2
L
4
C
1
C
3
C
5
á
)
L
1
L
3
C
2
C
4
L
5
Ðèñ. 17.12
à
)
L
2
C
1
C
4
C
7
á
)
L
1
L
4
C
2
C
5
L
7
W
¥
1
W
¥
1
W
¥
2
L
3
L
6
C
3
L
5
W
¥
2
C
6
Ðèñ. 17.13
Ëåñòíè÷íûå ôèëüòðû ñî âñïëåñêàìè îñëàáëåíèÿ. Ïî ïîäîáíîé
ñõåìå îñóùåñòâëÿåòñÿ è ðåàëèçàöèÿ ïåðåäàòî÷íûõ ôóíêöèé ôèëüò-
ðîâ ñî âñïëåñêàìè îñëàáëåíèÿ (×åáûøåâà èëè Çîëîòàðåâà). Ðàçëî-
æåíèå âõîäíîãî ñîïðîòèâëåíèÿ òàêèõ ôèëüòðîâ â öåïíóþ äðîáü
ïðèâåäåò ê ñõåìàì, ñîäåðæàùèì ðåçîíàíñíûå êîíòóðû, â êîòîðûõ
ðåçîíàíñû ïðîèñõîäÿò íà ÷àñòîòàõ W
¥1
, W
¥2
, ... Íàëè÷èå ýòèõ êîí-
òóðîâ è îáåñïå÷èâàåò áåñêîíå÷íî áîëüøîå çàòóõàíèå íà ÷àñòîòàõ
âñïëåñêà.
Òàê, ÔÍ× ïÿòîãî ïîðÿäêà ñî âñïëåñêàìè îñëàáëåíèÿ íà ÷àñòî-
òàõ W
¥1
è W
¥2
ðåàëèçóåòñÿ â âèäå îäíîé èç ñõåì, ïðèâåäåííûõ íà
ðèñ. 17.13, à è á. È â ïåðâîé è âî âòîðîé ñõåìàõ êîíòóðû ðàññ÷è-
òàíû íà ðåçîíàíñíûå ÷àñòîòû W
¥1
è W
¥2
. Â ïåðâîé ñõåìå â ïàðàë-
ëåëüíûõ êîíòóðàõ ïðîèñõîäÿò ðåçîíàíñû òîêîâ; ñîïðîòèâëåíèÿ
êîíòóðîâ ïðèíèìàþò áåñêîíå÷íî áîëüøèå çíà÷åíèÿ.  ðåçóëüòàòå
íà ÷àñòîòàõ ðåçîíàíñîâ W
¥1
è W
¥2
íàáëþäàåòñÿ «îáðûâ» ïðîäîëü-
íûõ âåòâåé ôèëüòðà è ñèãíàë îò ãåíåðàòîðà â íàãðóçêó íå ïîñòóïà-
åò, ò. å. ôèëüòð âíîñèò áåñêîíå÷íî áîëüøîå îñëàáëåíèå. Âî âòîðîé
ñõåìå â ïîñëåäîâàòåëüíûõ êîíòóðàõ ïðîèñõîäÿò ðåçîíàíñû íàïðÿ-
æåíèé; ñîïðîòèâëåíèÿ êîíòóðîâ îáðàùàþòñÿ â íóëü. Òàêèì îáðà-
çîì, çäåñü íà ÷àñòîòàõ W
¥1
è W
¥2
ïîïåðå÷íûå âåòâè «çàêîðà÷èâàþò»
íàãðóçêó è ñèãíàë íà âûõîä ôèëüòðà íå ïîñòóïàåò. Òàêèì îáðàçîì,
èìååò ìåñòî áåñêîíå÷íî áîëüøîå îñëàáëåíèå.
Ðåàëèçàöèÿ ëåñòíè÷íûõ ôèëüòðîâ ïî êàòàëîãàì. Èç èçëîæåí-
íîãî ñëåäóåò, ÷òî ñèíòåç ôèëüòðîâ ïðåäñòàâëÿåò ñîáîé ñëîæíóþ
ïðîöåäóðó, ïîýòîìó ðàçðàáîò÷èêè ôèëüòðîâ ïûòàëèñü îáëåã÷èòü åå.
 ðåçóëüòàòå áûëè ñîçäàíû îáøèðíûå êàòàëîãè ôèëüòðîâ, ïðèìå-
íåíèå êîòîðûõ çíà÷èòåëüíî îáëåã÷àåò ïðîöåäóðó ñèíòåçà ÔÍ×.
Òàáë. 17.1 ïðåäñòàâëÿåò ñîáîé ñòðàíèöó èç òàêîãî êàòàëîãà, ãäå
