Бакалов В.П. Основы теории цепей. 3-е издание

Подождите немного. Документ загружается.

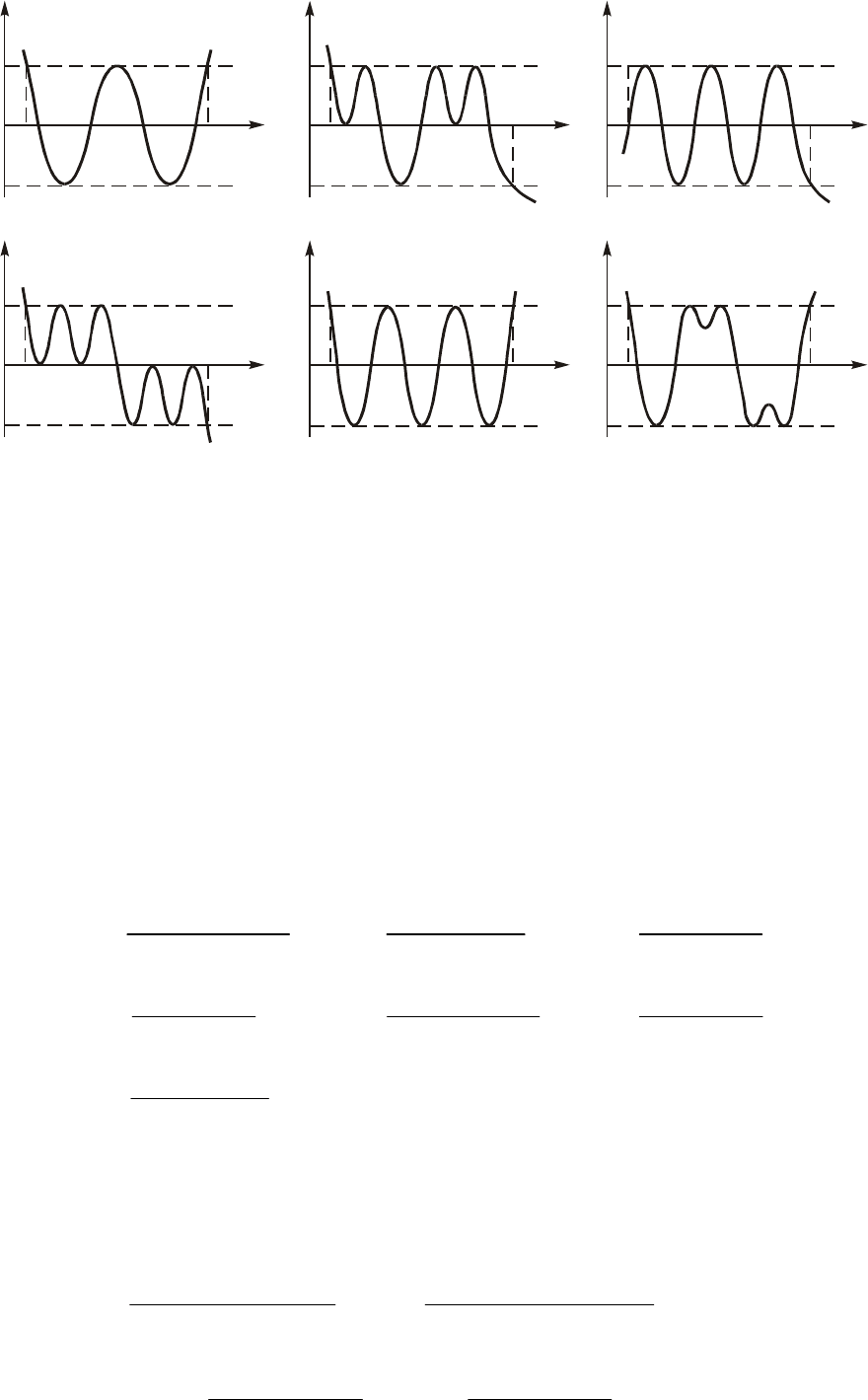
441

()()

xFx

)

()()

xFx

)

()()

xFx

)

()()

xFx

)

()()

xFx

)

()()

xFx

)

Ðèñ. 16.16

F(x) = x

+ a

x + a

. Îöåíèòü òî÷íîñòü àïïðîêñèìàöèè äëÿ ðàç-

ëè÷íûõ óçëîâ èíòåðïîëÿöèè.

5. Êàêîé èç âàðèàíòîâ àïïðîêñèìàöèè (ðèñ. 16.16, à%å) çàäàííîé

íà èíòåðâàëå (x

, x

) ôóíêöèè x(x) ïîëèíîìîì ïÿòîé ñòåïåíè

F(x) ñîîòâåòñòâóåò íàèëó÷øåìó ïðèáëèæåíèþ ïî êðèòåðèþ ×å-

áûøåâà?

Îòâåò: ä).

6. Êàêèå èç ïåðå÷èñëåííûõ ôóíêöèé óäîâëåòâîðÿþò óñëîâèÿì ôè-

çè÷åñêîé ðåàëèçóåìîñòè îïåðàòîðíûõ ïåðåäàòî÷íûõ ôóíêöèé è

ïî÷åìó:

222

1),2),3),

0,51311

551

4),5),6),

1511

7).

pppppp

jpppp

pppjppp

++++-+

++++++

Îòâåò: 1), 2), 6) è 7).

7. Ïî çàäàííûì êâàäðàòàì ìîäóëÿ ïåðåäàòî÷íûõ ôóíêöèé öåïåé

íàéòè èõ îïåðàòîðíûå ïåðåäàòî÷íûå ôóíêöèè:

4242

540,554,5

1),2).

251442064

w+w+w+w+

Îòâåò:

3243

1),2).

71268

pppp

++++

442

8. Íàéòè ñõåìó è âåëè÷èíû ýëåìåíòîâ ìîñòîâîãî ÷åòûðåõïîëþñíè-

êà ïîñòîÿííîãî õàðàêòåðèñòè÷åñêîãî ñîïðîòèâëåíèÿ, ðåàëèçóþ-

ùåãî ïåðåäàòî÷íóþ ôóíêöèþ (ïðè R = 1)

( )

Îòâåò:

1/2

9. Â ðåçóëüòàòå ñèíòåçà öåïè ïîëó÷åíû íîðìèðîâàííûå çíà÷åíèÿ

ýëåìåíòîâ

)

= 0,25,

)

= 0,75,

)

= 1,

)

= 0,5,

)

= 2,

)

= 0,5. Îïðåäåëèòü èñòèííûå ïàðàìåòðû ýëåìåíòîâ, åñëè ñîïðî-

òèâëåíèå íîðìèðîâàíèÿ R

= 10

Îì, à ÷àñòîòà íîðìèðîâàíèÿ

= 10

Îòâåò: R

= 250 Îì, R

= 750 Îì, L

= 1 ìÃí,

= 0,5 ìÃí, Ñ

= 2×10

Ô, Ñ

= 0,5×10

Ô.

10. Îïåðàòîðíàÿ ïåðåäàòî÷íàÿ ôóíêöèÿ öåïè èìååò âèä:

( )

342812

21021010

ppp

+×+×+

Âûïîëíèòü íîðìèðîâàíèå äàííîé ôóíêöèè, åñëè ÷àñòîòà íîð-

ìèðîâàíèÿ w

= 10

Îòâåò:

( )

221

ppp

+++

)

)))

11. ×òî òàêîå ïîëîæèòåëüíî-âåùåñòâåííûå ôóíêöèè (ÏÂÔ)?

12. Êàêèå èç ïðèâåäåííûõ äðîáíî-ðàöèîíàëüíûõ ôóíêöèé ÿâëÿþò-

ñÿ ÏÔÂ:

222

1),2),3).

pppp

+++

++++

Îòâåò: 2) è 3).

13. Êàêèìè ñâîéñòâàìè îáëàäàþò âõîäíûå ôóíêöèè ðåàêòèâíûõ

äâóõïîëþñíèêîâ?

14. Îïèøèòå ïðîöåäóðû ñèíòåçà ðåàêòèâíûõ äâóõïîëþñíèêîâ ïî

ìåòîäàì Ôîñòåðà è Êàóýðà.

443

)

ç1

ï1

ï2

ç2

ï1

ç1

ç2

ï2

Ðèñ. 17.1

ÃËÀÂÀ 17. ÔÈËÜÒÐÓÞÙÈÅ ÖÅÏÈ È ÈÕ ÑÈÍÒÅÇ

17.1. Êëàññèôèêàöèÿ ôèëüòðîâ

Ýëåêòðè÷åñêèé ôèëüòð $ ýòî óñòðîéñòâî, êîòîðîå ïðàêòè÷åñêè

íå îñëàáëÿåò ñïåêòðàëüíûå ñîñòàâëÿþùèå ñèãíàëà â çàäàííîé ïîëî-

ñå ÷àñòîò è çíà÷èòåëüíî îñëàáëÿåò (ïîäàâëÿåò) âñå ñïåêòðàëüíûå

ñîñòàâëÿþùèå âíå ýòîé ïîëîñû.

Ïîëîñà ÷àñòîò, â êîòîðîé îñëàáëåíèå ìàëî, íàçûâàåòñÿ ïîëîñîé

ïðîïóñêàíèÿ. Ïîëîñà ÷àñòîò, â êîòîðîé îñëàáëåíèå âåëèêî, íàçû-

âàåòñÿ ïîëîñîé íåïðîïóñêàíèÿ (çàäåðæèâàíèÿ). Ìåæäó ýòèìè ïî-

ëîñàìè íàõîäèòñÿ ïåðåõîäíàÿ îáëàñòü.

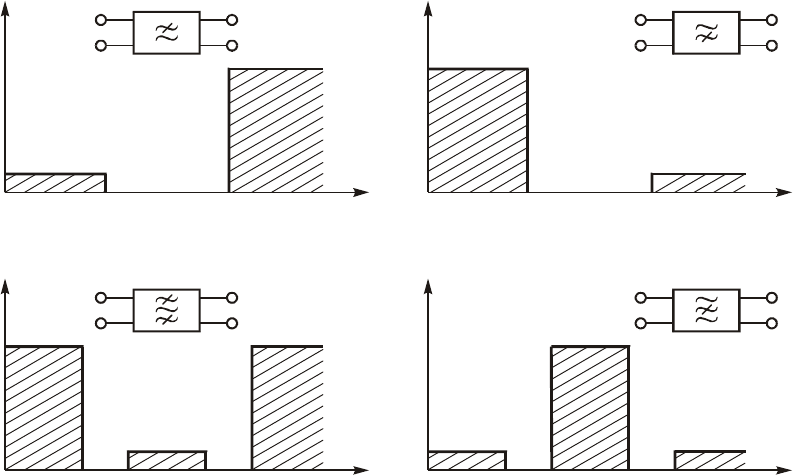
Ïî ðàñïîëîæåíèþ ïîëîñû ïðîïóñêàíèÿ íà øêàëå ÷àñòîò ðàçëè-

÷àþò ñëåäóþùèå ôèëüòðû:

íèæíèõ ÷àñòîò (ÔÍ×), â êîòîðûõ ïîëîñà ïðîïóñêàíèÿ ðàñïîëà-

ãàåòñÿ íà øêàëå ÷àñòîò îò w = 0 äî íåêîòîðîé ãðàíè÷íîé ÷àñòîòû

w=w

, à ïîëîñà íåïðîïóñêàíèÿ (çàäåðæèâàíèÿ) $ îò ÷àñòîòû

w=w

äî áåñêîíå÷íî áîëüøèõ ÷àñòîò (ðèñ. 17.1, à);

âåðõíèõ ÷àñòîò (ÔÂ×) ñ ïîëîñîé ïðîïóñêàíèÿ îò ÷àñòîòû

w=w

äî áåñêîíå÷íî áîëüøèõ ÷àñòîò è ïîëîñîé íåïðîïóñêàíèÿ îò

÷àñòîòû w = 0 äî

w=w

(ðèñ. 17.1, á);

ïîëîñîâûå (ÏÔ), â êîòîðûõ ïîëîñà ïðîïóñêàíèÿ

ï1ï2

ðàñ-

ïîëàãàåòñÿ ìåæäó ïîëîñàìè íåïðîïóñêàíèÿ

ç1

ç2

w¥

(ðèñ. 17.1, â);

çàãðàæäàþùèå (ðåæåêòîðíûå) (ÇÔ èëè ÐÔ), â êîòîðûõ ìåæäó

ïîëîñàìè ïðîïóñêàíèÿ

ï1

ï2

w¥

íàõîäèòñÿ ïîëîñà íåïðî-

444

)

()|

Ðèñ. 17.2

ïóñêàíèÿ

ç1ç2

(ðèñ. 17.1, ã);

ìíîãîïîëîñíûå, èìåþùèå íåñêîëüêî ïîëîñ ïðîïóñêàíèÿ.

Íà ðèñ. 17.1, à%ã ïîêàçàíû òàêæå óñëîâíûå îáîçíà÷åíèÿ

ôèëüòðîâ êàæäîãî òèïà â ñîîòâåòñòâèè ñ ÃÎÑÒ.

Â ñîîòâåòñòâèè ñ èñïîëüçóåìîé ýëåìåíòíîé áàçîé ê íàñòîÿùåìó

ìîìåíòó âûäåëèëèñü íåñêîëüêî êëàññîâ ôèëüòðîâ. Èñòîðè÷åñêè

ïåðâûìè (è âñå åùå øèðîêî ïðèìåíÿåìûìè) ÿâëÿþòñÿ ïàññèâíûå

ôèëüòðû, ñîäåðæàùèå ýëåìåíòû L è Ñ. Îíè íîñÿò íàçâàíèå LC-

ôèëüòðîâ.

Âî ìíîãèõ ñëó÷àÿõ íà ïðàêòèêå òðåáîâàëàñü êðàéíå âûñîêàÿ èç-

áèðàòåëüíîñòü (ðàçëè÷èå îñëàáëåíèé â ïîëîñàõ ïðîïóñêàíèÿ è íå-

ïðîïóñêàíèÿ â äåñÿòêè òûñÿ÷ ðàç). Ýòî ïðèâåëî ê ïîÿâëåíèþ

ôèëüòðîâ ñ ìåõàíè÷åñêèìè ðåçîíàòîðàìè: êâàðöåâûõ, ìàãíèòîñò-

ðèêöèîííûõ, ýëåêòðîìåõàíè÷åñêèõ.

Ïî-âèäèìîìó, ñàìûå çíà÷èòåëüíûå äîñòèæåíèÿ â îáëàñòè òåî-

ðèè è ïðîåêòèðîâàíèÿ ôèëüòðîâ ñâÿçàíû ñ óñïåõàìè ìèêðîýëåê-

òðîíèêè. Òðåáîâàíèÿ ìèêðîìèíèàòþðèçàöèè ðàäèîýëåêòðîííîé

àïïàðàòóðû çàñòàâèëè îòêàçàòüñÿ îò èñïîëüçîâàíèÿ èíäóêòèâíî-

ñòåé, êîòîðûå èìåþò áîëüøèå ãàáàðèòíûå ðàçìåðû, îñîáåííî íà

íèçêèõ ÷àñòîòàõ, è íå ïîääàþòñÿ èñïîëíåíèþ â ìèêðîìèíèàòþð-

íîì âèäå. Ïîÿâèëèñü àêòèâíûå RC-ôèëüòðû, ñîñòîÿùèå èç ðåçè-

ñòîðîâ, êîíäåíñàòîðîâ è àêòèâíûõ ïðèáîðîâ (íàïðèìåð, òðàíçè-

ñòîðîâ). Ýòè ôèëüòðû ìîãóò áûòü âûïîëíåíû â âèäå ìèêðîìî-

äóëüíîé êîíñòðóêöèè èëè èíòåãðàëüíîé ñõåìû. Ïðèìåíåíèå àê-

òèâíûõ RC-ôèëüòðîâ îãðàíè÷èâàåòñÿ ïîêà ñðàâíèòåëüíî íåáîëü-

øèì äèàïàçîíîì ÷àñòîò äî äåñÿòêîâ (èíîãäà ñîòåí) êèëîãåðö.

Ðàçðàáîòêà öèôðîâûõ ñèñòåì ñâÿçè è äîñòèæåíèÿ â îáëàñòè

öèôðîâûõ âû÷èñëèòåëüíûõ ìàøèí ñòèìóëèðîâàëè ñîçäàíèå

ôèëüòðîâ íà áàçå ýëåìåíòîâ öèôðîâîé è âû÷èñëèòåëüíîé òåõ-

íèêè $ öèôðîâûõ ôèëüòðîâ. Â ñèëó ñïåöèôèêè ýëåìåíòíîé áà-

çû öèôðîâûõ ôèëüòðîâ íå áóäåì äàëåå óïîìèíàòü î íèõ, õîòÿ

ðàñ÷åò òàêèõ ôèëüòðîâ ïðîèçâîäèòñÿ ìåòîäàìè òåîðèè ýëåêòðè-

÷åñêèõ öåïåé. Çàèíòåðåñîâàííûå ÷èòàòåëè ìîãóò îáðàòèòüñÿ ê

ñïåöèàëüíîé ëèòåðàòóðå ïî öèôðîâûì ôèëüòðàì.

Â èäåàëüíîì ñëó÷àå (èäåàëüíûé ôèëüòð) õàðàêòåðèñòèêà ðàáî-

÷åãî îñëàáëåíèÿ, íàïðèìåð äëÿ ÔÍ×, èìååò âèä, ïîêàçàííûé íà

ðèñ. 17.2, à. Ñ ðàáî÷èì îñëàáëåíèåì ñâÿçàíà ðàáî÷àÿ àìïëèòóä-

íî-÷àñòîòíàÿ õàðàêòåðèñòèêà

(À×Õ):

(

)

(

)

Hje

-w

w= . Íà

ðèñ. 17.2, á èçîáðàæåíà À×Õ

èäåàëüíîãî ôèëüòðà íèæíèõ

÷àñòîò.

Ðåàëüíûå ôèëüòðû (ò. å.

ôèëüòðû, ñîñòîÿùèå èç ðåàëü-

íûõ ýëåìåíòîâ) èìåþò õàðàê-

445

max

-2

max

-2

min

()|

)

Ðèñ. 17.3

òåðèñòèêè ðàáî÷åãî îñëàáëåíèÿ è àìïëèòóäíî-÷àñòîòíóþ, îòëè÷íûå

îò èäåàëüíûõ.

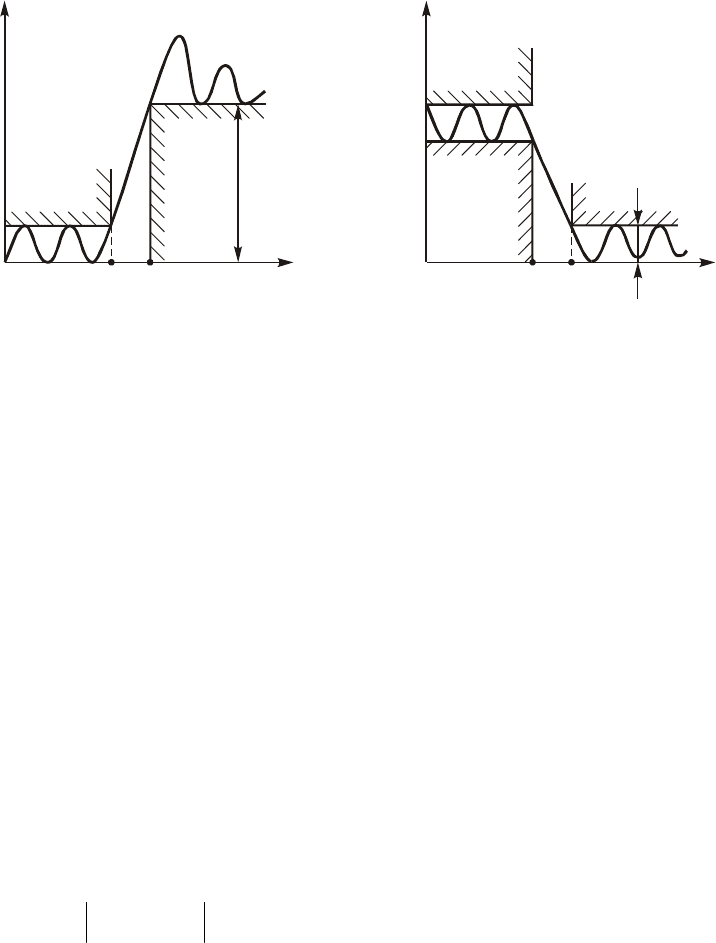
Òðåáîâàíèÿ ê ýëåêòðè÷åñêèì õàðàêòåðèñòèêàì ôèëüòðîâ çàäàþò-

ñÿ â âèäå äîïóñòèìûõ ïðåäåëîâ èçìåíåíèÿ ýòèõ õàðàêòåðèñòèê.

Òàê, ðàáî÷åå îñëàáëåíèå â ïîëîñå ïðîïóñêàíèÿ íå äîëæíî ïðåâû-

øàòü íåêîòîðîãî ìàêñèìàëüíîãî äîïóñòèìîãî çíà÷åíèÿ Àðmax, à â

ïîëîñå íåïðîïóñêàíèÿ íå äîëæíî áûòü íèæå íåêîòîðîãî ìèíèìàëü-

íî äîïóñòèìîãî çíà÷åíèÿ Àð min. Íåòðóäíî èçîáðàçèòü ýòè òðåáîâà-

íèÿ ãðàôè÷åñêè, êàê ýòî ñäåëàíî íà ðèñ. 17.3, à äëÿ ÔÍ×. Íà

ýòîì ðèñóíêå

$ ãðàíè÷íûå ÷àñòîòû ïîëîñ ïðîïóñêàíèÿ è

íåïðîïóñêàíèÿ.

Çíàÿ òðåáîâàíèÿ ê Àð , ìîæíî ïåðåñ÷èòàòü èõ â òðåáîâàíèÿ ê

À×Õ èëè, êàê ýòî ïðèíÿòî â òåîðèè ôèëüòðîâ, â òðåáîâàíèÿ ê

êâàäðàòó À×Õ (ðèñ. 17.3, á):

( )

,0,

max

min

<w<w

w>w

Õàðàêòåðèñòèêè ïðîåêòèðóåìûõ ôèëüòðîâ äîëæíû «óêëàäû-

âàòüñÿ» â ýòè òðåáîâàíèÿ (ðèñ. 17.3, à è á).

Ïîìèìî òðåáîâàíèé ê ÷àñòîòíîé çàâèñèìîñòè ðàáî÷åãî îñëàáëå-

íèÿ (à çíà÷èò, è ê À×Õ) ìîãóò çàäàâàòüñÿ òàêæå òðåáîâàíèÿ ê ôà-

çî÷àñòîòíîé õàðàêòåðèñòèêå ôèëüòðà (ñêàæåì, äîïóñòèìûå îòêëî-

íåíèÿ îò ëèíåéíîãî çàêîíà) è âåëè÷èíå íåëèíåéíûõ èñêàæåíèé

(îáóñëîâëåííûõ, íàïðèìåð, íàëè÷èåì æåëåçà â êàòóøêàõ èíäóê-

òèâíîñòè). Ìîãóò ïðåäúÿâëÿòüñÿ òðåáîâàíèÿ è ê äðóãèì õàðàêòåðè-

ñòèêàì è ïàðàìåòðàì ôèëüòðà. Íèæå áóäåì ó÷èòûâàòü òîëüêî òðå-

áîâàíèÿ ê ðàáî÷åìó îñëàáëåíèþ è À×Õ.

Èäåàëüíûå ÷àñòîòíûå õàðàêòåðèñòèêè ôèëüòðà (ñì. ðèñ. 17.2, à)

çàâåäîìî íåðåàëèçóåìû. ×àñòîòíûå õàðàêòåðèñòèêè ðåàëüíûõ

ôèëüòðîâ ìîãóò ëèøü ïðèáëèæàòüñÿ ê íèì ñ òîé èëè èíîé ñòåïå-

íüþ òî÷íîñòè â çàâèñèìîñòè îò ñëîæíîñòè ñõåìû ôèëüòðà.

446

17.2. Àïïðîêñèìàöèÿ õàðàêòåðèñòèê ôèëüòðîâ íèæíèõ ÷àñòîò

Ôóíêöèÿ ôèëüòðàöèè. Â îáùåì âèäå ýëåêòðè÷åñêèå ôèëüòðû

îïèñûâàþòñÿ ïåðåäàòî÷íîé ôóíêöèåé âèäà:

( )

110

apapapa

bpbpbpb

++++

. (17.1)

Êâàäðàò àìïëèòóäíî-÷àñòîòíîé õàðàêòåðèñòèêè òàêèõ ôèëüòðîâ

( )

2222

011

2222

011

cccc

dddd

w+w++w+

(17.2)

è, ñëåäîâàòåëüíî, ðàáî÷åå îñëàáëåíèå

2222

011

2222

011

10lg

dddd

cccc

æö

w+w++w+

ç÷

w+w++w+

èø

(17.3)

ìîãóò ïðè íàäëåæàùåì âûáîðå ñòåïåíè ïîëèíîìà (ïîðÿäêà ôèëüò-

ðà) è êîýôôèöèåíòîâ d

óäîâëåòâîðèòü çàäàííûì òðåáîâàíèÿ (ñì.

ðèñ. 17.3).

Â òåîðèè ôèëüòðîâ ïðèíÿòî èìåòü äåëî íå ñ îáû÷íîé óãëî-

âîé ÷àñòîòîé w, à ñ íîðìèðîâàííîé ÷àñòîòîé

W=ww

, ãäå

$ íîðìèðóþùàÿ ÷àñòîòà. Îáû÷íî â êà÷åñòâå íîðìèðóþùåé

÷àñòîòû âûáèðàþò ãðàíè÷íóþ ÷àñòîòó ïîëîñû ïðîïóñêàíèÿ

òàê ÷òî

ïïíïï

W=ww=ww=

Â òåîðèè ýëåêòðè÷åñêèõ ôèëüòðîâ âìåñòî ôîðìóë (17.2) è

(17.3) èñïîëüçóþò äðóãèå, òàêæå óíèâåðñàëüíûå äëÿ ëþáîãî òèïà

ôèëüòðà:

( )

HjW=

+eyW

; (17.4)

(

)

( )

10lg

A W=

éù

+eyW

ëû

. (17.5)

Ôóíêöèÿ

( )

íàçûâàåòñÿ ôóíêöèåé ôèëüòðàöèè, à e $ êîýô-

ôèöèåíòîì íåðàâíîìåðíîñòè îñëàáëåíèÿ. Â îáùåì ñëó÷àå y(W) $ ýòî

äðîáíî-ðàöèîíàëüíàÿ ôóíêöèÿ ñ âåùåñòâåííûìè êîýôôèöèåíòàìè (â

÷àñòíîñòè ïîëèíîì), óäîâëåòâîðÿþùàÿ óñëîâèÿì: $1 

(

)

 1 â

ïîëîñå ïðîïóñêàíèÿ è

(

)

. 1 â ïîëîñå íåïðîïóñêàíèÿ ôèëüòðà.

Â çàâèñèìîñòè îò âèäà ôóíêöèè ôèëüòðàöèè ïîëó÷àþò ðàçëè÷-

íûå òèïû ôèëüòðîâ. Åñëè â êà÷åñòâå ôóíêöèè ôèëüòðàöèè èñïîëü-

çóþò ïîëèíîìû, òî ôèëüòðû íàçûâàþòñÿ ïîëèíîìèàëüíûìè. Ñðåäè

ïîëèíîìèàëüíûõ ôèëüòðîâ øèðîêîå èñïîëüçîâàíèå íàøëè ôèëüò-

ðû Áàòòåðâîðòà è ×åáûøåâà. Åñëè

(

)

$ äðîáíî-ðàöèîíàëüíàÿ

ôóíêöèÿ, íàïðèìåð, äðîáü Çîëîòàðåâà, òî ïîëó÷àþò ôèëüòð Çî-

ëîòàðåâà. Âñå ýòè òðè òèïà ôèëüòðîâ áóäóò ðàññìîòðåíû â ýòîé

ãëàâå.

447

Ñëåäóåò îòìåòèòü, ÷òî èìååò ñìûñë ïîäðîáíî èçó÷àòü òîëüêî

ôèëüòðû íèæíèõ ÷àñòîò, ò. ê. äðóãèå òèïû ôèëüòðîâ (âåðõíèõ ÷àñ-

òîò, ïîëîñîâûå è çàãðàæäàþùèå) ìîãóò áûòü ëåãêî ïîëó÷åíû èç

ÔÍ× ñ ïîìîùüþ çàìåíû ïåðåìåííîé (÷àñòîòû). Äëÿ ýòîãî âî âñåõ

âûðàæåíèÿõ, ñîäåðæàùèõ ïåðåìåííóþ W, íóæíî ïðîèçâåñòè çàìå-

íó ïåðåìåííîé òàêèì îáðàçîì, ÷òîáû õàðàêòåðèñòèêè ÔÍ× Àð (W)

è |Hð(jW)|

ïðåîáðàçîâàëèñü â õàðàêòåðèñòèêè ñîîòâåòñòâóþùåãî

ôèëüòðà. Ïîäîáíàÿ çàìåíà ïåðåìåííîé W íàçûâàåòñÿ ïðåîáðàçîâà-

íèåì ÷àñòîòû, à èñõîäíûé ÔÍ× $ ôèëüòðîì Í×-ïðîòîòèïà.

Ïðåîáðàçîâàíèå ÷àñòîòû ïîçâîëÿåò óñòàíîâèòü ñîîòâåòñòâèå ìåæ-

äó ÷àñòîòàìè ïîëîñ ïðîïóñêàíèÿ è íåïðîïóñêàíèÿ Í×-ïðîòîòèïà è

÷àñòîòàìè ôèëüòðîâ âåðõíèõ ÷àñòîò, ïîëîñîâîãî èëè çàãðàæäàþùåãî,

à òàêæå ïðåîáðàçîâàòü ñõåìó ÔÍ× â ñõåìû ÔÂ×, ÏÔ èëè ÇÔ. Áî-

ëåå ïîäðîáíî âîïðîñû, ñâÿçàííûå ñ ïðåîáðàçîâàíèåì ÷àñòîòû, áóäóò

ðàññìàòðèâàòüñÿ â § 17.5.

Ôèëüòðû Áàòòåðâîðòà. Åñëè â âûðàæåíèÿõ, îïèñûâàþùèõ

êâàäðàò À×Õ ôèëüòðà (17.4) è åãî ðàáî÷åå îñëàáëåíèå (17.5), â êà-

÷åñòâå ôóíêöèè ôèëüòðàöèè èñïîëüçóþòñÿ ïîëèíîìû Áàòòåðâîð-

òà y(W) = B

(W) = W

(ïî èìåíè àâòîðà, ïðåäëîæèâøåãî èñ-

ïîëüçîâàòü èõ äëÿ «êîíñòðóèðîâàíèÿ» ÷àñòîòíûõ õàðàêòåðèñòèê

ôèëüòðà), òî òàêèå ôèëüòðû íàçûâàþòñÿ ôèëüòðàìè Áàòòåð-

âîðòà.

Èç ôîðìóë (17.4) è (17.5) ñëåäóåò, ÷òî äëÿ ôèëüòðîâ Áàòòåð-

âîðòà íà ÷àñòîòå W = 0 çíà÷åíèå êâàäðàòà À×Õ ðàâíî åäèíèöå, à

ðàáî÷åãî îñëàáëåíèÿ $ íóëþ. Ñ ðîñòîì ÷àñòîòû êâàäðàò À×Õ

ôèëüòðà Áàòòåðâîðòà óìåíüøàåòñÿ è ïàäàåò äî íóëÿ íà áåñêîíå÷íî

áîëüøîé ÷àñòîòå. Ðàáî÷åå îñëàáëåíèå ïëàâíî ðàñòåò äî áåñêîíå÷íî

áîëüøîãî çíà÷åíèÿ. Òàêèì îáðàçîì, âûðàæåíèÿ (17.4) è (17.5)

ïðèáëèæåííî âîñïðîèçâîäÿò õàðàêòåðèñòèêè èäåàëüíîãî ôèëüòðà.

×òîáû ýòè õàðàêòåðèñòèêè «âïèñûâàëèñü» â ïðåäúÿâëÿåìûå ê

ôèëüòðó òðåáîâàíèÿ (ñì. ðèñ. 17.3), íåîáõîäèìî èìåòü ðàáî÷åå îñ-

ëàáëåíèå (17.5) â ïîëîñå ïðîïóñêàíèÿ ìåíüøåå Àð max, à â ïîëîñå

íåïðîïóñêàíèÿ áîëüøåå Àð min. Ïåðâîìó óñëîâèþ ìîæíî óäîâëå-

òâîðèòü, åñëè ïîòðåáîâàòü íà ãðàíè÷íîé ÷àñòîòå ïîëîñû ïðîïóñêà-

íèÿ (W = 1) âûïîëíåíèÿ ðàâåíñòâà Àð (W)

W =1

= Àð max èëè

|Hð (jW)|

max

. Îòñþäà ñ ó÷åòîì (17.5) èëè (17.4) èìååì

1 + e

max

e è e

max

e $ 1. Âû÷èñëåííûé òàêèì ñïîñîáîì

êîýôôèöèåíò e:

max

e=-

(17.6)

íàçûâàåòñÿ êîýôôèöèåíòîì íåðàâíîìåðíîñòè îñëàáëåíèÿ â ïîëî-

ñå ïðîïóñêàíèÿ ôèëüòðà.

Â ôîðìóëå (17.6) âåëè÷èíà Àð max èìååò ðàçìåðíîñòü íåïåð. Åñ-

ëè âîñïîëüçîâàòüñÿ çíà÷åíèÿìè Àð max â äåöèáåëàõ, òî

448

max

-0,1

max

äÁ

min

-0,1

min

()|

)

= 6

= 4

= 2

0 1

= 2

= 4

= 6

Ðèñ. 17.4

0,1

101

max

e=-

. (17.7)

Ñ ó÷åòîì ââåäåííûõ îáîçíà÷åíèé êâàäðàò À×Õ ôèëüòðà Áàòòåð-

âîðòà çàïèøåòñÿ â âèäå

( )

(

)

HjW=+eW . (17.8)

Ýòà ôóíêöèÿ óäîâëåòâîðÿåò ñâîéñòâàì êâàäðàòà À×Õ ðåàëüíûõ ÷å-

òûðåõïîëþñíèêîâ, è ïîýòîìó åé ìîæíî ñîïîñòàâèòü ôèçè÷åñêè

îñóùåñòâèìûé ýëåêòðè÷åñêèé ôèëüòð.

Ðàáî÷åå îñëàáëåíèå ôèëüòðà Áàòòåðâîðòà:

( ) ( )

2222

ln1[H

ï];10lg1[äÁ]

AA=+eW=+eW . (17.9)

Êðóòèçíà ÷àñòîòíûõ õàðàêòåðèñòèê (17.8) è (17.9) çàâèñèò îò

ñòåïåíè m (ïîðÿäêà ôèëüòðà). ×åì áîëüøå ñòåïåíü m, òåì âûøå

êðóòèçíà õàðàêòåðèñòèê. Íà ðèñ. 17.4, à, è á ïîêàçàíû ãðàôèêè

ðàáî÷åãî îñëàáëåíèÿ è êâàäðàòà À×Õ ôèëüòðà Áàòòåðâîðòà äëÿ

ðàçëè÷íûõ m. Òàêèì îáðàçîì, äëÿ óäîâëåòâîðåíèÿ òðåáîâàíèé â

ïîëîñå íåïðîïóñêàíèÿ íåîáõîäèìî âûáðàòü ñîîòâåòñòâóþùèé

ïîðÿäîê ôèëüòðà m. Åãî ëåãêî îïðåäåëèòü èç óñëîâèÿ: íà ãðà-

íè÷íîé ÷àñòîòå ïîëîñû íåïðîïóñêàíèÿ: W

Àð (W

)  Àð min èëè

|Hð (jW)|



e . Ñ ó÷åòîì ýòîãî óñëîâèÿ ïîëó÷èì 1 +

+ e

, îòêóäà



(

)

min

. Ëîãàðèôìèðóÿ

îáå ÷àñòè íåðàâåíñòâà, ïðèäåì ê âûðàæåíèþ

2lnln

min

 .

Èç íåãî íàõîäèì îêîí÷àòåëüíî

m 

ln2ln

min

æö

ç÷

èø

. (17.10)

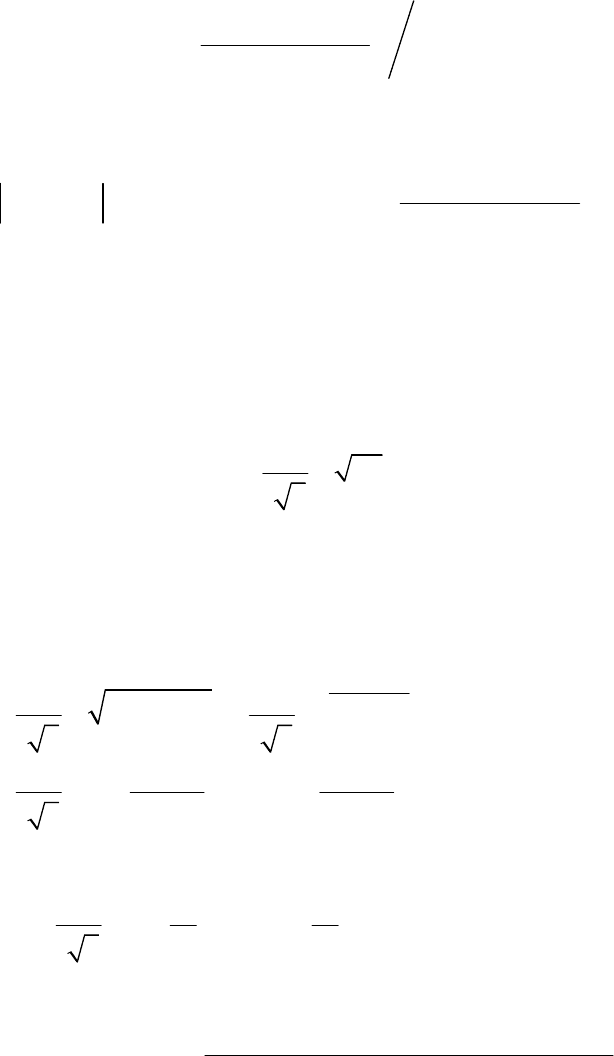
449

Âåëè÷èíà Àð min âõîäèò â ôîðìóëó â íåïåðàõ. Åñëè âû÷èñëÿòü åå â

äåöèáåëàõ, òî:

m 

0,1

101

lg2lg

min

æö

ç÷

èø

. (17.11)

Ïåðåäàòî÷íóþ ôóíêöèþ ôèëüòðà Áàòòåðâîðòà ìîæíî ïîëó÷èòü

èç (17.8), åñëè ïîëîæèòü jW = p:

( ) ( ) ( )

( )

ppp

HpHpHp

=-=

+e-

. (17.12)

è ðàçëîæèòü çíàìåíàòåëü ïîëó÷åííîé ôóíêöèè íà ïðîèçâåäåíèå

ñîìíîæèòåëåé.

Âû÷èñëèì êîðíè çíàìåíàòåëÿ, ò. å. ïîëþñû ôóíêöèè

Hð (p)´Hð ($p), îòäåëüíî äëÿ ÷åòíûõ è íå÷åòíûõ çíà÷åíèé m. Äëÿ

÷åòíûõ çíà÷åíèé m:

-e=

k = 1, 2, ..., 2m.

Òàê êàê:

(

)

( ) ( )

1cos21sin21

ekjk

-p

-==-p+-p

èìååì:

( )

(

)

12121

cossin,1,2,,2.

pee

jkm

-p

===

æö

=p+p=

ç÷

èø

(17.13)

Äëÿ íå÷åòíûõ çíà÷åíèé m:

cossin,1,2,,2.

pjkm

æö

=p+p=

ç÷

èø

Âûðàæåíèå (17.12) ïðèìåò âèä:

( ) ( )

( )( )

( )

122

HpHp

pppppp

e---

Ïîëîâèíà ïîëþñîâ ôóíêöèè Hð (p)Hð ($p) ëåæèò â ëåâîé ïîëó-

ïëîñêîñòè êîìïëåêñíîé ïåðåìåííîé p è ìîæåò áûòü îòíåñåíà ê ïå-

ðåäàòî÷íîé ôóíêöèè ðåàëèçóåìîãî ôèëüòðà Hð (p). Äðóãàÿ ïîëî-

âèíà ïîëþñîâ, ÿâëÿÿñü çåðêàëüíûì îòðàæåíèåì ïåðâîé, ðàñïîëàãà-

åòñÿ â ïðàâîé ïîëóïëîñêîñòè è îòíîñèòñÿ ê Hð ($p).

Ïîñòðîåííàÿ èç ïîëþñîâ, ëåæàùèõ â ëåâîé ïîëóïëîñêîñòè, ïå-

ðåäàòî÷íàÿ ôóíêöèÿ ôèëüòðà Áàòòåðâîðòà ÿâëÿåòñÿ ïîëèíîìèàëü-

íîé ïåðåäàòî÷íîé ôóíêöèåé òèïà (17.1):

450

( )

110

HpH

pbpbpb

++++

ãäå H = 1/e.

Ïðèìåð. Íàéòè âûðàæåíèÿ äëÿ ÷àñòîòíîé õàðàêòåðèñòèêè è ïåðåäàòî÷íîé

ôóíêöèè ôèëüòðà íèæíèõ ÷àñòîò Áàòòåðâîðòà, óäîâëåòâîðÿþùåãî ñëåäóþùèì

òðåáîâàíèÿì: À

ð max

= 3 äÁ; À

ð min

= 12,2 äÁ; f

= 159 êÃö; f

= 318 êÃö.

Îïðåäåëèì íîðìèðîâàííóþ ÷àñòîòó W

= f

= 2 è ïî ôîðìóëå (17.7)

êîýôôèöèåíò íåðàâíîìåðíîñòè îñëàáëåíèÿ e

= 10

0,1

$ 1 = 1. Ïîðÿäîê

ôèëüòðà íàéäåì ñîãëàñíî (17.11):

(

)

( )

0,112,2

lg1012lg22

 .

Âûáåðåì m = 2. Òîãäà â ñîîòâåòñòâèè ñ (17.8) è (17.9):

( )

;10lg1

HjAW==+W

Íàéäåì ïåðåäàòî÷íóþ ôóíêöèþ ôèëüòðà H

(p). Çíà÷åíèÿ ïîëþñîâ ôóíê-

öèè |H

(p)|

= H

(p) H

($p) = 1/(1 + ð

) âû÷èñëèì èç ôîðìóëû (17.13):

= 0,707 + j0,707; p

= $ 0,707 + j0,707; p

= $ 0,707 $ j0,707; p

= 0,707 $

$ j0,707. Ðàñïîëîæåíèå ïîëþñîâ â êîìïëåêñíîé ïëîñêîñòè ïîêàçàíî íà

ðèñ. 17.5, à.

Ïî òåîðåìå Âèåòà èç ïîëþñîâ â ëåâîé ïîëóïëîñêîñòè p

è p

ôîðìèðóåì

ïåðåäàòî÷íóþ ôóíêöèþ:

( )

1,411

pppp

e--

Èñïîëüçóÿ ââåäåííîå ðàíåå îáîçíà÷åíèå B

(W) = W

ïîëèíîìà

Áàòòåðâîðòà, ìîæíî ïðåäñòàâèòü ÷àñòîòíûå õàðàêòåðèñòèêè (17.8)

è (17.9) ôèëüòðà Áàòòåðâîðòà â ñëåäóþùåé ôîðìå:

( )

ln[

Íï],

10lg[

äÁ].

éù

+eW

ëû

éù

+eW

ëû

éù

+eW

ëû

(17.14)

Ôèëüòðû Áàòòåðâîðòà íàçûâàþò òàêæå ôèëüòðàìè ñ ìàêñèìàëü-

íî ïëîñêèì îñëàáëåíèåì â ïîëîñå ïðîïóñêàíèÿ (ñì. ðèñ. 17.4, à).

Ïîëèíîìèàëüíûå ôèëüòðû ×åáûøåâà. Åñëè â êà÷åñòâå ôóíê-

öèè ôèëüòðàöèè â (17.4) è (17.5) èñïîëüçîâàòü ïîëèíîì ×åáûøåâà,

îáîçíà÷àåìûé y(W) = T

(W), òî ôîðìóëû (17.14) ïðèìóò âèä:

( )

( ) ( )

11;

ln1[

Íï];

10lg1[

äÁ],

HjT

éù

W=+eW

ëû

éù

W=+eW

ëû

éù

W=+eW

ëû

(17.15)