Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.

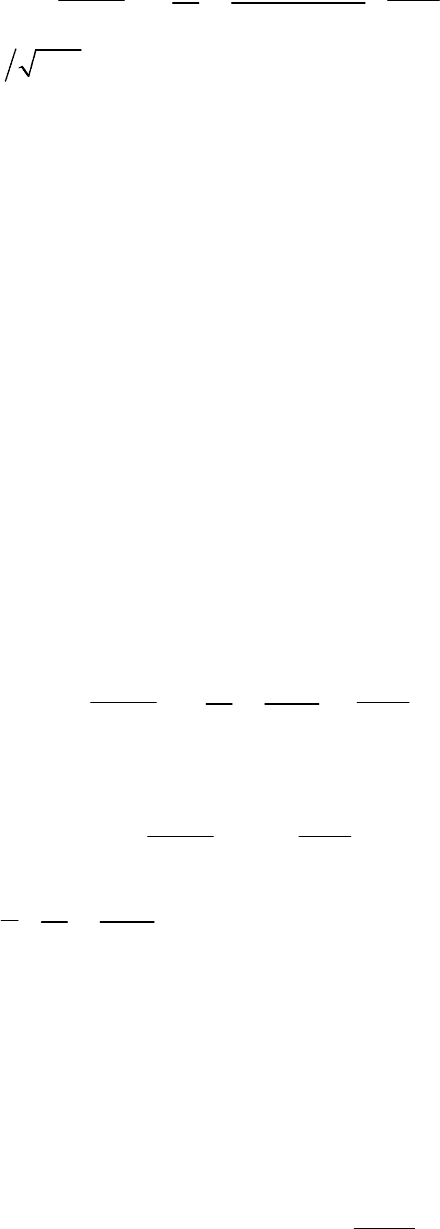
381
Ïîäñòàâèâ (15.7) â (15.6), ïîëó÷èì äèôôåðåíöèàëüíîå óðàâíå-
íèå àâòîãåíåðàòîðà
( )
2
2
êê
îñ
0 ê
2
0,
dudu
SM
u
G
u
dt
dt
CLC
éù
++w=
-
êú
ëû
(15.8)
ãäå
0
1
LC
w= $ ðåçîíàíñíàÿ ÷àñòîòà êîíòóðà.
Ýòî äèôôåðåíöèàëüíîå óðàâíåíèå ÿâëÿåòñÿ íåëèíåéíûì, òàê
êàê êîýôôèöèåíò ïðè ïåðâîé ïðîèçâîäíîé íàïðÿæåíèÿ u
ê
, â êîòî-
ðûé âõîäèò êðóòèçíà S(u
îñ
), íåëèíåéíî çàâèñèò îò íàïðÿæåíèÿ îá-
ðàòíîé ñâÿçè u
îñ
(èëè, ÷òî òî æå, îò èñêîìîé ïåðåìåííîé $ íà-
ïðÿæåíèÿ íà êîíòóðå). Óðàâíåíèå (15.8) îïðåäåëÿåò âñå ñâîéñòâà
àâòîãåíåðàòîðà è ïîçâîëÿåò óñòàíîâèòü óñëîâèÿ ñàìîâîçáóæäåíèÿ
êîëåáàíèé, îñîáåííîñòè ñòàöèîíàðíîãî ðåæèìà è õàðàêòåð ïåðå-
õîäíûõ ïðîöåññîâ â àâòîãåíåðàòîðå.
Óñëîâèå âîçíèêíîâåíèÿ êîëåáàíèé. Ïðè îïðåäåëåíèè óñëîâèé
ñàìîâîçáóæäåíèÿ ñëåäóåò ó÷åñòü, ÷òî àìïëèòóäà íàðàñòàþùèõ êî-
ëåáàíèé â àâòîãåíåðàòîðå äîñòàòî÷íî ìàëà è ðàáîòà àâòîãåíåðàòîðà
ïðîèñõîäèò íà ëèíåéíîì ó÷àñòêå ÂÀÕ òðàíçèñòîðà i
Ê
= F(u
îñ
).
Èíûìè ñëîâàìè, äëÿ ìàëûõ àìïëèòóä êîëåáàíèé ÂÀÕ ìîæíî àï-
ïðîêñèìèðîâàòü ëèíåéíî-ëîìàíîé ôóíêöèåé, êðóòèçíà êîòîðîé â
ðàáî÷åì äèàïàçîíå àìïëèòóä íàïðÿæåíèÿ ÿâëÿåòñÿ ïîñòîÿííîé, íå
çàâèñÿùåé îò íàïðÿæåíèÿ u
îñ
, ò. å. S(u
îñ
) = S.  ýòîì ñëó÷àå äèô-
ôåðåíöèàëüíîå óðàâíåíèå àâòîãåíåðàòîðà (15.8) ñòàíîâèòñÿ ëè-
íåéíûì:
2
2
êê
0ê
2
0.
dudu
GSM
u
dt
CLC
dt
æö
+×+w=
-
ç÷
èø
Ïåðåïèøåì åãî â âèäå
2
2
êê
ý0ê
2
20,
dudu
u
dt
dt
+a+w=
(15.9)
ãäå
ý
1
2
GSM
CLC
æö
a=
-
ç÷
èø
$ ýêâèâàëåíòíûé êîýôôèöèåíò çàòóõàíèÿ
êîëåáàòåëüíîãî êîíòóðà, âêëþ÷åííîãî â öåïü êîëëåêòîðà òðàíçè-
ñòîðà.
Ñîïîñòàâëåíèå óðàâíåíèÿ (15.9) ñ óðàâíåíèåì (15.2) äëÿ îäè-
íî÷íîãî êîëåáàòåëüíîãî êîíòóðà ïîêàçûâàåò, ÷òî ïðè âêëþ÷åíèè
êîëåáàòåëüíîãî êîíòóðà â êîëëåêòîðíóþ öåïü òðàíçèñòîðà êîýô-
ôèöèåíò çàòóõàíèÿ êîíòóðà a
ý
óìåíüøèòñÿ íà âåëè÷èíó SM/2LC,
çàâèñÿùóþ îò âçàèìîèíäóêöèè Ì, ò. å. îò ÎÑ:
ý
,
2
SM
LC
a=a-
ãäå a = G/2Ñ $ êîýôôèöèåíò çàòóõàíèÿ ñâîáîäíûõ êîëåáàíèé êîí-
òóðà.

382
G
C
L
SM
L
i
Ê
U
''
0
U
'
0
u
îñ
0
Ðèñ. 15.4 Ðèñ. 15.5
×òîáû â êîíòóðå âîçíèêëè íàðàñòàþùèå ïî àìïëèòóäå êîëåáà-
íèÿ, íåîáõîäèìî ñäåëàòü êîýôôèöèåíò a
ý
< 0. Ýòî âîçìîæíî ïðè
óñëîâèè SM/LÑ > G/C. Îòñþäà ïîëó÷àåì çíà÷åíèå êîýôôèöèåíòà
âçàèìíîé èíäóêöèè Ì ïðè êîòîðîì â êîëåáàòåëüíîì êîíòóðå âîç-
íèêíóò íàðàñòàþùèå ïî àìïëèòóäå êîëåáàíèÿ:
.
MLGS
>
(15.10)
Óñëîâèå (15.10) íàçûâàåòñÿ óñëîâèåì ñàìîâîçáóæäåíèÿ LC-àâ-
òîãåíåðàòîðà. Âåëè÷èíà M
êð
= LG/S íàçûâàåòñÿ êðèòè÷åñêèì
êîýôôèöèåíòîì âçàèìíîé èíäóêöèè. Êîëåáàíèÿ â àâòîãåíåðàòîðå
ìîãóò âîçíèêíóòü òîëüêî ïðè îáðàòíîé ñâÿçè ñ Ì > M
êð
. Ïðè
Ì < M
êð
êîýôôèöèåíò çàòóõàíèÿ êîíòóðà a
ý
> 0 è êîëåáàíèå â
êîíòóðå ñòàíîâèòñÿ çàòóõàþùèì. Êîýôôèöèåíò a
ý
â (15.9) ìîæíî
ïðåäñòàâèòü â ñëåäóþùåì âèäå:
(
)
ý
âí
2,
C
GG
a=
+
(15.11)
ãäå G
âí
= %(SM/L) $ ïðîâîäèìîñòü, âíîñèìàÿ â êîíòóð çà ñ÷åò
äåéñòâèÿ îáðàòíîé ñâÿçè. Çíàê êîýôôèöèåíòà Ì ìîæåò ìåíÿòüñÿ â
çàâèñèìîñòè îò íàïðàâëåíèÿ âêëþ÷åíèÿ (ñîãëàñíî èëè âñòðå÷íî)
âòîðè÷íîé îáìîòêè òðàíñôîðìàòîðà. Ïðè Ì > 0 âíîñèìàÿ ïðîâî-
äèìîñòü îêàçûâàåòñÿ îòðèöàòåëüíîé è åñëè åå âåëè÷èíà |G
âí
| > G,
÷òî èìååò ìåñòî ïðè Ì > M
êð
, òî a
ý
< 0 è â êîíòóðå âîçíèêíóò íà-
ðàñòàþùèå ïî àìïëèòóäå êîëåáàíèÿ. Ïîëîæèòåëüíûå çíà÷åíèÿ Ì ñî-
îòâåòñòâóþò ïîëîæèòåëüíîé ÎÑ, îòðèöàòåëüíûå $ îòðèöàòåëüíîé ÎÑ.
Ýêâèâàëåíòíàÿ ñõåìà êîëåáàòåëüíîãî êîíòóðà, ñîîòâåòñòâóþùàÿ
óðàâíåíèþ (15.9) ñ a
ý
èç (15.11), ïðèâåäåíà íà ðèñ. 15.4. Îòðè-
öàòåëüíàÿ îáùàÿ ïðîâîäèìîñòü êîíòóðà G + G
âí
< 0 ïðè Ì > M
êð
ñâèäåòåëüñòâóåò î òîì, ÷òî â êîíòóð ïîñòóïàåò ýíåðãèè áîëüøå, ÷åì
ðàñõîäóåòñÿ åå íà àêòèâíîé ïðîâîäèìîñòè êîíòóðà G.
Ñòàöèîíàðíûé ðåæèì ðàáîòû. Ïðè áîëüøèõ àìïëèòóäàõ ñèã-
íàëà íåëèíåéíîñòüþ ÂÀÕ òðàíçèñòîðà i
Ê
= F(u
îñ
) ïðåíåáðå÷ü óæå
íåëüçÿ: â îáùåì ñëó÷àå îíà äîëæíà àïïðîêñèìèðîâàòüñÿ ñòåïåííûì
ïîëèíîìîì âûñîêîãî ïîðÿäêà.
Òîê â öåïè êîëëåêòîðà â ñòàöèîíàðíîì ðåæèìå áóäåò èç-çà íå-
ëèíåéíîñòè ÂÀÕ íåñèíóñîèäàëüíîé ïåðèîäè÷åñêîé ôóíêöèåé âðå-
ìåíè è ìîæåò áûòü ïðåäñòàâëåí ðÿäîì Ôóðüå

383
U
m
îñ
U
m
îñ
0
0
SU
cp
()
m
îñ
SU
cp
()
m
îñ
à
)
á
)
Ðèñ. 15.6
Ê01020
coscos2
mm
iIItIt
=+w+w+
K
Ïàäåíèå íàïðÿæåíèÿ u
ê
íà êîëåáàòåëüíîì êîíòóðå, íàñòðîåííîì
íà ÷àñòîòó w
0
, îïðåäåëÿåòñÿ â îñíîâíîì ïåðâîé ãàðìîíèêîé êîëëåê-
òîðíîãî òîêà, òàê êàê ñîïðîòèâëåíèå êîíòóðà äëÿ òîêà ýòîé ãàðìî-
íèêè ÿâëÿåòñÿ íàèáîëüøèì (ðàâíûì R
îý
= l/G), à äëÿ îñòàëüíûõ
ãàðìîíèê $ äîñòàòî÷íî ìàëûì. Íàïðÿæåíèå ÎÑ u
îñ
, îïðåäåëÿåìîå
(15.5), âñëåäñòâèå ýòîãî òàêæå áóäåò ãàðìîíè÷åñêèì; åãî ìîæíî çà-
ïèñàòü â âèäå
ococ0
cos.
m
uUt
=w
Ââåäåì ïîíÿòèå ñðåäíåé êðóòèçíû ÂÀÕ
(
)
oc
cp1oc
.
m
mm
U
SIU=
Îíà îïðåäåëÿåòñÿ îòíîøåíèåì àìïëèòóäû I
m1
ïåðâîé ãàðìîíèêè
òîêà i
Ê
, ïðîòåêàþùåãî ÷åðåç íåëèíåéíûé ýëåìåíò, ê àìïëèòóäå
U
m îñ
, äåéñòâóþùåãî íà íåëèíåéíûé ýëåìåíò íàïðÿæåíèÿ u
îñ
.
Ñðåäíþþ êðóòèçíó ÷àñòî ïîýòîìó íàçûâàþò êðóòèçíîé ÂÀÕ ïî
ïåðâîé ãàðìîíèêå. Ñðåäíÿÿ êðóòèçíà S
cp
(U
m îñ
) çàâèñèò îò àìïëè-
òóäû íàïðÿæåíèÿ îáðàòíîé ñâÿçè U
m îñ
è îò ïîëîæåíèÿ ðàáî÷åé
òî÷êè U
0
. Íà ðèñ. 15.5 ïîêàçàíà òèïè÷íàÿ ÂÀÕ òðàíçèñòîðà i
Ê
=
= F(u
îñ
). Ïóñòü ðàáî÷àÿ òî÷êà âûáðàíà íà ñåðåäèíå ëèíåéíîãî ó÷à-
ñòêà õàðàêòåðèñòèêè (U
0
= U
0
¢). Ïðè óâåëè÷åíèè àìïëèòóäû íà-
ïðÿæåíèÿ U
m îñ
ñðåäíÿÿ êðóòèçíà, ïîêà ìû íàõîäèìñÿ â ïðåäåëàõ
ëèíåéíîãî ó÷àñòêà õàðàêòåðèñòèêè, îñòàåòñÿ íåèçìåííîé. Çàòåì
ñðåäíÿÿ êðóòèçíà ÂÀÕ ïàäàåò (ðèñ. 15.6, à). Åñëè âûáðàòü ðàáî-
÷óþ òî÷êó (U
0
= U
0
¢¢) íà íèæíåì çàãèáå õàðàêòåðèñòèêè i
Ê
=
= F(u
îñ
), ãäå ñðåäíÿÿ êðóòèçíà ìàëà, òî ïî ìåðå óâåëè÷åíèÿ àìïëè-
òóäû U
m îñ
áóäóò îõâàòûâàòüñÿ ó÷àñòêè õàðàêòåðèñòèêè ñ áîëüøåé
êðóòèçíîé è, ñëåäîâàòåëüíî, S
cp
(U
m îñ
) ñòàíåò ðàñòè. Ïîñëå ïðî-
õîæäåíèÿ ó÷àñòêà ñ íàèáîëüøåé êðóòèçíîé äàëüíåéøåå óâåëè÷åíèå
U
m îñ
ïðèâîäèò ê óìåíüøåíèþ ñðåäíåé êðóòèçíû (ðèñ. 15.6, á).
Äèôôåðåíöèàëüíîå óðàâíåíèå (15.8) ïðè ðàáîòå ãåíåðàòîðà â
ðåæèìå áîëüøèõ àìïëèòóä ÿâëÿåòñÿ, âîîáùå ãîâîðÿ, íåëèíåéíûì,
ïîñêîëüêó â êîýôôèöèåíò ïðè du
ê
/dt âõîäèò ñðåäíÿÿ êðóòèçíà
S
cp
(U
m îñ
), çàâèñÿùàÿ îò àìïëèòóäû U
m îñ
íàïðÿæåíèÿ ÎÑ. Îäíàêî

384
U
*
m
îñ
U
*
m
îñ
1
U
*
m
îñ
2
0
0
à
)
á
)
Â
Ñ
SU
cp
()
m
îñ
SU
cp
()
m
îñ
U
m
îñ
U
m
îñ
S
cp
*
S
cp
*
Ðèñ. 15.7
â ñòàöèîíàðíîì ðåæèìå, êîãäà ãàðìîíè÷åñêîå íàïðÿæåíèå íà êîí-
òóðå u
ê
õàðàêòåðèçóåòñÿ óñòàíîâèâøåéñÿ (ñòàöèîíàðíîé) àìïëèòó-
äîé U
m ê
, ãàðìîíè÷åñêîå íàïðÿæåíèå îáðàòíîé ñâÿçè u
îñ
òàêæå
îïèñûâàåòñÿ óñòàíîâèâøåéñÿ (ñòàöèîíàðíîé) àìïëèòóäîé U
m îñ
.
Ïðè ýòîì ñðåäíÿÿ êðóòèçíà S
cp
(U
m îñ
) ÿâëÿåòñÿ ïîñòîÿííîé âåëè-
÷èíîé è äèôôåðåíöèàëüíîå óðàâíåíèå (15.8) ìîæíî ñ÷èòàòü ëè-
íåéíûì:
(
)
2
2
oc
êê
cp
0 ê
2
0.
m
U
dudu
SM
G
u
dt
dt
CLC
éù
+×+w=
-
êú
ëû
(15.12)
 ñòàöèîíàðíîì ðåæèìå ãåíåðèðóþòñÿ íåçàòóõàþùèå ãàðìîíè-
÷åñêèå êîëåáàíèÿ. Ýòî èìååò ìåñòî, êîãäà
(
)
( )
oc
cp
ý
oc
cp
1
0.
22
m
m
U
M
SM
LG
G
U
S
LC
M
CLC
éù
éù
a===
-
-
êú
êú
ëû
ëû
Îòñþäà óñòàíîâèâøååñÿ (ñòàöèîíàðíîå) çíà÷åíèå ñðåäíåé êðó-
òèçíû ðàâíî
( )
( )
oc
cpcp
*
.
m
U
SS
LGM
==
Ñ ó÷åòîì ýòîãî îáîçíà÷åíèÿ êîýôôèöèåíò çàòóõàíèÿ êîíòóðà
ïåðåïèøåì â âèäå
( )
ý
oc
cpcp
*
.
2
m
M
U
SS
LC
éù
a=
-
ëû
(15.13)
Èç ôîðìóëû (15.13) ïðè a
ý
= 0 ìîæíî îïðåäåëèòü ñòàöèîíàð-
íóþ àìïëèòóäó
oc
*
m
U
, êîòîðàÿ ñîîòâåòñòâóåò òî÷êå ïåðåñå÷åíèÿ
êðèâîé S
ñð
(U
m îñ
) è ïðÿìîé ëèíèè
cp
*
S
. Ðèñ. 15.7 èëëþñòðèðóåò
ïðîöåññ íàõîæäåíèÿ ñòàöèîíàðíîé àìïëèòóäû äëÿ äâóõ çàâèñèìî-
ñòåé ñðåäíåé êðóòèçíû, ñîîòâåòñòâóþùèõ ðàçëè÷íûì ïîëîæåíèÿì
ðàáî÷åé òî÷êè íà ÂÀÕ (ñì. ðèñ. 15.5).
×àñòîòà ãåíåðèðóåìûõ êîëåáàíèé, îïðåäåëÿåìàÿ êàê w
ã
=
=
22
0
ý
w-a
, â ñòàöèîíàðíîì ðåæèìå ïðè a
ý
= 0 ñîâïàäàåò ñ ðåçî-
íàíñíîé ÷àñòîòîé êîëåáàòåëüíîãî êîíòóðà w
0
.
385
U
*
m
î
ñ
4
U
*
m
îñ4
U
*
m
î
ñ
3
U
*
m
îñ
3
U
*
m
îñ
U
*
m
î
ñ
5
U
*
m
îñ
5
U
*
m
î
ñ
6
U
*
m
îñ
6
0
0
à
)
á
)
SU
cp
()
m
îñ
U
m
îñ
S
cp1
*
S
cp2
*
S
cp3
*
S
cp4
*
S
cp5
*
S
cp6
*
M
1
M
2
M
3
M
4
M
5
M
6
M
1
M
2
M
3
M
4
M
5
M
6
M
Ðèñ. 15.8
Óñòîé÷èâîñòü ñòàöèîíàðíîãî ðåæèìà. Ñòàöèîíàðíûé ðåæèì íà-
çûâàåòñÿ óñòîé÷èâûì, åñëè îòêëîíåíèå DU
m îñ
îò ñòàöèîíàðíîé
àìïëèòóäû
oc
*
m
U
ñ òå÷åíèåì âðåìåíè áóäåò óìåíüøàòüñÿ.
Ðàññìîòðèì ñòàöèîíàðíûé ðåæèì â òî÷êå À íà ðèñ. 15.7, à. Îò-
êëîíåíèå %DU
m îñ
îò àìïëèòóäû
oc
*
m
U
ïðèâåäåò ê S
ñð
(U
m îñ
) >
cp
*
S
è, â ñîîòâåòñòâèè ñ (15.13), ê a
ý
< 0, ò. å. àìïëèòóäà êîëåáàíèé
áóäåò óâåëè÷èâàòüñÿ è ïðèáëèæàòüñÿ ê ñòàöèîíàðíîìó çíà÷åíèþ.
Ïðè îòêëîíåíèè +DU
mîñ
ñðåäíÿÿ êðóòèçíà S
ñð
(U
m îñ
) <
cp
*
S
, ò. å.
êîýôôèöèåíò çàòóõàíèÿ a
ý
, ñòàíåò ïîëîæèòåëüíûì è àìïëèòóäà
óìåíüøèòñÿ, âíîâü ïðèáëèæàÿñü ê ñòàöèîíàðíîé. Òàêèì îáðàçîì,
òî÷êà À ñîîòâåòñòâóåò óñòîé÷èâîìó ñòàöèîíàðíîìó ðåæèìó.
Òî÷êà  íà ðèñ. 15.7, á ñîîòâåòñòâóåò íåóñòîé÷èâîìó ðåæèìó,
òàê êàê îòêëîíåíèå àìïëèòóäû U
m îñ
îò ñòàöèîíàðíîãî çíà÷åíèÿ
oc
*
m
U
â ñòîðîíó óìåíüøåíèÿ âåäåò ê S
ñð
(U
m îñ
) <
cp
*
S
è a
ý
> 0, ò. å.
ê äàëüíåéøåìó óìåíüøåíèþ àìïëèòóäû U
m îñ
, à îòêëîíåíèå àìïëè-
òóäû U
m îñ
îò ñòàöèîíàðíîé â ñòîðîíó óâåëè÷åíèÿ âûçîâåò äàëü-
íåéøèé åå ðîñò è ïåðåõîä â ñëåäóþùåå ñòàöèîíàðíîå ñîñòîÿíèå,
îòìå÷åííîå òî÷êîé Ñ.
Ñòàöèîíàðíîå ñîñòîÿíèå â òî÷êå Ñ ÿâëÿåòñÿ óñòîé÷èâûì, â ÷åì
ëåãêî óáåäèòüñÿ ñ ïîìîùüþ ðàññóæäåíèé, àíàëîãè÷íûõ ïðèâåäåí-
íûì âûøå.
Ìîæíî çàìåòèòü, ÷òî ñïðàâåäëèâî ñëåäóþùåå óòâåðæäåíèå: ïå-
ðåñå÷åíèå ïðÿìîé ëèíèè
cp
*
S
ñ êðèâîé ñðåäíåé êðóòèçíû S
ñð
(U
m îñ
)
äàåò óñòîé÷èâûå çíà÷åíèÿ ñòàöèîíàðíîé àìïëèòóäû
oc
*
m
U
, åñëè íà
ýòîì ó÷àñòêå dS
ñð
(U
m îñ
)/dU
m îñ
< 0 è íåóñòîé÷èâûå çíà÷åíèÿ $
åñëè dS
ñð
(U
m îñ
)/dU
m îñ
> 0. Ïîýòîìó óñëîâèå dS
ñð
(U
m îñ
)/dU
m îñ
<
< 0 ìîæíî ñ÷èòàòü óñëîâèåì óñòîé÷èâîñòè ñòàöèîíàðíîãî ðå-
æèìà.
Ðåæèì ñàìîâîçáóæäåíèÿ. Áóäåì ìåíÿòü êîýôôèöèåíò âçàèìíîé
èíäóêöèè Ì è íàáëþäàòü çà ïðîöåññîì âîçíèêíîâåíèÿ êîëåáàíèé.
386
U
*
m
î
ñ
4
U
*
m
î
ñ
3
U
*
m
î
ñ
2
U
*
m
î
ñ
1
U
*
m
î
ñ
5
U
*
m
î
ñ
6
0
0
à
)
á
)
M
1
M
2
M
3
M
4
M
5
M
6
M
U
*
m
îñ
U
*
m
îñ4
U
*
m
îñ
2
SU
cp
()
m
îñ
S
cp1
*
S
cp2
*
S
cp3
*
S
cp4
*
S
cp5
*
S
cp6
*
M
1
M
2
M
3
M
4
M
5
M
6
U
*
m
îñ
Â
Ñ
Ðèñ. 15.9
Ýòîò ïðîöåññ çàâèñèò òàêæå îò âûáîðà ðàáî÷åé òî÷êè íà ÂÀÕ (íà-
ïðÿæåíèÿ ñìåùåíèÿ U
0
).
Âûáîðó ðàáî÷åé òî÷êè â îáëàñòè íàèáîëüøåé êðóòèçíû (íàïðÿ-
æåíèå ñìåùåíèÿ U
0
¢ íà ðèñ. 15.5) ñîîòâåòñòâóåò ãðàôèê ñðåäíåé
êðóòèçíû S
ñð
(U
m îñ
), ïîêàçàííîé íà ðèñ. 15.8, à.
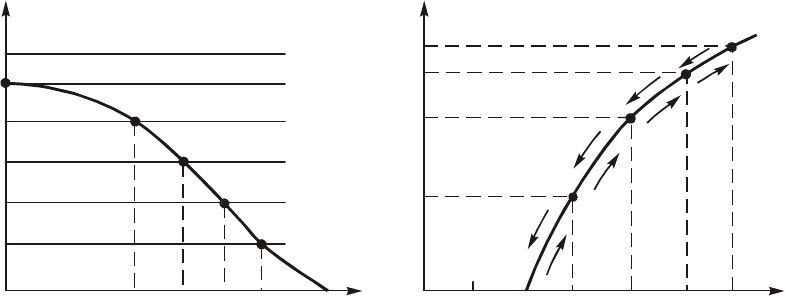
Ïðè èçìåíåíèè ïàðàìåòðà Ì ìåíÿåòñÿ çíà÷åíèå ñðåäíåé êðó-
òèçíû
cp
*
S
= LG/M. Íà ðèñ. 15.8, à èçîáðàæåíû íåñêîëüêî ïðÿìûõ
cp
*
S
, ñîîòâåòñòâóþùèõ ðàçëè÷íûì Ì.
Ïðè Ì = Ì
1
êîëåáàíèÿ â àâòîãåíåðàòîðå âîçíèêíóòü íå ìîãóò,
ïîñêîëüêó
cp
1
*
S
> S
ñð
(U
m îñ
) è êîýôôèöèåíò çàòóõàíèÿ êîíòóðà
a
ý
> 0, çíà÷èò, ëþáûå ñëó÷àéíûå ôëóêòóàöèè íàïðÿæåíèÿ U
m îñ
áóäóò áûñòðî çàòóõàòü.
Óâåëè÷åíèå Ì äî çíà÷åíèÿ Ì
2
ïðèâîäèò ê
cp
2
*
S
= S
ñð
(U
m îñ
) è
a
ý
= 0. Äàëüíåéøèé ðîñò Ì ñíèæàåò çíà÷åíèå
cp
*
S
; ïðè ýòîì êîýô-
ôèöèåíò a
ý
ñòàíîâèòñÿ îòðèöàòåëüíûì, ò. å. a
ý
< 0. Òàêèì îáðà-
çîì, íà÷èíàÿ ñ M
Ì
2
, â àâòîãåíåðàòîðå âîçíèêàþò íåçàòóõàþ-
ùèå êîëåáàíèÿ ñ ñîîòâåòñòâóþùèìè ñòàöèîíàðíûìè àìïëèòóäàìè
oc
*
m
U
. Ñ óâåëè÷åíèåì Ì ñòàöèîíàðíàÿ àìïëèòóäà êîëåáàíèé
oc
*
m
U
ïëàâíî íàðàñòàåò. Óìåíüøåíèå Ì âûçîâåò ïëàâíîå óìåíüøåíèå
çíà÷åíèé ñòàöèîíàðíîé àìïëèòóäû
oc
*
m
U
. Ãðàôèê çàâèñèìîñòè ñòà-
öèîíàðíîé àìïëèòóäû
oc
*
m
U
ãåíåðèðóåìûõ â àâòîãåíåðàòîðå êîëå-
áàíèé îò êîýôôèöèåíòà âçàèìíîé èíäóêöèè Ì ïðèâåäåí íà
ðèñ. 15.8, á. Òàêîé ðåæèì ñàìîâîçáóæäåíèÿ ãåíåðàòîðà, ïðè êîòî-
ðîì àìïëèòóäà êîëåáàíèé ïëàâíî íàðàñòàåò ñ óâåëè÷åíèåì Ì, íà-
çûâàåòñÿ ìÿãêèì ðåæèìîì ñàìîâîçáóæäåíèÿ.
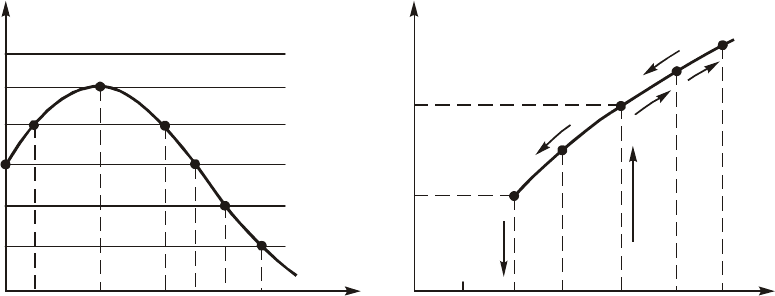
Åñëè ðàáî÷óþ òî÷êó âûáðàòü íà íèæíåì çàãèáå ÂÀÕ, êàê ýòî
ïîêàçàíî íà ðèñ. 15.5 ïðè U
0
= U
0
¢¢, òî ãðàôèê ñðåäíåé êðóòèçíû
S
ñð
(U
m îñ
) èìååò âèä, ïîêàçàííûé íà ðèñóíêå 15.9, à.
Ïðè Ì, ðàâíîì Ì
1
, Ì
2
è Ì
3
, íàëè÷èå ìàëûõ ôëóêòóàöèé íà-
ïðÿæåíèÿ U
m îñ
íå ïðèâåäåò ê óñòàíîâëåíèþ ñòàöèîíàðíîé àìïëè-
387
u
ÁÝ
C
Á
i
Á
R
Á
U
ïèò
U
0
U
0
C
u
ê
i
Ê
L
L
oc
u
oc
G
VT
M
0
t
a
)
á
)
0
+
-
+
Á
Ê
Ý
+
+
+
u
ÁÝ
u
ÁÝ
i
Ê
Ðèñ. 15.10
òóäû, ïîñêîëüêó ïðè çíà÷åíèÿõ
cp
*
S
, ðàâíûõ
cp
1
*
S
,
cp
2
*
S
è
cp
3
*
S , êî-
ýôôèöèåíò çàòóõàíèÿ êîíòóðà a
ý
áóäåò ïîëîæèòåëüíûì.
Òîëüêî íà÷èíàÿ ñ Ì = Ì
4
, êîãäà S
ñð
(U
m îñ
) =
cp4
*
S
è a
ý
= 0,
ìàëûå ôëóêòóàöèè àìïëèòóäû íàïðÿæåíèÿ îáðàòíîé ñâÿçè íà÷è-
íàþò áûñòðî ðàñòè, ïîêà íå óñòàíîâèòñÿ óñòîé÷èâîå ñòàöèîíàðíîå
çíà÷åíèå àìïëèòóäû
oc
*
m
U
. Äàëüíåéøåå óâåëè÷åíèå Ì âåäåò ê
ïëàâíîìó ðîñòó ñòàöèîíàðíîé àìïëèòóäû.
Ïðè ïëàâíîì óìåíüøåíèè îáðàòíîé ñâÿçè (êîýôôèöèåíòà Ì)
ñòàöèîíàðíàÿ àìïëèòóäà
oc
*
m
U
áóäåò òàêæå ïëàâíî óìåíüøàòüñÿ.
Êîëåáàíèÿ ñîðâóòñÿ ïðè çíà÷åíèè Ì = Ì
2
, ìåíüøåì Ì
4
, êîãäà ïå-
ðåñòàíåò âûïîëíÿòüñÿ óñëîâèå ñòàöèîíàðíîñòè S
ñð
(U
m îñ
) =
cp
*
S
.
Íà ðèñ. 15.9, á äàí ãðàôèê èçìåíåíèÿ àìïëèòóäû
oc
*
m
U
â çàâèñè-
ìîñòè îò Ì. Òàêîé ðåæèì, êîãäà êîëåáàíèÿ âîçáóæäàþòñÿ ïðè
áîëüøåì çíà÷åíèè Ì, à ñðûâàþòñÿ ïðè ìåíüøåì çíà÷åíèè Ì, íà-
çûâàåòñÿ æåñòêèì ðåæèìîì ñàìîâîçáóæäåíèÿ.
Äîñòîèíñòâîì ìÿãêîãî ðåæèìà ñàìîâîçáóæäåíèÿ ÿâëÿåòñÿ ïëàâ-
íîå èçìåíåíèå àìïëèòóäû
oc
*
m
U
ïðè èçìåíåíèè êîýôôèöèåíòà Ì;
äîñòîèíñòâîì æåñòêîãî ðåæèìà ÿâëÿåòñÿ âûñîêèé ÊÏÄ çà ñ÷åò ðà-
áîòû ñ îòñå÷êîé êîëëåêòîðíîãî òîêà.
Ìîæíî îáúåäèíèòü äîñòîèíñòâà ìÿãêîãî è æåñòêîãî ðåæèìîâ
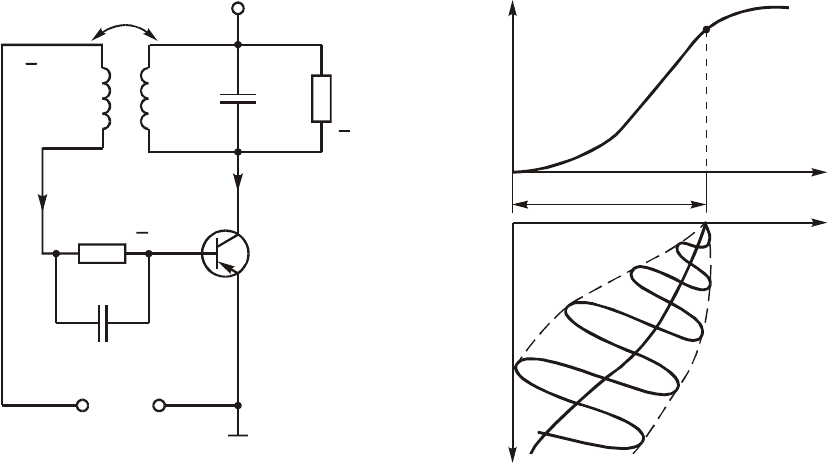
ñàìîâîçáóæäåíèÿ, åñëè ââåñòè â àâòîãåíåðàòîð öåïü àâòîìàòè÷å-
ñêîãî ñìåùåíèÿ R
Á
Ñ
Á
(ðèñ. 15.10, à). Èñõîäíîå ñìåùåíèå U
0
âû-
áèðàþò òàêèì, ïðè êîòîðîì ðàáî÷àÿ òî÷êà íàõîäèòñÿ íà ó÷àñòêå
íàèáîëüøåé êðóòèçíû ÂÀÕ, ÷òî ñîîòâåòñòâóåò ìÿãêîìó ðåæèìó.
Ïðè íàðàñòàíèè àìïëèòóäû êîëåáàíèé u
îñ
â öåïè áàçû çà ñ÷åò íå-
ëèíåéíîñòè ÂÀÕ i
Á
= F(u
ÁÝ
) ïðîèçîéäåò äåòåêòèðîâàíèå êîëå-
áàíèé. Âîçðàñòàíèå ïîñòîÿííîé ñîñòàâëÿþùåé òîêà áàçû I
ÁO
, êî-
òîðàÿ íà ðåçèñòèâíîì ñîïðîòèâëåíèè R
Á
ñîçäàåò íàïðÿæåíèå
388
U
âõ
R
âõ
S
U
âõ
R
âûõ
Z
ê
U
ê
Ðèñ. 15.11
I
ÁO
×R
Á
, ïðèâîäèò ê óìåíüøåíèþ ðåçóëüòèðóþùåãî íàïðÿæåíèÿ
ñìåùåíèÿ U
0
$ I
ÁO
×R
Á
è, êàê ðåçóëüòàò, ê ñäâèãó ðàáî÷åé òî÷êè
âëåâî (ðèñ. 15.10, á) ê íèæíåìó çàãèáó ÂÀÕ i
Ê
= F(u
ÁÝ
). Ïå-
ðåõîäíûé ïðîöåññ çàêàí÷èâàåòñÿ (ïðè ñîîòâåòñòâóþùåì çíà÷åíèè
R
Á
) óñòàíîâëåíèåì æåñòêîãî ñòàöèîíàðíîãî ðåæèìà ñ áîëåå âûñî-
êèì ÊÏÄ.
15.4. LC-ãåíåðàòîð ñ òðàíñôîðìàòîðíîé îáðàòíîé ñâÿçüþ.
Îïåðàòîðíûé è ÷àñòîòíûé ìåòîäû àíàëèçà
Õàðàêòåðèñòè÷åñêîå óðàâíåíèå. Îïåðàòîðíûé ìåòîä àíàëèçà
àâòîãåíåðàòîðà ñîñòîèò â èññëåäîâàíèè õàðàêòåðèñòè÷åñêîãî óðàâ-
íåíèÿ (14.11) öåïè ñ ÎÑ è âûÿâëåíèè èç ýòîãî óðàâíåíèÿ óñëîâèé
ñàìîâîçáóæäåíèÿ. Çàïèñàòü õàðàêòåðèñòè÷åñêîå óðàâíåíèå ãåíåðà-
òîðà ìîæíî áûëî áû íåïîñðåäñòâåííî ïî äèôôåðåíöèàëüíîìó
óðàâíåíèþ (15.9), îäíàêî ýòî ìîæíî ñäåëàòü è íå ïðèáåãàÿ ê ñî-
ñòàâëåíèþ äèôôåðåíöèàëüíîãî óðàâíåíèÿ. Ãåíåðàòîð êàê öåïü ñ
ÎÑ îïèñûâàåòñÿ õàðàêòåðèñòè÷åñêèì óðàâíåíèåì (ñì. ãë. 14):
(
)
(
)
óîñ
10.
HH
pp
-=
(15.14)
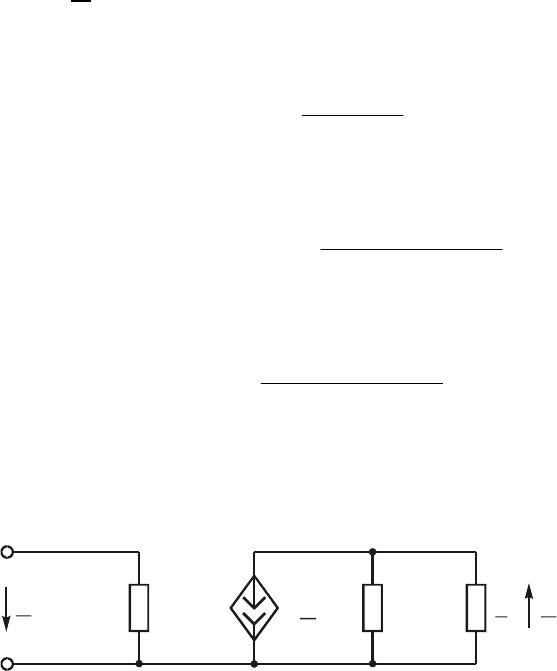
Ñõåìà çàìåùåíèÿ óñèëèòåëÿ íà òðàíçèñòîðå äàíà íà ðèñ. 15.11
(ñì. § 3.11). Çäåñü R
âõ
è R
âûõ
$ âõîäíîå è âûõîäíîå ñîïðîòèâëå-
íèÿ òðàíçèñòîðà; Z
ê
$ êîìïëåêñíîå ñîïðîòèâëåíèå ïàðàëëåëüíîãî
êîíòóðà.
Îïåðàòîðíàÿ ïåðåäàòî÷íàÿ ôóíêöèÿ òàêîãî óñèëèòåëÿ ðàâíà:
( )
(
)
( )
ê
ó
âõ
.
U
p
H
p
U
p
=-
 ñâîþ î÷åðåäü, èç ðèñ. 15.11 ñëåäóåò, ÷òî
( ) ( )
(
)
( )
âûõê
ê âõ
âûõê
.
RZ
p
USU
pp
RZ
p
=×
+
Ïîýòîìó
( )
(
)
( )
âûõê
ó
âûõê
.
SRZ
p
H
p
RZ
p
=-
+
Íà ïðàêòèêå â êà÷åñòâå óñèëèòåëüíîãî ýëåìåíòà èñïîëüçóþò òà-
êîé òðàíçèñòîð, ó êîòîðîãî R
âûõ
äîñòàòî÷íî âåëèêî.  ýòîì ñëó÷àå

389
(
)
(
)
óê
.
HSZ
pp
=-
(15.15)
Ó÷èòûâàÿ, ÷òî ñîïðîòèâëåíèå ïàðàëëåëüíîãî êîíòóðà
( )
(
)
ê
2
1
,
1
p
C
Z
p
G
pp
CLC
=
++
ïîëó÷àåì îêîí÷àòåëüíîå âûðàæåíèå ïåðåäàòî÷íîé ôóíêöèè óñèëè-
òåëÿ
( )
(
)
ó
2
1
,
1
Sp
C
H
p
G
pp
CLC
=-
++
Ïåðåäàòî÷íóþ ôóíêöèþ öåïè ÎÑ ëåãêî íàéòè, åñëè âñïîìíèòü
(ñì. § 15.5), ÷òî
() ()
îñê
,
M
uu
tt
L
=-
èëè äëÿ èçîáðàæåíèé ïî Ëàïëàñó
( ) ( )
îñê
.
M
UU
pp
L
=-
Îòñþäà
( )
(
)
( )
ê
îñ
îñ
.
U
p
M
H
p
UL
p
==-
Ïîñëå òîãî, êàê ïîëó÷åíû âûðàæåíèÿ äëÿ Íó(ð) è Í
îñ
(ð), õà-
ðàêòåðèñòè÷åñêîå óðàâíåíèå (15.14) ìîæíî çàïèñàòü â ñëåäóþùåì
âèäå:
2
10.
1
M
Sp
LC
G
pp
CLC
-=
++
Ïîñëå ïðîñòåéøèõ ïðåîáðàçîâàíèé ïîëó÷èì:
2
1
0,
GSM
pp
LC
CLC
æö
++=
-
ç÷
èø
(15.16)
èëè
22
ý0
20.
pp
+a+w=
 ðåæèìå ñàìîâîçáóæäåíèÿ ðàáî÷àÿ òî÷êà ðàñïîëàãàåòñÿ íà ëè-
íåéíîì ó÷àñòêå ÂÀÕ è, ñëåäîâàòåëüíî, êðóòèçíà S ÿâëÿåòñÿ ïî-
ñòîÿííîé âåëè÷èíîé.
Êîðíè õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ (15.16)
1,2
ýc
,
pj
=-a±w

390
0
ut
ê
()
t
0
ut
ê
()
t
(1)
(2)
j
w
0
a
p
1
p
2
(1)
(2)
a
ý
< 0
a
ý
= 0
Ðèñ. 15.12
ãäå
22
c0
ý
w=w-a
$ ÷àñòîòà ñâîáîäíûõ êîëåáàíèé â êîíòóðå.
×òîáû â ãåíåðàòîðå âîçíèêëè íåçàòóõàþùèå êîëåáàíèÿ êîðíè
äîëæíû ëåæàòü â ïðàâîé ïîëóïëîñêîñòè êîìïëåêñíîé ïåðåìåííîé ð
(ðèñ. 15.12, ñëó÷àé 1), ò. å. a
ý
< 0. Òàêèì îáðàçîì, óñëîâèå ñàìî-
âîçáóæäåíèÿ ïðèìåò âèä M > LG/S, ÷òî ñîâïàäàåò ñ âûðàæåíèåì
(15.10).
 ñòàöèîíàðíîì ðåæèìå ðàáîòû ãåíåðàòîðà êîðíè ïåðåìåùàþòñÿ
íà ìíèìóþ îñü êîìïëåêñíîé ïëîñêîñòè ð (ðèñ. 15.12, ñëó÷àé 2). Èç
óñëîâèÿ a
ý
= 0 ìîæíî íàéòè ñòàöèîíàðíîå çíà÷åíèå ñðåäíåé êðó-
òèçíû:
cp
*
.
SLGM
=
Àíàëèç â ÷àñòîòíîé îáëàñòè. Çàìåíÿÿ â âûðàæåíèÿõ äëÿ îïå-
ðàòîðíûõ ïåðåäàòî÷íûõ ôóíêöèé îïåðàòîð ð íà îïåðàòîð jw, çà-
ïèøåì ïåðåäàòî÷íóþ ôóíêöèþ öåïè ñ ðàçîìêíóòîé ÎÑ:
( ) ( ) ( )
( )
22
0
p óîñ
2
arctg
2
2
2
2
22
0
2
1
.
G
C
j
M
jS
LC
HHH
jjj
G
j
CLC
M
S
LC
e
G
C
æö
w
ç÷
p
-
ç÷
ç÷
w-w
èø
w
===
www
-w+w+
w
=
+w
w-w
Èç óñëîâèÿ áàëàíñà ôàç íà ÷àñòîòå ãåíåðàöèè
ã
22
0ã
arctg0
2
GC
w
p
-=
w-w
óáåæäàåìñÿ, ÷òî ãåíåðàòîð âîçáóæäàåòñÿ íà ÷àñòîòå w
ã
= w
0
.
Èç óñëîâèÿ áàëàíñà àìïëèòóä, êîòîðîå äîëæíî âûïîëíÿòüñÿ íà
÷àñòîòå ãåíåðàöèè
