Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.

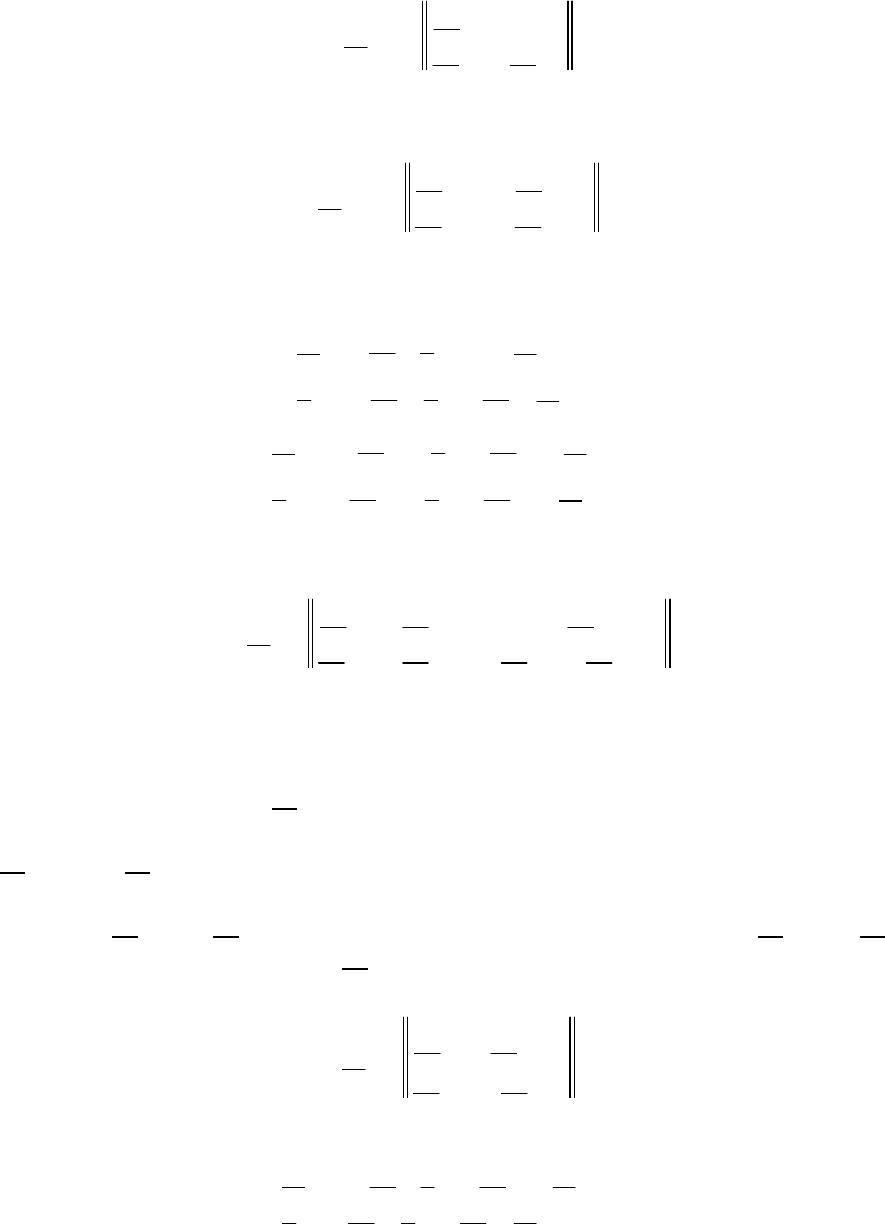
361
ìåòðû óñèëèòåëÿ íà ïðèìåðå ñõåìû, èçîáðàæåííîé íà ðèñ. 14.2.
Íà ðèñ. 14.5 èçîáðàæåíà ýêâèâàëåíòíàÿ ñõåìà ñ çàâèñèìûì èñòî÷-
íèêîì íàïðÿæåíèÿ ñ H-ïàðàìåòðàìè ïðè îòñóòñòâèè âíóòðåííåé
ÎÑ (H
12
= 0);
11
ó
2122
0
.
H
HH
=H
×åòûðåõïîëþñíèê ÎÑ ïðåäñòàâëåí â âèäå ÷åòûðåõïîëþñíèêà ñ
ìàòðèöåé H
îñ
-ïàðàìåòðîâ
11oc12oc
oc
21oc22oc
.
HH
HH
=H
Çàïèøåì ñîãëàñíî (12.5) óðàâíåíèÿ àêòèâíîãî è ïàññèâíîãî ÷å-
òûðåõïîëþñíèêîâ â H-ïàðàìåòðàõ:
111
1 âûõ
2
21122
âûõ
0
,
UHIU
IHIHU
=+×
ü
ï
ý
¢
=+
ï
þ
(14.5)
11oc112oc
oc âûõ
2
21oc122oc
âûõ
.
UHIHU
IHIHU
=+
ü
ï
ý
¢¢
=+
ï
þ
(14.6)
Ìàòðèöà H-ïàðàìåòðîâ ñëîæíîãî ÷åòûðåõïîëþñíèêà îïðåäåëÿåòñÿ
ñ ó÷åòîì § 12.3 êàê
1111oc12oc
2121oc2222oc
0
.
HHH
HHHH
++
=
++
H (14.7)
Ïîñêîëüêó â äàííîé ñõåìå (ðèñ. 14.5) ÎÑ ïðåäíàçíà÷åíà äëÿ
ïîëó÷åíèÿ íà âûõîäå ÷åòûðåõïîëþñíèêà îïðåäåëåííîãî íàïðÿæå-
íèÿ U
îñ
, òî îñíîâíîå çíà÷åíèå íà ñâîéñòâî óñèëèòåëÿ äîëæåí èã-
ðàòü êîýôôèöèåíò H
12îñ
. Ó÷èòûâàÿ, ÷òî öåïü ÎÑ îòáèðàåò ÷àñòü
ïîëåçíîé ýíåðãèè èç íàãðóçêè íåîáõîäèìî ñòðåìèòüñÿ, ÷òîáû
H
22îñ
=
H
22
. Êðîìå òîãî, äëÿ óìåíüøåíèÿ ïîòåðü âõîäíîãî ñèãíà-
ëà íà âõîäíîì ñîïðîòèâëåíèè öåïè ñ ÎÑ, íåîáõîäèìî âûïîëíåíèå
óñëîâèÿ H
11
?
H
11îñ
. Åñëè ïðè ýòîì ó÷åñòü, ÷òî îáû÷íî H
21
?
H
21îñ
è äëÿ ïàññèâíîé öåïè H
12îñ
< 1, òî îêîí÷àòåëüíî ìàòðèöà H-
ïàðàìåòðîâ ñëîæíîãî ÷åòûðåõïîëþñíèêà ñ öåïüþ ÎÑ ïðèìåò âèä
1112oc
2122
.
HH
HH
=H (14.8)
Ïðè ýòîì óðàâíåíèÿ ïåðåäà÷è H-ïàðàìåòðîâ ïðèìóò âèä (ðèñ. 14.5, á)
11112oc
âõ âûõ
221122
âûõ
.
UHIHU
IHIHU
=+
ü
ý
=+
þ
(14.9)
Ñ ïîìîùüþ ñèñòåìû óðàâíåíèé (14.9) ìîæíî îïðåäåëèòü èñêîìûå
çàâèñèìîñòè òîêîâ è íàïðÿæåíèé îò ïàðàìåòðîâ öåïè ÎÑ. Ìîæíî,

362
â ÷àñòíîñòè ïîêàçàòü, ÷òî îòðèöàòåëüíàÿ ÎÑ (ÎÎÑ) óìåíüøàåò êî-
ýôôèöèåíò ïåðåäà÷è ïî íàïðÿæåíèþ óñèëèòåëÿ â k-ðàç, à âõîäíîå
ñîïðîòèâëåíèå óâåëè÷èâàåò â k-ðàç, ãäå
(
)
(
)
12oc2111 ã 22í
1.
kHHHZHY
=-++
(14.10)
Òàê êàê ðàññìîòðåííûé òèï ÎÑ (ïîñëåäîâàòåëüíîé ïî íàïðÿ-
æåíèþ) âåäåò ê óâåëè÷åíèþ âõîäíîãî è óìåíüøåíèþ âûõîäíîãî
ñîïðîòèâëåíèé óñèëèòåëÿ, òî ýòî ïîçâîëÿåò îñóùåñòâèòü òðàíñ-
ôîðìàöèþ ñîïðîòèâëåíèé, ÷òî èñïîëüçóåòñÿ äëÿ ñîãëàñîâàíèÿ îò-
äåëüíûõ êàñêàäîâ óñèëèòåëÿ.
Ñëåäóåò òàêæå îòìåòèòü, ÷òî êîýôôèöèåíò ïåðåäà÷è ÎÓ ñ ïîñëå-
äîâàòåëüíîé ÎÑ ïî íàïðÿæåíèþ ïðè áåñêîíå÷íî áîëüøîì êîýôôè-
öèåíòå óñèëåíèÿ ÿâëÿåòñÿ ôóíêöèåé òîëüêî ïàðàìåòðîâ ýëåìåíòîâ
öåïè ÎÑ.
 çàêëþ÷åíèè ðàññìîòðèì âëèÿíèå ÎÑ íà ñòàáèëüíîñòü êîýô-
ôèöèåíòà óñèëåíèÿ, êàê îñíîâíîãî ïîêàçàòåëÿ óñèëèòåëÿ.
Äëÿ îòðèöàòåëüíîé è âåùåñòâåííîé ÎÑ ñîãëàñíî óðàâíåíèþ
(14.4) äëÿ êîýôôèöèåíòà óñèëåíèÿ óñèëèòåëÿ ìîæíî çàïèñàòü
ó
óoc
.
1
H
H
HH
=
+×
(14.11)
Ïðîäèôôåðåíöèðóåì (14.11) ïî H
ó
è H
îñ
( )
( )
2
ó
2
óocóoc
óoc
1
;.
1
1
H
dHdH
dHdHHH
HH
==
+
+
(14.12)
Îòñþäà îòíîñèòåëüíàÿ íåñòàáèëüíîñòü êîýôôèöèåíòà óñèëåíèÿ ñ
ó÷åòîì (14.11) áóäåò ðàâíà
( )
ó
óocó
1
,
1
dH
dH
HHHH
éù
=
êú
+
ëû
(14.13)
( )
oc
óococ
1
.
11
dHdH
HHHH
éù
=
êú
+
ëû
(14.14)
Àíàëèç (14.13) ïîêàçûâàåò, ÷òî íåñòàáèëüíîñòü êîýôôèöèåíòà óñè-
ëåíèÿ óñèëèòåëÿ ñ ÎÑ â
(
)
ó
oc
11 HH
+×
ðàç ìåíüøå ÷åì áåç ÎÑ.
Ðàâåíñòâî (14.14) ïîêàçûâàåò, ÷òî ïðè
ó
oc
1
HH
?
dH
»
ococ
dHH
»
, ò. å. ïðîïîðöèîíàëüíî íåñòàáèëüíîñòè êîýôôèöèåíòà
ïåðåäà÷è öåïè ÎÑ, ïîýòîìó ñòàðàþòñÿ öåïü ÎÑ ñäåëàòü äîñòàòî÷íî
ñòàáèëüíîé.
Àíàëîãè÷íûì îáðàçîì ìîæíî íàéòè êîýôôèöèåíò ïåðåäà÷è è
èññëåäîâàòü âëèÿíèå ÎÑ íà ïàðàìåòðû äðóãèõ ñõåì ñ ÎÑ (ñì.
ðèñ. 14.1 á)%ã)). Ïðè ýòîì íàäî èìåòü ââèäó, ÷òî â ñîîòâåòñòâóþ-
ùèõ âûðàæåíèÿõ áóäóò ôèãóðèðîâàòü íå òîëüêî êîìïëåêñíûå êî-
ýôôèöèåíòû ïåðåäà÷è ïî íàïðÿæåíèþ, íî è ïî òîêó, à òàêæå ïåðå-
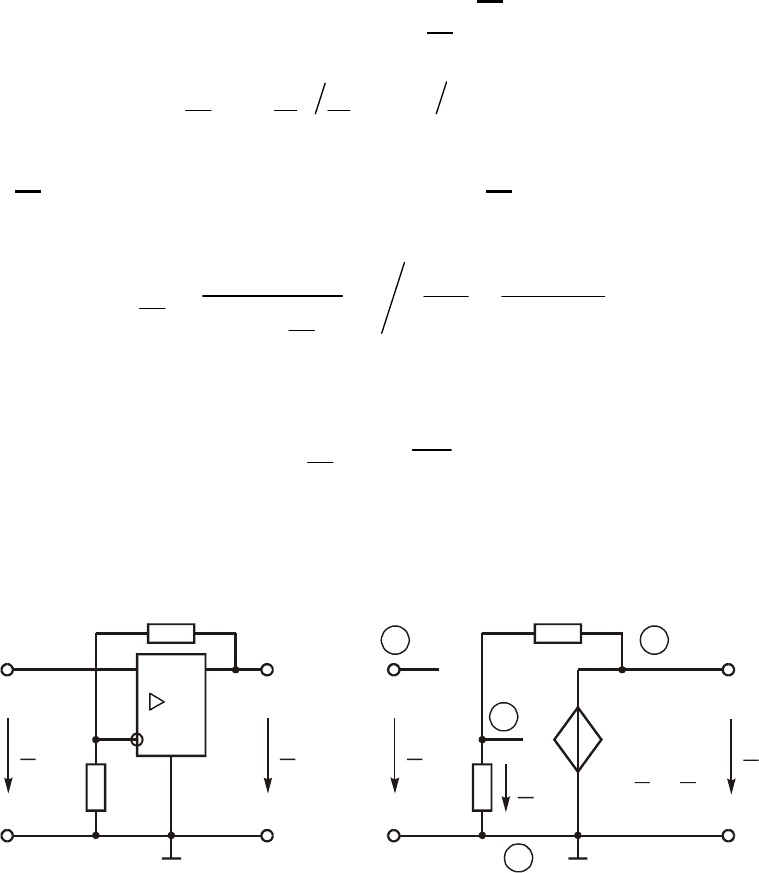
363
H
u
R
0
R
1
U
2
U
1
H
u
R
0
R
1
U
2
U
1
U
3
1
2
3
4
+
(
U
1
U
3
)
_
à
)
á
)
Ðèñ. 14.6
äàòî÷íûå êîìïëåêñíûå ñîïðîòèâëåíèÿ è ïðîâîäèìîñòè. Êðîìå òîãî
óðàâíåíèÿ ïåðåäà÷è ñîîòâåòñòâóþùèõ ÷åòûðåõïîëþñíèêîâ â çàâè-
ñèìîñòè îò òèïà ñîåäèíåíèÿ äîëæíû áûòü çàïèñàíû â Z èëè F-
ïàðàìåòðàõ (ñì. § 12.2).
14.3. Ïðèìåðû öåïåé ñ îáðàòíîé ñâÿçüþ
Ìàñøòàáíûé óñèëèòåëü ñ íåèíâåðòèðóþùèì âõîäîì. Íà ðèñ. 14.6,
à èçîáðàæåíà öåïü íà ÎÓ, ïðåäíàçíà÷åííàÿ äëÿ ìàñøòàáèðîâàíèÿ
íàïðÿæåíèÿ, à íà ðèñ. 14.6, á $ åå ñõåìà çàìåùåíèÿ ñ çàâèñèìûì
èñòî÷íèêîì òèïà ÈÍÓÍ.  ãë. 2 äàííàÿ ñõåìà àíàëèçèðîâàëàñü
ìåòîäîì óçëîâûõ ïîòåíöèàëîâ. Ïîëó÷èì ïåðåäàòî÷íóþ ôóíêöèþ
ýòîé öåïè êàê öåïè ñ îáðàòíîé ñâÿçüþ, èñïîëüçóÿ ôîðìóëó (14.4).
Öåïüþ îáðàòíîé ñâÿçè íà ñõåìå ðèñ. 14.6 ñëóæèò Ã-îáðàçíûé äå-
ëèòåëü íàïðÿæåíèÿ, ñîñòàâëåííûé èç ðåçèñòèâíûõ ñîïðîòèâëåíèé R
0
è R
1
. Âûõîäíîå íàïðÿæåíèå óñèëèòåëÿ U
2
ïîñòóïàåò íà âõîä öåïè
ÎÑ (óçëû 2%4); íàïðÿæåíèå ÎÑ U
3
ñíèìàåòñÿ ñ ðåçèñòîðà R
1
(óçëû 3%4). Ïåðåäàòî÷íàÿ ôóíêöèÿ ïî íàïðÿæåíèþ öåïè ÎÑ
(
)
101
oc
32
.
HUURRR
==+
Âîñïîëüçóåìñÿ ôîðìóëîé (14.4) è ó÷òåì, ÷òî âõîäíîå íàïðÿ-
æåíèå U
1
è íàïðÿæåíèå îáðàòíîé ñâÿçè U
3
íå ñóììèðóþòñÿ, à âû-
÷èòàþòñÿ. Òîãäà ïîëó÷èì ïåðåäàòî÷íóþ ôóíêöèþ ìàñøòàáíîãî
óñèëèòåëÿ:
1
01
oc
1
1.
1
u
u
u
H
R
H
HRR
HH
æö
==+
ç÷
+
+
èø
Ó÷èòûâàÿ, ÷òî â ðåàëüíûõ ÎÓ çíà÷åíèå
1
u
H
?
, îêîí÷àòåëüíî
èìååì:
0
1
1,
R
H
R
=+
÷òî, åñòåñòâåííî, ñîâïàäàåò ñ ðåçóëüòàòîì, ïîëó÷åííûì â ãë. 2 ìå-
òîäîì óçëîâûõ íàïðÿæåíèé.
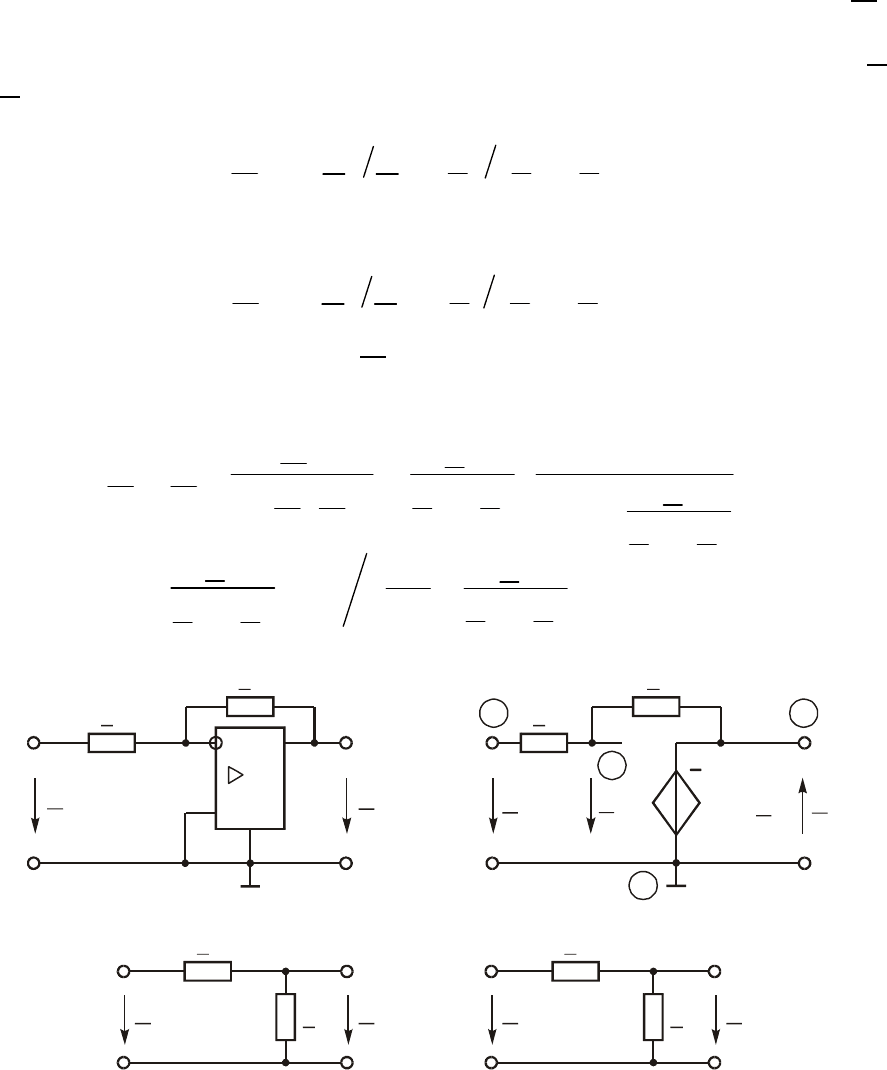
364
H
u
U
2
U
1
H
u
U
2
U
1
U
3
1
2
3
4
+
U
3
_
à
)
á
)
Z
1
Z
0
Z
1
Z
0
Z
1
U
1
1
U
3
Z
0
3
44
Z
0
U
2
2
U
3
Z
1
3
4
4
Âõîäíàÿ öåïüÖåïü ÎÑ
â
)
ã
)
Ðèñ. 14.7
Çâåíî íà ÎÓ ñ ÷àñòîòíî-çàâèñèìîé ÎÑ. Çâåíî òàêîãî âèäà ïðåä-
ñòàâëåíî íà ðèñ. 14.7, à, à åãî ñõåìà çàìåùåíèÿ $ íà ðèñ. 14.7, á.
×òîáû ïðîàíàëèçèðîâàòü ïðÿìîé ïóòü ïðîõîæäåíèÿ ñèãíàëà è ïóòü
ïðîõîæäåíèÿ ñèãíàëà ÎÑ, íåîáõîäèìî âîñïîëüçîâàòüñÿ ìåòîäîì
íàëîæåíèÿ (ñì. § 2.3). Äëÿ ýòîãî ñëåäóåò ïîî÷åðåäíî èñêëþ÷àòü
èñòî÷íèêè âõîäíîãî íàïðÿæåíèÿ è íàïðÿæåíèÿ îáðàòíîé ñâÿçè, çà-
ìåíÿÿ èõ âíóòðåííèì ñîïðîòèâëåíèåì.  ñëó÷àå èäåàëüíûõ èñòî÷-
íèêîâ íàïðÿæåíèÿ (ðèñ. 14.17, á) èõ âíóòðåííåå ñîïðîòèâëåíèå
ðàâíî íóëþ. Èç ñõåìû çàìåùåíèÿ ñëåäóåò, ÷òî íàïðÿæåíèå U
1
,
ïðèëîæåííîå ê çâåíó, îñëàáëÿåòñÿ âõîäíîé öåïüþ, ïðåäñòàâëÿþ-
ùåé ñîáîé Ã-îáðàçíûé äåëèòåëü íàïðÿæåíèÿ ñ ñîïðîòèâëåíèÿìè Z
1
è Z
0
â ïëå÷àõ (ðèñ. 14.7, â). Ïåðåäàòî÷íàÿ ôóíêöèÿ ïî íàïðÿæå-
íèþ òàêîãî äåëèòåëÿ ðàâíà
(
)
âõ001
31
.
HUUZZZ
==+
Öåïü îáðàòíîé ñâÿçè (ðèñ. 14.7, ã) òàêæå ÿâëÿåòñÿ Ã-îáðàçíûì
÷åòûðåõïîëþñíèêîì ñ ïåðåäàòî÷íîé ôóíêöèåé
(
)
oc101
23
.
HUUZZZ
==+
Êîýôôèöèåíò óñèëåíèÿ ÎÓ H
ó
= $H
u
.
 ñîîòâåòñòâèè ñ ôîðìóëîé (14.4) ïîëó÷àåì, ïåðåäàòî÷íóþ
ôóíêöèþ çâåíà:
( )
ó
0
âõ
1
óoc01
01
0
1
01
01
1
1
1
1.
u
u
u
H
Z
H
HH
Z
HHZZ
H
ZZ
Z
Z
HZZ
ZZ
-
==×=
-+
+
+
æö
=×-+
ç÷
+
+
èø
365
U
2
U
1
R
U
âõó
R
K
à
)
C
C
U
2
U
1
R
R
á
)
C
C
1
2
4
3
+
U
3
H
u
U
3
U
1
R
U
âõó
R
â
)
C
1
5
3
5
C
U
2
R
U
âõó
R
ã
)
C
4
5
3
5
C
5
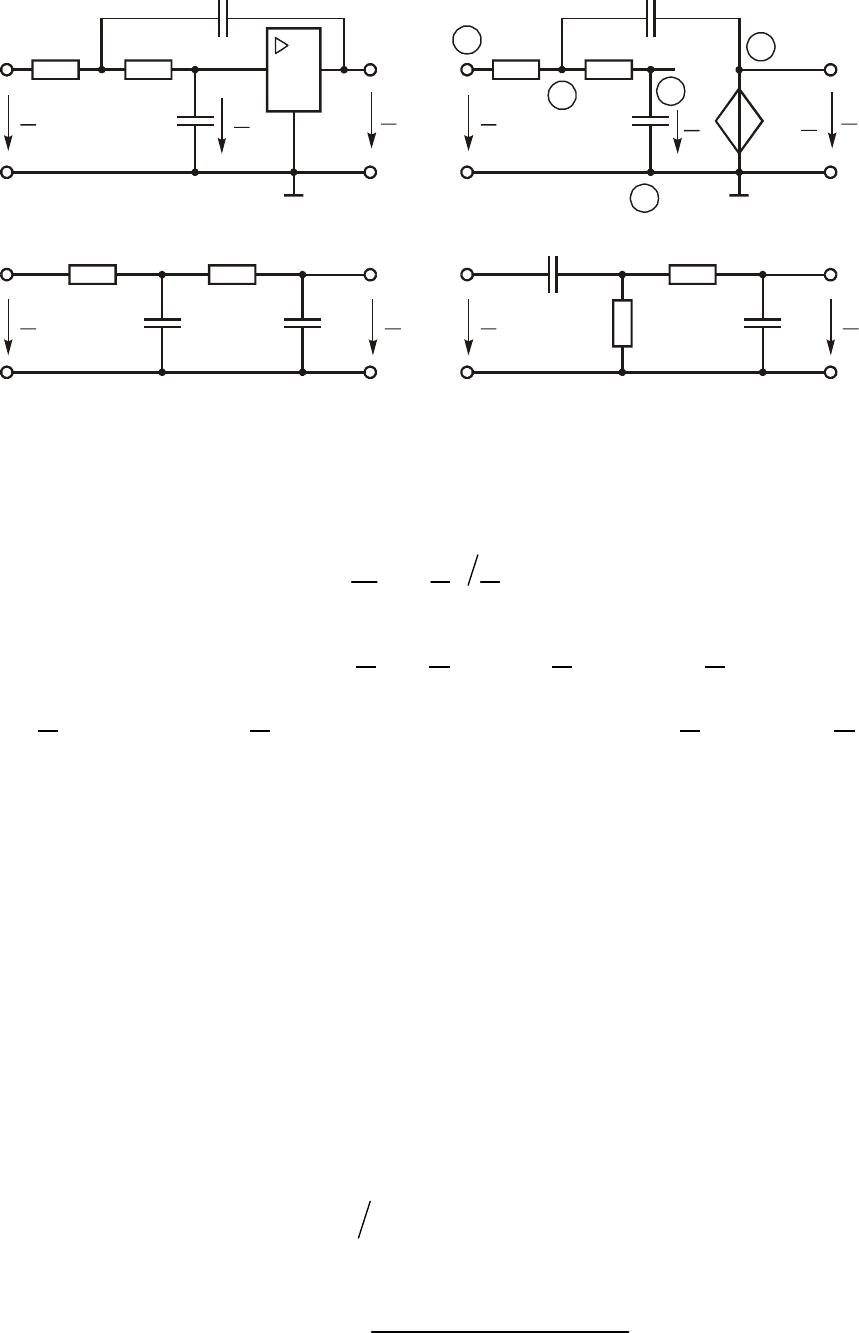
Ðèñ. 14.8
Ó÷èòûâàÿ, ÷òî
1
u
H
?
, ïîëó÷àåì:
01
.
HZZ
=-
(14.15)
Äàííîå çâåíî ìîæåò âûïîëíÿòü ðàçëè÷íûå ôóíêöèè â çàâèñèìî-
ñòè îò âèäà ñîïðîòèâëåíèé Z
0
è Z
1
. Ïðè Z
0
= R
0
è Z
1
= R
1
çâåíî
ïðåâðàùàåòñÿ â èíâåðòèðóþùèé ìàñøòàáíûé óñèëèòåëü (ñì. ãë. 2);
ïðè Z
0
= l
/
jwC è Z
1
= R $ â èíòåãðàòîð; ïðè Z
0
= R è Z
1
=
= l
/
jwC $ â äèôôåðåíöèàòîð (ñì. ãë. 3).
Çâåíî âòîðîãî ïîðÿäêà ñ ðåãóëèðóåìûì êîýôôèöèåíòîì óñèëå-
íèÿ. Ñõåìà çâåíà ïîêàçàíà íà ðèñ. 14.8, à. Óñèëèòåëü ñ ðåãóëèðóå-
ìûì êîýôôèöèåíòîì óñèëåíèÿ Ê ìîæåò áûòü âûïîëíåí ëèáî íà
òðàíçèñòîðíûõ êàñêàäàõ, ëèáî íà ÎÓ ïî ñõåìå ðèñ. 14.6, a, ëèáî
íà äðóãèõ àêòèâíûõ ýëåìåíòàõ. Â ñõåìå çàìåùåíèÿ íà ðèñ. 14.8, á
îí ïðåäñòàâëåí èäåàëüíûì ÈÍÓÍ.
Àíàëèç ïðîõîæäåíèÿ âõîäíîãî ñèãíàëà è ñèãíàëà â öåïè ÎÑ
ïîêàçûâàåò, ÷òî çâåíî èìååò âõîäíóþ öåïü, èçîáðàæåííóþ íà
ðèñ. 14.8, â è öåïü ÎÑ, ïîêàçàííóþ íà ðèñ. 14.8, ã. Ïåðåäàòî÷íûå
ôóíêöèè ýòèõ öåïåé ìîæíî ïîëó÷èòü ìàòðè÷íûì ìåòîäîì (ñì.
ãë. 12), íàïðèìåð, ðàññìàòðèâàÿ êàæäóþ öåïü êàê êàñêàäíîå ñîåäè-
íåíèå ñîîòâåòñòâóþùèõ Ã-îáðàçíûõ ÷åòûðåõïîëþñíèêîâ.
Äëÿ âõîäíîé öåïè (ñì. § 3.11)
( )
(
)
222
âõ
131.
HppRCpRC=++
(14.16)
Äëÿ öåïè ÎÑ
( )
oc
222
.
31
pRC
Hp
pRCpRC
=
++
(14.17)
Ñ ó÷åòîì (14.3) ïîëó÷èì ïåðåäàòî÷íóþ ôóíêöèþ çâåíà
366
-
b
m-
2
a
n
å
-
b
m-
1
å
ò
ò
-
b
1
a
1
å
ò
-
b
0
a
0
å
U
2
U
1
Ðèñ. 14.9
( ) ( )
(
)
( ) ( )
ó
âõ
óîñ
.
1
Hp
HpHp
HpHp
=×
-
(14.18)
Êîýôôèöèåíò ïåðåäà÷è óñèëèòåëÿ Í
ó
(ð) = Ê. Òîãäà, ïîäñòàâ-
ëÿÿ (14.6) è (14,7) â (14.8), ïîñëå ïðåîáðàçîâàíèé èìååì
( )
( )
(
)
222
31.
HpKpRCpRCK=+-+
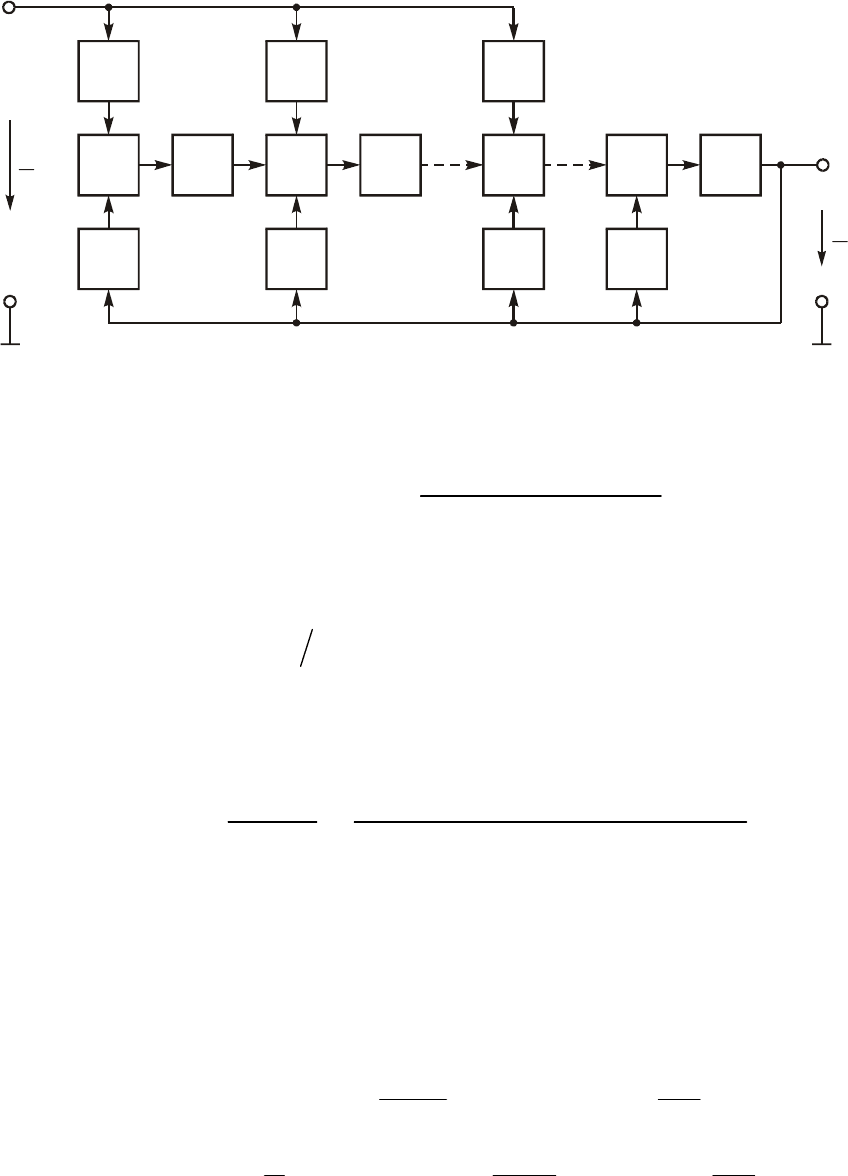
Ìîäåëèðîâàíèå ïåðåäàòî÷íûõ ôóíêöèé îáùåãî âèäà. Ïåðåäà-
òî÷íàÿ ôóíêöèÿ ëèíåéíîé öåïè ïðåäñòàâëÿåòñÿ ñîãëàñíî (7.41) â
âèäå ðàöèîíàëüíîé äðîáè:
( )
( )
( )
1
2
110
1
1
110
.
nn
nn
u
mm
m
Up
apapapa
Hp
Up
pbpbpb
-
-
-
-
++++
==
++++
K
K
(14.19)
Ïðèâåäÿ (14.9) ê îáùåìó çíàìåíàòåëþ, ïîëó÷èì:
( )
(
)
( )
( )
1
2110
1
1110
.
mm
m
nn
nn
Uppbpbpb
Upapapapa
-
-
-
-
++++=
=++++
K
K
Ýòî ðàâåíñòâî ìîæíî ïåðåïèñàòü â âèäå
( ) ( ) ( )
( ) ( ) ( )
2110
212120
1
11
111
.
n
mnm
m
mm
UpUpaUpa
pp
UpbUpbUpb
p
pp
-
-
-
=++-
----
K
K
Òàê êàê îïåðàöèè l
/
p
m
ñîîòâåòñòâóåò m-êðàòíîå èíòåãðèðîâàíèå,
òî ïîñëåäíåìó óðàâíåíèþ ñîîòâåòñòâóåò ñòðóêòóðíàÿ ñõåìà, èçî-
áðàæåííàÿ íà ðèñ. 14.9.
Òàêèì îáðàçîì, ñ ïîìîùüþ èíòåãðàòîðîâ, ñóììàòîðîâ, ìàñøòàá-
íûõ óñèëèòåëåé, óìíîæèòåëåé ìîæåò áûòü ðåàëèçîâàíà ïåðåäàòî÷-
íàÿ ôóíêöèÿ Í(ð) äîñòàòî÷íî îáùåãî âèäà.

367
14.4. Óñòîé÷èâîñòü öåïè ñ îáðàòíîé ñâÿçüþ
Ââåäåì ïîíÿòèÿ óñòîé÷èâîé è íåóñòîé÷èâîé öåïè. Öåïü íàçû-
âàåòñÿ óñòîé÷èâîé, åñëè ñâîáîäíûå êîëåáàíèÿ ñ òå÷åíèåì âðåìåíè
ñòðåìÿòñÿ ê íóëþ.  ïðîòèâíîì ñëó÷àå öåïü íàçûâàåòñÿ íåóñòîé-
÷èâîé. Èç òåîðèè ïåðåõîäíûõ ïðîöåññîâ (ãë. 6, 7) ñëåäóåò, ÷òî
öåïü ÿâëÿåòñÿ óñòîé÷èâîé, åñëè êîðíè õàðàêòåðèñòè÷åñêîãî óðàâ-
íåíèÿ ëåæàò â ëåâîé ïîëóïëîñêîñòè êîìïëåêñíîé ïåðåìåííîé ð.
Åñëè êîðíè òàêîãî óðàâíåíèÿ ëåæàò â ïðàâîé ïîëóïëîñêîñòè, òî
öåïü ÿâëÿåòñÿ íåóñòîé÷èâîé, ò. å. îíà íàõîäèòñÿ â ðåæèìå ñàìî-
âîçáóæäåíèÿ. Òàêèì îáðàçîì, äëÿ îïðåäåëåíèÿ óñëîâèé óñòîé÷è-
âîñòè öåïè äîñòàòî÷íî íàéòè õàðàêòåðèñòè÷åñêîå óðàâíåíèå è åãî
êîðíè. Êàê âèäèì, óñëîâèÿ óñòîé÷èâîñòè ìîæíî îïðåäåëèòü è íå
ââîäÿ ïîíÿòèå îáðàòíîé ñâÿçè. Îäíàêî çäåñü âîçíèêàåò ðÿä ïðî-
áëåì. Äåëî â òîì, ÷òî âûâîä õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ è îï-
ðåäåëåíèå åãî êîðíåé ÿâëÿþòñÿ ãðîìîçäêîé ïðîöåäóðîé îñîáåííî
äëÿ öåïåé âûñîêîãî ïîðÿäêà. Ââåäåíèå ïîíÿòèÿ îáðàòíîé ñâÿçè îá-
ëåã÷àåò ïîëó÷åíèå õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ èëè äàæå äàåò
âîçìîæíîñòü îáîéòèñü áåç íåãî. Êðàéíå âàæíî è òî, ÷òî ïîíÿòèå
îáðàòíîé ñâÿçè àäåêâàòíî ôèçè÷åñêèì ïðîöåññàì, âîçíèêàþùèì â
öåïè, ïîýòîìó îíè ñòàíîâÿòñÿ áîëåå íàãëÿäíûìè. Ãëóáîêîå ïîíè-
ìàíèå ôèçè÷åñêèõ ïðîöåññîâ îáëåã÷àåò ðàáîòó ïî ñîçäàíèþ àâòî-
ãåíåðàòîðîâ, óñèëèòåëåé è ò. ä.
Ðàññìîòðèì öåïü (ñì. ðèñ. 14.2) è âûâåäåì åå õàðàêòåðèñòè÷å-
ñêîå óðàâíåíèå. Ïóñòü u
âõ
(t) = 0 è, çíà÷èò, U
âõ
(ð) = 0. Òîãäà èç
(14.2) ñëåäóåò:
(
)
(
)
(
)
âûõocó
10.
UpHpHp
-×=
éù
ëû
(14.20)
Çäåñü U
âûõ
(ð) ¹ 0 (â ïðîòèâíîì ñëó÷àå öåïü íåëüçÿ ñ÷èòàòü âîçáó-
æäåííîé) è ïîýòîìó ðàâåíñòâî (14.20) âûïîëíÿåòñÿ ïðè óñëîâèè
(
)
(
)
oc ó
10.
HpHp
-=
(14.21)
Åñëè çàïèñàòü ïåðåäàòî÷íóþ ôóíêöèþ îñíîâíîé öåïè â âèäå (7.41):
(
)
(
)
(
)
ó
11
Hpwpvp
= , à öåïè ÎÑ $
(
)
(
)
(
)
oc22
Hpwpvp
=
, òî
óðàâíåíèå (14.11) ïåðåïèøåòñÿ ñëåäóþùèì îáðàçîì:
(
)
(
)
(
)
(
)
( ) ( )
1212
12
0.
vpvpwpwp
vpvp
-
=
Ýòî ðàâåíñòâî âûïîëíÿåòñÿ ïðè
(
)
(
)
(
)
(
)
1212
0.
vpvpwpwp
-=
(14.22)
Âûðàæåíèå â ëåâîé ÷àñòè ýòîãî ðàâåíñòâà ÿâëÿåòñÿ ïîëèíîìîì,
ïîýòîìó (14.22) ìîæíî çàïèñàòü â îáùåì âèäå:
1
110
0.
mm
mm
bpbpbpb
-
-
++++=
K
(14.23)
368
Ýòî è åñòü õàðàêòåðèñòè÷åñêîå óðàâíåíèå öåïè.
Çàìåòèì åùå ðàç, ÷òî òî÷íî òàêîå æå óðàâíåíèå ìû áû ïîëó÷è-
ëè, ñîñòàâëÿÿ äèôôåðåíöèàëüíîå óðàâíåíèå ïî çàêîíàì Êèðõãîôà,
êàê ìû ýòî äåëàëè ïðè èçó÷åíèè ïåðåõîäíûõ ïðîöåññîâ.
Êîðíè óðàâíåíèÿ (14.23) â îáùåì ñëó÷àå ÿâëÿþòñÿ êîìïëåêñ-
íûìè âåëè÷èíàìè
12
,,,,,,
m
k
pppp
KK
ãäå p
k
= a
k
+ jw
k
. Çíàÿ êîðíè õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ,
ìîæíî çàïèñàòü âûõîäíîå íàïðÿæåíèå (ñì. § 6.2):
( )
12
âûõ12
.
m
pt
ptpt
m
utAeAeAe=+++
K
(14.24)
×òîáû íàïðÿæåíèå u
âûõ
(t) íå âîçðàñòàëî áåçãðàíè÷íî, âñåì
êîðíÿì p
1
, p
2
, ... , p
m
õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ íåîáõîäèìî
èìåòü îòðèöàòåëüíûå âåùåñòâåííûå ÷àñòè, ò. å. êîðíè äîëæíû ðàñ-
ïîëàãàòüñÿ â ëåâîé ïîëóïëîñêîñòè êîìïëåêñíîé ïåðåìåííîé ð =
= a + jw. Öåïü ñ ÎÑ, îáëàäàþùàÿ òàêèìè ñâîéñòâàìè, íàçûâàåòñÿ
àáñîëþòíî óñòîé÷èâîé.
Ïðè èññëåäîâàíèè öåïåé ñ îáðàòíîé ñâÿçüþ ìîãóò âîçíèêàòü äâå
ïðîáëåìû. Åñëè ïðîåêòèðóåìàÿ öåïü äîëæíà áûòü óñòîé÷èâîé, òî
íåîáõîäèìî ðàñïîëàãàòü êðèòåðèåì, êîòîðûé ïî âèäó ôóíêöèé
Í
ó
(ð) è Í
îñ
(ð) ïîçâîëÿë áû ñóäèòü îá îòñóòñòâèè êîðíåé õà-
ðàêòåðèñòè÷åñêîãî óðàâíåíèÿ â ïðàâîé ïîëóïëîñêîñòè ð. Åñëè îá-
ðàòíàÿ ñâÿçü èñïîëüçóåòñÿ äëÿ ñîçäàíèÿ íåóñòîé÷èâîé àâòîêî-
ëåáàòåëüíîé öåïè, òî ñëåäóåò óáåäèòüñÿ, ÷òî êîðíè óðàâíåíèÿ
(14.23) ðàñïîëîæåíû, íàîáîðîò, â ïðàâîé ïîëóïëîñêîñòè. Ïðè ýòîì
íåîáõîäèìî èìåòü òàêîå ðàñïîëîæåíèå êîðíåé, ïðè êîòîðîì ñàìî-
âîçáóæäåíèå ïðîèñõîäèëî áû íà òðåáóåìîé ÷àñòîòå.
Ðàññìîòðèì êðèòåðèè óñòîé÷èâîñòè öåïè ñ îáðàòíîé ñâÿçüþ.
Êðèòåðèé óñòîé÷èâîñòè Ðàóñà $ Ãóðâèöà. Îí îòíîñèòñÿ ê àë-
ãåáðàè÷åñêèì êðèòåðèÿì óñòîé÷èâîñòè è ïîçâîëÿåò ïî çíà÷åíèÿì
êîýôôèöèåíòîâ b
ò
, b
ò$1
, ..., b
0
õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ
(14.23), áåç îïðåäåëåíèÿ åãî êîðíåé, óçíàòü ÿâëÿåòñÿ ëè èññëåäóå-
ìàÿ öåïü óñòîé÷èâîé.
Êðèòåðèé ôîðìóëèðóåòñÿ ñëåäóþùèì îáðàçîì: öåïü ñ îá-
ðàòíîé ñâÿçüþ ÿâëÿåòñÿ óñòîé÷èâîé, åñëè ïîëèíîì õàðàêòå-
ðèñòè÷åñêîãî óðàâíåíèÿ, ÿâëÿåòñÿ ïîëèíîìîì Ãóðâèöà. Ïðè
ýòîì èñïîëüçóåòñÿ îñíîâíîå ñâîéñòâî ïîëèíîìà Ãóðâèöà: âñå åãî
êîðíè íàõîäÿòñÿ â ëåâîé ïîëóïëîñêîñòè êîìïëåêñíîé ïåðåìåí-
íîé ð.
Äëÿ òîãî, ÷òîáû ìíîãî÷ëåí
1
110
mm
mm
bpbpbpb
-
-
++++
K
ÿâ-
ëÿëñÿ ïîëèíîìîì Ãóðâèöà, íåîáõîäèìî è äîñòàòî÷íî, ÷òîáû áûëè
ïîëîæèòåëüíûìè îïðåäåëèòåëü Ðàóñà%Ãóðâèöà:

369
135
24
13
1
2
0
0
0
00
;
00
..............
000
mmm
mmm
mm
n
mm
bbb
bbb
bb
D
bb
b
---
--
--
-
-
=
L
L
L
L
L
è âñå ãëàâíûå ìèíîðû ýòîãî îïðåäåëèòåëÿ.
Ïðè ñîñòàâëåíèè îïðåäåëèòåëÿ Ãóðâèöà ìîæíî ðóêîâîäñòâî-
âàòüñÿ ñëåäóþùèì ïðàâèëîì. Â ïåðâîé ñòðîêå çàïèñûâàþòñÿ êî-
ýôôèöèåíòû ïîëèíîìà Ãóðâèöà ÷åðåç îäèí, íà÷èíàÿ ñî âòîðîãî. Âî
âòîðîé ñòðîêå çàïèñûâàþòñÿ êîýôôèöèåíòû ïîëèíîìà ÷åðåç îäèí,
íà÷èíàÿ ñ ïåðâîãî. Âòîðàÿ ïàðà ñòðîê ôîðìèðóåòñÿ ïóòåì ñìåùå-
íèÿ ïåðâîé ïàðû ñòðîê íà îäíó ïîçèöèþ. Òðåòüÿ ïàðà % ñìåùåíè-
åì âòîðîé ïàðû ñòðîê åùå íà îäíó âïðàâî è ò. ä.
Ïðèìåð. Ïðîâåðèì ñ ïîìîùüþ êðèòåðèÿ Ðàóñà%Ãóðâèöà óñòîé÷èâîñòü öå-
ïè ñ îáðàòíîé ñâÿçüþ, õàðàêòåðèñòè÷åñêîå óðàâíåíèå êîòîðîé èìååò âèä
432
34620.
pppp
++++=
1. Ñîñòàâëÿåì îïðåäåëèòåëü Ðàóñà%Ãóðâèöà
3
3600
1420
.
0360
0142
D =
Ãëàâíûå ìèíîðû ïîëó÷àåì âû÷åðêèâàíèåì ïðàâîãî ñòîëáöà è íèæíåé ñòðîêè
èç îïðåäåëèòåëÿ èëè ïðåäûäóùåãî ìèíîðà:
210
360
36
,,.
142
3
14
036
DDD===
2. Âû÷èñëÿåì îïðåäåëèòåëü Ðàóñà%Ãóðâèöà è åãî ãëàâíûå ìèíîðû. Ðàñ÷åò
óäîáíî ïðîâîäèòü â ñëåäóþùåì ïîðÿäêå:
01
36
3,34616,
3
14
DD
====×-×=
( ) ( )
3332
21
360
36
6121662918,
142
03
036
DD
++
==-+-=×-×=
( )
44
32
3600
1420
2121836.
0360
0142
DD
+
==-=×=
Îïðåäåëèòåëü Ðàóñà%Ãóðâèöà è åãî ãëàâíûå ìèíîðû ïîëîæèòåëüíû. Òàêèì
îáðàçîì, öåïü ñ ÎÑ óñòîé÷èâà.

370
Êðèòåðèé óñòîé÷èâîñòè Íàéêâèñòà. Êðèòåðèé Íàéêâèñòà ïî-
çâîëÿåò ñóäèòü îá óñòîé÷èâîñòè öåïè ñ îáðàòíîé ñâÿçüþ ïî ñâîéñò-
âàì ðàçîìêíóòîé öåïè (ðèñ. 14.3, à).
Ïåðåäàòî÷íàÿ ôóíêöèÿ ðàçîìêíóòîé öåïè, èëè ïåòëåâîå óñèëå-
íèå,
(
)
(
)
(
)
p ó
oc
HjHjHj
w=w×w
âõîäèò â õàðàêòåðèñòè÷åñêîå
óðàâíåíèå (14.21):
(
)
p
10.
Hj
-w=
(14.25)
Åñëè íàéäåòñÿ òàêàÿ ÷àñòîòà w, äëÿ êîòîðîé êîíåö âåêòîðà
H
ð
(jw) ïîïàäàåò â òî÷êó ñ êîîðäèíàòàìè (1,j0), òî ýòî áóäåò îç-
íà÷àòü, ÷òî âûïîëíÿåòñÿ óñëîâèå (14.25), ò. å. íà ýòîé ÷àñòîòå â
öåïè ïðîèçîéäåò ñàìîâîçáóæäåíèå. Çíà÷èò, ïî ãîäîãðàôó ìîæíî
îïðåäåëèòü, óñòîé÷èâà öåïü èëè íåò. Äëÿ ýòîãî èñïîëüçóåòñÿ êðè-
òåðèé Íàéêâèñòà, êîòîðûé ôîðìóëèðóåòñÿ ñëåäóþùèì îáðàçîì:
åñëè ãîäîãðàô ïåðåäàòî÷íîé ôóíêöèè ðàçîìêíóòîé öåïè íå îõ-
âàòûâàåò òî÷êó ñ êîîðäèíàòàìè (1, j0), òî ïðè çàìêíóòîé
öåïè îáðàòíîé ñâÿçè öåïü ÿâëÿåòñÿ óñòîé÷èâîé.  òîì ñëó÷àå,
êîãäà ãîäîãðàô H
ð
(w) îõâàòûâàåò òî÷êó (1, j0), öåïü íåóñòîé÷è-
âà. Íà ðèñ. 14.4 ïîêàçàíû ãîäîãðàôû òðåõ öåïåé ñ ïîëîæèòåëü-
íîé îáðàòíîé ñâÿçüþ (öèôðà 1 ñîîòâåòñòâóåò ãîäîãðàôó óñòîé÷è-
âîé öåïè).
Ïîëüçóÿñü êðèòåðèåì Íàéêâèñòà, ëåãêî ïîëó÷èòü óñëîâèÿ ñàìî-
âîçáóæäåíèÿ öåïè ñ ÎÑ. Çàïèøåì âûðàæåíèå äëÿ H
ð
(jw) â âèäå
( ) ( ) ( )
(
)
(
)
óoc
p óoc
,
j
HjHjHje
jw+jw
éù
ëû
w=w×w
ãäå
(
)
(
)
ó
oc
,
HjHj
ww
$ ìîäóëè ïåðåäàòî÷íûõ ôóíêöèé;
(
)
ó
jw
,
(
)
oc
jw
$ ôàçîâûå ñäâèãè ñîîòâåòñòâåííî â îñíîâíîì ýëåìåíòå è â
öåïè ÎÑ.
Óñëîâèÿ ïåðåñå÷åíèÿ ãîäîãðàôîì îñè àáñöèññ Re[H
ð
(jw)] ïðè
|H
ð
(jw)|
1 ìîæíî çàïèñàòü â âèäå äâóõ óñëîâèé:
1) óñëîâèå (óðàâíåíèå) áàëàíñà ôàç
(
)
(
)
ó
oc
2
n
jw+jw=p
, ãäå
ï = 0, 1, 2,...;
2) àìïëèòóäíîå óñëîâèå
(
)
(
)
(
)
(
)
óocóoc
1,
èëè1.
HjHjHHwwww
Âûïîëíåíèå íåðàâåíñòâà ñîîòâåòñòâóåò ðåæèìó âîçíèêíîâåíèÿ
êîëåáàíèé ñ íàðàñòàþùåé àìïëèòóäîé, ÷òî õàðàêòåðíî äëÿ íà-
÷àëüíîãî ýòàïà ñàìîâîçáóæäåíèÿ. Âûïîëíåíèå ðàâåíñòâà H
ó
(w)´
´H
îñ
(w) = 1 ñîîòâåòñòâóåò ðåæèìó ãåíåðàöèè ãàðìîíè÷åñêîãî íà-
ïðÿæåíèÿ íà ÷àñòîòå w ñ ïîñòîÿííîé àìïëèòóäîé è íîñèò íàçâàíèå
áàëàíñà àìïëèòóä.
Êàê áóäåò ïîêàçàíî íèæå, óðàâíåíèå áàëàíñà ôàç ïîçâîëÿåò îï-
ðåäåëèòü ÷àñòîòó, íà êîòîðîé ïðîèñõîäèò ñàìîâîçáóæäåíèå öåïè ñ
ÎÑ, à óðàâíåíèå áàëàíñà àìïëèòóä äàåò âîçìîæíîñòü îïðåäåëèòü
