Бакалов В.П. Основы теории цепей. 3-е издание

Подождите немного. Документ загружается.

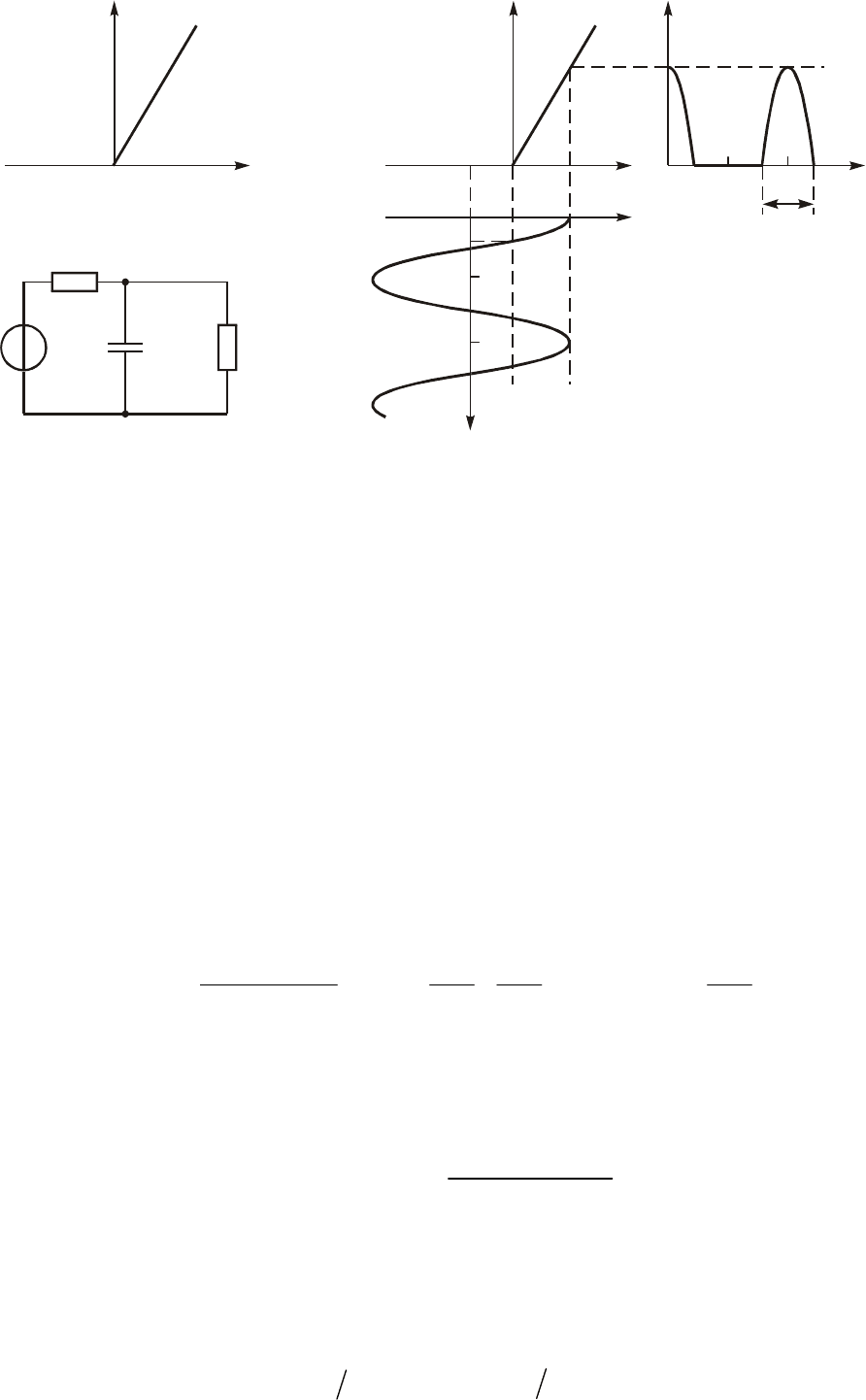
281

äèîäà èìååò âèä, ïîêàçàííûé íà ðèñ. 11.19. Ñîïðîòèâëåíèå äèîäà

ïðè u

> 0 ñ ó÷åòîì ðåçèñòèâíîãî âíóòðåííåãî ñîïðîòèâëåíèÿ ãåíå-

ðàòîðà, îáîçíà÷èì ÷åðåç R

. Ïîëîæèì, äàëåå, ÷òî ôëþêòóàöèè íà-

ïðÿæåíèÿ îòíîñèòåëüíî åãî ïîñòîÿííîé ñîñòàâëÿþùåé U

ïðåíåá-

ðåæèìî ìàëû, ò.å. áóäåì ñ÷èòàòü, ÷òî u

(t) @ U

= const. O äîïóñ-

òèìîñòè ýòîãî ïðåäïîëîæåíèÿ, êîòîðîå ïîòðåáóåòñÿ âûïîëíÿòü íà

ïðàêòèêå, ìîæíî ñóäèòü ïî ïðèâåäåííîìó âûøå ïðèìåðó.

Ïðè óêàçàííûõ äîïóùåíèÿõ òîê ÷åðåç äèîä â öåïè, ñõåìà êîòî-

ðîé äëÿ u

(t) = U

ïðèâåäåíà íà ðèñ. 11.20, ïðåäñòàâëÿåò ñîáîé

ïåðèîäè÷åñêóþ ïîñëåäîâàòåëüíîñòü èìïóëüñîâ, ïîäîáíóþ ïîêàçàí-

íîé íà ðèñ. 11.10, à.

Ãðàôè÷åñêèå ïîñòðîåíèÿ, èëëþñòðèðóþùèå ïðîöåññû â àíàëè-

çèðóåìîé öåïè, ïîêàçàíû íà ðèñ. 11.21. Èç íèõ ñëåäóåò, ÷òî

( )

äää

cos è

11cos.

mmm

max

UUUUU

RURR

æö

==-=-q

ç÷

èø

Ýòîìó çíà÷åíèþ ìàêñèìóìà òîêà ñîîòâåòñòâóåò ñîãëàñíî (11.10, à)

ïîñòîÿííàÿ ñîñòàâëÿþùàÿ òîêà

sincos

max

q-qq

D=a=

ïðîòåêàþùåãî ÷åðåç äèîä è íàãðóçêó.

Çàìåíÿÿ â ýòîì âûðàæåíèè DI

íà U

è ó÷èòûâàÿ, ÷òî

cos

, íàõîäèì çàâèñèìîñòü ìåæäó óãëîì îòñå÷êè è ñîïðî-

òèâëåíèåì äèîäà è íàãðóçêè:

(

)

ä í

tg.

=q-qp

0,5

max

0,5

()=()

tut

()

Ðèñ. 11.19

Ðèñ. 11.20

Ðèñ. 11.21

282

Ðåøèâ ýòî òðàíñöåíäåíòíîå óðàâíåíèå, îïðåäåëÿåì íåèçâåñòíûé

ïîêà óãîë îòñå÷êè q, êàê ôóíêöèþ îòíîøåíèÿ ñîïðîòèâëåíèé

, à çàòåì è âåëè÷èíó âûïðÿìëåííîãî ïîñòîÿííîãî íàïðÿæå-

íèÿ

cos

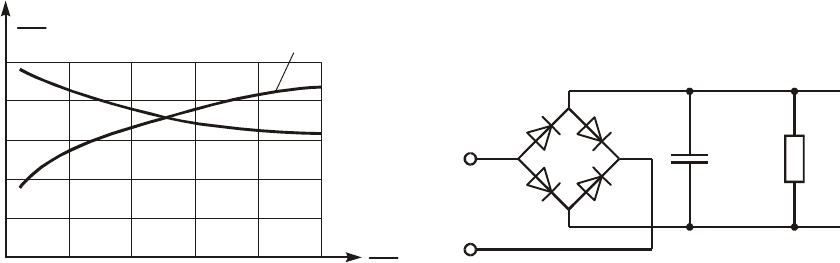
Íà ðèñ. 11.22 ïðèâåäåí â îòíîñèòåëüíûõ åäèíèöàõ ãðàôèê çàâè-

ñèìîñòè âûïðÿìëåííîãî ïîñòîÿííîãî íàïðÿæåíèÿ U

îò ñîïðî-

òèâëåíèÿ äèîäà R

. Äàííûå ðèñóíêè ïîêàçûâàþò, ÷òî ïðè

)

1 âåëè÷èíà ïîñòîÿííîãî íàïðÿæåíèÿ áëèçêà ê àìïëè-

òóäå âûïðÿìëÿåìîãî ãàðìîíè÷åñêîãî íàïðÿæåíèÿ è óáûâàåò ïðè

ïðî÷èõ ðàâíûõ óñëîâèÿõ ñ óâåëè÷åíèåì ñîïðîòèâëåíèÿ äèîäà. ×à-

ùå âñåãî (R

)  0,1, êîãäà U

 0,65U

, èíà÷å ÊÏÄ âûïðÿìè-

òåëÿ ñòàíîâèòñÿ íåäîïóñòèìî ìàëûì. Íà òîì æå ðèñóíêå ïîêàçàí

ãðàôèê çàâèñèìîñòè óãëà îòñå÷êè â ðàäèàíàõ îò òîãî æå îòíîøåíèÿ

. Ïðè (R

) < 0,1 óãîë îòñå÷êè íå ïðåâûøàåò 0,87 ðàä,

ò. å. 50°, è óáûâàåò ñ óìåíüøåíèåì îòíîøåíèÿ (R

Ðàññìîòðåííûå ïðîñòåéøèå âûïðÿìèòåëè íàçûâàþòñÿ îäíîïîëó-

ïåðèîäíûìè, ïîñêîëüêó ó íèõ ïðè ôîðìèðîâàíèè âûïðÿìëåííîãî

íàïðÿæåíèÿ èñïîëüçóåòñÿ ýíåðãèÿ òîëüêî îäíîãî èç êàæäîé ïàðû

ïîëóïåðèîäîâ âûïðÿìëÿåìîãî ãàðìîíè÷åñêîãî íàïðÿæåíèÿ, à, òî÷-

íåå, åãî ÷àñòè.

Ñõåìà äâóõïîëóïåðèîäíîãî âûïðÿìèòåëÿ ìîñòîâîãî òèïà èçî-

áðàæåíà íà ðèñ. 11.23. Çäåñü çà ñ÷åò ïîî÷åðåäíîãî îòêðûòèÿ äèî-

äîâ, ïîìå÷åííûõ íà ðèñóíêå ÷åòíûìè è íå÷åòíûìè èíäåêñàìè, äîñ-

òèãàåòñÿ ïîñòîÿíñòâî çíàêà òîêà â íàãðóçêå âûïðÿìèòåëÿ äëÿ îáîèõ

ïîëóïåðèîäîâ âûïðÿìëÿåìîãî íàïðÿæåíèÿ. Èìåííî äâóõïîëóïåðè-

îäíûå âûïðÿìèòåëè íàøëè ïðåèìóùåñòâåííîå ïðèìåíåíèå äëÿ âû-

ïðÿìëåíèÿ îäíîôàçíîãî ãàðìîíè÷åñêîãî íàïðÿæåíèÿ. Êà÷åñòâåí-

íûå è êîëè÷åñòâåííûå îöåíêè ïðîöåññîâ â äâóõïîëóïåðèîäíûõ âû-

ïðÿìèòåëÿõ ìîæíî ïîëó÷èòü ïðÿìûì îáîáùåíèåì òàêîâûõ â âû-

ïðÿìèòåëÿõ îäíîïîëóïåðèîäíûõ.

Äëÿ áîëåå ïîëíîãî ïîäàâëåíèÿ ãàðìîíèê, åñëè â ýòîì âîçíèêàåò

íåîáõîäèìîñòü, â âûïðÿìèòåëü ââîäÿòñÿ â äîïîëíåíèå ê êîíäåíñà-

òîðó îäèí èëè äâà ðåàêòèâíûõ ýëåìåíòà, îáðàçóþùèå ôèëüòð íèæ-

íèõ ÷àñòîò ñ íåîáõîäèìûì îñëàáëåíèåì íà ÷àñòîòàõ ãàðìîíèê. Çà-

0,02

0,04

0,06

0,08

0,1

0,2

0,4

0,6

0,8

()

Ðèñ. 11.22 Ðèñ. 11.23

283

äà÷à ôèëüòðàöèè ãàðìîíèê äâóõïîëóïåðèîäíîãî âûïðÿìèòåëÿ îá-

ëåã÷àåòñÿ òåì, ÷òî ó íåãî àìïëèòóäà ïóëüñàöèé âûïðÿìëåííîãî íà-

ïðÿæåíèÿ âäâîå ìåíüøå, à èõ ÷àñòîòà âäâîå âûøå, ÷åì ó âûïðÿìè-

òåëÿ îäíîïîëóïåðèîäíîãî ïðè ïðî÷èõ ðàçíûõ óñëîâèÿõ. Â áûòîâîé

ðàäèîýëåêòðîííîé àïïàðàòóðå âìåñòî ôèëüòðà â äîïîëíåíèå ê êîí-

äåíñàòîðó ñóùåñòâåííîå ïîäàâëåíèå ãàðìîíèê îñóùåñòâëÿåò âêëþ-

÷åííûé íà âûõîäå âûïðÿìèòåëÿ ñòàáèëèçàòîð íàïðÿæåíèÿ $ óñò-

ðîéñòâî äëÿ ïîääåðæàíèÿ ïîñòîÿíñòâà íàïðÿæåíèÿ íà åãî âûõîäå

ïðè èçìåíåíèè ñîïðîòèâëåíèÿ åãî íàãðóçêè.

11.6. Îãðàíè÷åíèå ìãíîâåííûõ çíà÷åíèé

ãàðìîíè÷åñêèõ êîëåáàíèé

Íåëèíåéíûé ÷åòûðåõïîëþñíèê, ïðåäíàçíà÷åííûé äëÿ îãðàíè÷å-

íèÿ ìãíîâåííûõ íàïðÿæåíèé ñèãíàëà, íàçûâàåòñÿ îãðàíè÷èòåëåì.

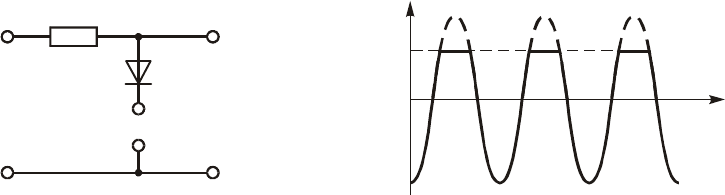
Ñõåìà ïðîñòåéøåãî îãðàíè÷èòåëÿ ñ îãðàíè÷åíèåì ñâåðõó ïðèâå-

äåíà íà ðèñ. 11.24, à. Â îãðàíè÷èòåëü âõîäÿò ëèíåéíûé ðåçèñòîð ñ

ñîïðîòèâëåíèåì R, âûïðÿìèòåëüíûé äèîä è ãåíåðàòîð ïîñòîÿííîãî

íàïðÿæåíèÿ ñ çàäàþùèì ïîðîãîâûì íàïðÿæåíèåì U

. Íà ïåðâîì

ýòàïå àíàëèçà ïðîöåññîâ â ðàññìàòðèâàåìîì îãðàíè÷èòåëå áóäåì

ñ÷èòàòü, âî-ïåðâûõ, ÷òî äèîä èäåàëåí, ò. å. åãî ñîïðîòèâëåíèå èëè

áåñêîíå÷íî âåëèêî, åñëè u

< 0, èëè ðàâíî íóëþ, åñëè u

> 0, è âî-

âòîðûõ, ÷òî âíóòðåííåå ñîïðîòèâëåíèå ãåíåðàòîðà ïîñòîÿííîãî íà-

ïðÿæåíèÿ ðàâíî íóëþ.

Åñëè ïðè óêàçàííûõ ïðåäïîëîæåíèÿõ íàïðÿæåíèå íà çàæèìàõ

äèîäà áóäåò îòðèöàòåëüíûì, ò. å. êîãäà u

âõ

(t) < U

, äèîä áóäåò

«çàêðûò» è íàïðÿæåíèå íà âûõîäå îãðàíè÷èòåëÿ áóäåò ðàâíî íà-

ïðÿæåíèþ íà åãî âõîäå, ò. å. u

âûõ

(t) = u

âõ

(t). Åñëè æå u

âõ

(t) > U

äèîä «îòêðûâàåòñÿ», åãî ñîïðîòèâëåíèå ñòàíîâèòñÿ ðàâíûì íóëþ.

Òåì ñàìûì èñòî÷íèê ïîñòîÿííîãî íàïðÿæåíèÿ ïîäêëþ÷àåòñÿ ê âû-

õîäó îãðàíè÷èòåëÿ è íàïðÿæåíèå íà âûõîäå îãðàíè÷èòåëÿ áóäåò

ðàâíî çàäàþùåìó íàïðÿæåíèþ èñòî÷íèêà U

íà ïðîòÿæåíèè âñåãî

âðåìåíè ïîêà u

âõ

> U

. Èòàê:

()

(

)

(

)

()

{

âõ âõï

âûõ

ï âõï

ïðè,

ïðè.

ututU

UutU

âõ

()

âûõ

()

)

Ðèñ. 11.24

284

Ñîîòâåòñòâóþùàÿ ãðàôè÷åñêàÿ èëëþñòðàöèÿ ïðèâåäåíà íà

ðèñ. 10.24, á äëÿ âîçäåéñòâèÿ â âèäå ãàðìîíè÷åñêîãî êîëåáàíèÿ

(

)

(

)

âõ

cos

utUt

=w+j

. Øòðèõîâîé ëèíèåé íà ðèñóíêå ïîêàçàíû

«îòñå÷åííûå» îãðàíè÷èòåëåì ó÷àñòêè âõîäíîãî êîëåáàíèÿ.

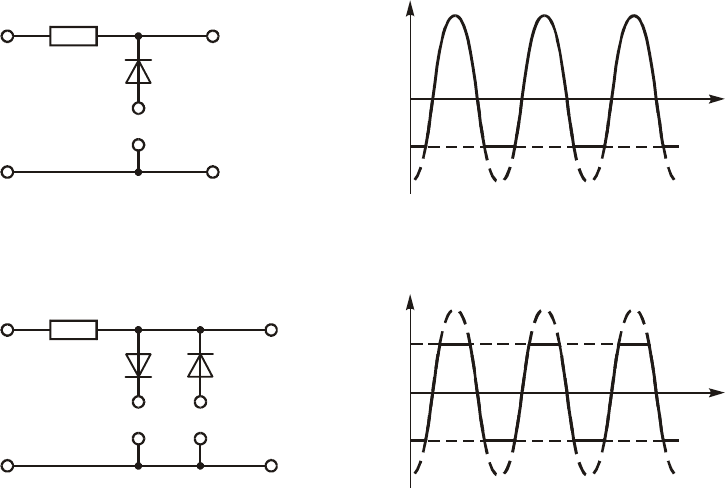
Íà ðèñ. 10.25, à èçîáðàæåíà ñõåìà îãðàíè÷èòåëÿ ñ îãðàíè÷åíè-

åì ñíèçó. Àíàëîãè÷íûå ðàññóæäåíèÿ ïîêàçûâàþò, ÷òî ó òàêîãî îã-

ðàíè÷èòåëÿ ïðè òåõ æå, ÷òî è âûøå, äîïóùåíèÿõ:

()

(

)

(

)

()

{

âõ âõï

âûõ

ï âõï

ïðè,

ïðè.

ututU

UutU

-<-

Ãðàôèê íàïðÿæåíèÿ íà âûõîäå îãðàíè÷èòåëÿ ñ îãðàíè÷åíèåì

ñíèçó äëÿ òîãî æå, ãàðìîíè÷åñêîãî, âîçäåéñòâèÿ èçîáðàæåí íà

ðèñ. 10.25, á.

Íàêîíåö, íà ðèñ. 10.26, à ïðèâåäåíà ñõåìà îãðàíè÷èòåëÿ ñ äâóõ-

ñòîðîííèì îãðàíè÷åíèåì, ó êîòîðîãî äëÿ ïðèíÿòûõ äîïóùåíèé

()

(

)

() ()

()

ï1 âõï1

âûõ âõï2 âõï1

ï2 âõï2

ïðè,

ïðè.

UutU

ututUutU

UutU

=-<<

-<-

Îáû÷íî îãðàíè÷èòåëè ñ äâóõñòîðîííèì îãðàíè÷åíèåì èìåþò

êàê ñèììåòðè÷íûå, òàê è àñèììåòðè÷íûå ïðåäåëû îãðàíè÷åíèé.

Íàïðÿæåíèå íà âûõîäå îãðàíè÷èòåëÿ ñ ñèììåòðè÷íûìè ïðåäå-

ëàìè îãðàíè÷åíèÿ, åñëè ê åãî âõîäó ïîäàåòñÿ ãàðìîíè÷åñêîå íàïðÿ-

æåíèå

(

)

(

)

cos

âõm

utUt

=w+j

, ïî ôîðìå áëèçêî ê ïåðèîäè÷åñêîé

ïîñëåäîâàòåëüíîñòè èìïóëüñîâ òðàïåöèåäàëüíîé ôîðìû è ÷åðåäóþ-

ùåéñÿ ïîëÿðíîñòè (ñì. ðèñ. 11.2). Ôîðìà èìïóëüñîâ ïðèáëèæàåòñÿ

ê ïðÿìîóãîëüíîé ïî ìåðå óñèëåíèÿ íåðàâåíñòâà U

> U

ï1

= U

ï2

âõ

()

âûõ

()

)

Ðèñ. 11.25

ï1

âõ

()

âûõ

-U

ï2

âûõ

()

)

ï1

ï2

Ðèñ. 11.26

285

Åñëè ðàññìàòðèâàåìóþ ïåðèîäè÷åñêóþ ïîñëåäîâàòåëüíîñòü èì-

ïóëüñîâ ïîäâåñòè ê óñòðîéñòâó, ìîäåëèðóþùåìó îïåðàöèþ äèôôå-

ðåíöèðîâàíèÿ, òî íàïðÿæåíèå íà åãî âûõîäå áóäåò ïðåäñòàâëÿòü

ñîáîé ïåðèîäè÷åñêóþ ïîñëåäîâàòåëüíîñòü êîðîòêèõ èìïóëüñîâ ÷å-

ðåäóþùåéñÿ ïîëÿðíîñòè. Ôîðìà êàæäîãî îòäåëüíîãî èìïóëüñà

áëèçêà ê ïðÿìîóãîëüíîé; åãî äëèòåëüíîñòü òåì ìåíüøå, à âûñîòà

òåì áîëüøå, ÷åì áîëüøå àìïëèòóäà ãàðìîíè÷åñêîãî êîëåáàíèÿ ïðå-

âûøàåò ïîðîã îãðàíè÷åíèÿ.

Â çàêëþ÷åíèå çàìåòèì, ÷òî çàäà÷ó àíàëèçà êîëåáàíèé â îãðàíè-

÷èòåëå ìîæíî ðåøàòü ñ ó÷åòîì ðåàëüíûõ õàðàêòåðèñòèê äèîäîâ è

êîíå÷íîãî âíóòðåííåãî ñîïðîòèâëåíèÿ ãåíåðàòîðîâ. Ïðè ýòîì êà÷å-

ñòâåííî êàðòèíà ïðîöåññîâ â îãðàíè÷èòåëå ïðàêòè÷åñêè ñîõðàíèòñÿ

áåç èçìåíåíèé ïî ñðàâíåíèþ ñ ðàññìîòðåííîé âûøå.

11.7. Âîçäåéñòâèå ñóììû ãàðìîíè÷åñêèõ êîëåáàíèé íà

íåëèíåéíûé ðåçèñòèâíûé ýëåìåíò

Ñïåêòðàëüíûé ñîñòàâ òîêà ïðè áèãàðìîíè÷åñêîì âîçäåéñòâèè.

Ïóñòü ê íåëèíåéíîìó ðåçèñòèâíîìó ýëåìåíòó ïîäâåäåíî áèãàðìî-

íè÷åñêîå âîçäåéñòâèå, ò. å. êîëåáàíèå â âèäå ñóììû äâóõ ãàðìîíè-

÷åñêèõ êîëåáàíèé ðàçíûõ ÷àñòîò è ïîñòîÿííîå íàïðÿæåíèå ñìåùå-

íèÿ U

(

)

(

)

0111222

coscos.

UUUtUt

=+w+j+w+j

Ïðåäïîëîæèì, ÷òî ÂÀÕ íåëèíåéíîãî ýëåìåíòà îïèñûâàåòñÿ ïî-

ëèíîìîì

()

( ) ( ) ( )

010200

itaanUanUanU=+-+-++-

Òîãäà òîê â öåïè ÍÝ ðàâåí:

()

( ) ( )

[ ]

111222

coscos.

itaUtUt

=w+j+w+j

(11.13)

Äëÿ àíàëèçà ñïåêòðà òîêà àïïàðàò ðÿäîâ Ôóðüå çäåñü íå ïðèìå-

íèì, òàê êàê â îáùåì ñëó÷àå ôóíêöèÿ (11.13) íå ÿâëÿåòñÿ ïåðèî-

äè÷åñêîé. Ñëåäóåò, êàê è ïðè ãàðìîíè÷åñêîì âîçäåéñòâèè íà ÍÝ,

âîñïîëüçîâàòüñÿ ôîðìóëàìè ïðåîáðàçîâàíèÿ òðèãîíîìåòðè÷åñêèõ

ôóíêöèé. Ïðè ýòîì

äëÿ êâàäðàòè÷íîãî ÷ëåíà ñóììû (11.13)

()

( ) ( )

[ ]

22111222

coscos

itaUtUt

=w+j+w+j=

(

)

(

)

211222

coscos

aUtaUt

=w+j+w+j+

(

)

(

)

21211222

2coscos2

aUUttaU

+w+jw+j=+

( ) ( )

222

212

1122

cos22cos22

222

mmm

aUaUaU

++w+j+w+j+

286

(

)

2121212

cos

aUUt

w+w+j+j+

éù

ëû

(

)

2121212

cos;

aUUt+w-w+j-j

éù

ëû

äëÿ êóáè÷íîãî ÷ëåíà

( ) ( )

33111222

()coscos

itaUtUt

=w+j+w+j=

éù

ëû

()

3111

cos

aUUUt

æö

=+w+j+

ç÷

èø

()

3222

cos

aUUUt

æö

++w+j+

ç÷

èø

()()

311322

cos33cos33

atat

+w+j+w+j+

( )

321212

cos22

aUUt

+w+w+j+j+

éù

ëû

( )

321212

cos22

aUUt

+w-w+j-j+

éù

ëû

( )

311212

cos22

aUUt

+w+w+j+j+

éù

ëû

( )

311212

cos22

aUUt

+w-w+j-j

éù

ëû

è ò. ä.

Äîïóñòèì, ÷òî n = 3, ò. å., ÷òî âîëüò-àìïåðíàÿ õàðàêòåðèñòèêà

íåëèíåéíîãî ýëåìåíòà îïèñûâàåòñÿ ïîëèíîìîì òðåòüåé ñòåïåíè. Òî-

ãäà ïîëó÷åííûå âûøå âûðàæåíèÿ äëÿ i

(t) è i

(t) ïîêàçûâàþò, ÷òî

òîê â ýëåìåíòå êðîìå ëèíåéíîé ñîñòàâëÿþùåé ðåàêöèè i

(t) =

(

)

(

)

11111222

coscos

aUtaUt

=w+j+w+j

ñîäåðæèò òàêæå ïîñòî-

ÿííóþ ñîñòàâëÿþùóþ, ãàðìîíè÷åñêèå êîëåáàíèÿ ñ ÷àñòîòàì âîçäåé-

ñòâèÿ w

è w

è ãàðìîíèêè êîëåáàíèé ñ ÷àñòîòàìè 2w

, 2w

,3w

Ïåðå÷èñëåííûå ñîñòàâëÿþùèå ñïåêòðà õàðàêòåðíû è äëÿ âîç-

äåéñòâèÿ íà òîò æå ýëåìåíò äâóõ ãàðìîíè÷åñêèõ êîëåáàíèé ñ ÷àñòî-

òàìè w

è w

ïîðîçíü. Ïðè ñîâìåñòíîì æå èõ âîçäåéñòâèè â ñïåê-

òðå ðåàêöèè ïîÿâëÿþòñÿ êîëåáàíèÿ ñ ÷àñòîòàìè

± w

|, |2w

± w

| è | w

± 2w

Ñîîòâåòñòâóþùèå êîëåáàíèÿ íàçûâàþòñÿ êîìáèíàöèîííûìè, à

èõ ÷àñòîòû - êîìáèíàöèîííûìè ÷àñòîòàìè. Àìïëèòóäû êîìáèíà-

öèîííûõ êîëåáàíèé çàâèñÿò îò àìïëèòóä îáåèõ ñîñòàâëÿþùèõ áè-

ãàðìîíè÷åñêîãî âîçäåéñòâèÿ è â ðàññìàòðèâàåìîì ïðèìåðå äëÿ êî-

ëåáàíèé ñ ÷àñòîòàìè

± w

|, |2w

± w

| è | w

± 2w

Çíàê ìîäóëÿ â îáùåì ñëó÷àå íåîáõîäèì, òàê êàê ÷àñòîòà êîëåáàíèÿ íå ìîæåò áûòü îòðèöà-

òåëüíîé.

287

ïðîïîðöèîíàëüíû ñîîòâåòñòâåííî ïðîèçâåäåíèÿì

112

mmm

UUUU

Àíàëîãè÷íûå âûêëàäêè äëÿ îñòàëüíûõ ÷ëåíîâ ñóììû (11.13)

ïðèâîäÿò ê çàêëþ÷åíèþ, ÷òî ïðè áèãàðìîíè÷åñêîì âîçäåéñòâèè íà

íåëèíåéíûé ýëåìåíò ñ ïîëèíîìèàëüíîé âîëüò-àìïåðíîé õàðàêòåðè-

ñòèêîé ñïåêòð ðåàêöèè ñîäåðæèò ãàðìîíè÷åñêèå êîëåáàíèÿ ñ ÷àñòî-

òàìè

w=w±w

(11.14)

ãäå l = 0, 1, 2, ..., n; m = 0, 1, 2, ..., n, l + m  n.

Ñóììà l + m îïðåäåëÿåò ïîðÿäîê êîìáèíàöèîííîãî êîëåáàíèÿ ñ

÷àñòîòîé (11.14). Òàê, êîìáèíàöèîííûå êîëåáàíèÿ 4-ãî ïîðÿäêà $

ýòî êîëåáàíèå ñ ÷àñòîòàìè 4w

, |3w

± w

|, |2w

± 2w

|, |w

± 3w

| è

Êîìáèíàöèîííûå ÷àñòîòû ïðè âîçäåéñòâèè ñóììû ãàðìîíè÷å-

ñêèõ êîëåáàíèé. Â îáùåì ñëó÷àå âõîäíîå âîçäåéñòâèå ìîæíî ïðåä-

ñòàâèòü áåñêîíå÷íîé ñóììîé

()

( )

cos.

mkkk

utUUt

=+w+j

Â çàâèñèìîñòè îò ñòåïåíè n àïïðîêñèìèðóþùåãî ïîëèíîìà â

ñïåêòðå òîêà, ïðîòåêàþùåãî ÷åðåç íåëèíåéíûé ýëåìåíò, ïîÿâëÿþò-

ñÿ êîìáèíàöèîííûå ÷àñòîòû âèäà:

123

;;

lmsklmskn

w±w±w±w±+++++

KKK

„

l, m, s, k $ öåëûå ïîëîæèòåëüíûå ÷èñëà. Íàïðèìåð, ïðè âîçäåéñò-

âèè íà ÍÝ ñ ÂÀÕ â âèäå ïîëèíîìà âòîðîé ñòåïåíè ñóììû òðåõ

ãàðìîíè÷åñêèõ êîëåáàíèé â ñïåêòðå òîêà, ïîìèìî ïîñòîÿííîé ñî-

ñòàâëÿþùåé è ïåðâûõ äâóõ ãàðìîíèê êàæäîé ÷àñòîòû, ïðèñóòñòâó-

þò êîìáèíàöèîííûå ÷àñòîòû |w

± w

|; |w

± w

|; |w

± w

|. Ïðè àï-

ïðîêñèìàöèè ïîëèíîìîì òðåòüåé ñòåïåíè äîïîëíèòåëüíî ïîÿâëÿþò-

ñÿ òðåòüè ãàðìîíèêè ñ ÷àñòîòàìè 3w

, 3w

è êîëåáàíèÿ ñ êîì-

áèíàöèîííûìè ÷àñòîòàìè òèïà |w

± w

|, |2w

± w

|, |w

± 2w

è ò. ä.

11.8. Ïðåîáðàçîâàíèå ÷àñòîòû ãàðìîíè÷åñêîãî êîëåáàíèÿ

Ïðè ïåðåäà÷å ýëåêòðè÷åñêèõ ñèãíàëîâ íà ðàññòîÿíèå ÷àñòî òðåáó-

åòñÿ ïåðåíîñèòü ñïåêòð ñèãíàëà ââåðõ èëè âíèç ïî øêàëå ÷àñòîò. Òà-

êîé ïåðåíîñ ñïåêòðà íàçûâàåòñÿ ïðåîáðàçîâàíèåì ÷àñòîòû. Íåîá-

õîäèìîñòü â ïðåîáðàçîâàíèè ÷àñòîò âîçíèêàåò, íàïðèìåð, â ñëó÷àÿõ

åñëè ñïåêòð ñèãíàëà, êîòîðûé íóæíî ïåðåäàòü, ðàñïîëîæåí íà øêàëå

÷àñòîò çíà÷èòåëüíî íèæå ïîëîñû ïðîïóñêàíèÿ ñèñòåìû ïåðåäà÷è.

Â êà÷åñòâå ïðåîáðàçîâàòåëÿ ÷àñòîòû ìîæåò áûòü èñïîëüçîâàí

óñèëèòåëüíûé êàñêàä íà òðàíçèñòîðå ñ êîëåáàòåëüíûì êîíòóðîì

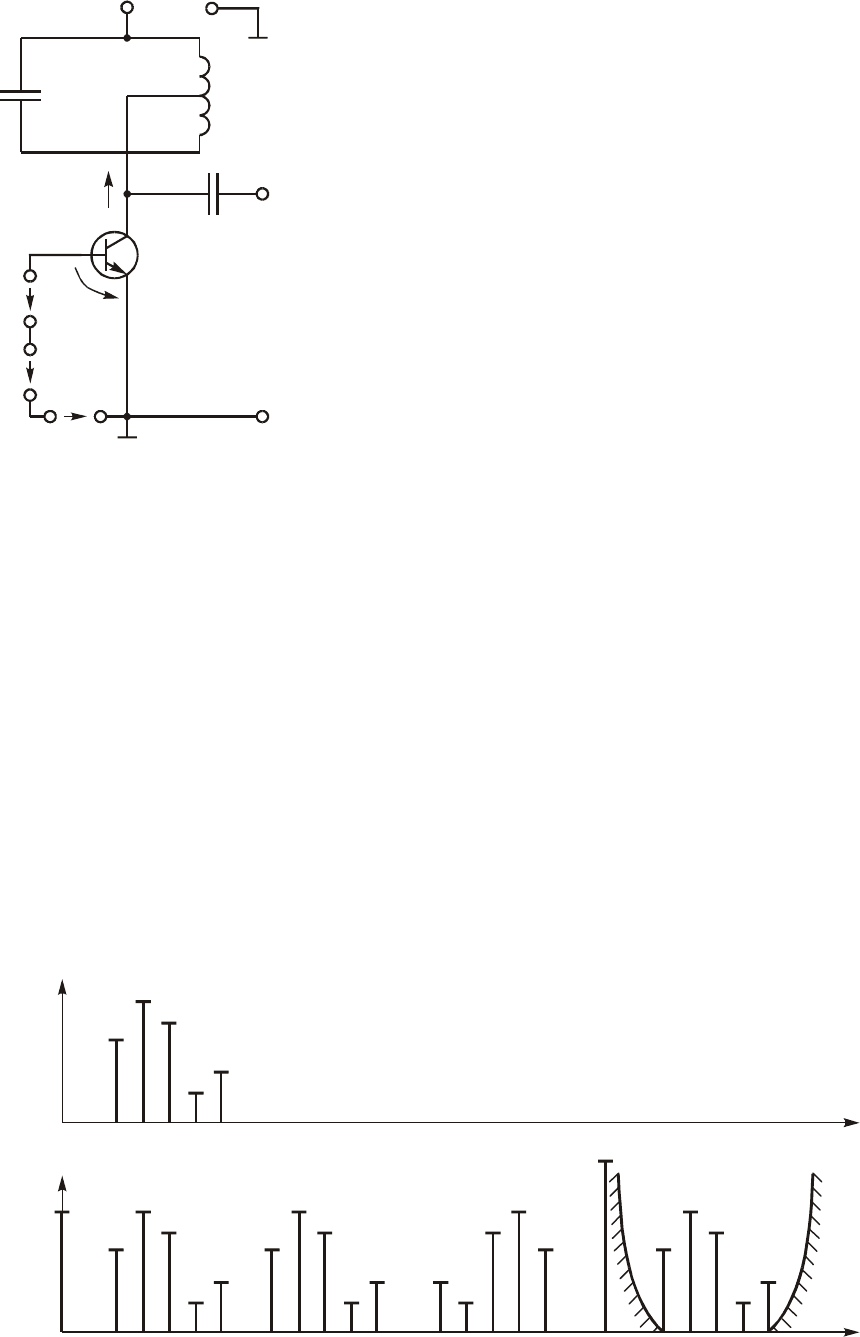
288

)

...

()

...

()

... w- W

w- W

...

w+ W

...

w+ W

Ðèñ. 11.28

ïèò

âûõ

()

ÁÝ

()

Ðèñ. 11.27

(ðèñ. 11.27). Ïðåäïîëîæèì, ÷òî íóæíî

ïåðåíåñòè ââåðõ ïî øêàëå ÷àñòîò íà çíà-

÷åíèå w ãàðìîíè÷åñêîå íèçêî÷àñòîòíîå

êîëåáàíèå ñ ÷àñòîòîé W:

(

)

cos.

uUt

Ïîäàäèì íà âõîä íåëèíåéíîãî ðåçî-

íàíñíîãî óñèëèòåëÿ, êðîìå ýòîãî êîëåáà-

íèÿ, òàêæå âûñîêî÷àñòîòíîå êîëåáàíèå ñ

÷àñòîòîé w:

(

)

cos.

uUt

Àìïëèòóäû íàïðÿæåíèé ñìåùåíèÿ

, íèçêî÷àñòîòíîãî U

è âûñîêî÷àñ-

òîòíîãî U

êîëåáàíèé âûáåðåì òàê,

÷òîáû ðàáîòàòü íà ó÷àñòêå ÂÀÕ, êîòî-

ðûé äîñòàòî÷íî òî÷íî àïïðîêñèìèðóåòñÿ

ïîëèíîìîì âòîðîé ñòåïåíè

( ) ( ) ( )

Ê012

ÁÝÁÝ0ÁÝ0

iFaaa

uuUuU

==++

(11.15)

Íàïðÿæåíèå íà ó÷àñòêå áàçà%ýìèòòåð

ÁÝ0

coscos.

uUUtUt

=+W+w

Ïîñëå ïîäñòàíîâêè ýòîãî âûðàæåíèÿ â çàâèñèìîñòü (11.15) â

ôîðìóëå äëÿ òîêà ïîÿâëÿþòñÿ ãàðìîíè÷åñêèå êîëåáàíèÿ ñ ÷àñòîòà-

ìè W, w, 2W, 2w è ñ ñóììàðíîé è ðàçíîñòíîé êîìáèíàöèîííûìè

÷àñòîòàìè w + W è w $ W.

Êîëåáàòåëüíûé êîíòóð ðåçîíàíñíîãî óñèëèòåëÿ íàñòðîåí íà ÷à-

ñòîòó w + W è âûäåëÿåò èç ñïåêòðàëüíîãî ñîñòàâà òîêà êîëåáàíèå

(

)

(

)

cos.

iaUUt

w+WWw

w+W

289

)

Ðèñ. 11.29

Âûäåëåííîå êîëåáàíèå òîêà ñîçäàåò íà ðåçîíàíñíîì ñîïðîòèâëåíèè

êîíòóðà R

0ý

ïàäåíèå íàïðÿæåíèÿ

(

)

(

)

(

)

âûõ20ý

coscos,

mmm

uaRUUtUt

Ww+W

w+Ww+W

êîòîðîå è ÿâëÿåòñÿ âûõîäíûì ñèãíàëîì ïðåîáðàçîâàòåëÿ ÷àñòîòû.

Â ðåàëüíûõ ñèñòåìàõ ñâÿçè ïåðåäàâàåìûé íèçêî÷àñòîòíûé ñèã-

íàë íå ÿâëÿåòñÿ ãàðìîíè÷åñêèì, à èìååò ñëîæíûé ñïåêòð U

(w)

(ðèñ. 11.28, à), ò. å. ñîñòîèò èç ñóììû ãàðìîíè÷åñêèõ êîëåáàíèé ñ

÷àñòîòàìè W

, W

, ... .

Åñëè ýòîò ñèãíàë âìåñòå ñ âûñîêî÷àñòîòíûì êîëåáàíèåì u

(t)

ïîäàòü íà íåëèíåéíûé ýëåìåíò, òî â ñïåêòðå òîêà I

(w)

(ðèñ. 11.28, á), ïðîòåêàþùåãî ÷åðåç ÍÝ, áóäóò ïðèñóòñòâîâàòü ïî-

ëåçíûå ïðîäóêòû ïðåîáðàçîâàíèÿ $ êîìáèíàöèîííûå ÷àñòîòû w +

+ W

, w + W

, ... . ×òîáû îòôèëüòðîâàòü òîêè ñ ýòèìè ÷àñ-

òîòàìè, íåäîñòàòî÷íî âîñïîëüçîâàòüñÿ îäèíî÷íûì êîëåáàòåëüíûì

êîíòóðîì, ïîñêîëüêó îí íå ñìîæåò îáåñïå÷èòü õîðîøóþ ôèëüòðà-

öèþ ïîëåçíûõ ïðîäóêòîâ ïðåîáðàçîâàíèÿ. Åãî ìîæíî çàìåíèòü â

ñõåìå ðèñ. 11.27 îáû÷íîé ðåçèñ-

òèâíîé íàãðóçêîé, à íà âûõîäå

ñõåìû âêëþ÷èòü ýëåêòðè÷åñêèé

ôèëüòð ñ õàðàêòåðèñòèêîé îñëàá-

ëåíèÿ (íà ðèñ. 11.28, á îíà

ïîêàçàíà øòðèõîâîé ëèíèåé),

îáåñïå÷èâàþùåé íåîáõîäèìóþ

ñòåïåíü ïîäàâëåíèÿ íåñóùåãî

êîëåáàíèÿ ñ ÷àñòîòîé w.

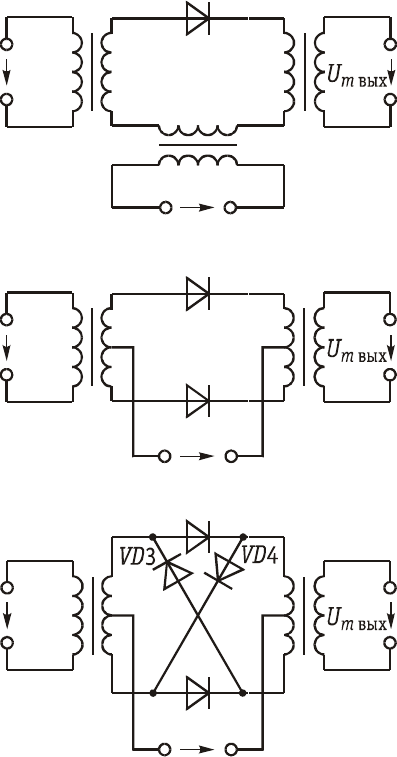
Ïðèâåäåì åùå íåñêîëüêî

ïðàêòè÷åñêèõ ñõåì ïðåîáðàçî-

âàòåëåé ÷àñòîòû. Íà ðèñ. 11.29

ïðåäñòàâëåíû äèîäíûå ïðåîáðà-

çîâàòåëè: îäíîòàêòíûé (à),

äâóõòàêòíûé èëè áàëàíñíûé

(á) è êîëüöåâîé (â), ðàáîòà-

þùèå â ðåæèìå áîëüøèõ àìï-

ëèòóä êîëåáàíèÿ ÷àñòîòû w,

ò. å. â ðåæèìå àïïðîêñèìàöèè

ÂÀÕ äèîäîâ ëèíåéíî-ëîìàíûìè

ôóíêöèÿìè.

Â áàëàíñíûõ è êîëüöåâûõ

ïðåîáðàçîâàòåëÿõ ãîðàçäî ìåíü-

øå ïîáî÷íûõ ïðîäóêòîâ ïðåîáðà-

çîâàíèÿ; òåì ñàìûì çíà÷èòåëüíî

îáëåã÷àþòñÿ òðåáîâàíèÿ ê ôèëü-

òðó, âûäåëÿþùåìó ïîëåçíûå êî-

ëåáàíèÿ.

290

Âîïðîñû è çàäàíèÿ äëÿ ñàìîïðîâåðêè

1. Êàêîâî ÷èñëî ãàðìîíè÷åñêèõ ñîñòàâëÿþùèõ ðåàêöèè ïðè ïîëè-

íîìèàëüíîé àïïðîêñèìàöèè ÂÀÕ íåëèíåéíîãî ýëåìåíòà è ãàð-

ìîíè÷åñêîì âîçäåéñòâèè?

2. Â ÷åì ïðèíöèïèàëüíîå îòëè÷èå ñïåêòðîâ ïðè ïîëèíîìèàëüíîé

àïïðîêñèìàöèè ÂÀÕ íåëèíåéíîãî ýëåìåíòà ïðè âîçäåéñòâèè ïî-

ðîçíü äâóõ ãàðìîíè÷åñêèõ êîëåáàíèé ñ ÷àñòîòàìè w

è w

è ïðè

ñîâìåñòíîì èõ âîçäåéñòâèè?

3. ×òî íàçûâàåòñÿ óãëîì îòñå÷êè è êàê îí çàâèñèò îò íàïðÿæåíèÿ

ñìåùåíèÿ è àìïëèòóäû ãàðìîíè÷åñêîãî âîçäåéñòâèÿ?

4. Ïðè êàêîì óãëå îòñå÷êè àìïëèòóäû ãàðìîíè÷åñêèõ ñîñòàâëÿþ-

ùèõ ðåàêöèè ïðÿìî ïðîïîðöèîíàëüíû àìïëèòóäå ãàðìîíè÷åñêî-

ãî âîçäåéñòâèÿ è ïî÷åìó?

5. Êàêèìè êîýôôèöèåíòàìè ïðè ïîëèíîìèàëüíîé àïïðîêñèìàöèè

ÂÀÕ îïðåäåëÿþòñÿ àìïëèòóäû ÷åòíûõ (íå÷åòíûõ) ãàðìîíèê ðåàê-

öèè ïðè ãàðìîíè÷åñêîì âîçäåéñòâèè? Ïîêàæèòå ýòî íà ïðèìåðå.

6. Ïðè êàêèõ óñëîâèÿõ â ðåçîíàíñíîì óñèëèòåëå, ðàáîòàþùåì â ðåæè-

ìå «áîëüøîãî» ñèãíàëà, ò. å. â íåëèíåéíîì ðåæèìå, àìïëèòóäà ðå-

àêöèè è ãàðìîíè÷åñêîãî âîçäåéñòâèÿ èìåþò ëèíåéíóþ çàâèñèìîñòü?

7. Íàïèøèòå âîçìîæíûå ÷àñòîòû ãàðìîíè÷åñêèõ ñîñòàâëÿþùèõ ðå-

àêöèè â ýëåêòðè÷åñêîé öåïè ïðè àïïðîêñèìàöèè ÂÀÕ íåëèíåé-

íîãî ýëåìåíòà ïîëèíîìîì ÷åòâåðòîãî ïîðÿäêà ïðè áèãàðìîíè÷å-

ñêîì âîçäåéñòâèè.

8. Êàê èçìåíÿåòñÿ ÊÏÄ è âûõîäíàÿ ìîùíîñòü ðåçîíàíñíîãî óñèëè-

òåëÿ îò óãëà îòñå÷êè?

9. Íà êàêóþ ÷àñòîòó íàñòðàèâàþò ïàðàëëåëüíûé êîëåáàòåëüíûé

êîíòóð è êàêèì âûáèðàþò óãîë îòñå÷êè â óìíîæèòåëÿõ ÷àñòîòû?

×åì îãðàíè÷åíà êðàòíîñòü óìíîæåíèÿ ÷àñòîòû íà ïðàêòèêå?

10. Êàê èçìåíÿåòñÿ âûïðÿìëåííîå ïîñòîÿííîå íàïðÿæåíèå U

îò îòíîøåíèÿ ñîïðîòèâëåíèÿ äèîäà ê ñîïðîòèâëåíèþ íàãðóçêè

11. Â ÷åì ïðåèìóùåñòâî äâóõïîëóïåðèîäíîãî âûïðÿìèòåëÿ ïî

ñðàâíåíèþ ñ îäíîïîëóïåðèîäíûì è ïî÷åìó?

12. ÂÀÕ íåëèíåéíîãî ðåçèñòèâíîãî ýëåìåíòà àïïðîêñèìèðîâàíà

ïîëèíîìîì

013

iaauau

=++

. Íàéäèòå ÷àñòîòû âñåõ ñîñòàâ-

ëÿþùèõ òîêà, åñëè ê ýëåìåíòó ïðèëîæåíî íàïðÿæåíèå:

à)

cos

uUt

, á)

cos

uUUt

=+w

Îòâåò: à) 0, w

, 3w

; á) 0, w

, 2w

, 3w

13. ÂÀÕ íåëèíåéíîãî ðåçèñòèâíîãî ýëåìåíòà àïïðîêñèìèðîâàíà

ïîëèíîìîì

5041,5

iuu

=++

mA. Ê ýëåìåíòó ïðèëîæåíî íà-

ïðÿæåíèå

4cos10

uUt

Â. Íàéäèòå çàâèñèìîñòü àìïëèòó-