Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.


241
Ïðèìåð. Ïðèìåíèì ìåòîä ýêâèâàëåíòíîãî ãåíåðàòîðà ê ñõåìå ðèñ. 10.13, à,
ãäå U
01
= 14 Â, J
02
= 10 ìÀ, R
1
= 1 êÎì, I
í
= 10
$5
U
í
2
. Èç ðèñóíêà ñëåäóåò,
÷òî íàïðÿæåíèå U
ýã
ïðè îòêëþ÷åíèè ÍÝ ðàâíî
ýã 02101
24B,
UJRU
=+=
à ýêâèâàëåíòíîå ñîïðîòèâëåíèå R
ý
= R
1
= 1 êÎì.  ñîîòâåòñòâèè ñ ÇÍÊ
(ðèñ. 10.13, á) èìååì
(
)
33
íýãí1í
102410.
IUURU
--
=-=-+×
Ïîñòðîåíèå ãðàôèêîâ ïðÿìîé ëèíèè è ÂÀÕ íåëèíåéíîãî ýëåìåíòà ïîêàçà-
íî íà ðèñ. 10.13, â. Ïåðåñå÷åíèå ýòèõ êðèâûõ äàåò êîîðäèíàòû ðàáî÷åé òî÷êè:
I
í
= 4 ìÀ è U
í
= 20 Â.
10.3. Ãðàôè÷åñêèå ìåòîäû ðàñ÷åòà öåïåé ñ íåëèíåéíûìè
ðåçèñòèâíûìè ÷åòûðåõïîëþñíèêàìè
Ðàññìîòðèì çàäà÷ó àíàëèçà ðåæèìà ïîñòîÿííîãî òîêà â ðåçè-
ñòèâíîé ýëåêòðè÷åñêîé öåïè ñ íåëèíåéíûì ÷åòûðåõïîëþñíèêîì
(ðèñ. 10.14).
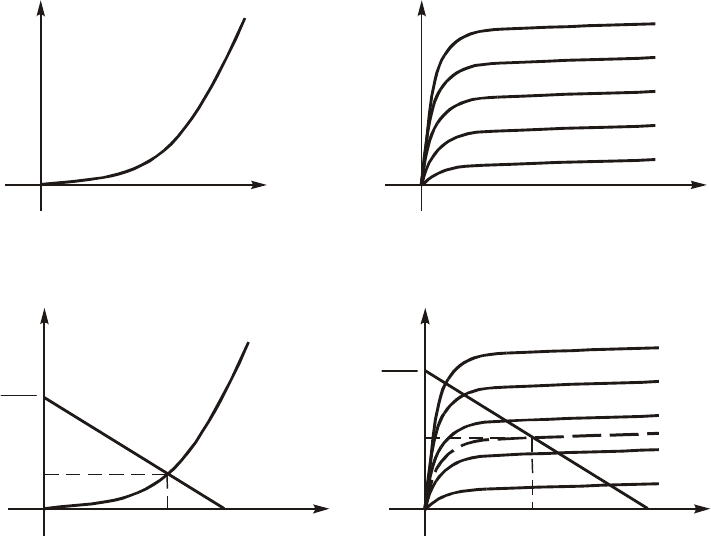
Ïóñòü âõîäíàÿ ÂÀÕ è ñåìåéñòâî âûõîäíûõ ÂÀÕ áóäóò èìåòü
âèä ïîêàçàííûé íà ðèñ. 10.15, à è á; óïðàâëÿþùèì ïàðàìåòðîì
äëÿ ñåìåéñòâà âûõîäíûõ õàðàêòåðèñòèê ÷åòûðåõïîëþñíèêà ÿâëÿåò-
ñÿ åãî âõîäíîé òîê I
1
.
Çàäà÷à íàõîæäåíèÿ âõîäíûõ íàïðÿæåíèÿ U
1
= U
10
è òîêà I
1
=
= I
10
ñâîäèòñÿ ê çàäà÷å íàõîæäåíèÿ ðàáî÷åé òî÷êè íà âõîäíîé
âîëüò-àìïåðíîé õàðàêòåðèñòèêå i
1
= F
1
(u
1
). Îíà ðåøàåòñÿ ñ ïîìî-
ùüþ ãðàôè÷åñêèõ ïîñòðîåíèé, êîòîðûå ïîëíîñòüþ àíàëîãè÷íû ðàñ-
ñìîòðåííûì â § 10.2 (ðèñ. 10.16, à).
ÍÝ
I
1
R
1
+
-
J
02
+
-
U
í
+
-
U
01
+
-
U
1
I
í
U
ýã
+
+
ÍÝ
0
i,
ìÀ
u
í
, Â
10
U
í
=
2030
10
20
30
U
í
I
í
R
ý
à
)
á
)
â
)
I
í
=
4
1
2
Ðèñ. 10.13
U
ã1
+
R
1
I
1
Íåëèíåéíûé
ðåçèñòèâíûé
4-ïîëþñíèê
U
ã2
+
R
2
I
2
U
1
U
2
+ +
Ðèñ. 10.14
242
Íàéäåííîìó âõîäíîìó òîêó I
1
= I
10
ñîîòâåòñòâóåò îïðåäåëåííàÿ
âûõîäíàÿ âîëüò-àìïåðíàÿ õàðàêòåðèñòèêà i
2
= F
2
(u
2
). Îíà ìîæåò
áûòü èçìåðåíà èëè, êàê ýòî îáû÷íî äåëàåòñÿ, îïðåäåëåíà ïî ñåìåé-
ñòâó âûõîäíûõ âîëüò-àìïåðíûõ õàðàêòåðèñòèê ÷åòûðåõïîëþñíèêà
èç ñïðàâî÷íèêà. Äëÿ ýòîãî íåîáõîäèìî ïðîâåñòè ëèíåéíîå èíòåð-
ïîëèðîâàíèå äâóõ õàðàêòåðèñòèê ñåìåéñòâà ñ áëèæàéøèìè çíà÷å-
íèÿìè ïàðàìåòðîâ I
1
< I
10
è I
1
> I
10
. Íà ðèñ. 10.16, á ýòà õàðàêòå-
ðèñòèêà èçîáðàæåíà øòðèõîâîé ëèíèåé.
Âûõîäíîé òîê I
2
è âûõîäíîå íàïðÿæåíèå U
2
(ñì. ðèñ. 10.14)
ñâÿçàíû ìåæäó ñîáîé ëèíåéíîé çàâèñèìîñòüþ I
2
= (U
ã2
%U
2
)/R
2
,
êîòîðàÿ íà ðèñ. 10.16, á ïðåäñòàâëÿåò ñîáîé ïðÿìóþ, ïðîõîäÿùóþ
÷åðåç òî÷êè U
2
= U
ã2
íà îñè àáñöèññ è I
2
= U
ã2
/R
2
íà îñè îðäèíàò.
Òî÷êà ïåðåñå÷åíèÿ çàâèñèìîñòåé I
2
= (U
ã2
%U
2
)/R
2
è i
2
=
F
2
(u
2
) ïðè I
1
= I
10
è îïðåäåëÿåò ðàáî÷óþ òî÷êó (U
20
, I
20
) íà âû-
õîäíûõ õàðàêòåðèñòèêàõ ÷åòûðåõïîëþñíèêà.
Äàëüíåéøèé àíàëèç ðàññìàòðèâàåìîé öåïè ìîæåò áûòü ñâÿçàí ñ
íàõîæäåíèåì íàïðÿæåíèé è òîêîâ â âåòâÿõ âõîäíîé è âûõîäíîé
öåïåé, åñëè äî àíàëèçà ýòè öåïè áûëè çàìåíåíû ýêâèâàëåíòíûìè
ãåíåðàòîðàìè.
10.4. Ýêâèâàëåíòíûå ïðåîáðàçîâàíèÿ ñõåì
ñ íåëèíåéíûìè ýëåìåíòàìè
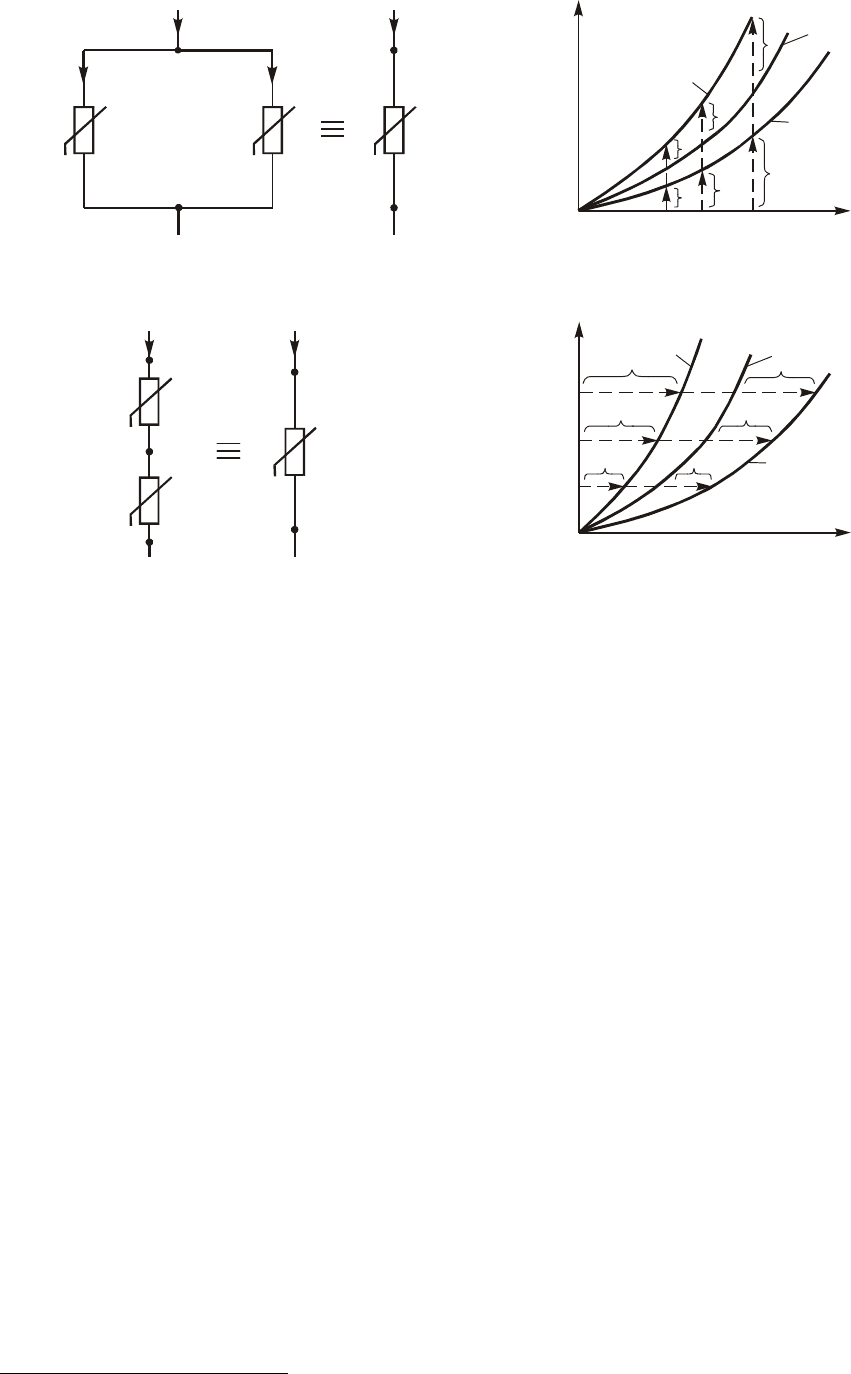
Ñóòü ýêâèâàëåíòíûõ ïðåîáðàçîâàíèé ñîñòîèò â çàìåíå ó÷àñòêîâ
öåïè ñ ïàðàëëåëüíûì èëè ïîñëåäîâàòåëüíûì ñîåäèíåíèåì âåòâåé
á
)
u
2
i
2
à
)
0
u
1
i
1
0
i
1
IV
i
1
V
i
1
III
i
1
II
i
1
I
Ðèñ. 10.15
á
)
u
2
U
ã2
U
20
i
2
à
)
0
I
20
R
2
U
ã2
I
10
u
1
U
ã1
U
10
i
1
0
I
10
R
1
U
ã1
Ðèñ. 10.16
243
+
-
u
+
-
i
i
2
i
1
i
u
i
u
Fu
1
()
Fu
2
()
Fu
ý
()
Ðèñ. 10.17 Ðèñ. 10.18
+
-
i
+
-
i
+
u
2
u
1
-
u
i
u
Fu
1
()
Fu
2
()
Fu
ý
()
Ðèñ. 10.19 Ðèñ. 10.20
îäíîé ýêâèâàëåíòíîé âåòâüþ ïóòåì ñóììèðîâàíèÿ èõ òîêîâ èëè íà-
ïðÿæåíèé. Ðå÷ü çäåñü èäåò î ñóììèðîâàíèè îðäèíàò èëè àáñöèññ
çàäàííûõ õàðàêòåðèñòèê âåòâåé öåïè. Ýòîò ìåòîä îñîáåííî ýôôåê-
òèâåí â ñëó÷àå öåïè ñ îäíèì èñòî÷íèêîì: öåïü ïðåäñòàâëÿåòñÿ èñ-
òî÷íèêîì è îäíèì ýêâèâàëåíòíûì íåëèíåéíûì ýëåìåíòîì.
Ïóñòü äâà ÍÝ ñ óðàâíåíèÿìè (ÂÀÕ) i
1
= F
1
(u
1
) è i
2
= F
2
(u
2
)
âêëþ÷åíû ïàðàëëåëüíî (ðèñ. 10.17)
*
.
Íåîáõîäèìî íàéòè óðàâíåíèå ÍÝ, ýêâèâàëåíòíîãî äàííîìó ñî-
åäèíåíèþ ýëåìåíòîâ. Òàê êàê ýëåìåíòû ñîåäèíåíû ïàðàëëåëüíî, òî
u
1
= u
2
= u, à ïî ïåðâîìó çàêîíó Êèðõãîôà i = i
1
+ i
2
. Âûïîëíèì
ñëîæåíèå òîêîâ ãðàôè÷åñêè, êàê ïîêàçàíî íà ðèñ. 10.18. Çàäàåìñÿ
çíà÷åíèåì íàïðÿæåíèÿ. Ïðè ýòîì çíà÷åíèè íàïðÿæåíèÿ íàõîäèì
òîêè ÍÝ è ñóììèðóåì èõ. Çàäàåìñÿ íîâûì çíà÷åíèåì íàïðÿæåíèÿ
è îïÿòü ñóììèðóåì òîêè. Òàêèì îáðàçîì, íàõîäèì ñåðèþ òî÷åê, ñî-
åäèíÿÿ êîòîðûå, ïîëó÷àåì ÂÀÕ ýêâèâàëåíòíîãî ÍÝ.
Ðàññìîòðèì ïîñëåäîâàòåëüíîå ñîåäèíåíèå ÍÝ (ðèñ. 10.19). Â
äàííîì ñëó÷àå i
1
= i
2
= i, a u = u
1
+ u
2
. Ïðîöåññ îïðåäåëåíèÿ ÂÀÕ
ÍÝ ïîêàçàí íà ðèñ.10.20. Çàìåòèì, ÷òî ðàññìîòðåííûå ïðåîáðàçî-
âàíèÿ ïðèìåíèìû è â ñëó÷àå, êîãäà ïîñëåäîâàòåëüíî èëè ïàðàë-
ëåëüíî ñîåäèíåíû íåñêîëüêî íåëèíåéíûõ, à òàêæå ëèíåéíûõ ýëå-
ìåíòîâ.
*
Ïîñêîëüêó ïðèâîäèìûå íèæå ðàññóæäåíèÿ ñïðàâåäëèâû íå òîëüêî äëÿ ðåæèìà ïî-
ñòîÿííîãî, íî è äëÿ ðåæèìà ïåðåìåííîãî òîêà, â äàëüíåéøåì áóäåì èñïîëüçîâàòü
äëÿ îáîçíà÷åíèé íàïðÿæåíèé è òîêîâ ìàëûå (ñòðî÷íûå) áóêâû.
244
U
2
i
u
F
ý
1
2
3
2-3
13
I
+
-
à
)
á
)
Ðèñ. 10.21
U
+
-
+
-
u
2
ÍÝ
2
i
R
i
2
ÍÝ
1
+ -
i
R
0
10
20
30
40
50
60
70
80
2
4
6
u
, Â
i
, ìÀ
Fu
1
()
Fu
2
()
ÍÝ
2
ÍÝ
1
Ðèñ. 10.22 Ðèñ. 10.23
0
10
20
30
40
50
60
70
80
2 4 6
u
, Â
i
, ìÀ
Fu
ý2
()
i
R
à
)
0
10
20
30
40
50
60
70
80
2 4 6
u
, Â
i
, ìÀ
Fu
ý1
()
Fu
ý2
()
Fu
1
()
á
)
Fu
2
()
Ðèñ. 10.24
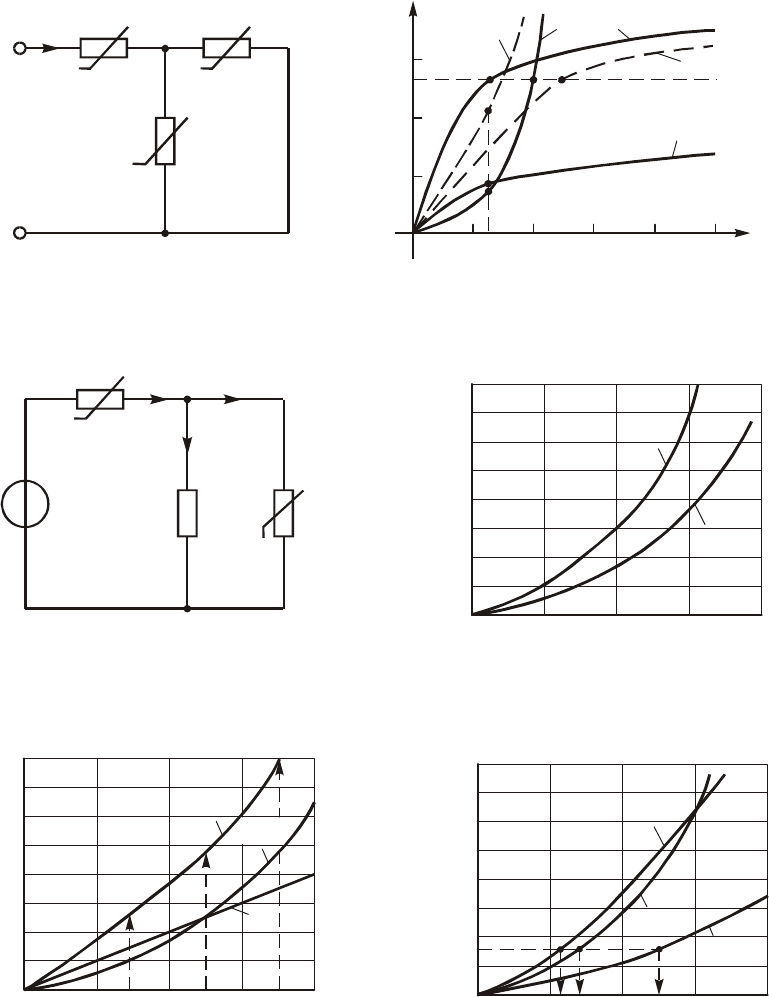
Ïðèìåð. Íà ðèñ. 10.21, à ïîêàçàíà ïîäêëþ÷åííàÿ ê èñòî÷íèêó íàïðÿæåíèÿ
öåïü èç òðåõ ðåçèñòèâíûõ ÍÝ (ðèñ. 10.21, á). Ñóììèðîâàíèå îðäèíàò õàðàê-
òåðèñòèê ýëåìåíòîâ 2 è 3, ñîåäèíåííûõ ïàðàëëåëüíî, äàåò ýêâèâàëåíòíóþ õà-
ðàêòåðèñòèêó 2%3. Ñóììèðóÿ àáñöèññû ïîñëåäíåé ñ àáñöèññàìè êðèâîé 1, ïî-
ëó÷àåì ýêâèâàëåíòíóþ õàðàêòåðèñòèêó íåëèíåéíîé öåïè F
ý
. Èç ãðàôèêîâ ðèñ.
10.21, á ìîæíî, çàäàâàÿñü íàïðÿæåíèåì íà âõîäå, ïîëó÷èòü òîêè è íàïðÿæå-
íèÿ âåòâåé.
Ïðèìåð. Ðàññ÷èòàåì íàïðÿæåíèÿ è òîêè â öåïè, ñõåìà êîòîðîé èçîáðàæåíà
íà ðèñ. 10.22, ãäå U = 5 Â, R = 500 Îì, à ÂÀÕ ÍÝ çàäàíû ãðàôèêàìè íà
ðèñ. 10.23.
245
Ïîñêîëüêó ÂÀÕ çàäàíû ãðàôèêàìè, òî ïðè ðåøåíèè âîñïîëüçóåìñÿ ãðàôè-
÷åñêèìè ïîñòðîåíèÿìè. Íàéäåì ÂÀÕ i = F
ý2
(u) äâóõïîëþñíèêà, ýêâèâàëåíò-
íîãî ïàðàëëåëüíîìó ñîåäèíåíèþ ëèíåéíîãî ñîïðîòèâëåíèÿ R è ÍÝ
2
. Äëÿ ýòîãî
ïåðåíåñåí ÂÀÕ ÍÝ
2
íà íîâûé ðèñóíîê è ïîñòðîèì ÂÀÕ ëèíåéíîãî ýëåìåíòà
(ðèñ. 10.24, à). Íà ýòîì æå ðèñóíêå ïîêàçàíà ýêâèâàëåíòíàÿ ÂÀÕ i = F
ý2
(u).
Ïåðåíåñåì ýòó ýêâèâàëåíòíóþ ÂÀÕ è ÂÀÕ ÍÝ
1
íà ðèñ. 10.24, á è íàéäåì
ÂÀÕ ýêâèâàëåíòíîãî äâóõïîëþñíèêà i = F
ý1
(u), êîòîðûé ïðèñîåäèíÿåòñÿ ê
çàæèìàì èñòî÷íèêà.
Ïî ðèñ. 10.24, á ïî êðèâîé i = F
ý1
(u) íàõîäèì, ÷òî íàïðÿæåíèþ u = 5 Â
ñîîòâåòñòâóåò òîê i = 16 ìÀ, ïî êðèâîé i = F
1
(u) $ íàïðÿæåíèå íà ÍÝ
1
u
1
=
= 2,8 B è no-êðèâîé i = F
ý2
(u) $ íàïðÿæåíèå íà ïàðàëëåëüíîì ñîåäèíåíèè R
è ÍÝ
2
u
2
= 2,2 Â. Çíàÿ ýòî íàïðÿæåíèå, ïî ãðàôèêàì ðèñ. 10.24, à íàõîäèì
i
R
= 11 ìÀ è i
2
= 5 ìÀ.
10.5. Àíàëèòè÷åñêîå ïðåäñòàâëåíèå âîëüò-àìïåðíûõ
õàðàêòåðèñòèê
×àñòî íåîáõîäèìî èìåòü àíàëèòè÷åñêèå âûðàæåíèÿ äëÿ âîëüò-
àìïåðíûõ õàðàêòåðèñòèê íåëèíåéíûõ ýëåìåíòîâ. Ýòè âûðàæåíèÿ
ìîãóò ëèøü ïðèáëèæåííî ïðåäñòàâëÿòü ÂÀÕ, ïîñêîëüêó ôèçè÷å-
ñêèå çàêîíîìåðíîñòè, êîòîðûì ïîä÷èíÿþòñÿ çàâèñèìîñòè ìåæäó
íàïðÿæåíèÿìè è òîêàìè â ýëåêòðîííûõ è ïîëóïðîâîäíèêîâûõ ïðè-
áîðàõ, íå âûðàæàþòñÿ àíàëèòè÷åñêè.
Çàäà÷à ïðèáëèæåííîãî àíàëèòè÷åñêîãî ïðåäñòàâëåíèÿ ôóíêöèè,
çàäàííîé ãðàôè÷åñêè èëè òàáëèöåé çíà÷åíèé, â çàäàííûõ ïðåäåëàõ
èçìåíåíèÿ åå àðãóìåíòà (íåçàâèñèìîé ïåðåìåííîé) ïðåäïîëàãàåò,
âî-ïåðâûõ, âûáîð àïïðîêñèìèðóþùåé ôóíêöèè, ò. å. ôóíêöèè, ñ
ïîìîùüþ êîòîðîé ïðèáëèæåííî ïðåäñòàâëÿåòñÿ çàäàííàÿ çàâèñè-
ìîñòü, è, âî-âòîðûõ, âûáîð êðèòåðèÿ îöåíêè «áëèçîñòè» ýòîé çàâè-
ñèìîñòè è àïïðîêñèìèðóþùåé åå ôóíêöèÿ.
 êà÷åñòâå àïïðîêñèìèðóþùèõ ôóíêöèé èñïîëüçóþòñÿ, ÷àùå
âñåãî, àëãåáðàè÷åñêèå ïîëèíîìû, íåêîòîðûå äðîáíûå ðàöèîíàëü-
íûå è òðàíñöåíäåíòíûå ôóíêöèè èëè ñîâîêóïíîñòü îòðåçêîâ ïðÿ-
ìûõ ëèíèé.
Áóäåì ñ÷èòàòü, ÷òî ÂÀÕ íåëèíåéíîãî ýëåìåíòà i = F(u) çàäàíà
ãðàôè÷åñêè, ò. å. îïðåäåëåíà â êàæäîé òî÷êå èíòåðâàëà U
min
„
u
„
„
U
max
, è ïðåäñòàâëÿåò ñîáîé îäíîçíà÷íóþ íåïðåðûâíóþ ôóíêöèþ
ïåðåìåííîé u. Òîãäà çàäà÷à àíàëèòè÷åñêîãî ïðåäñòàâëåíèÿ âîëüò-
àìïåðíîé õàðàêòåðèñòèêè ìîæåò ðàññìàòðèâàòüñÿ êàê çàäà÷à àï-
ïðîêñèìàöèè çàäàííîé ôóíêöèè x(x) âûáðàííîé àïïðîêñèìèðóþ-
ùåé ôóíêöèåé f(x).
Î áëèçîñòè àïïðîêñèìèðóþùåé f(x) è àïïðîêñèìèðóåìîé x(x)
ôóíêöèé èëè, èíûìè ñëîâàìè, î ïîãðåøíîñòè àïïðîêñèìàöèè,
îáû÷íî ñóäÿò ïî íàèáîëüøåìó àáñîëþòíîìó çíà÷åíèþ ðàçíîñòè
ìåæäó ýòèìè ôóíêöèÿìè â èíòåðâàëå àïïðîêñèìàöèè à
„
õ
„
b,
ò. å. ïî âåëè÷èíå

246
(
)
(
)
max.
fxx
L=-x
(10.3)
×àñòî êðèòåðèåì áëèçîñòè âûáèðàåòñÿ ñðåäíåå êâàäðàòè÷åñêîå
çíà÷åíèå ðàçíîñòè ìåæäó óêàçàííûìè ôóíêöèÿìè â èíòåðâàëå àï-
ïðîêñèìàöèè, ò. å. âåëè÷èíà
( ) ( )
[ ]
2
1
b
a
fxxdx
ba
L=-x
-
ò
. (10.4)
Èíîãäà ïîä áëèçîñòüþ äâóõ ôóíêöèé f(x) è x(x) ïîíèìàþò ñîâ-
ïàäåíèå â çàäàííîé òî÷êå x = X
0
ñàìèõ ôóíêöèé è n + 1 èõ ïðîèç-
âîäíûõ.
Íàèáîëåå ðàñïðîñòðàíåííûì ñïîñîáîì ïðèáëèæåíèÿ àíàëèòè÷å-
ñêîé ôóíêöèè ê çàäàííîé ÿâëÿåòñÿ èíòåðïîëÿöèÿ (ìåòîä âûáðàí-
íûõ òî÷åê), êîãäà äîáèâàþòñÿ ñîâïàäåíèÿ ôóíêöèé f(x) è x(x) â
âûáðàííûõ òî÷êàõ (óçëàõ èíòåðïîëÿöèè) õ
k
, k = 0, 1, 2, ..., n.
Ïîãðåøíîñòü àïïðîêñèìàöèè ìîæåò áûòü äîñòèãíóòà òåì ìåíü-
øåé, ÷åì áîëüøå ÷èñëî âàðüèðóåìûõ ïàðàìåòðîâ âõîäèò â àïïðîê-
ñèìèðóþùóþ ôóíêöèþ, ò. å., íàïðèìåð, ÷åì âûøå ñòåïåíü àïïðîê-
ñèìèðóþùåãî ïîëèíîìà èëè ÷åì áîëüøå ÷èñëî îòðåçêîâ ïðÿìûõ
ñîäåðæèò àïïðîêñèìèðóþùàÿ ëèíåéíî-ëîìàíàÿ ôóíêöèÿ. Îäíî-
âðåìåííî ñ ýòèì, åñòåñòâåííî, ðàñòåò îáúåì âû÷èñëåíèé êàê ïðè
ðåøåíèè çàäà÷è àïïðîêñèìàöèè, òàê è ïðè ïîñëåäóþùåì àíàëèçå
íåëèíåéíîé öåïè. Ïðîñòîòà ýòîãî àíàëèçà íàðÿäó ñ îñîáåííîñòÿìè
àïïðîêñèìèðóåìîé ôóíêöèè â ïðåäåëàõ èíòåðâàëà àïïðîêñèìàöèè
ñëóæèò îäíèì èç âàæíåéøèõ êðèòåðèåâ ïðè âûáîðå òèïà àïïðîê-
ñèìèðóþùåé ôóíêöèè.
 çàäà÷àõ àïïðîêñèìàöèè âîëüò-àìïåðíûõ õàðàêòåðèñòèê ýëåê-
òðîííûõ è ïîëóïðîâîäíèêîâûõ ïðèáîðîâ ñòðåìèòüñÿ ê âûñîêîé
òî÷íîñòè èõ âîñïðîèçâåäåíèÿ, êàê ïðàâèëî, íåò íåîáõîäèìîñòè
ââèäó çíà÷èòåëüíîãî ðàçáðîñà õàðàêòåðèñòèê ïðèáîðîâ îò îáðàçöà
ê îáðàçöó è ñóùåñòâåííîãî âëèÿíèÿ íà íèõ äåñòàáèëèçèðóþùèõ
ôàêòîðîâ, íàïðèìåð, òåìïåðàòóðû â ïîëóïðîâîäíèêîâûõ ïðèáîðàõ.
 áîëüøèíñòâå ñëó÷àåâ äîñòàòî÷íî «ïðàâèëüíî» âîñïðîèçâåñòè îá-
ùèé óñðåäíåííûé õàðàêòåð çàâèñèìîñòè i = F(u) â ïðåäåëàõ åå ðà-
áî÷åãî èíòåðâàëà.
Ïîëèíîìèàëüíàÿ àïïðîêñèìàöèÿ.  êà÷åñòâå àïïðîêñèìèðóþ-
ùåé ôóíêöèè â çàäà÷àõ àíàëèòè÷åñêîãî ïðåäñòàâëåíèÿ âîëüò-
àìïåðíûõ õàðàêòåðèñòèê î÷åíü ÷àñòî èñïîëüçóþòñÿ àëãåáðàè÷åñêèå
ïîëèíîìû
(
)
2
012
n
n
fxaaxaxax
=++++
K
(10.5)
òîé èëè èíîé ñòåïåíè.
Ïîñòîÿííûå
012
,,,,
n
aaaa
K
ïðåäñòàâëÿþò ñîáîé âàðüèðóåìûå
ïàðàìåòðû, çíà÷åíèÿ êîòîðûõ âûáèðàþòñÿ òàêèìè, ÷òîáû â èíòåð-
âàëå àïïðîêñèìàöèè a
„
x
„
b ñâåñòè ê ìèíèìóìó ïîãðåøíîñòü
àïïðîêñèìàöèè â ñîîòâåòñòâèè ñ âûáðàííûì êðèòåðèåì áëèçîñòè.
247
 ïðîñòåéøåì ñëó÷àå êðèòåðèåì áëèçîñòè ìîæåò ñëóæèòü ñîâïà-
äåíèå çíà÷åíèé àïïðîêñèìèðóþùåé è àïïðîêñèìèðóåìîé ôóíêöèé
â âîçìîæíî áîëüøåì ÷èñëå âûáðàííûõ òî÷åê, ðàñïîëîæåííûõ â
èíòåðâàëå àïïðîêñèìàöèè. Ñîîòâåòñòâóþùèé ìåòîä ïðèáëèæåííîãî
âîñïðîèçâåäåíèÿ ôóíêöèé íîñèò, êàê ìû óæå óïîìèíàëè, íàçâàíèå
èíòåðïîëèðîâàíèÿ, à äèñêðåòíûå òî÷êè, â êîòîðûõ òðåáóåòñÿ òî÷-
íîå ñîâïàäåíèå ôóíêöèé f(x) è x(x), íàçûâàþòñÿ óçëàìè èíòåðïî-
ëèðîâàíèÿ. Èõ ÷èñëî íà åäèíèöó ïðåâûøàåò ñòåïåíü èíòåðïîëè-
ðóþùåãî ïîëèíîìà. Äåéñòâèòåëüíî, çàïèñûâàÿ ðàâåíñòâî ôóíêöèé
f(x
k
) = x(x
k
) â êàæäîì èç óçëîâ èíòåðïîëèðîâàíèÿ x
k
, k = 0, 1,
2, ..., n, ïîëó÷èì ñèñòåìó èç n + 1 ëèíåéíûõ óðàâíåíèé
(
)
( )
( )
2
01020
00
2
01121
11
2
012
....................
n
n
n
n
n
nnnnn
aaxaxaxx
aaxaxaxx
aaxaxaxx
++++=x
ü
ï
ï
++++=x
ý
ï
++++=x
ï
þ
K
K
K
(10.6)
ñ òàêèì æå ÷èñëîì íåèçâåñòíûõ êîýôôèöèåíòîâ
012
,,,,
n
aaaa
K
èíòåðïîëèðóþùåãî ïîëèíîìà.
 òåîðèè èíòåðïîëèðîâàíèÿ ôóíêöèé äîêàçûâàåòñÿ, ÷òî ñèñòåìà
óðàâíåíèé (10.6) èìååò åäèíñòâåííîå ðåøåíèå. Åäèíñòâåííûì, ñëå-
äîâàòåëüíî, áóäåò è ðåøåíèå ðàññìàòðèâàåìîé çàäà÷è èíòåðïîëè-
ðîâàíèÿ âîëüò-àìïåðíîé õàðàêòåðèñòèêè ïîëèíîìîì âûáðàííîé
ñòåïåíè.
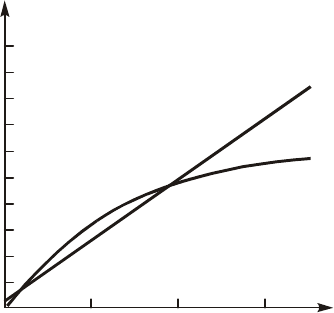
Ïðèâåäåì ïðîñòåéøèé ïðèìåð èíòåðïîëèðîâàíèÿ â èíòåðâàëå
0
„
x
„
1,5 ïîëèíîìîì ïåðâîé ñòåïåíè
(
)
01
fxaax
=+
ôóíêöèè
(
)
1
x
xe
-
x=-
, çàäàííîé àíàëèòè÷åñêè. Ðàñïîëîæèì óçëû èíòåðïî-
ëèðîâàíèÿ, à èõ äîëæíî áûòü n + 1 = 2, ïðè x
0
= 0,1 è x
1
= 1,0.
Òîãäà ñèñòåìà óðàâíåíèé îòíîñèòåëüíî èñêîìûõ êîýôôèöèåíòîâ a
0
è a
1
áóäåò òàêîé:
0,1
01
0,11
aae
-
+×=-
è
1
01
1
aae
-
+=-
. Èç åå ðå-
øåíèÿ ñëåäóåò à
0
= 0,036, a
1
= 0,597 è f(x) = 0,036 + 0,597x. Ãðà-
ôèêè ôóíêöèé f(x) è x(õ) ïðèâåäåíû íà ðèñ. 10.25. Îíè ïîêàçû-
âàþò, ÷òî òî÷íîñòü âîñïðîèçâåäåíèÿ çàäàííîé ôóíêöèè íåâåëèêà. Â
çàäàííîì èíòåðâàëå 0
„
x
„
1,5 íà-
èáîëüøàÿ ïîãðåøíîñòü |f(x)%x(õ)|,
ò. å. max|f(x)%x(õ)| íàõîäèòñÿ íà
îäíîé èç ãðàíèö èíòåðâàëà ïðè õ =
= 1,5 è ñîñòàâëÿåò 0,158. Åå ìîæíî
óìåíüøèòü, âûáðàâ äðóãèå óçëû
èíòåðïîëèðîâàíèÿ è, òåì áîëåå,
ïîâûñèâ ñòåïåíü èíòåðïîëèðóþùå-
ãî ïîëèíîìà. Òàê, ãðàôèêè òîé æå
ôóíêöèè
(
)
1
x
xe
-
x=-
è èíòåðïî-
ëèðóþùåãî ïîëèíîìà âòîðîé ñòå-
ïåíè ñ óçëàìè èíòåðïîëèðîâàíèÿ
x
0
= 0,15, x
1
= 0,6 è x
2
= 1,2 ïðàê-
0
fx
()
x
1
1,5
0,1
0,2
0,3
0,5
0,4
0,5
0,6
0,7
0,8
0,9
1
x
()
x
fx
()
x
()
x
Ðèñ. 10.25
248
òè÷åñêè ñîâïàäàþò. Íà ðèñ. 10.26 ïðèâåäåí ãðàôèê ðàçíîñòè ýòèõ
ôóíêöèé, èç êîòîðîãî ñëåäóåò, ÷òî ïîãðåøíîñòü â òîì æå çàäàííîì
èíòåðâàëå íå ïðåâûøàåò 0,026, ò. å. óìåíüøèëàñü ïî ñðàâíåíèþ ñ
ëèíåéíîé èíòåðïîëÿöèåé â 6 ðàç.
Îäíèì èç ýôôåêòèâíûõ ìåòîäîâ àïïðîêñèìàöèè ôóíêöèé, â êî-
òîðîì ïîãðåøíîñòü àïïðîêñèìàöèè êîíòðîëèðóåòñÿ âî âñåì èíòåð-
âàëå ïðèáëèæåíèÿ à x b, à íå â åãî äèñêðåòíûõ òî÷êàõ, ÿâëÿ-
åòñÿ ìåòîä íàèëó÷øåãî ðàâíîìåðíîãî ïðèáëèæåíèÿ (àïïðîêñèìà-
öèè) ôóíêöèé (ïðèáëèæåíèÿ ïî Ï.Ë. ×åáûøåâó).  ýòîì ìåòîäå
ïàðàìåòðû àïïðîêñèìèðóþùåé ôóíêöèè âûáèðàþòñÿ òàêèìè, ÷òî-
áû â èíòåðâàëå ïðèáëèæåíèÿ íàèáîëüøåå ïî àáñîëþòíîé âåëè÷èíå
îòêëîíåíèå ôóíêöèè f(x) îò íåïðåðûâíîé ôóíêöèè x(õ) áûëî áû
ìèíèìàëüíî âîçìîæíûì, èëè, èñïîëüçóÿ îáîçíà÷åíèÿ (10.3), ÷òîáû
â èíòåðâàëå à õ b
(
)
(
)
maxmin
fxxL=-x=. (10.7)
 ðàññìîòðåííîì âûøå ïðèìåðå ýòîìó êðèòåðèþ óäîâëåòâîðÿåò
ïîëèíîì f(õ) = 0,071 + 0,518õ. Íàèáîëüøèå åãî îòêëîíåíèÿ îò
ôóíêöèè
(
)
1
x
xe
-
x=-
â èíòåðâàëå 0 x 1,5 ðàñïîëîæåíû ïðè
x = 0, õ =x
m
= 0,658 è õ = 1,5 (ñì. ðèñ. 10.27), ïðè÷åì, ÷òî î÷åíü
âàæíî, âñå îíè ðàâíû ïî àáñîëþòíîé âåëè÷èíå. Ëåãêî ïîíÿòü, ÷òî
ëþáîå èçìåíåíèå íàêëîíà (à
1
) èëè óðîâíÿ (à
0
) ïîëèíîìà f(x), êî-
òîðîå âåäåò ê óìåíüøåíèþ ýêñòðåìàëüíîãî îòêëîíåíèÿ â äâóõ èç
òðåõ óêàçàííûõ òî÷åê, óâåëè÷èâàåò îòêëîíåíèÿ â îñòàâøåéñÿ òî÷êå.
Òàêèì îáðàçîì, ïîëèíîì f(x) = 0,071 + 0,518õ èç âñåõ ïîëèíîìîâ
ïåðâîé ñòåïåíè äåéñòâèòåëüíî ìèíèìèçèðóåò àáñîëþòíóþ âåëè÷èíó
îòêëîíåíèÿ îò ôóíêöèè 1%e
x
â èíòåðâàëå 0 x 1,5.
 òåîðèè àïïðîêñèìàöèè ôóíêöèé äîêàçûâàåòñÿ, ÷òî íàèáîëü-
øåå ïî àáñîëþòíîé âåëè÷èíå îòêëîíåíèå ïîëèíîìà f(õ) ñòåïåíè ï
îò íåïðåðûâíîé ôóíêöèè x(x) áóäåò ìèíèìàëüíî âîçìîæíûì, åñëè
â èíòåðâàëå ïðèáëèæåíèÿ à õ b ðàçíîñòü f(õ)%x(x) íå ìåíü-
øå, ÷åì ï + 2 ðàçà ïðèíèìàåò ñâîè ïîñëåäîâàòåëüíî ÷åðåäóþùèåñÿ
0
fx
()
-
x
1
1,5
-0,02
-0,01
0,5
0,01
x
()
x
0
fx
()
x
1
1,5
0,1
0,2
0,3
0,5
0,4
0,5
0,6
0,7
0,8
0,9
1
x
()
x
fx
()
x
()
x
Ðèñ. 10.26 Ðèñ. 10.27
249
ïðåäåëüíûå íàèáîëüøèå f(õ)%x(x) =
= L > 0 è íàèìåíüøèå f(õ)%x(x) =
= $L çíà÷åíèÿ (êðèòåðèé ×åáûøåâà).
Õàðàêòåð ãðàôèêà ðàçíîñòè
f(õ)%x(x) äëÿ ïîëèíîìà f(õ) ïÿòîé
ñòåïåíè, óäîâëåòâîðÿþùåãî ýòîìó
êðèòåðèþ, ïðèâåäåí íà ðèñ. 10.28.
Ýòîìó æå êðèòåðèþ óäîâëåòâîðÿåò
ïîëèíîì f(õ) â ðàññìîòðåííîì âûøå ïðèìåðå (ñì. ðèñ. 10.27).
Âî ìíîãèõ ïðèêëàäíûõ çàäà÷àõ íàõîäèò ïðèìåíåíèå ïîëèíîìè-
àëüíàÿ àïïðîêñèìàöèÿ ïî ñðåäíåêâàäðàòè÷åñêîìó êðèòåðèþ áëèçî-
ñòè, êîãäà ïàðàìåòðû àïïðîêñèìèðóþùåé ôóíêöèè f(õ) âûáèðàþò-
ñÿ èç óñëîâèÿ îáðàùåíèÿ â ìèíèìóì â èíòåðâàëå àïïðîêñèìàöèè
à õ b êâàäðàòà îòêëîíåíèÿ ôóíêöèè f(õ) îò çàäàííîé íåïðå-
ðûâíîé ôóíêöèè x(õ), ò. å., èç óñëîâèÿ:
( ) ( )
2
1
min
b
a
fxxdx
ba
L=-x=
-
ò
. (10.8)
 ñîîòâåòñòâèè ñ ïðàâèëàìè îòûñêàíèÿ ýêñòðåìóìîâ ðåøåíèå
çàäà÷è ñâîäèòñÿ ê ðåøåíèþ ñèñòåìû ëèíåéíûõ óðàâíåíèè, êîòîðàÿ
îáðàçóåòñÿ â ðåçóëüòàòå ïðèðàâíèâàíèÿ ê íóëþ ïåðâûõ ÷àñòíûõ
ïðîèçâîäíûõ ôóíêöèè L ïî êàæäîìó èç èñêîìûõ êîýôôèöèåíòîâ
à
k
àïïðîêñèìèðóþùåãî ïîëèíîìà f(x), ò. å. óðàâíåíèé
012
0;0;0,,0.
n
aaaa
¶L¶L¶L¶L
====
¶¶¶¶
K (10.9)
Äîêàçàíî, ÷òî è ýòà ñèñòåìà óðàâíåíèé èìååò åäèíñòâåííîå ðå-
øåíèå.  ïðîñòåéøèõ ñëó÷àÿõ îíî íàõîäèòñÿ àíàëèòè÷åñêè, à â
îáùåì ñëó÷àå $ ÷èñëåííî. Òàê, â ðàññìàòðèâàåìîì ïðèìåðå ñèñòå-
ìà óðàâíåíèé ïðè àïïðîêñèìàöèè â èíòåðâàëå 0 x l,5 ôóíêöèè
1
-
e
-
x
ïîëèíîìîì ïåðâîé ñòåïåíè òàêîâà:
( )
( )
1,5
01
0
0
1,5
01
1
0
210,
210,
x
x
aaxedx
a
aaxexdx
a
-
-
¶L
=+-+=
¶
¶L
=+-+=
¶
ò
ò
èëè ïîñëå ïðåîáðàçîâàíèé:
1,51,5
0101
32,2512;2,252,250,255.
aaeaae
--
+=+×+=-×
Ïîýòîìó f(õ) = 0,108 + 0,500x.
Çàìåòèì, ÷òî, êàê ïðàâèëî, ñðåäíÿÿ êâàäðàòè÷åñêàÿ ïîãðåø-
íîñòü íàèëó÷øåãî ðàâíîìåðíîãî ïðèáëèæåíèÿ ôóíêöèé f(õ) è x(õ)
ëèøü íå íàìíîãî îòëè÷àåòñÿ îò ìèíèìàëüíî âîçìîæíîé. Îáðàòíîå
óòâåðæäåíèå îáû÷íî îøèáî÷íî, ò. å. ïðè êâàäðàòè÷åñêîé àïïðîê-
ñèìàöèè â íåêîòîðûõ ó÷àñòêàõ èíòåðâàëà àïïðîêñèìàöèè âîçìîæ-
0
fx
()
-
x
b
-L
à
L
x
()
x
Ðèñ. 10.28

250
íû ñóùåñòâåííûå ïðåâûøåíèÿ ïî-
ãðåøíîñòè àïïðîêñèìàöèè (âûáðîñû)
ïî ñðàâíåíèþ ñ òåìè, êîòîðûå ñîîò-
âåòñòâóþò êðèòåðèþ (10.7).
Âåðíåìñÿ ê âîëüò-àìïåðíûì õà-
ðàêòåðèñòèêàì. Îáùèé âèä çàïèñè
ñòåïåííîãî ïîëèíîìà, àïïðîêñèìè-
ðóþùåãî ÂÀÕ:
2
012
.
n
n
iaauauau
=++++
K
(10.10)
Èíîãäà áûâàåò óäîáíî ðåøàòü çà-
äà÷ó àïïðîêñèìàöèè çàäàííîé õàðàêòåðèñòèêè â îêðåñòíîñòè ðàáî-
÷åé òî÷êè U
0
. Òîãäà èñïîëüçóþò ñòåïåííîé ïîëèíîì äðóãîãî âèäà:
( ) ( ) ( )
2
010200
.
n
n
iaauUauUauU=+-+-++-
K
(10.11)
Ïðèìåð. Èñïîëüçóÿ ìåòîä èíòåðïîëÿöèè, àïïðîêñèìèðîâàòü ÂÀÕ íåëè-
íåéíîãî ðåçèñòèâíîãî ýëåìåíòà (ðèñ. 10.29) ñòåïåííûì ïîëèíîìîì. Àïïðîêñè-
ìèðîâàííàÿ ÂÀÕ äîëæíà ñîâïàäàòü ñ çàäàííîé â âûáðàííûõ òî÷êàõ U
0
, U
1
è
U
2
.
Ñîñòàâèì ñèñòåìó óðàâíåíèé:
( ) ( )
( ) ( )
( ) ( )
2
00100200
2
10110210
2
20120221
IaaUUaUU
IaaUUaUU
IaaUUaUU
ì
=+-+-
ï
ï
=+-+-
í
ï
=+-+-
ï
î
èç êîòîðîé íàéä¸ì èñêîìûå êîýôôèöèåíòû
00
;
ai
=
( )
( ) ( ) ( )
2
222
01020120210
1
;
IUUUUIUUIUU
a
D
éù
---+---
ëû
=
(
)
(
)
(
)
021120201
2
;
IUUIUUIUU
a
D
-----
=
(
)
(
)
(
)
202101
DUUUUUU.
=----
Ïðèìåð. ÂÀÕ íåëèíåéíîãî ðåçèñòèâíîãî ýëåìåíòà i = F(u) çàäàíà òàáëè-
öåé:
u
k
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
i
k
0 0.06 0.23 0.5 0.85 1.18 1.65 2.3 2.9
Èñïîëüçóÿ êâàäðàòè÷åñêèé êðèòåðèé, àïïðîêñèìèðîâàòü õàðàêòåðèñòèêó
âûðàæåíèåì
2
2
iau
= .
Ñóììà êâàäðàòîâ îòêëîíåíèé àïïðîêñèìèðóþùåé ôóíêöèè îò çàäàííîé:
8
2
2
2
0
kk
k
aui
=
éù
L=-
ëû
å
ìèíèìàëüíà ïðè çíà÷åíèè êîýôôèöèåíòà a
2
, óäîâëåòâî-
ðÿþùåãî óðàâíåíèþ
0
i
u
I
2
I
0
I
1
U
1
U
0
U
2
Ðèñ. 10.29
