Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.


191
( ) ( ) ( )
( )
-t
=-=
-
t
12
1
.
1
p
FFF
ppp
e
p
Óñòðåìèâ t ® 0, íàéäåì èçîáðàæåíèå åäèíè÷íîé èìïóëüñíîé
ôóíêöèè (d-ôóíêöèè):
(
)
1.
t
d
Ýêñïîíåíöèàëüíûé ñèãíàë
()
t
fe
t
-a
= ïðè t > 0:
( )
0
1
,
tpt
Feedt
p
p
¥
-a-
==
a+
ò
ò. å.
( )
1.
t
e
p
-a
a+
(7.24)
Ïîäîáíûì æå îáðàçîì ìîæíî íàéòè èçîáðàæåíèå ïî Ëàïëàñó
äðóãèõ ôóíêöèé, óäîâëåòâîðÿþùèõ óñëîâèþ (7.3). Â ëèòåðàòóðå
èìåþòñÿ ñïåöèàëüíûå ñïðàâî÷íèêè, â êîòîðûõ ïðèâåäåíû îðèãè-
íàëû è èçîáðàæåíèÿ øèðîêîãî êëàññà ôóíêöèé. Â òàáë. 7.1 ïðè-
âåäåíû îðèãèíàëû è èõ èçîáðàæåíèÿ íàèáîëåå ÷àñòî âñòðå÷àþ-
ùèõñÿ â òåîðèè ýëåêòðè÷åñêèõ öåïåé ôóíêöèé.
7.2. Òåîðåìà ðàçëîæåíèÿ
Äëÿ íàõîæäåíèÿ îðèãèíàëà ïî èçîáðàæåíèþ ìîæíî âîñïîëü-
çîâàòüñÿ ëèáî òàáëèöàìè, ëèáî èñïîëüçîâàòü îáðàòíîå ïðåîáðàçî-
âàíèå Ëàïëàñà (7.4). Îäíàêî âû÷èñëåíèå îðèãèíàëà ñ ïîìîùüþ
(7.4) îáû÷íî îêàçûâàåòñÿ âåñüìà ñëîæíûì. Ïîýòîìó, äëÿ óïðî-
ùåíèÿ ðàñ÷åòîâ ïðèìåíÿþò òåîðåìó ðàçëîæåíèÿ, êîòîðàÿ ïîçâîëÿåò
ïðè íàõîæäåíèè îðèãèíàëà çàìåíèòü îïåðàöèþ èíòåãðèðîâàíèÿ â
(7.4) îïåðàöèåé ñóììèðîâàíèÿ, ÷òî çíà÷èòåëüíî óïðîùàåò âû-
÷èñëåíèÿ. Íàèáîëåå ñòðîãèé âûâîä ýòîé òåîðåìû ìîæíî îñóùåñò-
âèòü íà îñíîâàíèè òåîðåìû âû÷åòîâ. Çäåñü ìû îãðàíè÷èìñÿ âû-
âîäîì ôîðìóë ðàçëîæåíèÿ ïðèìåíèòåëüíî ê èçîáðàæåíèþ, ïðåä-
ñòàâëÿþùåìó ñîáîé ðàöèîíàëüíóþ äðîáü:
( )
( )
( )
1
1
110
1
2
110
,
nn
nn
mm
mm
F
p
apapapa
F
p
F
p
bpbpbpb
-
-
-
-
++++
==
++++
K
K
(7.25)
ãäå
110110
,,,;,,,
nnmm
aaaabbbb
--
KK
% âåùåñòâåííûå êîýôôèöèåí-
òû, ïðè÷åì F
1
(p) è F
2
(p) íå èìåþò îáùèõ êîðíåé.
Äëÿ íàõîæäåíèÿ îðèãèíàëà f(t) ðàçëîæèì F(p) íà ïðîñòûå
äðîáè:
(
)
( )
1
1
2
,
m
k
k
k
F
A
p
Fpp
p
=
=
-
å
(7.26)
ãäå p
k
% ïðîñòûå êîðíè õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ
( )
1
2110
0.
mm
mm
Fbpbpbpb
p
-
-
=++++=
K
(7.27)
A
k
% êîýôôèöèåíòû ðàçëîæåíèÿ.

192
Äëÿ òîãî, ÷òîáû íàéòè êîýôôèöèåíò A
k
äîìíîæèì îáå ÷àñòè
(7.26) íà (ð % p
k
) è ïåðåéäåì ê ïðåäåëó:
( )
(
)
( )
( )
1
1
2
limlim.
kk
m
k
kk
pppp
k
k
F
A
p
pppp
Fpp
p
®®
=
=
--
-
å
(7.28)
Ðàñêðûâàÿ íåîïðåäåëåííîñòü â ëåâîé ÷àñòè ðàâåíñòâà (7.28) ïî
ïðàâèëó Ëîïèòàëÿ è ó÷èòûâàÿ, ÷òî ñîãëàñíî (7.27) ïðàâàÿ ÷àñòü
(7.28) ðàâíà A
k
, ïîëó÷àåì
(
)
( )
( )
(
)
1
2
2
2
,
ãäå .
k
k
k
k
k
pp
F
p
dF
p
AF
p
dp
F
p
=
¢
==
¢
(7.29)
Ïîäñòàâèâ çíà÷åíèÿ A
k
â ôîðìóëó (7.26), íàéäåì:
( )
(
)
( )
(
)
( )
1
1
1
22
1
.
m
k
k
k
k
F
p
F
p
F
p
FFpp
p
p
=
==
¢
-
å
Åñëè ó÷åñòü, ÷òî èçîáðàæåíèå
( )
1
k
pt
k
e
pp-
(ñì. òàáë. 7.1), òî
íà îñíîâàíèè ñâîéñòâà ëèíåéíîñòè ïðåîáðàçîâàíèÿ Ëàïëàñà îêîí-
÷àòåëüíî ïîëó÷èì:
( )
(
)
( )
()
(
)
( )
1
1
1
22
.
k
m
pt
k
k
k
F
p
F
p
Ffe
p
t
FF
p
p
=
==
¢
å
(7.30)
Ôîðìóëà (7.30) ÿâëÿåòñÿ ìàòåìàòè÷åñêîé ôîðìóëèðîâêîé òåî-
ðåìû ðàçëîæåíèÿ è ïîçâîëÿåò íàéòè îðèãèíàë ïî èçîáðàæåíèþ â
âèäå (7.25), â ñëó÷àå ïðîñòûõ êîðíåé. Åñëè ñðåäè êîðíåé p
k
èìå-
åòñÿ îäèí íóëåâîé êîðåíü, ò. å. F
2
(ð) = pF
3
(p), òî òåîðåìà ðàçëî-
æåíèÿ ïðèìåò âèä
( )
(
)
( )
()
()
()
(
)
( )
1
1
1
1
333
0
.
0
k
m
pt
k
k
k
k
F
p
F
p
F
Ffe
p
t
pFFpF
p
p
=
==+
¢
å
(7.31)
Ôîðìóëó (7.31) ìîæíî ïîëó÷èòü, åñëè ïîäñòàâèòü â (7.30) âìåñòî
F
2
(ð) çíà÷åíèå pF
3
(ð) è îñóùåñòâèòü îïåðàöèþ äèôôåðåíöèðîâàíèÿ.
Åñëè ñðåäè êîðíåé óðàâíåíèÿ (7.27) (ïîëþñîâ ôóíêöèè F(p))
èìåþòñÿ êîìïëåêñíî-ñîïðÿæåííûå êîðíè p
k
è p
k+1
, òî â ôîðìóëå
(7.30) äîñòàòî÷íî âçÿòü p
k
, à äëÿ p
k+1
âçÿòü ñîïðÿæåííîå çíà÷åíèå,
ïðè ýòîì ñóììà ñîîòâåòñòâóþùàÿ äâóì ýòèì êîðíÿì ñ ó÷åòîì äåé-
ñòâèòåëüíîñòè f(t) áóäåò ðàâíà
(
)
( )
1
2
2Re.
k
k
pt
k
F
p
e
F
p
éù
êú
¢
ëû
(7.32)
Ïðè ýòîì â óðàâíåíèè äëÿ f(t) ïîÿâÿòñÿ ñîñòàâëÿþùèå òèïà (6.9):
( )
c
sin
t
Ae
t
-a
w+q
.
Òåîðåìó ðàçëîæåíèÿ ìîæíî îáîáùèòü è íà áîëåå îáùèå ñëó÷àè.
 ÷àñòíîñòè, åñëè ñðåäè ïîëþñîâ (7.25) èìåþòñÿ ïîëþñà êðàòíîñòè
l, òî â îðèãèíàëå f(t) ïîÿâÿòñÿ ñëàãàåìûå òèïà (6.8).

193
Ïðèìåð. Çàäàíî èçîáðàæåíèå â âèäå
( )
( )
2
2
54
p
F
p
p
pp
+
=
++
.
Îáîçíà÷èì F
1
(p) = p + 2; F
2
(p) = p(p
2
+ 5p + 4). Ïðè ýòîì ïîëó÷èì F(p) â
âèäå (7.25). Íàéäåì êîðíè õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ F
2
(p) = p(p
2
+
+ 5 p + 4) = 0.
123
0;1;4.
ppp
==-=-
Ïðè ýòîì F
1
(p
1
) = 2; F
1
(p
2
) = 1; F
1
(p
3
) = $2.
Îïðåäåëèì ïðîèçâîäíóþ
( )
2
2
3104.
Fpp
p
¢
=++
Îòñþäà F
2
¢(p
1
) = 4; F
2
¢(p
2
) = $3; F
2
¢(p
3
) = 12. Âîñïîëüçîâàâøèñü ôîðìó-
ëîé (7.30), îêîí÷àòåëüíî ïîëó÷èì:
( )
(
)
( )
(
)
( )
(
)
( )
1
11
34
12
3
12
222
3
12
111
.
236
pt
ptpt
tt
F
FF
p
pp
feeeee
t
FFF
p
pp
--
=++=--
¢¢¢
Ó÷èòûâàÿ, ÷òî ñðåäè êîðíåé õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ F
2
(p) = 0
èìååì îäèí íóëåâîé êîðåíü, ïðè íàõîæäåíèè f (t) ìîæíî áûëî âîñïîëüçîâàòü-
ñÿ è ôîðìóëîé (7.31). Äåéñòâèòåëüíî, åñëè îáîçíà÷èì
( )
2
3
54,
Fpp
p
=++
òî ïîëó÷èì
( )
(
)
( )
1
3
.
F
p
F
p
pF
p
=
Òîãäà êîðíè óðàâíåíèÿ F
3
(p) = 0 áóäóò ðàâíû p
1
= %l, p
2
=%4. Ñ ó÷åòîì
çíà÷åíèé
(
)
(
)
(
)
( ) ( )
( ) ( )
333
12
3111
12
25;3;3;
4;2;1;2
00
FpFF
pp
p
FFFF
pp
¢¢¢
=+==-
====-
ñîãëàñíî (7.31) îêîí÷àòåëüíî ïîëó÷èì
( )
( )
( )
(
)
( )
(
)
( )
11
12
4
1
12
31323
12
111
0
,
236
0
ptpt
tt
FF
pp
F
fee
ee
t
FpFpF
pp
--
æö
=++=
--
ç÷
¢¢
èø
÷òî ïîëíîñòüþ ñîâïàäàåò ñ ðàíåå ïîëó÷åííûì ðåøåíèåì.
7.3. Ðàñ÷åò ïåðåõîäíûõ ïðîöåññîâ îïåðàòîðíûì ìåòîäîì
Ïîëüçóÿñü îñíîâíûìè ñâîéñòâàìè ïðåîáðàçîâàíèÿ Ëàïëàñà,
ìîæíî ïîëó÷èòü îñíîâíûå çàêîíû òåîðèè öåïåé â îïåðàòîðíîé
ôîðìå. Ðàññìîòðèì, íàïðèìåð, ïîñëåäîâàòåëüíûé RLC-êîíòóð
(ñì. ðèñ. 6.14), íàõîäÿùèéñÿ ïðè íåíóëåâûõ íà÷àëüíûõ óñëîâèÿõ
u
C
(0
$
) ¹ 0; i
L
(0
$
) ¹ 0. Äëÿ ýòîãî êîíòóðà óðàâíåíèå ïî ÇÍÊ èìååò
âèä:
( )
0
11
.
0
tt
C
didi
uRiLidtRiLuidt
dtCdtC
-
-¥
=++=+++
òò
(7.33)

194
Ïðèìåíèâ ê (7.33) ïðÿìîå ïðåîáðàçîâàíèå Ëàïëàñà è ïðèíèìàÿ âî
âíèìàíèå ñâîéñòâà ëèíåéíîñòè, äèôôåðåíöèðîâàíèÿ è èíòåãðè-
ðîâàíèÿ îðèãèíàëà ïîëó÷èì:
( ) ( ) ( )
( )
(
)
( )
1
0
.
0
C
u
URIpLILiI
pppp
ppC
=+-++
Îòñþäà ïîëó÷àåì çàêîí Îìà â îïåðàòîðíîé ôîðìå äëÿ äàííîé
öåïè:
( )
(
)
(
)
(
)
(
)
( )
0
00
,
1
C
ULiupU
pp
I
p
RpLpCZ
p
+-
==
++
(7.34)
ãäå U
0
(p) = U(p) + Li (0) % u
C
(0)/p íîñèò íàçâàíèå îïåðàòîðíî-
ãî íàïðÿæåíèÿ; Z(p) = R + pL + 1/pC % îïåðàòîðíîãî ñîïðî-
òèâëåíèÿ öåïè. Åñëè â Z(p) çàìåíèòü ð íà jw, òî ïîëó÷èì êîì-
ïëåêñíîå ñîïðîòèâëåíèå öåïè. Âåëè÷èíû Li (0) è u
C
(0)/p íàçûâà-
þò ðàñ÷åòíûìè íàïðÿæåíèÿìè. Îíè õàðàêòåðèçóþò ýíåðãèþ ìàã-
íèòíîãî è ýëåêòðè÷åñêîãî ïîëåé, çàïàñåííóþ â L è Ñ ê ìîìåíòó
êîììóòàöèè. Âåëè÷èíà, îáðàòíàÿ Z(p) íàçûâàåòñÿ îïåðàòîðíîé
ïðîâîäèìîñòüþ öåïè:
( )
( )
11
.
1
Y
p
ZRpLpC
p
==
++
Äëÿ íóëåâûõ íà÷àëüíûõ óñëîâèé çàêîí Îìà ïðèìåò âèä
( )
(
)
( )
( ) ( )
.
U
p
IUY
ppp
Z
p
== (7.35)
Àíàëîãè÷íûì îáðàçîì ìîæíî ïîëó÷èòü çàêîíû Êèðõãîôà â îïå-
ðàòîðíîé ôîðìå:
ïåðâûé çàêîí (ÇÒÊ)
( )
1
0;
m
k
k
I
p
=
=
å
(7.36)
âòîðîé çàêîí (ÇÍÊ)
( )
1
0.
n
k
k
U
p
=
=
å
(7.37)
Òàêèì îáðàçîì, çàêîí Îìà è çàêîíû Êèðõãîôà â îïåðàòîðíîé
ôîðìå àíàëîãè÷íûì ýòèì æå çàêîíàì â êîìïëåêñíîé ôîðìå (ñì.
(3.48)%(3.50)) ñ òîé ëèøü ðàçíèöåé, ÷òî â (7.37) â êàæäîé èç ï
âåòâåé ïðè íàëè÷èè íåíóëåâûõ íà÷àëüíûõ óñëîâèé äåéñòâóþò äî-
ïîëíèòåëüíûå ðàñ÷åòíûå èñòî÷íèêè L
k
i
k
(0) è %u
Ck
(0)/ ð, ïîëîæè-
òåëüíîå íàïðàâëåíèå êîòîðûõ ñîâïàäàåò ñ âûáðàííûì ïîëîæè-
òåëüíûì íàïðàâëåíèåì òîêà â ýòîé âåòâè.
Èñïîëüçóÿ çàêîíû Îìà è Êèðõãîôà â îïåðàòîðíîé ôîðìå, ìîæ-
íî íàéòè èçîáðàæåíèÿ èñêîìûõ òîêîâ è íàïðÿæåíèé â öåïè. Äëÿ
îïðåäåëåíèÿ îðèãèíàëîâ òîêîâ è íàïðÿæåíèé ìîæíî âîñïîëüçî-
195
âàòüñÿ ëèáî òàáëèöàìè îðèãèíàëîâ è èçîáðàæåíèé, ëèáî ïðèìåíèòü
òåîðåìó ðàçëîæåíèÿ.
Äëÿ èëëþñòðàöèè îñíîâíûõ òåîðåòè÷åñêèõ ïîëîæåíèé íàéäåì
îïåðàòîðíûì ìåòîäîì çàêîí èçìåíåíèÿ òîêà â ïîñëåäîâàòåëüíîì
RLC-êîíòóðå ïðè âêëþ÷åíèè åãî íà èñòî÷íèê ïîñòîÿííîãî íàïðÿ-
æåíèÿ (ñì. § 6.5). Óðàâíåíèå äëÿ èçîáðàæåíèÿ òîêà ìîæíî íàéòè
ïî çàêîíó Îìà äëÿ íóëåâûõ íà÷àëüíûõ óñëîâèé (7.35) ñ ó÷åòîì
èçîáðàæåíèÿ ïîñòîÿííîãî íàïðÿæåíèÿ U(p)
U/p:
( )
(
)
( )
(
)
( )
1
2
2
.
1
1
UF
pp
UpCU
I
p
ZRpLpCF
pp
LCpRCp
====
++
++
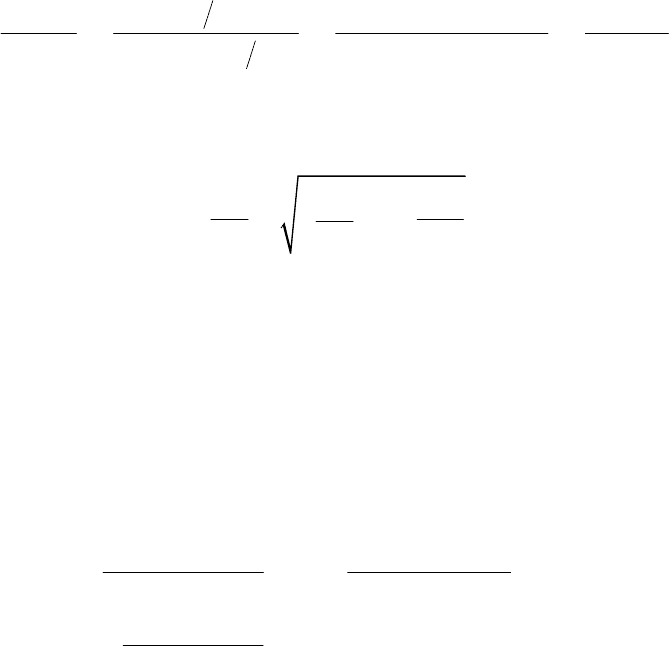
Íàéäåì êîðíè õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ
( )
2
2
2
1,2
10;
1
.
2
2
FLCpRCp
p
R
R
p
LLC
L
=++=
æö
=-±-
ç÷
èø
Ïðè R > 2r êîðíè áóäóò âåùåñòâåííû è ðàçëè÷íû. Äëÿ íàõîæäå-
íèÿ îðèãèíàëà òîêà i(t) âîñïîëüçóåìñÿ òåîðåìîé ðàçëîæåíèÿ
(7.30). Äëÿ ýòîãî íàéäåì ïðîèçâîäíûå F
2
¢(p
1
) è F
2
¢(p
2
):
(
)
( )
21
1
22
2
2;
2.
FLCpRC
p
FLCpRC
p
¢
=+
¢
=+
Ïîäñòàâèâ çíà÷åíèÿ F
1
(p) = F
1
(p
2
) = CU è F
2
¢(p
1
) è F
2
¢(p
2
) â
(7.30) ïîëó÷èì îðèãèíàë òîêà
( )
( )
( )
12
21
12
12
22
,
ptpt
ptpt
CUCU
iee
t
LCpRCLCpRC
U
ee
L
pp
=+
++
=-
-
-
÷òî ïîëíîñòüþ ñîâïàäàåò ñ ðàíåå ïîëó÷åííûì óðàâíåíèåì
(6.68).
Èç ðàññìîòðåííîãî ïðèìåðà õîðîøî âèäíû ïðåèìóùåñòâà îïå-
ðàòîðíîãî ìåòîäà: ïðîñòîòà, îòñóòñòâèå ãðîìîçäêèõ îïåðàöèé ïî
îïðåäåëåíèþ ïîñòîÿííûõ èíòåãðèðîâàíèÿ. Ñëåäóåò ïîä÷åðêíóòü,
÷òî áàçèðóÿñü íà çàêîíàõ Îìà è Êèðõãîôà â îïåðàòîðíîé ôîðìå,
ìîæíî ðàññ÷èòàòü ïåðåõîäíûé ïðîöåññ ëþáûì èç ðàíåå ðàññìîò-
ðåííûõ ìåòîäîâ: êîíòóðíûõ òîêîâ, óçëîâûõ íàïðÿæåíèé è äð.
Ïðè ýòîì óäîáíî ïîëüçîâàòüñÿ ýêâèâàëåíòíûìè îïåðàòîðíûìè
ñõåìàìè. Ïðè ñîñòàâëåíèè ýêâèâàëåíòíûõ îïåðàòîðíûõ ñõåì èñ-
òî÷íèêè òîêà è íàïðÿæåíèé i(t) è u(t) çàìåíÿþòñÿ ñîîòâåòñò-
âóþùèìè èçîáðàæåíèÿìè I(p) è U(p), èíäóêòèâíîñòü L çàìåíÿ-
åòñÿ íà pL, à åìêîñòü Ñ % íà 1/pC ïðè íóëåâûõ íà÷àëüíûõ óñ-
ëîâèÿõ. Åñëè íà÷àëüíûå óñëîâèÿ íåíóëåâûå, òî ïîñëåäîâàòåëüíî
ñ pL äîáàâëÿåòñÿ èñòî÷íèê íàïðÿæåíèÿ Li(0), à ñ Ñ % èñòî÷íèê

196
+
L
C
u
C
(0)
i
(0)
pL
Li
(0)
1/
pC
u
C
(0)/
p
+
+
R
1
R
2
u
C
(0)/
p
pL
1/
pC
U
/
p
I
3
()
p
I
1
()
p
I
2
()
p
+
Ðèñ. 7.5 Ðèñ. 7.6
íàïðÿæåíèÿ % u
C
(0)/ð (ðèñ. 7.5)
*
. Íàïðèìåð, ýêâèâàëåíòíàÿ
îïåðàòîðíàÿ ñõåìà äëÿ öåïè, èçîáðàæåííîé íà ðèñ. 6.17, áóäåò
èìåòü âèä (ðèñ. 7.6). Ñîñòàâèâ äëÿ ýòîé ñõåìû óðàâíåíèÿ ïî çà-
êîíàì Êèðõãîôà â îïåðàòîðíîé ôîðìå, ïîëó÷èì ñèñòåìó àëãåá-
ðàè÷åñêèõ óðàâíåíèé, ðåøåíèå êîòîðûõ ñóùåñòâåííî ïðîùå ñèñ-
òåìû (6.86).
Îïåðàòîðíûé ìåòîä ìîæíî èñïîëüçîâàòü è äëÿ ðåøåíèÿ óðàâíåíèÿ ñîñòîÿ-
íèÿ öåïè (ñì. § 6.7). Ïðè ýòîì óðàâíåíèå ñîñòîÿíèÿ (6.94) ñ ó÷åòîì ñâîéñòâ
äèôôåðåíöèðîâàíèÿ îðèãèíàëà è ëèíåéíîñòè ïðåîáðàçîâàíèÿ Ëàïëàñà ïðèìåò
âèä:
(
)
(
)
(
)
(
)
,
0
p
ppp
-=+
XxAXBW (7.38)
ãäå Õ(ð), W(p) % èçîáðàæåíèÿ âåêòîðîâ ñîñòîÿíèÿ x(t) è âõîäíûõ âîçäåéñò-
âèé W(t).
Èç (7,38) ïîëó÷àåì íåïîñðåäñòâåííî ðåøåíèå
( ) ( ) ( ) ( )
( )
11
,
0
pppp
--
=+
--
XBWx
IAIA
(7.39)
ãäå I % åäèíè÷íàÿ ìàòðèöà. Ïðèìåíèâ ê (7.39) òåîðåìó ðàçëîæåíèÿ, ìîæíî
ïîëó÷èòü èñêîìûé âåêòîð ñîñòîÿíèÿ
(
)
(
)
.
p
t
xX
7.4. Îïåðàòîðíûå ïåðåäàòî÷íûå ôóíêöèè
Âàæíóþ ðîëü â ìåòîäàõ àíàëèçà è ñèíòåçà ýëåêòðè÷åñêèõ öåïåé
ïðè íóëåâûõ íà÷àëüíûõ óñëîâèÿõ èãðàþò îïåðàòîðíûå ïåðå-
äàòî÷íûå ôóíêöèè, êîòîðûå îïðåäåëÿþòñÿ êàê îòíîøåíèå èçîáðà-
æåíèÿ âûõîäíîé ðåàêöèè öåïè ê èçîáðàæåíèþ âõîäíîãî âîçäåéñò-
âèÿ.  ñîîòâåòñòâèè ñ ýòèì îïðåäåëåíèåì ðàçëè÷àþò ÷åòûðå âèäà
ïåðåäàòî÷íûõ ôóíêöèé:
*
Âîçìîæíû ñõåìû çàìåùåíèÿ çàðÿæåííîé åìêîñòè u
C
(0) è èíäóêòèâíîñòè ñ òîêîì
i
L
(0) ñ ïîìîùüþ èñòî÷íèêîâ òîêà ñ çàäàþùèìè òîêàìè Cu
C
(0) è i
L
(0)/p ñî-
îòâåòñòâåííî.

197
( )
(
)
( )
( )
(
)
( )
( )
( )
( )
( )
( )
( )
22
11
22
11
,,
,.
ui
ZY
UI
pp
HH
pp
UI
pp
UI
pp
HH
pp
IU
pp
ü
==
ï
ï
ý
ï
==
ï
þ
(7.40)
ãäå Í
è
(ð), H
i
(p) èìåþò ñìûñë îïåðàòîðíûõ ïåðåäàòî÷íûõ ôóíê-
öèé ïî íàïðÿæåíèþ è òîêó; Í
L
(ð); Í
Y
(ð) %îïåðàòîðíûå ïåðåäà-
òî÷íûå ñîïðîòèâëåíèå è ïðîâîäèìîñòü ñîîòâåòñòâåííî.
Åñëè â (7.40) çàìåíèòü îïåðàòîð ð íà jw, òî ïîëó÷èì óðàâíåíèå
êîìïëåêñíûõ ïåðåäàòî÷íûõ ôóíêöèé Í(jw), êîòîðûå áûëè ðàñ-
ñìîòðåíû â § 4.1 è øèðîêî èñïîëüçóþòñÿ ïðè ÷àñòîòíûõ ìåòîäàõ
àíàëèçà ýëåêòðè÷åñêèõ öåïåé (ñì. § 4.2%4.4, 9.5).
Çíàÿ ïåðåäàòî÷íóþ ôóíêöèþ öåïè Í(ð), ñ ïîìîùüþ (7.40) íå-
òðóäíî íàéòè èçîáðàæåíèå ðåàêöèè öåïè, à ñëåäîâàòåëüíî, è ñàìó
ðåàêöèþ íà çàäàííîå âîçäåéñòâèå.
Îïåðàòîðíóþ ïåðåäàòî÷íóþ ôóíêöèþ Í(ð) äëÿ ïàññèâíîé öåïè
ìîæíî ïðåäñòàâèòü êàê äðîáíî-ðàöèîíàëüíóþ ôóíêöèþ ñ âåùåñò-
âåííûìè êîýôôèöèåíòàìè:
( )
( )
( )
1
110
1
110
;
nn
nn
mm
mm
w
p
apapapa
H
p
v
p
bpbpbpb
-
-
-
-
++++
==
++++
K
K
(7.41)
èëè â âèäå
( )
(
)
(
)
(
)
( )( )
( )
0020
12
,
n
m
pppppp
HH
p
pp
pppp
---
=
-
--
K
K
(7.42)
ãäå p
01
, p
02
, ..., p
0n
% íóëè; p
1
, p
2
, ..., p
m
% ïîëþñû ïåðåäàòî÷-
íîé ôóíêöèè; Í = à
n
/b
m
.
Ñòåïåíè ïîëèíîìîâ ÷èñëèòåëÿ ï è çíàìåíàòåëÿ ò çàâèñÿò îò
÷èñëà ðåàêòèâíûõ ýëåìåíòîâ ïàññèâíîé öåïè.
Çàìåíèâ â (7.41) îïåðàòîð ð íà jw, ïîëó÷èì êîìïëåêñíóþ ïå-
ðåäàòî÷íóþ ôóíêöèþ öåïè
( ) ( )
(
)
,
j
HHe
jj
jw
=
ww
ãäå À×Õ öåïè
( )
( ) ( )
( ) ( )
22
2435
024135
22
2435
024135
;
aaaaaa
H
j
bbbbbb
+
-w+w-w-w+w-
=
w
+
-w+w-w-w+w-
KK
KK
(7.43)
Ô×Õ öåïè
( )
(
)
( )
( )
( )
35
135
24
024
35
135
24
024
arctg
arctg.
aaa
aaa
bbb
bbb
w-w+w-
jw=-
-w+w-
w-w+w-
-
-w+w-
K
K
K
K
(7.44)

198
Ó÷èòûâàÿ, ÷òî ñîãëàñíî (7.43) | H(jw)| ÿâëÿåòñÿ èððàöèîíàëü-
íîé, îáû÷íî ïðè àíàëèçå è ñèíòåçå öåïåé èìåþò äåëî ñ êâàäðàòîì
À×Õ:
( )
2222
2
011
2222
011
,
nn
nn
mm
mm
cccc
H
j
dddd
-
-
-
-
w+w++w+
=
w
w+w++w+
K
K
(7.45)
ãäå êîýôôèöèåíòû ñ
k
è d
k
ïîëó÷àþòñÿ ïóòåì îáúåäèíåíèÿ êîýô-
ôèöèåíòîâ ïðè îäèíàêîâûõ ñòåïåíÿõ ïåðåìåííîé w.
Ïåðå÷èñëèì îñíîâíûå ñâîéñòâà îïåðàòîðíûõ ïåðåäàòî÷íûõ
ôóíêöèé è êâàäðàòà À×Õ ïàññèâíûõ öåïåé:
1. Ïåðåäàòî÷íàÿ ôóíêöèÿ ÿâëÿåòñÿ äðîáíî-ðàöèîíàëüíîé ôóíê-
öèåé ñ âåùåñòâåííûìè êîýôôèöèåíòàìè. Âåùåñòâåííîñòü êîýôôè-
öèåíòîâ îáúÿñíÿåòñÿ òåì, ÷òî îíè îïðåäåëÿþòñÿ ýëåìåíòàìè ñõåìû.
2. Ïîëþñû ïåðåäàòî÷íîé ôóíêöèè ðàñïîëàãàþòñÿ â ëåâîé ïî-
ëóïëîñêîñòè êîìïëåêñíîé ïåðåìåííîé ð. Íà ðàñïîëîæåíèå íóëåé
îãðàíè÷åíèé íåò. Äîêàæåì ýòî ñâîéñòâî íà ïðèìåðå ïåðåäàòî÷íîé
ôóíêöèè Í
è
(ð) = U
2
(ð)/U
1
(ð). Âûáåðåì âõîäíîå âîçäåéñòâèå
u
1
(t) = d(t) èëè â îïåðàòîðíîé ôîðìå U(ð) = l. Èçîáðàæåíèå âû-
õîäíîãî íàïðÿæåíèÿ U
2
(ð) = U
1
(ð)Í
è
(ð) â ýòîì ñëó÷àå ÷èñëåííî
ðàâíî Í
è
(ð), ò. å.
( ) ( )
(
)
( )
( )( )
( )
2
1
110
12
12
12
,
u
mm
m
m
m
m
w
p
UH
pp
pbpbpb
w
p
A
AA
pppppp
pp
pppp
-
-
===
++++
==+++
---
-
--
K
K
K
ãäå w(p) % ïîëèíîì ÷èñëèòåëÿ ïåðåäàòî÷íîé ôóíêöèè; A
1
, A
2
, ...,
A
m
, %êîýôôèöèåíòû ðàçëîæåíèÿ äðîáíî-ðàöèîíàëüíîé ôóíêöèè
íà ñóììó ïðîñòûõ äðîáåé.
Ïåðåéäåì îò èçîáðàæåíèÿ U
2
(p) ê îðèãèíàëó u
2
(t):
()
12
212
,
m
ptpt
pt
m
uAeAeAe
t
=+++
K
(7.46)
ãäå â îáùåì ñëó÷àå p
i
= a
i
+ jw
i
.
 ïàññèâíûõ è óñòîé÷èâûõ àêòèâíûõ ÷åòûðåõïîëþñíèêàõ êîëå-
áàíèÿ íà âûõîäå ÷åòûðåõïîëþñíèêà ïîñëå ïðåêðàùåíèÿ âîçäåé-
ñòâèÿ äîëæíû èìåòü çàòóõàþùèé õàðàêòåð. Ýòî îçíà÷àåò, ÷òî â
(7.46) âåùåñòâåííûå ÷àñòè ïîëþñîâ p
i
äîëæíû áûòü îòðèöàòåëü-
íûìè (a
i
< 0), ò. å. ïîëþñû äîëæíû íàõîäèòüñÿ â ëåâîé ïîëóïëî-
ñêîñòè ïåðåìåííîé ð.
3. Ñòåïåíè ïîëèíîìîâ ÷èñëèòåëåé ïåðåäàòî÷íîé ôóíêöèè è
êâàäðàòà À×Õ íå ïðåâûøàþò ñòåïåíåé ïîëèíîìîâ çíàìåíàòåëåé,
ò. å. ï < ò. Åñëè áû ýòî ñâîéñòâî íå âûïîëíÿëîñü, òî íà áåñêîíå÷-
íî áîëüøèõ ÷àñòîòàõ À×Õ ïðèíèìàëà áû áåñêîíå÷íî áîëüøîå çíà-
÷åíèå (òàê êàê ÷èñëèòåëü ðîñ áû ñ óâåëè÷åíèåì ÷àñòîòû áûñòðåå
çíàìåíàòåëÿ), ò. å. öåïü îáëàäàëà áû áåñêîíå÷íûì óñèëåíèåì, ÷òî
ïðîòèâîðå÷èò ôèçè÷åñêîìó ñìûñëó.

199
R
1
R
2
C
U
R
1
R
2
C
i
2
i
3
R
3
i
1
E
R
R
L
Ðèñ. 7.7 Ðèñ. 7.8 Ðèñ. 7.9
4. Êâàäðàò À×Õ ÿâëÿåòñÿ ÷åòíîé ðàöèîíàëüíîé ôóíêöèåé ïåðå-
ìåííîé w ñ âåùåñòâåííûìè êîýôôèöèåíòàìè. Ýòî ñâîéñòâî ñ î÷å-
âèäíîñòüþ âûòåêàåò èç ñïîñîáà ïîëó÷åíèÿ êâàäðàòà À×Õ ïî ïåðå-
äàòî÷íîé ôóíêöèè.
5. Êâàäðàò À×Õ íå ìîæåò ïðèíèìàòü îòðèöàòåëüíûõ è áåñêî-
íå÷íî áîëüøèõ çíà÷åíèé ïðè w > 0. Íåîòðèöàòåëüíîñòü
(
)
2
j
H
w
ñëåäóåò èç ñâîéñòâ êâàäðàòà ìîäóëÿ êîìïëåêñíîé âåëè÷èíû. Êî-
íå÷íîñòü çíà÷åíèé À×Õ íà ðåàëüíûõ ÷àñòîòàõ îáúÿñíÿåòñÿ òàê æå,
êàê è â ñâîéñòâå 3.
Âîïðîñû è çàäàíèÿ äëÿ ñàìîïðîâåðêè
1.  ÷åì çàêëþ÷àåòñÿ ñóùíîñòü îïåðàòîðíîãî ìåòîäà ðàñ÷åòà öåïè?
2. ×òî òàêîå îïåðàòîðíîå ñîïðîòèâëåíèå öåïè?
3. ×òî òàêîå îïåðàòîðíûå ñõåìû çàìåùåíèÿ ïðè ñîñòàâëåíèè ýêâè-
âàëåíòíîé îïåðàòîðíîé ñõåìû?
4. ×åì çàìåíÿþòñÿ èíäóêòèâíîñòè è åìêîñòè â îïåðàòîðíîé ñõåìå
çàìåùåíèÿ?
5. Êàê ó÷èòûâàþòñÿ íåçàâèñèìûå íà÷àëüíûå óñëîâèÿ?
6. Çàïèñàòü çàêîí Îìà è çàêîíû Êèðõãîôà â îïåðàòîðíîé ôîðìå.
7. ×òî òàêîå åäèíè÷íàÿ ôóíêöèÿ è d-ôóíêöèÿ?
8. ×òî ïîíèìàåòñÿ ïîä îïåðàòîðíîé ïåðåäàòî÷íîé ôóíêöèåé? Êà-
êîâû åå ñâîéñòâà?
9. Êàêèì îáðàçîì ìîæíî ïåðåéòè îò èçîáðàæåíèÿ ê îðèãèíàëó?
10. Äëÿ ñõåìû, èçîáðàæåííîé íà ðèñ. 7.7, îïåðàòîðíûì ìåòîäîì
îïðåäåëèòü íàïðÿæåíèå íà êîíäåíñàòîðå u
C
(t). U = 20 Â; R
1
=
= R
2
= 100 Îì; Ñ = 4 ìêÔ.
Îòâåò: u
C
(t) = 10 $
3
510
10
t
e
-
×
, Â.
11. Äëÿ ñõåìû, èçîáðàæåííîé íà ðèñ. 7.8, íàéòè èçîáðàæåíèå òîêà
I
2
(p).
Îòâåò: I
2
(p) =
( )
3
3
1,675105
210
p
p
p
-
×+
+×
.
12. Çíàÿ èçîáðàæåíèå òîêà (ðèñ. 7.8), îïðåäåëèòü îðèãèíàë i
2
(t).
Îòâåò: i
2
(t) = 2,5 $ 0,825
3
210
t
e
-×
.

200
13. Äëÿ ñõåìû, èçîáðàæåííîé íà ðèñ. 7.9, îïðåäåëèòü:
1) îïåðàòîðíóþ ïåðåäàòî÷íóþ ôóíêöèþ H
u
(p);
2) íàéòè À×Õ öåïè.
Îòâåò:
( )
;
2
u
R
H
p
RpL
=
+
( )
222
.
4
R
H
RL
w=
+w
ÃËÀÂÀ 8. ÂÐÅÌÅÍÍÎÉ ÌÅÒÎÄ ÀÍÀËÈÇÀ ÏÅÐÅÕÎÄÍÛÕ
ÏÐÎÖÅÑÑΠ ËÈÍÅÉÍÛÕ ÝËÅÊÒÐÈ×ÅÑÊÈÕ ÖÅÏßÕ
8.1. Ïåðåõîäíûå è èìïóëüñíûå õàðàêòåðèñòèêè
ýëåêòðè÷åñêèõ öåïåé
 îñíîâå âðåìåííîãî ìåòîäà ëåæèò ïîíÿòèå ïåðåõîäíîé è èì-
ïóëüñíîé õàðàêòåðèñòèê öåïè. Ïåðåõîäíîé õàðàêòåðèñòèêîé öåïè
íàçûâàþò ðåàêöèþ öåïè íà âîçäåéñòâèå â ôîðìå åäèíè÷íîé ôóíê-
öèè (7.19). Îáîçíà÷àåòñÿ ïåðåõîäíàÿ õàðàêòåðèñòèêà öåïè g(t).
Èìïóëüñíîé õàðàêòåðèñòèêîé öåïè íàçûâàþò ðåàêöèþ öåïè íà
âîçäåéñòâèå åäèíè÷íîé èìïóëüñíîé ôóíêöèè (d-ôóíêöèè) (7.21).
Îáîçíà÷àåòñÿ èìïóëüñíàÿ õàðàêòåðèñòèêà h (t). Ïðè÷åì, g(t) è
h(t) îïðåäåëÿþòñÿ ïðè íóëåâûõ íà÷àëüíûõ óñëîâèÿõ â öåïè
*
. Â
çàâèñèìîñòè îò òèïà ðåàêöèè è òèïà âîçäåéñòâèÿ (òîê èëè íàïðÿ-
æåíèå) ïåðåõîäíûå è èìïóëüñíûå õàðàêòåðèñòèêè ìîãóò áûòü áåç-
ðàçìåðíûìè âåëè÷èíàìè, ëèáî èìåþò ðàçìåðíîñòü À/ èëè Â/À.
Èñïîëüçîâàíèå ïîíÿòèé ïåðåõîäíîé è èìïóëüñíîé õàðàêòåðè-
ñòèê öåïè ïîçâîëÿåò ñâåñòè ðàñ÷åò ðåàêöèè öåïè îò äåéñòâèÿ íåïå-
ðèîäè÷åñêîãî ñèãíàëà ïðîèçâîëüíîé ôîðìû ê îïðåäåëåíèþ ðåàêöèè
öåïè íà ïðîñòåéøåå âîçäåéñòâèå òèïà åäèíè÷íîé 1(t) èëè èìïóëüñ-
íîé ôóíêöèè d(t), ñ ïîìîùüþ êîòîðûõ àïïðîêñèìèðóåòñÿ èñõîä-
íûé ñèãíàë. Ïðè ýòîì ðåçóëüòèðóþùàÿ ðåàêöèÿ ëèíåéíîé öåïè íà-
õîäèòñÿ (ñ èñïîëüçîâàíèåì ïðèíöèïà íàëîæåíèÿ) êàê ñóììà ðåàê-
öèé öåïè íà ýëåìåíòàðíûå âîçäåéñòâèÿ 1(t) èëè d(t).
Ìåæäó ïåðåõîäíîé g(t) è èìïóëüñíîé h (t) õàðàêòåðèñòèêàìè
ëèíåéíîé ïàññèâíîé öåïè ñóùåñòâóåò îïðåäåëåííàÿ ñâÿçü. Åå ìîæ-
íî óñòàíîâèòü, åñëè ïðåäñòàâèòü åäèíè÷íóþ èìïóëüñíóþ ôóíêöèþ
÷åðåç ïðåäåëüíûé ïåðåõîä ðàçíîñòè äâóõ åäèíè÷íûõ ôóíêöèé âå-
ëè÷èíû 1/t, ñäâèíóòûõ äðóã îòíîñèòåëüíî äðóãà íà âðåìÿ t (ñì.
ðèñ. 7.4):
()
(
)
(
)
() ()
0
11
lim11,
d
tt
ttt
dt
t®
-
-t
¢
d===
t
(8.1)
*
Èìïóëüñíûå è ïåðåõîäíûå õàðàêòåðèñòèêè öåïåé îòíîñÿòñÿ ê òàê íàçûâàåìûì íîð-
ìèðîâàííûì âðåìåííûì õàðàêòåðèñòèêàì, ïîñêîëüêó îíè ðàññìàòðèâàþòñÿ ïî îò-
íîøåíèþ ê åäèíè÷íîé ïëîùàäè èìïóëüñíîãî âîçäåéñòâèÿ èëè åäèíè÷íîãî ñêà÷êà.
