Бакалов В.П. Основы теории цепей. 3-е издание

Подождите немного. Документ загружается.

181

( )

[ ]

( )

[ ]

( )

eed

=+tt

xxBw (6.98)

Èíòåãðàë â (6.98) âû÷èñëÿåòñÿ ÷èñëåííûìè ìåòîäàìè (ìåòîäîì

ïðÿìîóãîëüíèêîâ, òðàïåöèé, Ñèìïñîíà è äð.). Òàê, ïðè èñïîëüçî-

âàíèè ìåòîäà ïðÿìîóãîëüíèêîâ àëãîðèòì (6.98) ïðèîáðåòàåò âèä

( )

[

]

(

)

(

)

eehnh

xxBw (6.99)

Ïðè íóëåâîì âõîäíîì ñèãíàëå w = 0 (ñâîáîäíûå êîëåáàíèÿ)

( )

[

]

(

)

xx (6.100)

Åñëè îãðàíè÷èòüñÿ â ðàçëîæåíèè (6.97) òîëüêî ïåðâûìè äâóìÿ

÷ëåíàìè e

» I + Ah, òî ïîëó÷èì

( )

[

]

(

)

(

)

nhnh

»+

xxAx (6.101)

Àëãîðèòì (6.101) ëåãêî ïðîãðàììèðóåòñÿ íà ÝÂÌ è èìååò ÿñ-

íûé ôèçè÷åñêèé ñìûñë. Îí îïðåäåëÿåò ïîëîæåíèå òî÷êè â ïðî-

ñòðàíñòâå ñîñòîÿíèé íà (n + 1)-ì øàãå, èñõîäÿ èç åå ñîñòîÿíèÿ íà

n-ì øàãå ïðè àïïðîêñèìàöèè òðàåêòîðèè íà ó÷àñòêå h ïðÿìîëè-

íåéíûì îòðåçêîì ñ ïîñòîÿííîé ñêîðîñòüþ

(h).

Ïðèìåð. Ðàññ÷èòàòü òðàåêòîðèþ ñîñòîÿíèé, èçîáðàæåííóþ íà ðèñ. 6.19,

èñïîëüçóÿ àïïðîêñèìàöèþ åå íà êàæäîì èç m ó÷àñòêîâ âåëè÷èíû h â ôîðìå

ïðÿìîëèíåéíûõ îòðåçêîâ. Ñêîðîñòü èçìåíåíèÿ ñîñòîÿíèÿ

(h) íà êàæäîì èç

âûäåëåííûõ ó÷àñòêîâ îñòàåòñÿ ïîñòîÿííîé.

Íà îñíîâàíèè óðàâíåíèÿ ñîñòîÿíèÿ (6.93) èìååì:

äëÿ ìîìåíòà t = 0;

(0) = Àõ(0);

äëÿ ìîìåíòà t = h

(

)

(

)

(

)

(

)

(

)

;

0000

»+=+

xxxxAx

äëÿ ìîìåíòà t = 2h

(

)

(

)

(

)

(

)

(

)

;

hhhhh

»+=+

xxxxAx

äëÿ ìîìåíòà t = (n + 1)h

( )

[

]

(

)

(

)

nhnh

»+

xxAx

ò. å. ïîëó÷åííîå óðàâíåíèå ïîëíîñòüþ ñîâïàäàåò ñ (6.101).

Ìåòîä Ðóíãå$Êóòòà % ìåòîä ÷èñëåííîãî ðåøåíèÿ óðàâíåíèÿ

ñîñòîÿíèÿ (6.94), ïðè êîòîðîì èíòåðâàë 0...t ðàçáèâàåòñÿ íà ò ìà-

ëûõ ó÷àñòêîâ Dt = h, íà êàæäîì èç êîòîðûõ çíà÷åíèå ïåðåìåííîé

õ îïðåäåëÿåòñÿ ñ ïîìîùüþ ëèíåéíîé êîìáèíàöèè íåêîòîðûõ âñïî-

ìîãàòåëüíûõ ôóíêöèé k

(h) ñ ïîñòîÿííûìè êîýôôèöèåíòàìè. Â

çàâèñèìîñòè îò ñïîñîáà âûáîðà êîýôôèöèåíòîâ è òðåáóåìîé òî÷-

íîñòè ðåøåíèÿ ñóùåñòâóþò ðàçëè÷íûå ìîäèôèêàöèè àëãîðèòìîâ

Ðóíãå%Êóòòà.

182

Ïðîèëëþñòðèðóåì ñóòü ìåòîäà Ðóíãå%Êóòòà íà ïðèìåðå ñêà-

ëÿðíîãî óðàâíåíèÿ ñîñòîÿíèÿ

( )

(6.102)

Íàèáîëåå ðàñïðîñòðàíåííûé àëãîðèòì Ðóíãå%Êóòòà èìååò âèä

( )

( ) ( )

1234

001

002003

ãäå;;

2;2

2;2;

kkkk

khfkhf

thxk

khfkhf

thxkthxk

»+

+++

++++

(6.103)

Ïðè ýòîì ïîðÿäîê ïîãðåøíîñòè ñîñòàâëÿåò h

Ïðèìåð. Ðåøèòü ñêàëÿðíîå óðàâíåíèå ñîñòîÿíèÿ (6.102) íà èíòåðâàëå

[0; t] ìåòîäîì Ðóíãå%Êóòòà ïðè óñëîâèè A = 1; õ(0) = 1.

Ð å ø å í è å. Ðàçîáüåì èíòåðâàë [0; t] íà 10 ó÷àñòêîâ ñ øàãîì h = 0,1.

Òîãäà â ñîîòâåòñòâèè ñ àëãîðèòìàìè (6.103) ìîæåì ïîëó÷èòü äëÿ t = 0,

õ(0) = 1 (ïåðâûé øàã):

( )

[

]

( )

[ ]

( )

[ ]

( )

1234

0,1;0,105;

0,10525;0,110525;

1161,105174.

0,10,210,21050,110525

khxkh

khkh

kkkk

====

=+=

+++

=+=

+++

Àíàëîãè÷íî íà âòîðîì øàãå

(

)

( )

1234

1,105174161,121140

è ò. ä.

0,10520,11620,11630,122

kkkk

=+=

+++

=+=

+×+×+

Êàê ñëåäóåò èç (6.103), äëÿ îïðåäåëåíèÿ õ íåîáõîäèìî âû÷èñëèòü f (t, x) â

÷åòûðåõ òî÷êàõ.

Àíàëîãè÷íî çàïèñûâàåòñÿ àëãîðèòì Ðóíãå%Êóòòà äëÿ ñèñòåìû

óðàâíåíèé òèïà (6.102). Íàïðèìåð, äëÿ ñëó÷àÿ ñèñòåìû èç äâóõ

óðàâíåíèé

(

)

( )

txx

dxdt

dxdtf

txx

==x

àëãîðèòì (6.103) ïðèìåò âèä

( )

(

)

( )

1234

16,

kkkk

llll

»+

+++

»+

+++

(6.104)

ãäå

(

)

(

)

( )

1112

0102001020

0101201

0102202

;;

,,,,

;

2,2,2

;

2,2,2

;

2,2,2

;

2,2,2

khflhf

txxtxx

khf

thxkxl

lhf

thxkxl

khf

thxkxl

lhf

thxkxl

+++

183

(

)

( )

0103203

;

khf

thxkxl

lhf

thxkxl

+++

×àñòíûì ñëó÷àåì ìåòîäà Ðóíãå%Êóòòà ÿâëÿåòñÿ ïðÿìîé àëãî-

ðèòì Ýéëåðà (ïðè k

= k

= 0). Îäíàêî îí èìååò ìàëóþ òî÷-

íîñòü è íå íàøåë øèðîêîãî ïðèìåíåíèÿ.

Ðàçíîñòíûå ìåòîäû. Ñóùåñòâåííûì íåäîñòàòêîì ìåòîäà Ðóí-

ãå%Êóòòà ÿâëÿåòñÿ òî, ÷òî äëÿ ïîëó÷åíèÿ êàæäîãî çíà÷åíèÿ ðåøå-

íèÿ õ íåîáõîäèìî âû÷èñëÿòü ïðàâóþ ÷àñòü óðàâíåíèÿ (6.94) â íå-

ñêîëüêèõ òî÷êàõ (äëÿ àëãîðèòìà (6.103) % â ÷åòûðåõ òî÷êàõ). Ýòî

ïðèâîäèò ê áîëüøîìó îáúåìó âû÷èñëåíèé, îñîáåííî äëÿ ñëîæíîé

ïðàâîé ÷àñòè. Ïðèìåíåíèå ðàçíîñòíûõ ìåòîäîâ ïîçâîëÿåò ñóùåñò-

âåííî ñîêðàòèòü îáúåì âû÷èñëåíèé è çàòðàòû ìàøèííîãî âðåìåíè,

òàê êàê íà êàæäîì øàãå ïðàâàÿ ÷àñòü âû÷èñëÿåòñÿ òîëüêî îäèí ðàç.

Â îñíîâå ðàçíîñòíûõ ìåòîäîâ ëåæèò èñïîëüçîâàíèå ðàçëè÷íûõ

èíòåðïîëÿöèîííûõ àëãåáðàè÷åñêèõ ìíîãî÷ëåíîâ (ìíîãî÷ëåíû Íüþ-

òîíà, Ñòèðëèíãà, Ýðìèòà è äð.). Ïðè ýòîì ðåøåíèå x íà (n + 1)

øàãå îïðåäåëÿåòñÿ àëãîðèòìîì

kjki

xxhf

=+b

(6.105)

ãäå h % øàã; b

% ïîñòîÿííûå êîýôôèöèåíòû; f

% çíà÷åíèå àë-

ãåáðàè÷åñêîãî ìíîãî÷ëåíà â òî÷êå k. Êàê ñëåäóåò èç (6.105) äëÿ îï-

ðåäåëåíèÿ ðåøåíèÿ õ

k +

; íåîáõîäèìî çíàòü çíà÷åíèÿ õ

, õ

, ...,

% îíè íàõîäÿòñÿ îáû÷íî ëèáî àíàëèòè÷åñêè, ëèáî ìåòîäîì Ðóí-

ãå%Êóòòà.

Âîïðîñû è çàäàíèÿ äëÿ ñàìîïðîâåðêè

1. Êàêîâû ïðè÷èíû âîçíèêíîâåíèÿ ïåðåõîäíûõ ïðîöåññîâ?

2. Ñôîðìóëèðîâàòü çàêîíû êîììóòàöèè.

3. Äàòü ïîíÿòèÿ ïåðåõîäíîãî, óñòàíîâèâøåãîñÿ è ñâîáîäíîãî ðåæè-

ìîâ â ýëåêòðè÷åñêèõ öåïÿõ.

4. ×òî òàêîå íóëåâûå è íåíóëåâûå íà÷àëüíûå óñëîâèÿ?

5. Êàêîé âèä èìååò ñâîáîäíàÿ ñîñòàâëÿþùàÿ ïåðåõîäíûõ êîëåáà-

íèé â öåïÿõ ïåðâîãî ïîðÿäêà?

6. ×òî ïðåäñòàâëÿåò ñîáîé ïðèíóæäåííàÿ ñîñòàâëÿþùàÿ?

7. Êàê ðàññ÷èòûâàþòñÿ ïîñòîÿííûå èíòåãðèðîâàíèÿ â öåïÿõ ïåðâî-

ãî ïîðÿäêà?

8. ×òî òàêîå ïîñòîÿííàÿ âðåìåíè öåïè?

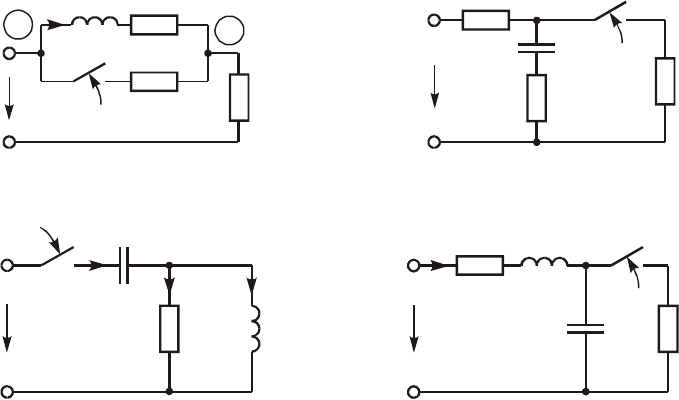
9. Äëÿ ñõåìû, èçîáðàæåííîé íà ðèñ. 6.22, îïðåäåëèòü òîê i(t) è

íàïðÿæåíèå íà êàòóøêå èíäóêòèâíîñòè u

(t), åñëè U = 90 Â;

L = 0,25 Ãí; R

= 20 Îì; R

= R

= 5 Îì.

Îòâåò: i(t) = 3,6 $ 1,6å

100t

, À; u

(t) = 40å

j100t

, Â.

184

Ðèñ. 6.22 Ðèñ. 6.23

Ðèñ. 6.24 Ðèñ. 6.25

10. Äëÿ ñõåìû, èçîáðàæåííîé íà ðèñ. 6.23, íàéòè u

(t), åñëè U =

= 60 Â; R

= R

= 5 êÎì; Ñ = 2,5 ìêÔ.

Îòâåò: u

(t) = 60 $ 30å

40t

, Â.

11. Êàê çàâèñèò õàðàêòåð ñâîáîäíûõ êîëåáàíèé â RLC-êîíòóðå îò

ðàñïîëîæåíèÿ íà êîìïëåêñíîé ïëîñêîñòè êîðíåé õàðàêòåðèñòè-

÷åñêîãî óðàâíåíèÿ?

12. Êàê îïðåäåëÿþòñÿ ÷àñòîòà è ïåðèîä ñâîáîäíûõ êîëåáàíèé?

13. ×òî òàêîå ëîãàðèôìè÷åñêèé äåêðåìåíò çàòóõàíèÿ?

14. Êàêîâà ïîñëåäîâàòåëüíîñòü àíàëèçà ïåðåõîäíûõ ïðîöåññîâ â

ðàçâåòâëåííûõ öåïÿõ âòîðîãî ïîðÿäêà?

15. Äëÿ ñõåìû, ïðèâåäåííîé íà ðèñ. 6.24, íàéòè i

(t) è u

(t), åñëè

U = 100 Â; L = 50 ìÃí; Ñ = 5 ìêÔ; R = 25 Îì.

Îòâåò: i

(t) = 0,29å

$540t

$ 0,29å

$7460t

, À;

(t) = 100 + 8å

540t

$ 108å

$7460t

, Â.

16. Äëÿ ñõåìû, ïðèâåäåííîé íà ðèñ. 6.25, íàéòè i (t) è u

(t), åñëè

U = 60 Â; R

= 250 Îì; R

= 50 Îì; L = 50 ìÃí; C = 0,5 ìêÔ.

Îòâåò: i(t) = 0,22å

$2500t

sin(5800t + 67°), À;

(t) = 60 + 69å

$2500t

sin(5800t $ 46,5°), Â.

17. Â ÷åì çàêëþ÷àåòñÿ ñóòü ìåòîäà ïåðåìåííûõ ñîñòîÿíèÿ? ×òî

ïîíèìàþò ïîä ïåðåìåííûìè ñîñòîÿíèÿ?

18. ×òî òàêîå óðàâíåíèÿ ñîñòîÿíèÿ öåïè? Êàêîâà åãî ìàòðè÷íàÿ

ôîðìà çàïèñè?

19. Â ÷åì ñóùíîñòü ìåòîäà ìàòðè÷íûõ ýêñïîíåíò?

20. Ñóòü ìåòîäà Ðóíãå-Êóòòà.

21. ×òî ëåæèò â îñíîâå ìåòîäîâ ðåøåíèÿ óðàâíåíèÿ ñîñòîÿíèÿ öåïè?

185

ÃËÀÂÀ 7. ÎÏÅÐÀÒÎÐÍÛÉ ÌÅÒÎÄ ÀÍÀËÈÇÀ

ÏÅÐÅÕÎÄÍÛÕ ÏÐÎÖÅÑÑÎÂ Â ËÈÍÅÉÍÛÕ ÖÅÏßÕ

7.1. Ïðåîáðàçîâàíèå Ëàïëàñà è åãî ñâîéñòâà

Îïåðàòîðíûé ìåòîä áåðåò íà÷àëî ñî âðåìåíè àíàëèçà áåñêî-

íå÷íî ìàëûõ âåëè÷èí, êîãäà áûëè îáíàðóæåíû îïðåäåëåííûå àíà-

ëîãèè ìåæäó äèôôåðåíöèàëüíî-èíòåãðàëüíûìè è àëãåáðàè÷åñêèìè

óðàâíåíèÿìè. Â XIX â. áûë îïóáëèêîâàí ðÿä ðàáîò ïî îïåðà-

öèîííîìó èñ÷èñëåíèþ Ì.Å. Âàùåíêî-Çàõàð÷åíêî, Î. Õýâèñàéäà,

Ä. Êàðñîíà è äð. Îäíàêî ñòðîãîå îáîñíîâàíèå îïåðàòîðíûé ìåòîä

ïîëó÷èë òîëüêî â XX â. íà áàçå îáùåé òåîðèè ôóíêöèîíàëüíûõ

ïðåîáðàçîâàíèé.

Â îñíîâå îïåðàòîðíîãî ìåòîäà ðàñ÷åòà ïåðåõîäíûõ ïðîöåññîâ

ëåæèò ïðåîáðàçîâàíèå Ëàïëàñà, êîòîðîå ïîçâîëÿåò ïåðåíåñòè ðå-

øåíèå èç îáëàñòè ôóíêöèé äåéñòâèòåëüíîãî ïåðåìåííîãî t â îá-

ëàñòü êîìïëåêñíîãî ïåðåìåííîãî ð:

=a+w

(7.1)

Ïðè ýòîì îïåðàöèè äèôôåðåíöèðîâàíèÿ è èíòåãðèðîâàíèÿ ôóíê-

öèé âðåìåíè çàìåíÿþòñÿ ñîîòâåòñòâóþùèìè îïåðàöèÿìè óìíîæå-

íèÿ è äåëåíèÿ ôóíêöèé êîìïëåêñíîãî ïåðåìåííîãî íà îïåðàòîð ð,

÷òî ñóùåñòâåííî óïðîùàåò ðàñ÷åò, òàê êàê ñâîäèò ñèñòåìó äèôôå-

ðåíöèàëüíûõ óðàâíåíèé ê ñèñòåìå àëãåáðàè÷åñêèõ. Â îïåðàòîðíîì

ìåòîäå îòïàäàåò íåîáõîäèìîñòü îïðåäåëåíèÿ ïîñòîÿííûõ èíòåãðè-

ðîâàíèÿ. Ýòèìè îáñòîÿòåëüñòâàìè îáúÿñíÿåòñÿ øèðîêîå ïðèìåíå-

íèå ýòîãî ìåòîäà íà ïðàêòèêå.

Ðàçëè÷àþò ïðÿìîå è îáðàòíîå ïðåîáðàçîâàíèå Ëàïëàñà. Ïðÿìîå

ïðåîáðàçîâàíèå Ëàïëàñà îïðåäåëÿåòñÿ óðàâíåíèåì.

( )

()

Ffedt

(7.2)

ãäå f(t) % ôóíêöèÿ äåéñòâèòåëüíîãî ïåðåìåííîãî t, îïðåäåëåííàÿ

ïðè t



0 (ïðè t < 0; f(t) = 0) è óäîâëåòâîðÿþùàÿ óñëîâèÿì îãðà-

íè÷åííîãî ðîñòà:

()

(7.3)

ãäå ìíîæèòåëü Ì è ïîêàçàòåëü ðîñòà ñ

% ïîëîæèòåëüíûå äåéñò-

âèòåëüíûå ÷èñëà. Íà ðèñ. 7.1 èçîáðàæåíà îáëàñòü îïðåäåëåíèÿ

ôóíêöèè êîìïëåêñíîãî ïåðåìåííîãî F(p).

Îáðàòíîå ïðåîáðàçîâàíèå Ëàïëàñà îïðåäåëÿþò èç ðåøåíèÿ

(7.2):

( )

+¥

-¥

fFedp

(7.4)

186

Ðèñ. 7.1

Ôóíêöèÿ F(p), îïðåäåëÿåìàÿ óðàâíåíèåì

(7.2), íîñèò íàçâàíèå èçîáðàæåíèÿ ïî Ëàïëà-

ñó, à ôóíêöèÿ f (t) â (7.4) % îðèãèíàëà. Ñëå-

äîâàòåëüíî, îðèãèíàë è èçîáðàæåíèå ïðåä-

ñòàâëÿþò ñîáîé ïàðó ôóíêöèé äåéñòâèòåëü-

íîãî f(t) è êîìïëåêñíîãî F(p) ïåðåìåííîãî,

ñâÿçàííûõ ïðåîáðàçîâàíèåì Ëàïëàñà. Äëÿ

ñîêðàùåííîé çàïèñè ïðåîáðàçîâàíèé (7.2),

(7.4) èñïîëüçóþò ñëåäóþùóþ ñèìâîëèêó:

()

( )

()

( ) ( )

()

( )

€

;;;,

fFfFFLfLF

pppp

ttt



ãäå L % îïåðàòîð Ëàïëàñà. Â äàëüíåéøåì äëÿ îïðåäåëåííîñòè áó-

äåì èñïîëüçîâàòü çíàê ñîîòâåòñòâèÿ



Ðàññìîòðèì îñíîâíûå ñâîéñòâà ïðåîáðàçîâàíèé Ëàïëàñà.

Ñâîéñòâî ëèíåéíîñòè ÿâëÿåòñÿ ñëåäñòâèåì ëèíåéíîñòè ïðåîá-

ðàçîâàíèÿ Ëàïëàñà, åãî ìîæíî çàïèñàòü â ôîðìå

()

( )

åå

kkkk

afaF

 (7.5)

ãäå a

% ïîñòîÿííûå êîýôôèöèåíòû ðàçëîæåíèÿ. Ñâîéñòâî (7.5)

ëåãêî äîêàçàòü, åñëè ïðèìåíèòü ê ëåâîé ÷àñòè ñîîòíîøåíèÿ (7.5)

ïðÿìîå ïðåîáðàçîâàíèå Ëàïëàñà (7.2).

Äèôôåðåíöèðîâàíèå îðèãèíàëà. Ïðè íåíóëåâûõ íà÷àëüíûõ óñ-

ëîâèÿõ: f (0

) ¹ 0 äèôôåðåíöèðîâàíèå îðèãèíàëà ñîîòâåòñòâóåò ñëå-

äóþùåìó óñëîâèþ

(

)

(

)

(

)

fpFf

 (7.6)

Äëÿ äîêàçàòåëüñòâà (7.6) ïîäñòàâèì f¢(t) â ïðåîáðàçîâàíèå (7.2)

â âèäå

() ()

¥¥

òò

ptpt

fedtedf

Îòñþäà ïîñëå èíòåãðèðîâàíèÿ ïî ÷àñòÿì ïîëó÷àåì:

()

( )

¥¥

=+=-

òò

ptpt

edfpefdtpFf

Â ñëó÷àå íóëåâûõ íà÷àëüíûõ óñëîâèé

()

( )

()

( )

()

( )

¢¢¢

;;.

fpFfpFfpF

ppp

ttt

 (7.7)

Èíòåãðèðîâàíèå îðèãèíàëà

()

(

)

{

()

(

)

òòò

000

ðàç

ttt

fdtfdt

 (7.8)

187

Äîêàçàòåëüñòâî îñóùåñòâëÿåòñÿ ïóòåì èñïîëüçîâàíèÿ ñâîéñòâà

äèôôåðåíöèðîâàíèÿ îðèãèíàëà (7.6), (7.7).

Èçìåíåíèå ìàñøòàáà íåçàâèñèìîãî ïåðåìåííîãî (òåîðåìà ïî-

äîáèÿ)

( )

æö

ç÷

èø

 (7.9)

ãäå à % ïîñòîÿííûé âåùåñòâåííûé êîýôôèöèåíò. Ñâîéñòâî (7.9)

ëåãêî äîêàçûâàåòñÿ ïóòåì çàìåíû íåçàâèñèìîé ïåðåìåííîé t = at â

ïðÿìîì ïðåîáðàçîâàíèè Ëàïëàñà (7.2).

Ñìåùåíèå â îáëàñòè äåéñòâèòåëüíîãî ïåðåìåííîãî (òåîðåìà

çàïàçäûâàíèÿ):

( )

feF

 (7.10)

Äëÿ äîêàçàòåëüñòâà (7.10) ââåäåì ñëåäóþùèå îáîçíà÷åíèÿ:

( )

fedt

Îñóùåñòâèì çàìåíó ïåðåìåííîé t = t ± t

( )

fedefed

¥¥

-t

Y=tt=tt=

òò

÷òî è òðåáîâàëîñü äîêàçàòü.

Èç ñîîòíîøåíèÿ (7.10) ñëåäóåò, ÷òî ñäâèã îðèãèíàëà ïî îñè

âðåìåíè íà t

ñîîòâåòñòâóåò óìíîæåíèþ èçîáðàæåíèÿ íà

Ñìåùåíèÿ â îáëàñòè êîìïëåêñíîãî ïåðåìåííîãî (òåîðåìà ñìå-

ùåíèÿ):

( )

()

±l

Fef

 (7.11)

Òåîðåìà (7.11) ñëåäóåò íåïîñðåäñòâåííî èç ïðÿìîãî ïðåîáðàçî-

âàíèÿ Ëàïëàñà, åñëè â (7.2) âìåñòî f (t) ïîäñòàâèòü

()

±lt

. Ïðè-

÷åì l ìîæåò áûòü êàê äåéñòâèòåëüíîé, òàê è êîìïëåêñíîé âåëè-

÷èíîé.

Äèôôåðåíöèðîâàíèå è èíòåãðèðîâàíèå îðèãèíàëà ïî ïàðàìåò-

ðó (ñâîéñòâî êîììóòàòèâíîñòè):

( )

¶¶

;

 (7.12)

( )

òò

fdxFdx



(7.13)

Äëÿ äîêàçàòåëüñòâà ñâîéñòâ (7.12), (7.13) äîñòàòî÷íî ïðîäèô-

ôåðåíöèðîâàòü èëè ïðîèíòåãðèðîâàòü ïðÿìîå ïðåîáðàçîâàíèå Ëàï-

ëàñà (7.2) ïî ïàðàìåòðó õ.

188

()

)

Ðèñ. 7.2

Ïðîèçâåäåíèå èçîáðàæåíèé:

( ) ( )

( ) ( ) ( ) ( )

òò

121212

FFffdxffdx

txxxtx

 (7.14)

Èíòåãðàëû â (7.14) íîñÿò íàçâàíèå ñâåðòêè ôóíêöèé f

(t) è f

(t).

Äèôôåðåíöèðîâàíèå èçîáðàæåíèÿ:

( )

( ) ()

 (7.15)

Ñâîéñòâî (7.15) ëåãêî äîêàçûâàåòñÿ ïóòåì äèôôåðåíöèðîâàíèÿ

ïðÿìîãî ïðåîáðàçîâàíèÿ Ëàïëàñà (7.2).

Èíòåãðèðîâàíèå èçîáðàæåíèÿ:

( )

()

Fdp

 (7.16)

Äàííîå ñâîéñòâî äîêàçûâàåòñÿ àíàëîãè÷íî (7.15).

Â çàêëþ÷åíèå ïðèâåäåì ïðåäåëüíûå ñîîòíîøåíèÿ äëÿ îðèãè-

íàëà è èçîáðàæåíèÿ:

(

)

(

)

®®¥

limlim;

fpF

(7.17)

(

)

(

)

®¥®

limlim.

fpF

(7.18)

Äåéñòâèòåëüíî, ñîãëàñíî ñâîéñòâà äèôôåðåíöèðîâàíèÿ îðèãè-

íàëà ìîæíî çàïèñàòü:

()

( )

()

fedtpFf

Ó÷èòûâàÿ, ÷òî

®¥

lim0

e , ïîëó÷àåì:

(

)

(

)

[

]

(

)

(

)

®¥®¥®

-=-=

limlimlim0.

ppt

pFfpFf

Îòñþäà íåïîñðåäñòâåííî ñëåäóåò ñîîòíîøåíèå (7.17). Àíàëîãè÷íî

äîêàçûâàåòñÿ ðàâåíñòâî (7.18).

Â êà÷åñòâå ïðèìåðà íàéäåì èçîáðàæåíèå ïî Ëàïëàñó òèïî-

âûõ ñèãíàëîâ. Äëÿ òåîðåòè÷åñêèõ è ýêñïåðèìåíòàëüíûõ èññëå-

äîâàíèé õàðàêòåðèñòèê ýëåêòðè÷åñêèõ öåïåé è ïåðåäà÷è ñîîá-

189

()

t-t

-1

Ðèñ. 7.3

Ðèñ. 7.4

ùåíèé ïî êàíàëàì ñâÿçè èñïîëüçóþòñÿ ðàçëè÷íûå òèïû ñèãíà-

ëîâ: ãàðìîíè÷åñêèå êîëåáàíèÿ, óðîâíè ïîñòîÿííûõ íàïðÿæå-

íèé, ïîñëåäîâàòåëüíîñòü ïðÿìîóãîëüíûõ èìïóëüñîâ è òàê äàëåå.

Îñîáî âàæíóþ ðîëü â òåîðåòè÷åñêèõ èññëåäîâàíèÿõ ýëåêòðè÷å-

ñêèõ öåïåé èãðàþò èñïûòàòåëüíûå ñèãíàëû â ôîðìå åäèíè÷íîé

ôóíêöèè 1(t) è åäèíè÷íîé èìïóëüñíîé ôóíêöèè d(t) (ôóíêöèÿ

Äèðàêà).

Åäèíè÷íàÿ ôóíêöèÿ. Åäèíè÷íàÿ ôóíêöèÿ çàäàåòñÿ óðàâíåíèåì

(ðèñ. 7.2, à)

( )

{

ïðè 0,

ïðè 0.



(7.19)

Èçîáðàæåíèå ôóíêöèè (7.19) áóäåò ðàâíî:

( )

ò. å., 1.

Fedt

 (7.20)

Åäèíè÷íàÿ èìïóëüñíàÿ ôóíêöèÿ (ôóíêöèÿ Äèðàêà). Ýòà ôóíê-

öèÿ íàçûâàåòñÿ åùå d-ôóíêöèåé; îíà çàäàåòñÿ óðàâíåíèåì

( )

¥=

ïðè 0,

ïðè 0.

(7.21)

Ôóíêöèÿ Äèðàêà ÿâëÿåòñÿ ôèçè÷åñêè íåðåàëèçóåìîé ìàòåìà-

òè÷åñêîé àáñòðàêöèåé, îäíàêî îáëàäàåò ðÿäîì èíòåðåñíûõ ñâîéñòâ

è èãðàåò î÷åíü âàæíóþ ðîëü â òåîðåòè÷åñêèõ èññëåäîâàíèÿõ. Ôîð-

ìàëüíî îíà ìîæåò áûòü ïîëó÷åíà, íàïðèìåð, ïðåäåëüíûì ïåðåõî-

äîì (ïðè t ® 0) åäèíè÷íîãî èìïóëüñà (ñì. ðèñ. 7.2, á), ïëîùàäü

êîòîðîãî ðàâíà åäèíèöå:

()

-¥

=d=

Sdt

(7.22)

Îäíèì èç èíòåðåñíûõ ñâîéñòâ ôóíêöèè d(t) ÿâëÿåòñÿ åå ôèëüò-

ðóþùåå ñâîéñòâî, îïðåäåëÿåìîå ðàâåíñòâîì (ðèñ. 7.3):

()

( ) ( )

-¥

fdtf

ttt

(7.23)

190

Òàáëèöà 7.1

ï/ï

Îðèãèíàë f (t) Èçîáðàæåíèå F (p)

A = const

(

)

w+j

-w

-a

( )

sin

cos

(

)

sin

w+j

sincos

j+wj

(

)

cos

w+j

cossin

j-wj

sin

-a

( )

cos

-a

( )

Ate

-a

( )

Íàéäåì èçîáðàæåíèå åäèíè÷íîé èìïóëüñíîé ôóíêöèè â ôîðìå

èçîáðàæåíèÿ ðàçíîñòè äâóõ åäèíè÷íûõ ôóíêöèé âåëè÷èíû 1(t),

ñäâèíóòûõ äðóã îòíîñèòåëüíî äðóãà íà t (ðèñ. 7.4). Äëÿ ýòèõ

ôóíêöèé ñ ó÷åòîì òåîðåìû çàïàçäûâàíèÿ èìååì:

(

)

( )

-t

Äëÿ ðåçóëüòèðóþùåãî èçîáðàæåíèÿ ñ ó÷åòîì ñâîéñòâà ëèíåéíîñòè

ïîëó÷èì