Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.

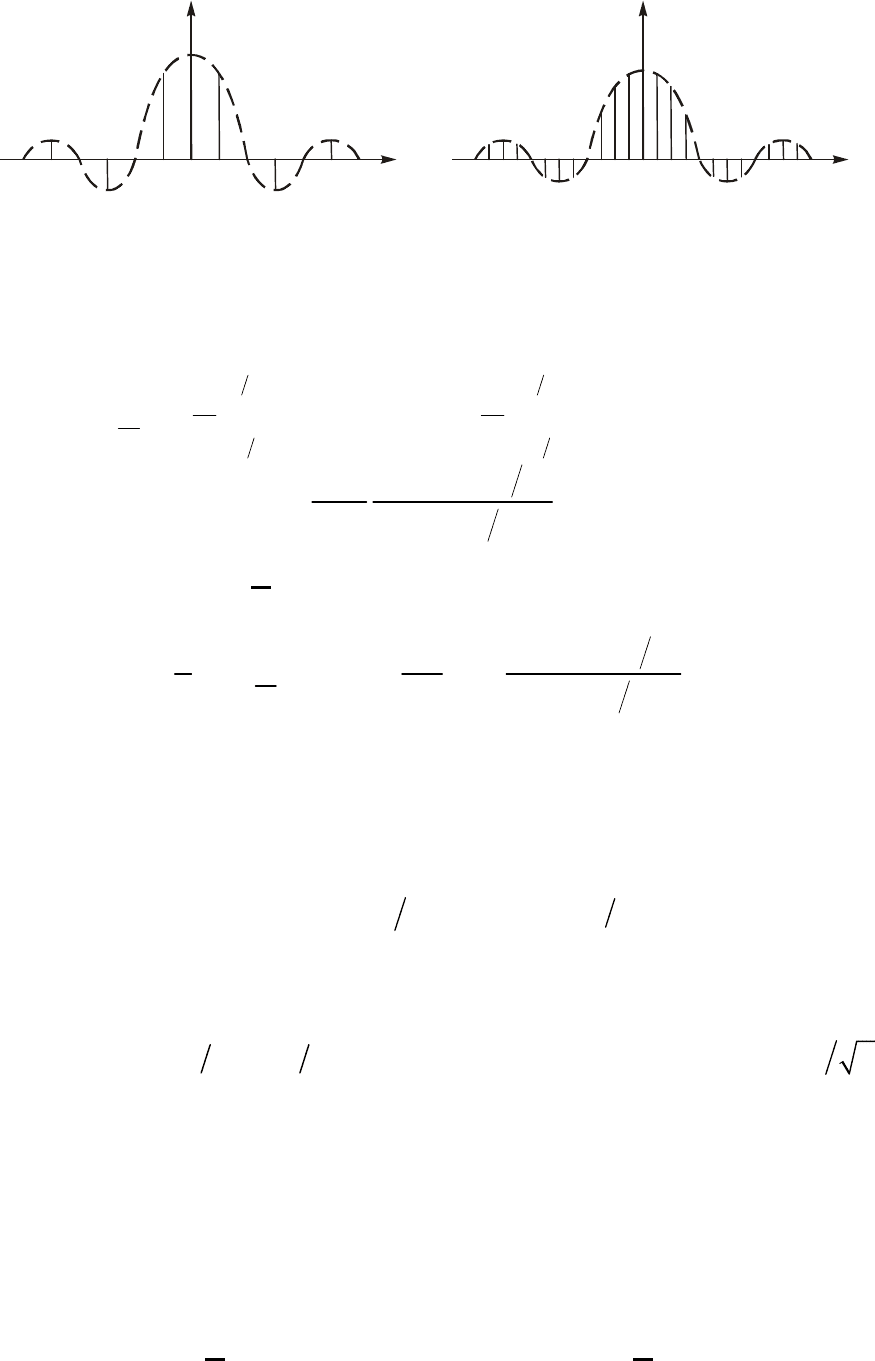
151
Êîìïëåêñíàÿ àìïëèòóäà k-é ãàðìîíèêè ðàâíà ñîãëàñíî (5.8) ïîñëå
âîçâðàùåíèÿ ê èñõîäíîé ïåðåìåííîé t.
()
( )
è
11
è
22
è
22
1è
è
1è
22
2
sin
2
.
2
Tt
jktjkt
k
Tt
AfedtAedt
t
TT
kt
A
qkt
-ww
--
===
w
=
w
òò
(5.27)
Ïîäñòàâèâ çíà÷åíèå A
k
â óðàâíåíèå (5.6), ïîëó÷èì ðàçëîæåíèå â
ðÿä Ôóðüå:
()
(
)
11
1 è
è
1 è
2
sin
1
.
22
jktjkt
k
kk
kt
A
fAee
t
qkt
¥¥
ww
=-¥=-¥
w
==
w
åå
(5.28)
Íà ðèñ. 5.4 èçîáðàæåí ñïåêòð êîìïëåêñíûõ àìïëèòóä äëÿ q = 2
è q = 4. Êàê âèäíî èç ðèñóíêà, ñïåêòð ïîñëåäîâàòåëüíîñòè ïðÿìî-
óãîëüíûõ èìïóëüñîâ ïðåäñòàâëÿåò ñîáîé äèñêðåòíûé ñïåêòð ñ îãè-
áàþùåé (øòðèõîâàÿ ëèíèÿ íà ðèñ. 5.4), êîòîðàÿ îïèñûâàåòñÿ
ôóíêöèåé
(
)
(
)
sin,
ãäå ,
fxxxxkq
==p
(5.29)
íîñÿùåé íàçâàíèå ôóíêöèè îòñ÷åòîâ (ñì. ãë. 19). ×èñëî ñïåêòðàëü-
íûõ ëèíèé ìåæäó íà÷àëîì îòñ÷åòà ïî îñè ÷àñòîò è ïåðâûì íóëåì
îãèáàþùåé ðàâíî q%1. Ïîñòîÿííàÿ ñîñòàâëÿþùàÿ ñèãíàëà (ñðåä-
íåå çíà÷åíèå)
0 è
2
aAq
=
, à äåéñòâóþùåå çíà÷åíèå A =
è
Aq
,
ò. å. ÷åì áîëüøå ñêâàæíîñòü, òåì ìåíüøå óðîâåíü ïîñòîÿííîé ñî-
ñòàâëÿþùåé è äåéñòâóþùåå çíà÷åíèå ñèãíàëà. Ñ óâåëè÷åíèåì
ñêâàæíîñòè q ÷èñëî äèñêðåòíûõ ñîñòàâëÿþùèõ óâåëè÷èâàåòñÿ %
ñïåêòð ñòàíîâèòñÿ ãóùå (ñì. ðèñ. 5.4, á), è àìïëèòóäà ãàðìîíèê
óáûâàåò ìåäëåííåå. Ñëåäóåò ïîä÷åðêíóòü, ÷òî â ñîîòâåòñòâèè ñ
(5.27) ñïåêòð ðàññìàòðèâàåìîé ïîñëåäîâàòåëüíîñòè ïðÿìîóãîëüíûõ
èìïóëüñîâ âåùåñòâåííûé.
Èç ñïåêòðà êîìïëåêñíûõ àìïëèòóä (5.27) ìîæíî âûäåëèòü àì-
ïëèòóäíûé A
k
= |A
k
| è ôàçîâûé ñïåêòð j
k
= argA
k
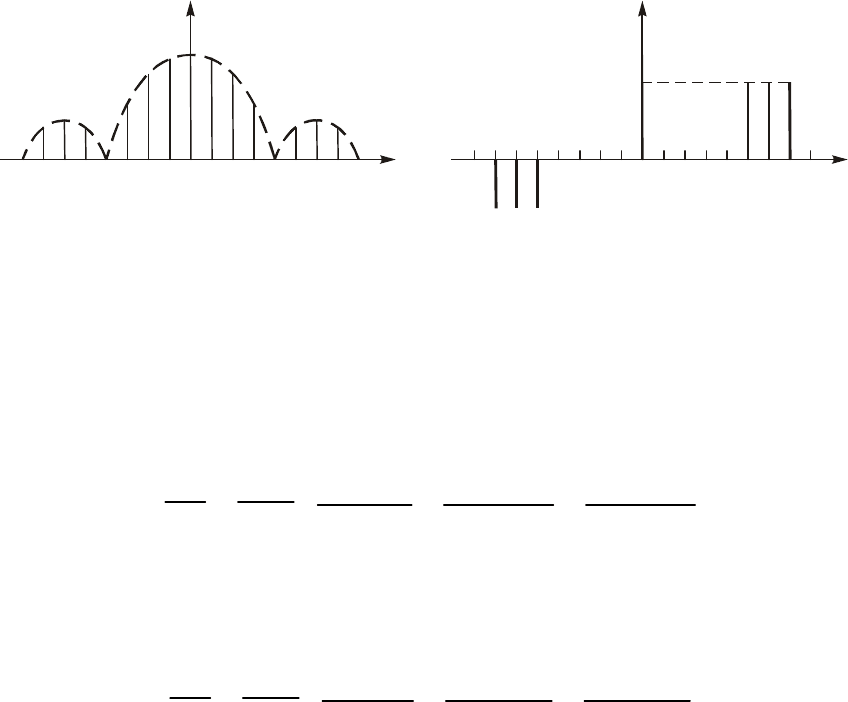
, èçîáðàæåííûé
íà ðèñ. 5.5 äëÿ ñëó÷àÿ q = 4. Èç ðèñóíêîâ âèäíî, ÷òî àìïëèòóäíûé
ñïåêòð ÿâëÿåòñÿ ÷åòíîé, à ôàçîâûé % íå÷åòíîé ôóíêöèåé ÷àñòîòû.
Ïðè÷åì, ôàçû îòäåëüíûõ ãàðìîíèê ïðèíèìàþò ëèáî íóëåâîå çíà-
0
A
k
/2
À
è
/2
1-1-2-4-5-6 2 45 6
3-3
k
0
A
k
/2
-4-8
-12
4 8 12
k
à
)
á
)
q
= 2
q
= 4
Ðèñ. 5.4
152
÷åíèå ìåæäó óçëàìè, ãäå ñèíóñ ïîëîæèòåëüíûé, ëèáî ±p, ãäå ñèíóñ
îòðèöàòåëüíûé (ðèñ. 5.5, á)
Íà îñíîâàíèè ôîðìóëû (5.28) ïîëó÷èì òðèãîíîìåòðè÷åñêóþ
ôîðìó ðàçëîæåíèÿ â ðÿä Ôóðüå ïî ÷åòíûì ãàðìîíèêàì (ñðàâíè ñ
(5.15)):
()
èè111
4coscos3cos5
.
135
AAttt
f
t
q
www
æö
=+
-+-
ç÷
p
èø
K
(5.30)
Ïðè ñäâèãå èìïóëüñíîé ïîñëåäîâàòåëüíîñòè ïî îñè âðåìåíè
(ðèñ. 5.2, á) â ñîîòâåòñòâèè ñ (5.13) åå àìïëèòóäíûé ñïåêòð îñòà-
íåòñÿ ïðåæíèì, à ôàçîâûé ñïåêòð èçìåíèòñÿ:
( )
èè111
4sinsin3sin5
.
135
AAttt
f
t
q
www
æö
=+
+++
ç÷
p
èø
K
(5.31)
 ñëó÷àå, êîãäà ïåðèîäè÷åñêàÿ ïîñëåäîâàòåëüíîñòü èìååò ðàçíî-
ïîëÿðíóþ ôîðìó (ñì. ðèñ. 5.1), â ñïåêòðå áóäåò îòñóòñòâîâàòü ïî-
ñòîÿííàÿ ñîñòàâëÿþùàÿ (ñðàâíèòå (5.30) è (5.31) ñ (5.14) è (5.15)).
Àíàëîãè÷íûì îáðàçîì ìîæíî èññëåäîâàòü ñïåêòðàëüíûé ñîñòàâ
ïåðèîäè÷åñêèõ íåãàðìîíè÷åñêèõ ñèãíàëîâ äðóãîé ôîðìû. Â
òàáë. 5.1 ïðèâåäåíî ðàçëîæåíèå â ðÿä Ôóðüå íåêîòîðûõ íàèáîëåå
ðàñïðîñòðàíåííûõ ñèãíàëîâ.
5.4. Ðàñ÷åò öåïåé ïðè ïåðèîäè÷åñêèõ íåãàðìîíè÷åñêèõ
âîçäåéñòâèÿõ
 îñíîâå ðàñ÷åòà ëèíåéíûõ ýëåêòðè÷åñêèõ öåïåé, íàõîäÿùèõñÿ
ïîä âîçäåéñòâèåì ïåðèîäè÷åñêèõ íåãàðìîíè÷åñêèõ ñèãíàëîâ, ëåæèò
ïðèíöèï íàëîæåíèÿ (ñì. § 1.6). Åãî ñóòü ïðèìåíèòåëüíî ê íåãàð-
ìîíè÷åñêèì âîçäåéñòâèÿì çàêëþ÷àåòñÿ â ðàçëîæåíèè íåãàð-
ìîíè÷åñêîãî ïåðèîäè÷åñêîãî ñèãíàëà â îäíó èç ôîðì ðÿäà Ôóðüå
(ñì. § 5.1) è îïðåäåëåíèè ðåàêöèè öåïè îò êàæäîé ãàðìîíèêè â îò-
äåëüíîñòè. Ðåçóëüòèðóþùàÿ ðåàêöèÿ íàõîäèòñÿ ïóòåì ñóïåðïî-
çèöèè (íàëîæåíèÿ) ïîëó÷åííûõ ÷àñòè÷íûõ ðåàêöèé. Òàêèì îáðà-
çîì, ðàñ÷åò öåïåé ïðè ïåðèîäè÷åñêèõ íåãàðìîíè÷åñêèõ âîçäåéñò-
âèÿõ âêëþ÷àåò â ñåáÿ çàäà÷ó àíàëèçà ñïåêòðàëüíîãî ñîñòàâà ñèã-
íàëà (ðàçëîæåíèå åãî â ðÿä Ôóðüå), ðàñ÷åò öåïè îò êàæäîé ãàð-
0
A
k
/2
À
è
/2
1-1-2-4-8 2 456
k
j
k
k
à
)
á
)
378-3
0
1
-1-2-4-8 2 43 8-3
p
Ðèñ. 5.5
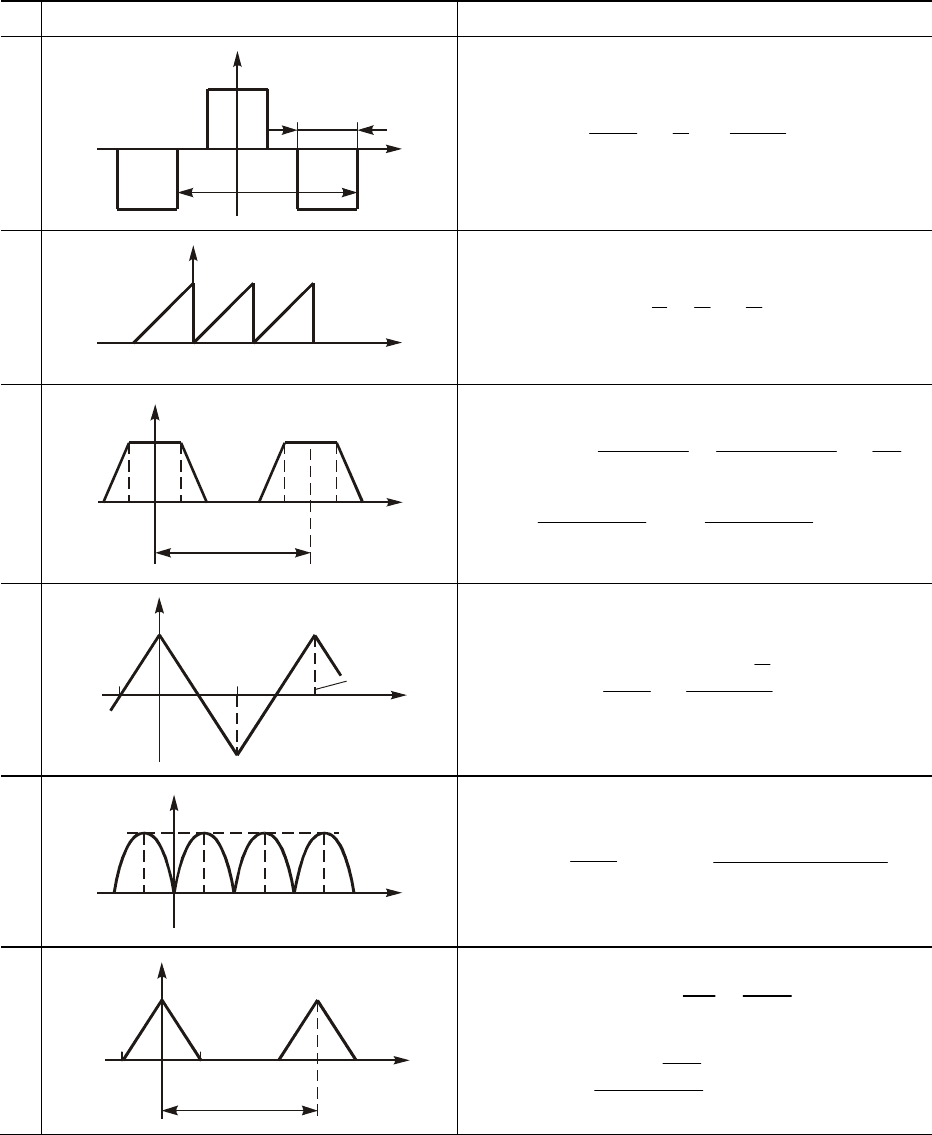
153
ìîíè÷åñêîé ñîñòàâëÿþùåé è çàäà÷ó ñèíòåçà, â ðåçóëüòàòå êîòîðîãî
îïðåäåëÿåòñÿ ðåçóëüòèðóþùèé âûõîäíîé ñèãíàë êàê ôóíêöèÿ âðå-
ìåíè (÷àñòîòû) èëè åãî äåéñòâóþùåå (àìïëèòóäíîå çíà÷åíèå).
Ïðè ðåøåíèè çàäà÷è àíàëèçà îáû÷íî ïîëüçóþòñÿ òðèãîíîìåò-
ðè÷åñêîé (5.3) èëè êîìïëåêñíîé (5.6) ôîðìîé ðÿäà Ôóðüå ñ îãðà-
íè÷åííûì ÷èñëîì ÷ëåíîâ ðàçëîæåíèÿ, ÷òî ïðèâîäèò ê íåêîòîðîé
ïîãðåøíîñòè àïïðîêñèìàöèè èñòèííîãî ñèãíàëà. Êîýôôèöèåíòû
ðàçëîæåíèÿ a
k
è b
k
â (5.3) èëè A
k
è j
k
â (5.6) îïðåäåëÿþòñÿ ñ ïî-
Òàáëèöà 5.1
Òèïû ñèãíàëà Ðàçëîæåíèå â ðÿä Ôóðüå
1
f
t
(
)
t
t
è
T
A
è
( )
1
è
1
1
41
sincos
2
k
kt
A
fkt
t
k
¥
=
w
=w
p
å
2
t
T
A
è
2T
0
( )
è
1
1
111
sin
2
k
fA
kt
t
k
¥
=
éù
=
-w
êú
p
ëû
å
3
f
t
(
)
t
t
2
T
A
è
t
1
t
1
t
2
0
( )
(
)
( )
( ) ( )
12
è
22
1
21
1221
1
21
sinsincos
k
tt
T
fA
t
T
k
tt
tttt
kkkt
TT
¥
=
é
+
+´
=
ê
p
-
ë
pp
+-
ù
´w
ú
û
å
4
f
t
(
)
t
T
A
è
T
/
4
0
T
/
2
-A
è
3/4
T
( )
2
è
1
22
1
sin
8
2
cos
k
k
A
fkt
t
k
¥
=
p
=w
p
å
5
f
t
(
)
t
T
A
è
T/2
-T/2-T
( )
(
)
1
è
2
1
2
cos
2
12
41
k
kt
A
f
t
k
¥
=
w+p
éù
=
+
êú
p
-
ëû
å
6
f
t
(
)
t
A
è
0
T
t
è
/2
-t
è
/2
( )
è
è
2
1
è
2
è
1
2
4
2
sin
2
cos
k
tT
fA
t
T
t
t
k
T
kt
k
¥
=
é
+´
=
ê
p
ë
p
ù
ú
´w
ú
û
å
154
ìîùüþ óðàâíåíèé (5.4), (5.7) è (5.8). Ïðè ýòîì âõîäíîé ñèãíàë
f(a) äîëæåí áûòü çàäàí àíàëèòè÷åñêè.  ñëó÷àå, åñëè ñèãíàë çàäà-
åòñÿ ãðàôè÷åñêè, íàïðèìåð â âèäå îñöèëëîãðàììû, òî äëÿ íàõîæ-
äåíèÿ êîýôôèöèåíòîâ ðàçëîæåíèÿ a
k
è b
k
ìîæíî èñïîëüçîâàòü
ãðàôîàíàëèòè÷åñêèé ìåòîä (ñì. (5.16)).
Ðàñ÷åò öåïè îò îòäåëüíûõ ãàðìîíèê âåäåòñÿ îáû÷íî ñèìâîëè-
÷åñêèì ìåòîäîì (ñì. ãë. 3). Ïðè ýòîì íåîáõîäèìî èìåòü â âèäó,
÷òî íà k-é ãàðìîíèêå èíäóêòèâíîå ñîïðîòèâëåíèå X
L
(k) = kwL, à
åìêîñòíîå ñîïðîòèâëåíèå X
C
(k) = 1/(kwÑ), ò. å. íà k-é ãàðìîíèêå
èíäóêòèâíîå ñîïðîòèâëåíèå â k ðàç áîëüøå, à åìêîñòíîå â k ðàç
ìåíüøå, ÷åì íà ïåðâîé ãàðìîíèêå. Ýòèì â ÷àñòíîñòè îáúÿñíÿåòñÿ
òî îáñòîÿòåëüñòâî, ÷òî âûñîêèå ãàðìîíèêè â åìêîñòè âûðàæåíû
ñèëüíåå, à â èíäóêòèâíîñòè ñëàáåå, ÷åì â ïðèëîæåííîì ê íèì íà-
ïðÿæåíèè. Àêòèâíîå ñîïðîòèâëåíèå R íà íèçêèõ è ñðåäíèõ ÷àñòî-
òàõ ìîæíî ñ÷èòàòü íå çàâèñÿùèì îò ÷àñòîòû.
Ïîñëå îïðåäåëåíèÿ èñêîìûõ òîêîâ è íàïðÿæåíèé îò îòäåëüíûõ
ãàðìîíèê ìåòîäîì íàëîæåíèÿ íàõîäÿò ðåçóëüòèðóþùóþ ðåàêöèþ
öåïè íà íåãàðìîíè÷åñêîå ïåðèîäè÷åñêîå âîçäåéñòâèå. Ïðè ýòîì ëè-
áî îïðåäåëÿþò ìãíîâåííîå çíà÷åíèå ðåçóëüòèðóþùåãî ñèãíàëà íà îñ-
íîâàíèè ðàñ÷åòà àìïëèòóä è ôàç îòäåëüíûõ ãàðìîíèê, ëèáî åãî àì-
ïëèòóäíûå èëè äåéñòâóþùèå çíà÷åíèÿ ñîãëàñíî óðàâíåíèÿì (5.18),
(5.19). Ïðè îïðåäåëåíèè ðåçóëüòèðóþùåé ðåàêöèè íåîáõîäèìî ïîì-
íèòü, ÷òî â ñîîòâåòñòâèè ñ ïðåäñòàâëåíèåì ïåðèîäè÷åñêèõ íåãàðìî-
íè÷åñêèõ êîëåáàíèé íà êîìïëåêñíîé ïëîñêîñòè (ñì. § 3.2) âåêòîðû
ðàçëè÷íûõ ãàðìîíèê âðàùàþòñÿ ñ ðàçëè÷íîé óãëîâîé ÷àñòîòîé.
Ïðèìåð. Ê öåïè, èçîáðàæåííîé íà ðèñ. 5.6, ïðèëîæåíî íàïðÿæåíèå u(t) â
ôîðìå ïðÿìîóãîëüíûõ èìïóëüñîâ ñ ïåðèîäîì ïîâòîðåíèÿ T = 2t
è
è àìïëèòó-
äîé A
è
= 1 (ñì. ðèñ. 5.3, á). Îïðåäåëèòü ìãíîâåííîå è äåéñòâóþùåå çíà÷å-
íèÿ íàïðÿæåíèÿ íà åìêîñòè.
Ðàçëîæåíèå äàííîãî íàïðÿæåíèÿ â ðÿä Ôóðüå îïðåäåëÿåòñÿ ïî ôîðìóëå
(5.31). Îãðàíè÷èìñÿ ïåðâûìè òðåìÿ ÷ëåíàìè ðàçëîæåíèÿ (5.31):
( )
11
4sin4sin3
1
.
23
tt
u
t
ww
=++
pp
Òàêèì îáðàçîì, ïðèëîæåííîå íàïðÿæåíèå ñîäåðæèò ïîñòîÿííóþ ñîñòàâëÿþ-
ùóþ U
0
= 1/2, ïåðâóþ U
1
= 4/p è òðåòüþ U
3
= 4/(3p) ãàðìîíèêè ñ íóëåâû-
ìè íà÷àëüíûìè ôàçàìè. Íàéäåì íàïðÿæåíèå íà åìêîñòè îò ïîñòîÿííîé ñî-
ñòàâëÿþùåé ïðèëîæåííîãî íàïðÿæåíèÿ U
0
:
( ) ( )
0
222
00
12
C
U
UIRR
RR
==
+
.
Êîìïëåêñíîå äåéñòâóþùåå íàïðÿæåíèå îò ïåðâîé ãàðìîíèêè
()
() ()
( )
21
3121
1
1
1
.
C
UII
RjL
jC
==
+w
w
Òîêè I
2(1)
èëè I
3(1)
ìîæíî íàéòè ïî ôîðìóëå ðàçáðîñà (ñì.§ 2.2). Íàïðèìåð,
äëÿ I
3(1)
èìååì:
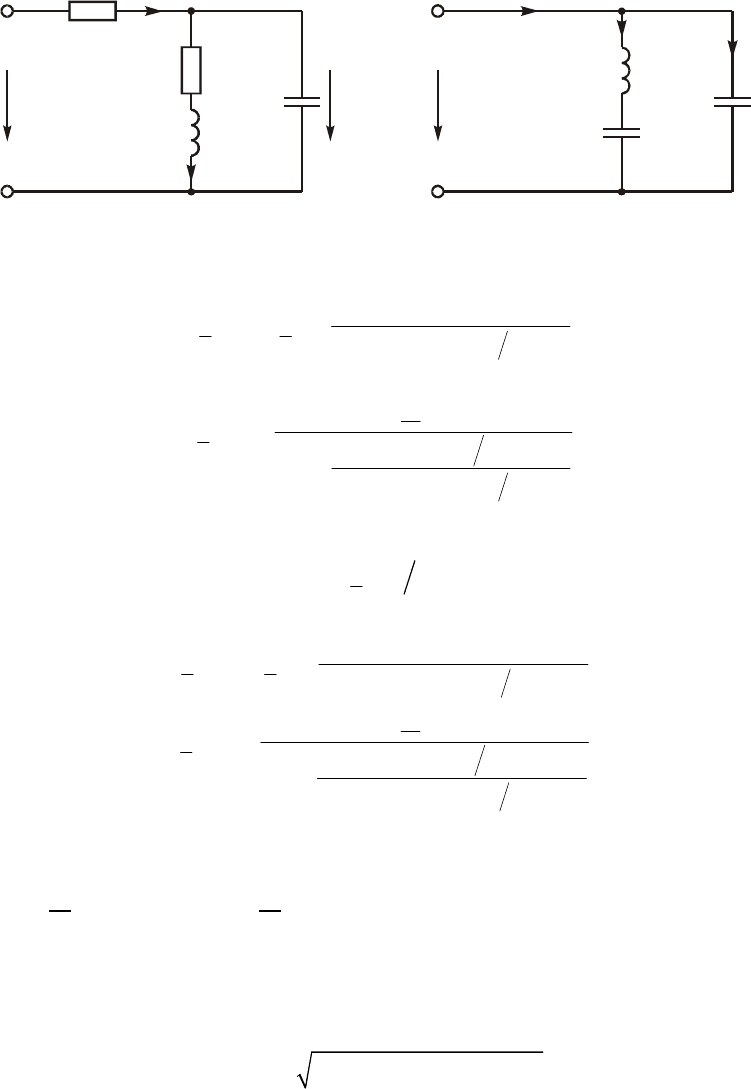
155
() ()
( )
21
3111
11
2
,
1
RjL
II
LC
Rj
+w
=
w-w
+
ãäå
()
()
( )( )
( )
1
11
211
1
11
2
.
1
U
I
RjLjC
R
LC
Rj
=
+ww
+
w-w
+
Àíàëîãè÷íûì îáðàçîì íàõîäèòñÿ íàïðÿæåíèå íà åìêîñòè îò 3-é ãàðìîíèêè;
( )
( )
(
)
1
33
3
3
,
C
jC
UI
w
=
ãäå
( ) ( )
( )
21
3313
11
2
3
;
313
RjL
II
LC
Rj
+w
=
w-w
+
()
()
( )( )
( )
3
13
211
1
11
2
.
33
313
U
I
RjLjC
R
LC
Rj
=
+ww
+
w-w
+
Ïîñëå íàõîæäåíèÿ êîìïëåêñíûõ äåéñòâóþùèõ çíà÷åíèé íàïðÿæåíèé íà
åìêîñòè îòäåëüíûõ ãàðìîíèê è âûäåëåíèÿ â íèõ ìîäóëåé U
C(1)
, U
C(3)
è ôàç
j
C1
= arg U
C(1)
, j
C3
= arg U
C(3)
çàïèñûâàåò ìãíîâåííîå çíà÷åíèå íàïðÿæå-
íèÿ íà åìêîñòè â ôîðìå ñóììû (ðÿäà):
( )
( )
()
(
)
( )
(
)
1113
03
1
3
sinsin
CC
CCCC
tt
uUUU
t
w+jw+j
=++ .
Äåéñòâóþùåå çíà÷åíèå íàïðÿæåíèÿ îïðåäåëÿåì ñîãëàñíî (5.19)
( )
()
( )
222
03
1
.
CCCC
UUUU=++
Ïðè àíàëèçå ðåçîíàíñíûõ ÿâëåíèé â ýëåêòðè÷åñêèõ öåïÿõ ïðè
ïåðèîäè÷åñêèõ íåñèíóñîèäàëüíûõ âîçäåéñòâèÿõ ñëåäóåò èìåòü â
âèäó, ÷òî ðåçîíàíñ íàïðÿæåíèé è òîêîâ ìîæåò äîñòèãàòüñÿ íà ðàç-
íûõ ãàðìîíèêàõ. Ïðè ýòîì, êàê è ðàíåå, ðåçîíàíñîì íà k-é ãàð-
ìîíèêå íàçûâàåòñÿ òàêîå ñîñòîÿíèå ýëåêòðè÷åñêîé öåïè, ñîñòîÿùåé
èç ðàçíîõàðàêòåðíûõ ðåàêòèâíûõ ýëåìåíòîâ, ïðè êîòîðîì ôàçîâûé
ñäâèã ìåæäó âõîäíûì òîêîì è ïðèëîæåííûì íàïðÿæåíèåì k-x
ãàðìîíèê ðàâåí íóëþ. ßâëåíèå ðåçîíàíñà ìîæåò áûòü èñïîëüçîâàíî
äëÿ âûäåëåíèÿ îòäåëüíûõ ãàðìîíèê èç ïåðèîäè÷åñêîãî íåñèíóñîè-
ut
()
C
L
R
1
i
1
R
2
i
2
i
3
u
C
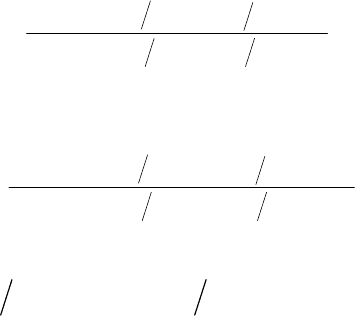
ut
()
i
1
L
1
i
2
i
C
1
C
2
Ðèñ. 5.6 Ðèñ. 5.7
156
äàëüíîãî ñèãíàëà. Ñëåäóåò ïîä÷åðêíóòü, ÷òî â öåïè ìîæåò îäíî-
âðåìåííî áûòü äîñòèãíóò ðåçîíàíñ òîêîâ íà îäíîé ÷àñòîòå è ðåçî-
íàíñ íàïðÿæåíèé íà äðóãîé.
Ïðèìåð. Äëÿ öåïè, èçîáðàæåííîé íà ðèñ. 5.7, ïðè çàäàííîé w
1
, L
1
íàéòè
çíà÷åíèå C
1
è C
2
, ïðè êîòîðûõ îäíîâðåìåííî âîçíèêàåò ðåçîíàíñ íàïðÿæåíèé
íà 1-é è ðåçîíàíñ òîêîâ íà 5-é ãàðìîíèêå. Èç óñëîâèÿ ðåçîíàíñà íàïðÿæåíèé
íàõîäèì, ÷òî âõîäíîå ðåàêòèâíîå ñîïðîòèâëåíèå öåïè íà ïåðâîé ãàðìîíèêå
äîëæíî ðàâíÿòüñÿ íóëþ:
( )
(
)
( )
1111
12
1
111112
1
1
0,
11
LC
C
j
X
LCC
j
w-w
×w
w
==
w-w-w
(5.32)
à íà ïÿòîé % áåñêîíå÷íîñòè (âõîäíàÿ ðåàêòèâíàÿ ïðîâîäèìîñòü íà ïÿòîé ãàð-
ìîíèêå äîëæíà áûòü ðàâíà íóëþ):
( )
(
)
( )
1111
12
1
111112
515
15
5
.
51515
LC
C
j
X
LCC
j
w-w
×w
w
==¥
w-w-w
(5.33)
Èç óñëîâèé (5.32) è (5.33) íàõîäèì èñêîìîå çíà÷åíèå åìêîñòåé:
(
)
(
)
22
12
1111
1;1.
24
CC
LL
==
ww
Âîïðîñû è çàäàíèÿ äëÿ ñàìîïðîâåðêè
1. Êàêîâà ìàòåìàòè÷åñêàÿ ìîäåëü ñïåêòðà ïåðèîäè÷åñêîãî íåñèíó-
ñîèäàëüíîãî ñèãíàëà?
2. Êàêîé âèä èìååò ñïåêòð ïåðèîäè÷åñêîãî íåãàðìîíè÷åñêîãî ñèã-
íàëà?
3. Êàê èçìåíÿåòñÿ ñïåêòð ïåðèîäè÷åñêîãî íåãàðìîíè÷åñêîãî ñèãíà-
ëà ïðè ñäâèãå íà÷àëà îòñ÷åòà çàäàííîé ôóíêöèè?
4. Êàê îïðåäåëèòü ñïåêòð ïåðèîäè÷åñêîé ôóíêöèè, çàäàííîé ãðà-
ôè÷åñêè?
5. Êàê îïðåäåëÿåòñÿ ñðåäíÿÿ çà ïåðèîä àêòèâíàÿ ìîùíîñòü ïåðèî-
äè÷åñêîãî íåãàðìîíè÷åñêîãî ñèãíàëà?
6. Êàê îïðåäåëÿåòñÿ è ÷òî õàðàêòåðèçóåò ìîùíîñòü èñêàæåíèé?
7. Êàê ðàññ÷èòûâàåòñÿ ñïåêòð êîìïëåêñíûõ àìïëèòóä ïîñëåäîâà-
òåëüíîñòè ïðÿìîóãîëüíûõ èìïóëüñîâ?
8. Êàê âëèÿåò ñêâàæíîñòü èìïóëüñîâ íà ñïåêòð ñèãíàëà?
9. Ðàññ÷èòàòü è ïîñòðîèòü ñïåêòð àìïëèòóä ïîñëåäîâàòåëüíîñòè
ïðÿìîóãîëüíûõ èìïóëüñîâ ñ ïàðàìåòðàìè: U
m
= 3Â, f = 0,5 êÃö
äëÿ äâóõ ñëó÷àåâ (q = 2, q = 5).
Îòâåò: 1) q = 2;
U
0
= 3 Â; U
m1
= 1,9 Â; U
m2
= 0; U
m3
= 0,64 Â;
U
m4
= 0; U
m5
= 0,38 Â; U
m6
= 0.
157
2) q = 5;
U
0
= 1,2 Â; U
m1
= 1,1 Â; U
m2
= 0,91 Â;
U
m3
= 0,6 Â; U
m4
= 0,28 Â; U
m5
= 0;
U
m6
= 0,19 Â; U
m7
= 0,25 Â; U
m8
= 0,23 Â;
U
m9
= 0,12 Â; U
m10
= 0.
10. Êàêîâ àëãîðèòì ðàñ÷åòà ëèíåéíûõ ýëåêòðè÷åñêèõ öåïåé, íàõî-
äÿùèõñÿ ïîä âîçäåéñòâèåì ïåðèîäè÷åñêèõ íåãàðìîíè÷åñêèõ ñè-
ãíàëîâ?
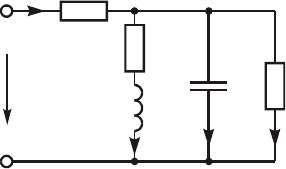
11. Íà âõîä öåïè, èçîáðàæåííîé íà
ðèñ. 5.8, ïîñòóïàåò ïåðèîäè÷åñêèé
íåãàðìîíè÷åñêèé ñèãíàë u(t) = U
0
+
+ U
m1
sinw
1
t + U
m3
sin(3w
1
t + j
3
);
U
0
= 30 Â; U
m1
=
100 Â; U
m3
=
40 Â;
j
3
= 20°. Ïàðàìåòðû ýëåìåíòîâ öåïè
íà îñíîâíîé ÷àñòîòå èçâåñòíû: w
1
L =
= 12 Îì; 1/(w
1
Ñ) = 30 Îì; R
1
= 6 Îì;
R
2
= 5 Îì; R
3
= 20 Îì. Ðàññ÷èòàòü:
1) òîê â íåðàçâåòâëåííîé ÷àñòè ñõåìû è çàïèñàòü åãî ìãíîâåí-
íîå çíà÷åíèå; 2) äåéñòâóþùèå çíà÷åíèÿ âñåõ òîêîâ; 3) àêòèâ-
íóþ ìîùíîñòü, ïîòðåáëÿåìóþ öåïüþ.
Îòâåò: 1) i
1
(t) = 3 + 5,88sin(w
1
t $ 16°30¢) +
+ 2,6sin(3w
1
t + 55°), A.
2) I
1
= 5,45 À; I
2
= 4,4 À; I
3
= 2,64 À; I
4
= 2,57 À.
3) P = 415 Âò.
12. Ðåçîíàíñíûå ÿâëåíèÿ â ëèíåéíûõ ýëåêòðè÷åñêèõ öåïÿõ ïðè íå-
ãàðìîíè÷åñêèõ ïåðèîäè÷åñêèõ âîçäåéñòâèÿõ.
13. Äëÿ öåïè èçîáðàæåííîé íà ðèñ. 5.7, íàéòè çíà÷åíèÿ Ñ
1
è Ñ
2
,
ïðè êîòîðûõ îäíîâðåìåííî âîçíèêàåò ðåçîíàíñ íàïðÿæåíèé íà
1-îé ãàðìîíèêå è ðåçîíàíñ òîêîâ íà 5-îé ãàðìîíèêå, åñëè çàäàíû
L
1
= 10 ìÃí; w
1
= 5×10
3
ðàä/ñ.
Îòâåò: Ñ
1
= 4 ìêÔ; Ñ
2
= 0,167 ìêÔ.
ÃËÀÂÀ 6. ÏÅÐÅÕÎÄÍÛÅ ÏÐÎÖÅÑÑÛ Â ËÈÍÅÉÍÛÕ
ÝËÅÊÒÐÈ×ÅÑÊÈÕ ÖÅÏßÕ. ÊËÀÑÑÈ×ÅÑÊÈÉ
ÌÅÒÎÄ ÀÍÀËÈÇÀ
6.1. Ïåðåõîäíûé ðåæèì ýëåêòðè÷åñêèõ öåïåé.
Çàêîíû êîììóòàöèè
 ïðåäûäóùèõ ãëàâàõ ðàññìàòðèâàëèñü ïðîöåññû â ýëåêòðè÷å-
ñêèõ öåïÿõ è ìåòîäû èõ ðàñ÷åòà â óñòàíîâèâøåìñÿ ðåæèìå, ò. å. â
ðåæèìå, ïðè êîòîðîì íàïðÿæåíèÿ è òîêè â öåïÿõ ëèáî íå çàâèñÿò
R
2
R
1
L
i
2
C
R
3
i
1
i
4
i
3
ut
()
Ðèñ. 5.8

158
îò âðåìåíè, ëèáî ÿâëÿþòñÿ ïåðèîäè÷åñêèìè ôóíêöèÿìè âðåìåíè â
çàâèñèìîñòè îò âèäà ïðèëîæåííîãî âîçäåéñòâèÿ. Óñòàíîâèâøèéñÿ
ðåæèì â öåïè äîñòèãàåòñÿ îáû÷íî ÷åðåç îïðåäåëåííûé ïðîìåæóòîê
âðåìåíè ïîñëå íà÷àëà âîçäåéñòâèÿ, ïîýòîìó ðàññìîòðåííûå ðàíåå
ìåòîäû àíàëèçà íå îõâàòûâàþò òàê íàçûâàåìûé ïåðåõîäíûé ðåæèì
îò íà÷àëà âîçäåéñòâèÿ äî óñòàíîâèâøåãîñÿ ñîñòîÿíèÿ öåïè. Ïåðå-
õîäíîé ðåæèì ðàáîòû öåïè îáóñëîâëåí íàëè÷èåì â íåé ðåàêòèâíûõ
ýëåìåíòîâ (èíäóêòèâíîñòè, åìêîñòè), â êîòîðûõ íàêàïëèâàåòñÿ
ýíåðãèÿ ìàãíèòíîãî è ýëåêòðè÷åñêîãî ïîëåé. Ïðè ðàçëè÷íîãî ðîäà
âîçäåéñòâèÿõ (ïîäêëþ÷åíèè ê öåïè èëè èñêëþ÷åíèè èñòî÷íèêîâ
ýëåêòðè÷åñêîé ýíåðãèè, èçìåíåíèè ïàðàìåòðîâ öåïè) èçìåíÿåòñÿ
ýíåðãåòè÷åñêèé ðåæèì ðàáîòû öåïè, ïðè÷åì ýòè èçìåíåíèÿ íå ìî-
ãóò îñóùåñòâëÿòüñÿ ìãíîâåííî â ñèëó íåïðåðûâíîñòè èçìåíåíèÿ
ýíåðãèè ýëåêòðè÷åñêîãî è ìàãíèòíîãî ïîëåé (ïðèíöèï íåïðåðûâíî-
ñòè), ÷òî è ïðèâîäèò ê âîçíèêíîâåíèþ ïåðåõîäíûõ ïðîöåññîâ.
Ñëåäóåò ïîä÷åðêíóòü, ÷òî ïåðåõîäíûå ïðîöåññû âî ìíîãèõ óñòðîé-
ñòâàõ è ñèñòåìàõ ñâÿçè ÿâëÿþòñÿ ñîñòàâíîé «íîðìàëüíîé» ÷àñòüþ
ðåæèìà èõ ðàáîòû.  òî æå âðåìÿ â ðÿäå ñëó÷àåâ ïåðåõîäíûå ïðî-
öåññû ìîãóò ïðèâîäèòü ê òàêèì íåæåëàòåëüíûì ÿâëåíèÿì, êàê âîç-
íèêíîâåíèå ñâåðõòîêîâ è ïåðåíàïðÿæåíèé. Âñå ýòî îïðåäåëÿåò
âàæíîñòü ðàññìîòðåíèÿ ìåòîäîâ àíàëèçà ïåðåõîäíûõ ïðîöåññîâ â
ýëåêòðè÷åñêèõ öåïÿõ.
 îñíîâå ìåòîäîâ ðàñ÷åòà ïåðåõîäíûõ ïðîöåññîâ ëåæàò çàêîíû
êîììóòàöèè. Êîììóòàöèåé ïðèíÿòî íàçûâàòü ëþáîå èçìåíåíèå
ïàðàìåòðîâ öåïè, åå êîíôèãóðàöèè, ïîäêëþ÷åíèå èëè îòêëþ÷åíèå
èñòî÷íèêîâ, ïðèâîäÿùåå ê âîçíèêíîâåíèþ ïåðåõîäíûõ ïðîöåññîâ.
Êîììóòàöèþ áóäåì ñ÷èòàòü ìãíîâåííîé, îäíàêî ïåðåõîäíûé ïðî-
öåññ, êàê áûëî îòìå÷åíî âûøå, áóäåò ïðîòåêàòü îïðåäåëåííîå âðå-
ìÿ. Òåîðåòè÷åñêè äëÿ çàâåðøåíèÿ ïåðåõîäíîãî ïðîöåññà òðåáóåòñÿ
áåñêîíå÷íî áîëüøîå âðåìÿ, íî íà ïðàêòèêå åãî ïðèíèìàþò êîíå÷-
íûì, çàâèñÿùèì îò ïàðàìåòðîâ öåïè. Áóäåì ñ÷èòàòü, ÷òî êîììó-
òàöèÿ îñóùåñòâëÿåòñÿ ñ ïîìîùüþ èäåàëüíîãî êëþ÷à Ê (ðèñ. 6.1),
ñîïðîòèâëåíèå êîòîðîãî â ðàçîìêíóòîì ñîñòîÿíèè áåñêîíå÷íî âå-
ëèêî, à â çàìêíóòîì ðàâíî íóëþ. Íàïðàâëåíèå çàìûêàíèÿ èëè
ðàçìûêàíèÿ êëþ÷à áóäåì ïîêàçûâàòü ñòðåëêîé. Áóäåì òàêæå ñ÷è-
òàòü, åñëè íå îãîâîðåíî èíîå, ÷òî êîììóòàöèÿ îñóùåñòâëÿåòñÿ â
ìîìåíò t = 0.
Ðàçëè÷àþò ïåðâûé è âòîðîé çàêîíû êîììóòàöèè. Ïåðâûé çàêîí
êîììóòàöèè ñâÿçàí ñ íåïðåðûâíîñòüþ èçìåíåíèÿ ìàãíèòíîãî ïîëÿ
êàòóøêè èíäóêòèâíîñòè W
L
= Li
2
/2 è ãëàñèò: â íà÷àëüíûé ìîìåíò
t = 0
+
íåïîñðåäñòâåííî ïîñëå êîììóòàöèè òîê â èíäóêòèâíîñòè
èìååò òî æå çíà÷åíèå, ÷òî è â ìîìåíò t = 0
$
äî êîììóòàöèè è
ñ ýòîãî ìîìåíòà ïëàâíî èçìåíÿåòñÿ
*
*
Çäåñü è äàëåå ïîä f (0
$
) ïîíèìàåòñÿ ëåâîñòîðîííèé ïðåäåë ôóíêöèè f (t) ïðè t ® 0
$
,
à ïîä f (0
+
) %ïðàâîñòîðîííèé ïðåäåë f (t) ïðè t ® 0
+
.
159
(
)
(
)
.
00
LL
ii
-+
=
(6.1)
Âòîðîé çàêîí êîììóòàöèè ñâÿçàí ñ íåïðåðûâíîñòüþ èçìåíå-
íèÿ ýëåêòðè÷åñêîãî ïîëÿ åìêîñòè W
C
= Cu
2
/2; â íà÷àëüíûé ìî-
ìåíò t = 0
+
íåïîñðåäñòâåííî ïîñëå êîììóòàöèè íàïðÿæåíèå íà
åìêîñòè èìååò òî æå çíà÷åíèå, ÷òî è â ìîìåíò: t = 0
$
äî êîì-
ìóòàöèè è ñ ýòîãî ìîìåíòà ïëàâíî èçìåíÿåòñÿ:
(
)
(
)
.
00
CC
uu
-+
=
(6.2)
 îòëè÷èå îò òîêà â èíäóêòèâíîñòè i
L
è íàïðÿæåíèÿ íà åìêîñòè
u
C
íàïðÿæåíèå íà èíäóêòèâíîñòè u
L
è òîê â åìêîñòè i
C
ìîãóò èç-
ìåíÿòüñÿ ñêà÷êîì, òàê êàê ñîãëàñíî (1.9) è (1.12) îíè ÿâëÿþòñÿ
ïðîèçâîäíûìè îò i
L
è u
C
è ñ íèìè íåïîñðåäñòâåííî íå ñâÿçàíà
ýíåðãèÿ ìàãíèòíîãî è ýëåêòðè÷åñêîãî ïîëåé. Çíà÷åíèÿ òîêîâ â èí-
äóêòèâíîñòè i
L
(0
+
) è íàïðÿæåíèé íà åìêîñòÿõ u
C
(0
+
) îáðàçóþò íà-
÷àëüíûå óñëîâèÿ çàäà÷è.  çàâèñèìîñòè îò íà÷àëüíîãî ýíåðãå-
òè÷åñêîãî ñîñòîÿíèÿ öåïè ðàçëè÷àþò äâà òèïà çàäà÷ ðàñ÷åòà ïå-
ðåõîäíûõ ïðîöåññîâ: çàäà÷è ñ íóëåâûìè íà÷àëüíûìè óñëîâèÿìè,
êîãäà íåïîñðåäñòâåííî ïîñëå êîììóòàöèè (ïðè t = 0
+
) i
L
(0
+
) = 0;
u
C
(0
+
) = 0 (ò. å. W
L
(0
+
) + W
C
(0
+
) = 0) è çàäà÷è ñ íåíóëåâûìè
íà÷àëüíûìè óñëîâèÿìè, êîãäà i
L
(0
+
) ¹ 0 è (èëè) u
C
(0
+
) ¹ 0 (ò. å.
W
L
(0
+
) + W
C
(0
+
) ¹ 0). Íóëåâûå è íåíóëåâûå çíà÷åíèÿ íà÷àëüíûõ
óñëîâèé äëÿ i
L
è u
C
íàçûâàþòñÿ íåçàâèñèìûìè, à íà÷àëüíûå óñ-
ëîâèÿ îñòàëüíûõ òîêîâ è íàïðÿæåíèé çàâèñèìûìè. Íåçàâèñèìûå
íà÷àëüíûå óñëîâèÿ îïðåäåëÿþòñÿ ñ ïîìîùüþ çàêîíîâ êîììóòàöèè
(6.1) è (6.2).
6.2. Êëàññè÷åñêèé ìåòîä ðàñ÷åòà ïåðåõîäíûõ ïðîöåññîâ
 îñíîâå êëàññè÷åñêîãî ìåòîäà ðàñ÷åòà ïåðåõîäíûõ ïðîöåññîâ â
ýëåêòðè÷åñêèõ öåïÿõ ëåæèò ñîñòàâëåíèå èíòåãðàëüíî-äèôôåðåí-
öèàëüíûõ óðàâíåíèé äëÿ ìãíîâåííûõ çíà÷åíèé òîêîâ è íàïðÿæå-
íèé. Ýòè óðàâíåíèÿ ñîñòàâëÿþòñÿ íà îñíîâå çàêîíîâ Êèðõãîôà,
ìåòîäîâ êîíòóðíûõ òîêîâ, óçëîâûõ íàïðÿæåíèé è ìîãóò ñîäåðæàòü
êàê íåçàâèñèìûå, òàê è çàâèñèìûå ïåðåìåííûå. Äëÿ óäîáñòâà ðå-
øåíèÿ îáû÷íî ïðèíÿòî ñîñòàâëÿòü äèôôåðåíöèàëüíûå óðàâíåíèÿ
îòíîñèòåëüíî íåçàâèñèìîé ïåðåìåííîé, â êà÷åñòâå êîòîðîé ìîæåò
ñëóæèòü i
L
èëè u
C
. Ðåøåíèå ïîëó÷åííûõ äèôôåðåíöèàëüíûõ
óðàâíåíèé îòíîñèòåëüíî âûáðàííîé ïåðåìåííîé è ñîñòàâëÿåò ñóù-
íîñòü êëàññè÷åñêîãî ìåòîäà.
Ó÷èòûâàÿ, ÷òî â ðÿäå ñëó÷àåâ ðåøåíèå äèôôåðåíöèàëüíûõ
óðàâíåíèé ïðîùå èíòåãðàëüíî-äèôôåðåíöèàëüíûõ, ïîëó÷åííóþ ñè-
ñòåìó ñâîäÿò ê îäíîìó äèôôåðåíöèàëüíîìó óðàâíåíèþ ñîîòâåòñò-
âóþùåãî ïîðÿäêà îòíîñèòåëüíî âûáðàííîé íåçàâèñèìîé ïåðåìåí-
íîé i
L
èëè u
C
. Ïîðÿäîê äèôôåðåíöèàëüíîãî óðàâíåíèÿ îïðåäåëÿ-

160
åòñÿ ÷èñëîì íåçàâèñèìûõ íàêîïèòåëåé ýíåðãèè ýëåêòðè÷åñêîãî è
ìàãíèòíîãî ïîëåé.
Îáîçíà÷èì íåçàâèñèìóþ ïåðåìåííóþ (i
L
èëè u
C
) ÷åðåç x = x(t).
Äèôôåðåíöèàëüíîå óðàâíåíèå m-ão ïîðÿäêà, îïèñûâàþùåå ïå-
ðåõîäíûé ïðîöåññ â ýëåêòðè÷åñêîé öåïè, íàõîäÿùåéñÿ ïîä âîçäåé-
ñòâèåì èñòî÷íèêà w(t), îïèñûâàåòñÿ óðàâíåíèåì:
()
1
110
1
,
mm
mm
mm
dxdxdx
bbbbxw
t
dtdtdt
-
-
-
++++=K (6.3)
ãäå b
0
, b
1
, ..., b
m$1
, b
ò
% êîýôôèöèåíòû ïàðàìåòðîâ öåïè; w(t) %
ôóíêöèÿ, îïèñûâàþùàÿ õàðàêòåð âîçäåéñòâèÿ íà öåïü.
Öåïü, ïàðàìåòðû êîòîðîé b
0
, b
1
, ..., b
m$1
, b
ò
íåèçìåííû, íà-
çûâàþò öåïüþ ñ ïîñòîÿííûìè ïàðàìåòðàìè. Åñëè æå êàêîé-ëèáî
èç êîýôôèöèåíòîâ b
0
, b
1
, ..., b
m$1
, b
ò
% ïåðåìåíåí, òî öåïü íàçû-
âàþò ïàðàìåòðè÷åñêîé.  äàëüíåéøåì áóäåì ðàññìàòðèâàòü öåïè ñ
ïîñòîÿííûìè ïàðàìåòðàìè.
Äèôôåðåíöèàëüíîå óðàâíåíèå (6.3) îòíîñèòñÿ ê ëèíåéíûì íå-
îäíîðîäíûì óðàâíåíèÿì ò-ãî ïîðÿäêà. Êàê èçâåñòíî, åãî ðåøåíèå
íàõîäèòñÿ êàê ñóììà îáùåãî ðåøåíèÿ x
ñâ
îäíîðîäíîãî äèôôåðåí-
öèàëüíîãî óðàâíåíèÿ m-ãî ïîðÿäêà:
1
ñâ ñâ ñâ
110ñâ
1
0
mm
mm
mm
dxdxdx
bbbbx
dtdtdt
-
-
-
++++=
K (6.4)
è ÷àñòíîãî ðåøåíèÿ x
ïð
óðàâíåíèÿ (6.3):
ïðñâ
xxx
=+
, (6.5)
ãäå x
ñâ
è x
ïð
% îáùåå è ÷àñòíîå ðåøåíèÿ. Îáùåå ðåøåíèå x
ñâ
îï-
ðåäåëÿåò ñâîáîäíûå ïðîöåññû, êîòîðûå ïðîòåêàþò â öåïè áåç ó÷à-
ñòèÿ èñòî÷íèêà w(t) (îòñþäà èíäåêñ «ñâ»). ×àñòíîå ðåøåíèå x
ïð
îïðåäåëÿåò ïðèíóäèòåëüíûé ïðîöåññ (îòñþäà èíäåêñ «ïð»), êîòî-
ðûé ïðîòåêàåò â öåïè ïîä âëèÿíèåì w(t). Â òåîðèè öåïåé x
ïð
îáû÷íî íàõîäÿò îäíèì èç ðàíåå ðàññìîòðåííûõ ìåòîäîâ ðàñ÷åòà
öåïåé â óñòàíîâèâøåìñÿ ðåæèìå.
Ñâîáîäíàÿ ñîñòàâëÿþùàÿ ïåðåõîäíîãî ïðîöåññà x
ñâ
áóäåò çà-
âèñåòü îò õàðàêòåðà êîðíåé õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ:
1
110
0.
mm
mm
bpbpbpb
-
-
++++=
K
(6.6)
 ñëó÷àå, êîãäà êîðíè p
1
, p
2
, ..., ð
ò
õàðàêòåðèñòè÷åñêîãî óðàâ-
íåíèÿ (6.6) âåùåñòâåííûå è ðàçëè÷íûå, ðåøåíèå (6.4) èìååò âèä
12
ñâ12
.
m
ptptpt
m
xAeAeAe=+++
K
(6.7)
ãäå A
1
, A
2
, ..., A
ò
% ïîñòîÿííûå èíòåãðèðîâàíèÿ, êîòîðûå íàõî-
äÿòñÿ èç íà÷àëüíûõ óñëîâèé.
 ñëó÷àå, êîãäà êîðíè óðàâíåíèÿ (6.6) âåùåñòâåííûå è ðàâíûå,
ò. å. p
1
= p
2
= ... = ð
ò
= p, ñâîáîäíàÿ ñîñòàâëÿþùàÿ îïðåäåëÿåòñÿ
óðàâíåíèåì
