Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.


141
Схема, изображенная на рис. 4.33 полностью описывается следующей таблицей со-
единений:
1
R
; 1, 2; 100
1
L
; 2, 3; 0.0001
2
R
; 3, 0; 200
Первый символ указывает тип (R, L, C) и порядковый номер элемента ветви. Вто-
рая и третья цифры в спецификации указывают номера узлов, между которыми включен
элемент. Последняя цифра характеризует значение параметра.
2. Ðàñ÷åò ïåðåäàòî÷íîé ôóíêöèè öåïè. Приведем последовательность расчета пе-
редаточной функции цепи с использованием метода узловых напряжений:
- По введенной в ЭВМ схеме определяется структурная матрица
0
A
.
- Формируются матрицы эдс источников напряжения
â
E
r
и проводимостей ветвей
â
Y
.
- Формируется матрица узловых проводимостей
y
Y
.
- Формируется матрица узловых токов
y
I
r
.
- Определяется матрица узловых напряжений:
1
yyy
-
=×
VYI
rr
.
- Положив
âõ
U
= 1 В, определяется матрица комплексной передаточной функции
yy
=
HV
rr
.
- Рассчитываются и строятся графики АЧХ
(
)
(
)
fH и ФЧХ
(
)
(
)
í
f
j .
Структурная матрица
0
110
011
-
éù
=
êú
-
ëû
A
.
Матрица эдс источников напряжения
âõ
â
0
0
U
éù
êú
=
êú
ëû
E
r
.
Матрица проводимостей ветвей.
( )
â
100
010
001
R
jL
R
éù
êú
=
w
êú
ëû
Y .
Матрица узловых токов
( )
( )
âõ
y0ââ
100
110
0100
011
0
001
U
R
jL
R
æö
éù
éù
-
éù
ç÷
êú
êú
=-=×-
w
êú
-
ç÷
êú
êú
ëû
ëû
ëû
èø
IAYE
rr
;
âõ
y
0
UR
éù
=
êú
ëû
I
r
.
Матрица узловых проводимостей
( )
T
y0â0
10010
110
01011
011
01
001
R
jL
R
-
éù
éù
-
éù
êú
êú
==×-
w
êú
-
êú
êú
ëû
ëû
ëû
YAYA ;
y
111
111
RjLjL
jLRjL
éù
+-
êú
ww
=
êú
êú
-+
êú
ww
ëû
Y .
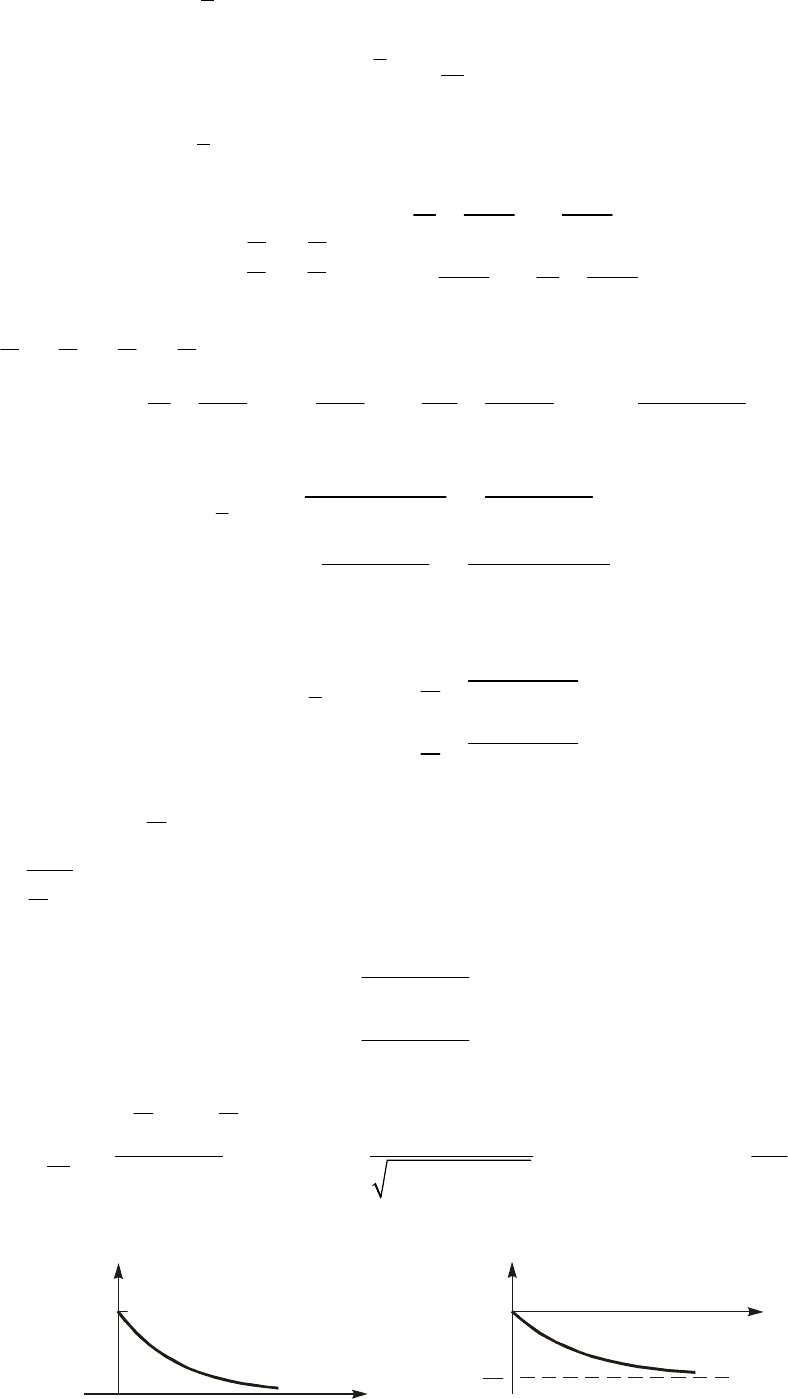
142
H
u
j
í
0,5
w
w
0
0
2
p
-
Ðèñ. 4.34
Обратная матрица
1
y
-
Y
1
y
-
=
D
A
Y
%
,
где
A
%
– присоединенная матрица,
D – определитель
y
Y
.
1121
1222
111
111
AA
RjLjL
AA
jLRjL
éù
+
êú
ww
éù
==
êú
êú
ëû
êú
+
êú
ww
ëû
A
%
,
где
11122122
,,,
AAAA
– алгебраические дополнения.
22
2
11112
RjLjLjLR
R
æöæö
D=+-=+
ç÷ç÷
www
èøèø
.
2
2
RjL
jLR
+w
D=
w
.
(
)
( )
2
1
y
2
22
22
RRjL
R
RjLRjL
RRjL
R
RjLRjL
-
éù
+w
êú
+w+w
êú
=
+w
êú
êú
+w+w
ëû
Y .
Матрица узловых напряжений
âõ
1
yyy
âõ
2
2
RjL
U
RjL
R
U
RjL
-
+w
éù
êú
+w
==
êú
êú
êú
+w
ëû
VYI
rr
.
Ïðèíèìàåì
âõ
U
= 1  è íàõîäèì ïåðåäàòî÷íóþ ôóíêöèþ ïî íàïðÿæåíèþ:
y
âõ
u
U
=
V
H
r
r
.
( )
( )
Óçëû
2
2
3
2
u
RjL
RjL
R
RjL
+w
éù
êú
+w
=
êú
êú
êú
+w
ëû
H
r
.
На рис. 4.33
âûõ3
UV
=
, следовательно,
2
u
R
H
RjL
=
+w
;
( )
( )
2
2
4
u
R
H
RL
w=
+w
;
( )
arctg
2
u
L
R
w
jw=-
.
143
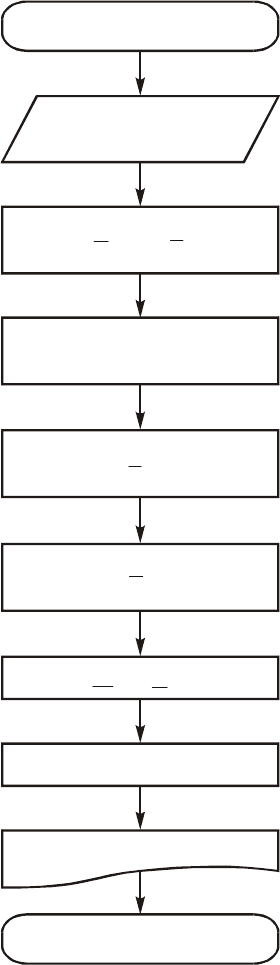
Ôîðìèðîâàíèå ìàòðèö
â
0
E
,
Y
,
A
r
y
1
yy
I
Y
V
r
r
×
=
-
Çàäàíèå ñõåìû,
n,1U
âõ
=
n
u
V
H
=
Ðàñ÷åò À×Õ, Ô×Õ
Íà÷àëî
Êîíåö
â
Ôîðìèðîâàíèå ìàòðèöû
ó
I
r
Âûâîä À×Õ è Ô×Õ
Ôîðìèðîâàíèå
ó
Y
Ôîðìèðîâàíèå
Ðèñ. 4.35
На рис. 4.34 приведены графики АЧХ –
(
)
u
H
w
и ФЧХ –
(
)
u
jw
.
3. Àëãîðèòì ðàñ÷åòà À×Õ è Ô×Õ. На рис. 4.35 приведен алгоритм расчета АЧХ и
ФЧХ цепи на основе метода узловых напряжений.
Âîïðîñû è çàäàíèÿ äëÿ ñàìîïðîâåðêè
1. ×òî òàêîå À×Õ è Ô×Õ öåïè, åñëè ðàññìàòðèâàåòñÿ åå êîìïëåêñ-
íàÿ ïåðåäàòî÷íàÿ ôóíêöèÿ ïî íàïðÿæåíèþ?
2. Ïî÷åìó ðåçîíàíñ â ïîñëåäîâàòåëüíîì êîëåáàòåëüíîì êîíòóðå íà-
çûâàåòñÿ ðåçîíàíñîì íàïðÿæåíèé?
3. ×òî òàêîå äîáðîòíîñòü êîëåáàòåëüíîãî êîíòóðà?
4. ×òî òàêîå ïîëîñà ïðîïóñêàíèÿ êîëåáàòåëüíîãî êîíòóðà?

144
5. Ïî÷åìó ðåçîíàíñ â ïàðàëëåëüíîì êîëåáàòåëüíîì êîíòóðå íàçû-
âàåòñÿ ðåçîíàíñîì òîêîâ?
6. Êàêîâû ýêâèâàëåíòíûå ñõåìû ïîñëåäîâàòåëüíîãî è ïàðàëëåëüíî-
ãî êîíòóðîâ íà ðåçîíàíñíîé ÷àñòîòå?
7. Ïî÷åìó ïîñëåäîâàòåëüíûé êîíòóð äîëæåí ðàáîòàòü ñ èñòî÷íèêîì
ñèãíàëà, èìåþùèì ìàëîå âíóòðåííåå ñîïðîòèâëåíèå, à ïàðàë-
ëåëüíûé êîíòóð $ ñ èñòî÷íèêîì, èìåþùèì áîëüøîå âíóòðåííåå
ñîïðîòèâëåíèå?
8.  ÷åì çàêëþ÷àåòñÿ äîñòîèíñòâî ñâÿçàííûõ êîëåáàòåëüíûõ êîí-
òóðîâ ïî ñðàâíåíèþ ñ îäèíî÷íûì?
9. Êàêîâû îñíîâíûå ñâîéñòâà ðåàêòèâíûõ äâóõïîëþñíèêîâ?
10. Êà÷åñòâåííî ïîñòðîèòü À×Õ öåïåé, ïîëó÷àåìûõ íà ðèñóíêå 4.36.
11. Ïîñëåäîâàòåëüíûé êîëåáàòåëüíûé êîíòóð, èìåþùèé L =
= 100 ìêÃí, C= 2,5 íÔ, R = 6 Îì, ðàáîòàåò ñ èñòî÷íèêîì ñèã-
íàëà, ó êîòîðîãî R
ã
= 2 Îì. Êàêîâà áóäåò ïîëîñà ïðîïóñêàíèÿ
ñèñòåìû äî è ïîñëå ïîäêëþ÷åíèÿ íàãðóçêè ê åìêîñòíîìó ýëå-
ìåíòó ñ ñîïðîòèâëåíèåì R
í
= 10 êÎì?
Îòâåò: Df
à
= 12,7 êÃö $ íåíàãðóæåííîãî è
Df
à.í
= 19,1 êÃö $ íàãðóæåííîãî êîíòóðîâ.
ÃËÀÂÀ 5. ËÈÍÅÉÍÛÅ ÝËÅÊÒÐÈ×ÅÑÊÈÅ ÖÅÏÈ Â
ÐÅÆÈÌÅ ÏÅÐÈÎÄÈ×ÅÑÊÈÕ ÍÅÃÀÐÌÎÍÈ×ÅÑÊÈÕ
ÂÎÇÄÅÉÑÒÂÈÉ
5.1. Íåãàðìîíè÷åñêèå ïåðèîäè÷åñêèå ñèãíàëû.
Ðàçëîæåíèå â ðÿä Ôóðüå
Ïðè ïåðåäà÷å èíôîðìàöèè ïî êàíàëàì ñâÿçè â ïðîöåññå ïðå-
îáðàçîâàíèÿ ñèãíàëîâ â ðàçëè÷íûõ óñòðîéñòâàõ, êàê ïðàâèëî, èñ-
ïîëüçóþò íåãàðìîíè÷åñêèå êîëåáàíèÿ, ïîñêîëüêó ÷èñòî ãàðìîíè-
÷åñêèå êîëåáàíèÿ íå ìîãóò ÿâëÿòüñÿ íîñèòåëÿìè èíôîðìàöèè. Äëÿ
ïåðåäà÷è ñîîáùåíèé îñóùåñòâëÿþò ìîäóëÿöèþ ãàðìîíè÷åñêîãî êî-
ëåáàíèÿ ïî àìïëèòóäå $ àìïëèòóäíàÿ ìîäóëÿöèÿ (AM), ÷àñòîòå $
L
C
R
2
R
1
R
2
R
1
R
2
R
1
C
R
2
R
1
L
a
)
á
)
â
)
ã
)
Ðèñ. 4.36
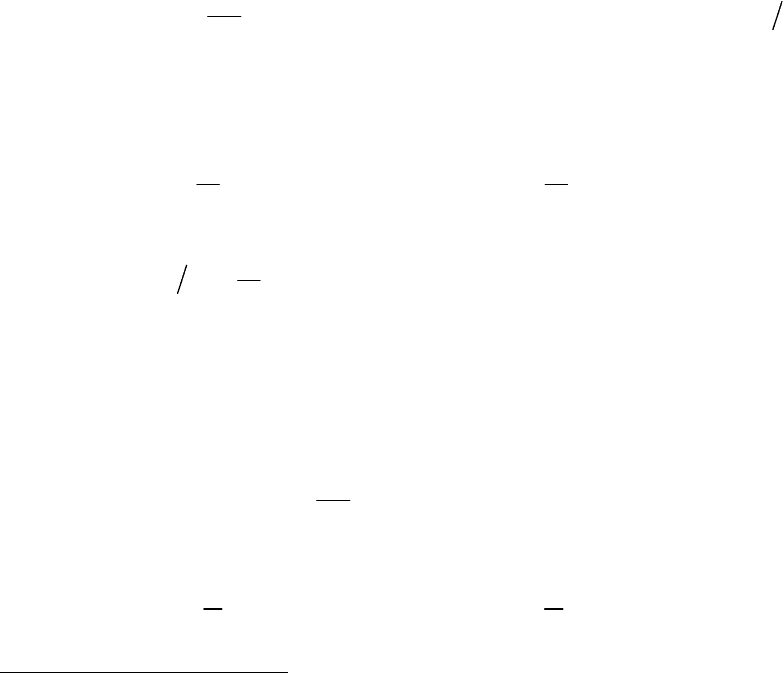
145
÷àñòîòíàÿ ìîäóëÿöèÿ (×Ì) èëè ôàçå $ ôàçîâàÿ ìîäóëÿöèÿ (ÔÌ),
ëèáî èñïîëüçóþò èìïóëüñíûå ñèãíàëû, ìîäóëèðóåìûå ïî àìïëè-
òóäå $ àìïëèòóäíî-èìïóëüñíàÿ ìîäóëÿöèÿ (ÀÈÌ), øèðèíå $ øè-
ðîòíî-èìïóëüñíàÿ ìîäóëÿöèÿ (ØÈÌ), âðåìåííîìó ïîëîæåíèþ $
âðåìÿ-èìïóëüñíàÿ ìîäóëÿöèÿ (ÂÈÌ). Ñóùåñòâóþò è äðóãèå, áîëåå
ñëîæíûå ñèãíàëû, ôîðìèðóåìûå ïî ñïåöèàëüíûì çàêîíàì. Îòëè-
÷èòåëüíîé ÷åðòîé óêàçàííûõ ñèãíàëîâ ÿâëÿåòñÿ ñëîæíûé íåãàðìî-
íè÷åñêèé õàðàêòåð. Íåñèíóñîèäàëüíûé âèä èìåþò òîêè è íàïðÿæå-
íèÿ, ôîðìèðóåìûå â ðàçëè÷íûõ èìïóëüñíûõ è öèôðîâûõ óñòðîé-
ñòâàõ (ãë. 19), íåñèíóñîèäàëüíûé õàðàêòåð ïðèîáðåòàþò ãàðìîíè-
÷åñêèå ñèãíàëû, ïðîõîäÿùèå ÷åðåç ðàçëè÷íûå íåëèíåéíûå óñòðîé-
ñòâà (ãë. 11) è ò. ä. Âñå ýòî ïðèâîäèò ê íåîáõîäèìîñòè ðàçðàáîòêè
ñïåöèàëüíûõ ìåòîäîâ àíàëèçà è ñèíòåçà ýëåêòðè÷åñêèõ öåïåé, íà-
õîäÿùèõñÿ ïîä âîçäåéñòâèåì ïåðèîäè÷åñêèõ íåñèíóñîèäàëüíûõ è
íåïåðèîäè÷åñêèõ òîêîâ è íàïðÿæåíèé.  îñíîâå ýòèõ ìåòîäîâ ëå-
æàò ñïåêòðàëüíûå ïðåäñòàâëåíèÿ íåñèíóñîèäàëüíûõ âîçäåéñòâèé,
áàçèðóþùèåñÿ íà ðàçëîæåíèè â ðÿä èëè èíòåãðàë Ôóðüå.
Èç ìàòåìàòè÷åñêîãî àíàëèçà èçâåñòíî, ÷òî ïåðèîäè÷åñêàÿ íå-
ãàðìîíè÷åñêàÿ ôóíêöèÿ f(t) óäîâëåòâîðÿþùàÿ óñëîâèÿì Äèðèõëå
*
,
ìîæåò áûòü ðàçëîæåíà â ðÿä Ôóðüå:
()
( )
0
11
1
1
cossin
;2,
2
kk
k
a
aktbkt
fT
t
¥
=
w+w
=+w=p
å
(5.1)
ãäå a
k
, b
k
% êîýôôèöèåíòû ðàçëîæåíèÿ, îïðåäåëÿåìûå óðàâíå-
íèÿìè
() ()
11
00
22
cos;sin.
TT
kk
afktdtbfktdt
tt
TT
=w=w
òò
(5.2)
Âåëè÷èíà
()
0
0
1
2
T
afdt
t
T
=
ò
ïðåäñòàâëÿåò ñðåäíåå çà ïåðèîä çíà÷å-
íèå ôóíêöèè f(t)
**
è íàçûâàåòñÿ ïîñòîÿííîé ñîñòàâëÿþùåé.
 òåîðåòè÷åñêèõ èññëåäîâàíèÿõ îáû÷íî âìåñòî ôîðìóëû (5.1)
èñïîëüçóþò äðóãóþ, îñíîâàííóþ íà çàìåíå íåçàâèñèìîé ïåðåìåí-
íîé a = w
1
t:
( )
( )
0
1
,
cossin
2
kk
k
a
f
akbk
¥
=
a=+
a+a
å
(5.3)
ãäå
( ) ( )
22
00
11
cos;sin.
kk
afkdbfkd
pp
=aaa=aaa
pp
òò
(5.4)
*
Ýòè óñëîâèÿ òðåáóþò, ÷òîáû íà ïåðèîäå Ò ôóíêöèÿ f (t) èìåëà êîíå÷íîå ÷èñëî ðàç-
ðûâîâ ïåðâîãî ðîäà è êîíå÷íîå ÷èñëî ìàêñèìóìîâ è ìèíèìóìîâ, ÷òî äëÿ ðåàëüíûõ
ýëåêòðè÷åñêèõ ñèãíàëîâ îáû÷íî âûïîëíÿåòñÿ.
**
Ôóíêöèÿ f (t) ìîæåò èìåòü ñìûñë êàê òîêà, òàê è íàïðÿæåíèÿ.

146
Óðàâíåíèå (5.3) åñòü òðèãîíîìåòðè÷åñêàÿ ôîðìà ðÿäà Ôóðüå.
Ïðè àíàëèçå öåïåé ÷àñòî óäîáíåé ïîëüçîâàòüñÿ êîìïëåêñíîé ôîð-
ìîé ðÿäà Ôóðüå, êîòîðàÿ ìîæåò áûòü ïîëó÷åíà èç (5.3) ñ ïîìîùüþ
ôîðìóë Ýéëåðà:
(
)
(
)
(
)
cos2;sin.
2
jkjkjkjk
kk
j
eeee
a-aa-a
a=a=
+-
(5.5)
Ïîäñòàâèâ (5.5) â óðàâíåíèå (5.3), ïîñëå íåñëîæíûõ ïðåîáðà-
çîâàíèé ïîëó÷èì êîìïëåêñíóþ ôîðìó ðÿäà Ôóðüå:
( )
1
,
2
jk
k
k
fAe
¥
a
=-¥
a=
å
(5.6)
ãäå A
k
% êîìïëåêñíàÿ àìïëèòóäà k-é ãàðìîíèêè:
,
k
j
kkk
k
AajbAe
-j
=-=
(5.7)
ãäå
22
k
kk
Aab
=+ $ àìïëèòóäà;
(
)
arctg
k
kk
ba
j=
$ íà÷àëüíàÿ ôàçà
k-é ãàðìîíèêè. Ïîäñòàâèâ çíà÷åíèÿ a
k
è b
k
èç (5.4) â (5.7), ïîëó÷èì:
( )
( )
2
0
1
,.
0;1;2;
jk
k
Afed
k
p
-a
=aa
=±±
p
ò
K
(5.8)
Ñîâîêóïíîñòü àìïëèòóä 0,5À
k
= 0,5À
$k
â ðàçëîæåíèè (5.6), îò-
ëîæåííûõ ïðîòèâ ñîîòâåòñòâóþùèõ ïîëîæèòåëüíûõ è îòðèöàòåëüíûõ
÷àñòîò
*
, îáðàçóåò ñèììåòðè÷íûé îòíîñèòåëüíî îñè êîîðäèíàò (âñëåä-
ñòâèå ÷åòíîñòè êîýôôèöèåíòîâ à
k
) ëèíåé÷àòûé àìïëèòóäíûé ñïåêòð.
Ñîâîêóïíîñòü îðäèíàò j
k
= $j
$k
èç (5.7), âõîäÿùèõ â ðàçëîæå-
íèå (5.6) è îòëîæåííûõ ïðîòèâ ñîîòâåòñòâóþùèõ ïîëîæèòåëüíûõ è
îòðèöàòåëüíûõ ÷àñòîò, îáðàçóåò ñèììåòðè÷íûé îòíîñèòåëüíî íà÷à-
ëà îñè êîîðäèíàò (âñëåäñòâèå íå÷åòíîñòè êîýôôèöèåíòîâ b
k
) ëè-
íåé÷àòûé ôàçîâûé ñïåêòð.
Ðàçëîæåíèå (5.3) ìîæíî ïðåäñòàâèòü è â äðóãîé ôîðìå. Åñëè
ó÷åñòü, ÷òî à
k
= À
k
cosj
k
è b
k
= À
k
sinj
k
, òî ïîñëå ïîäñòàíîâêè â
(5.3) ïîëó÷èì:
( )
( )
0
1
cos.
2
k
k
k
a
fA
k
¥
=
a=+
a-j
å
(5.9)
Åñëè ðàññìàòðèâàòü ïîñòîÿííóþ ñîñòàâëÿþùóþ a
0
/2 êàê íóëå-
âóþ ãàðìîíèêó ñ íà÷àëüíîé ôàçîé j
0
= 0, òî ðàçëîæåíèå (5.9)
ïðèìåò âèä
( )
( )
0
cos.
k
k
k
fA
k
¥
=
a=
a-j
å
(5.10)
 ÷àñòíîì ñëó÷àå, êîãäà ôóíêöèÿ f(a) ñèììåòðè÷íà îòíîñè-
òåëüíî îñè îðäèíàò (ðèñ. 5.1, à), â ðàçëîæåíèè (5.3) îêàæóòñÿ
òîëüêî ÷åòíûå (êîñèíóñîèäàëüíûå) ãàðìîíèêè:
*
Ïîíÿòèå îòðèöàòåëüíîé ÷àñòîòû íå èìååò ôèçè÷åñêîãî ñìûñëà, îäíàêî îíî óäîáíî â
òåîðåòè÷åñêèõ èññëåäîâàíèÿõ, ïîýòîìó øèðîêî èñïîëüçóåòñÿ â ñïåöèàëüíîé ëèòåðàòóðå.

147
( )
0
1
cos,
2
k
k
a
fak
¥
=
a=+a
å
(5.11)
à ïðè ñèììåòðè÷íîñòè f(a) îòíîñèòåëüíî íà÷àëà êîîðäèíàò
(ðèñ. 5.1, á) íå÷åòíûå ãàðìîíèêè
( )
1
sin.
k
k
fbk
¥
=
a=a
å
(5.12)
Ïðè ñäâèãå íà÷àëà îòñ÷åòà ôóíêöèè f(a) åå àìïëèòóäíûé
ñïåêòð íå èçìåíÿåòñÿ, à ìåíÿåòñÿ òîëüêî ôàçîâûé ñïåêòð. Äåéñòâè-
òåëüíî, ñäâèíåì ôóíêöèþ f (a) ïî îñè âðåìåíè âëåâî íà t
0
è îáî-
çíà÷èì a
1
= w
1
(t + t
0
).
Òîãäà ðàçëîæåíèå (5.9) ïðèìåò âèä
( )
( ) ( )
00
1
1
11
0
coscos
22
ãäå .
kk
kk
kk
kk
aa
fAA
kk
t
¥¥
==
ü
¢
=+=+
ï
a-ja-j
a
ý
ï
¢
j=j+w
þ
åå
(5.13)
Ïðèìåð. Ðàçëîæèòü â ðÿä Ôóðüå ïðÿìîóãîëüíûå êîëåáàíèÿ (ðèñ. 5.1, á).
Ó÷èòûâàÿ, ÷òî f (a) ñèììåòðè÷íà îòíîñèòåëüíî íà÷àëà êîîðäèíàò â ðàçëîæå-
íèè (5.3) îñòàíóòñÿ òîëüêî ñèíóñîèäàëüíûå ãàðìîíèêè (5.12), ãäå b
k
îïðåäå-
ëèòñÿ ñîãëàñíî (5.4):
( )
0
24
sin,
ãäå1,3,5,
k
bfkdk
k
p
=aa==
a
pp
ò
K
Ïîäñòàâèâ b
k
â (5.12), ïîëó÷èì ðàçëîæåíèå â ðÿä Ôóðüå:
( )
4
sinsin3sin5
.
135
f
aaa
æö
a=
+++
ç÷
p
èø
K
(5.14)
Äàëåå ñäâèíåì f (a) íà p/2 âëåâî (ñì. ðèñ. 5.1, à). Òîãäà ñîãëàñíî (5.13)
ïîëó÷èì
( )
(
)
(
)
(
)
4
sinsin3sin5
222
135
4
coscos3cos5
,
135
f
a+pa+pa+p
éù
a==
+++
êú
p
ëû
aaa
æö
=
-+-
ç÷
p
èø
K
K
(5.15)
ò. å. ïîëó÷èëè ðàçëîæåíèå ïî êîñèíóñîèäàëüíûì ñîñòàâëÿþùèì êàê è äîëæíî
áûòü äëÿ ñèììåòðè÷íîãî îòíîñèòåëüíî îñè îðäèíàò ñèãíàëà.
a
f
(
)
a
1
-
2
p
/
0
-3
2
p
/
p
/
2
3p
/
2
a
)
a
f
(
)
a
1
0
-2
p
á
)
-1
-
p
p
2
p
-1
Ðèñ. 5.1
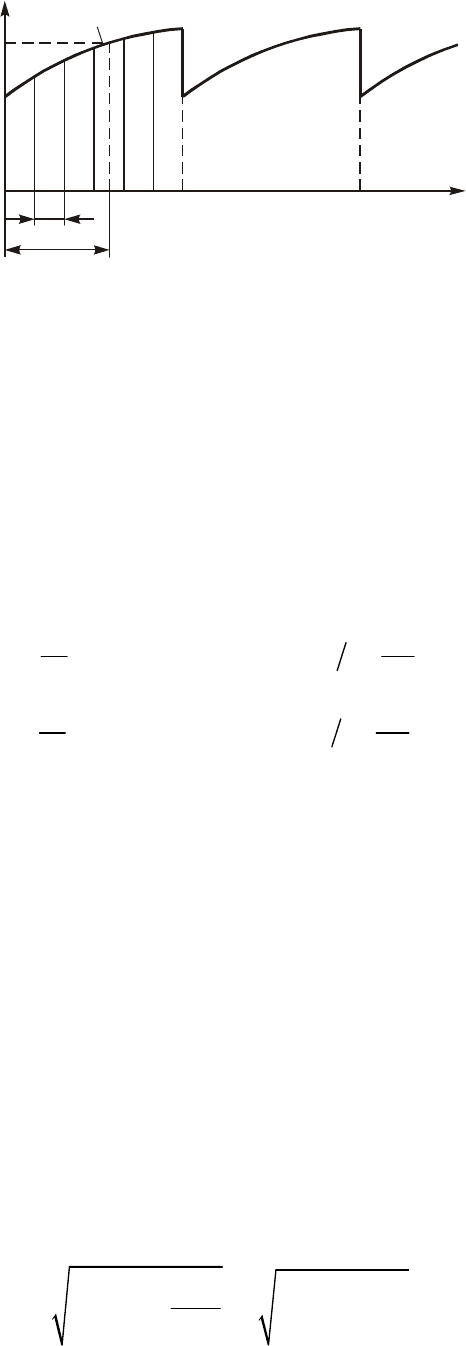
148
 ðÿäå ñëó÷àåâ, êîãäà ïåðèîäè÷íàÿ ôóíêöèÿ f (a) çàäàíà ãðà-
ôè÷åñêè è èìååò ñëîæíóþ ôîðìó, åå ðàçëîæåíèå â ðÿä Ôóðüå
ìîæíî îñóùåñòâèòü ãðàôî-àíàëèòè÷åñêèì ñïîñîáîì. Åãî ñóòü çà-
êëþ÷àåòñÿ â òîì, ÷òî ïåðèîä ñèãíàëà Ò (ðèñ. 5.2) ðàçáèâàþò íà m
èíòåðâàëîâ, ðàâíûõ Da = 2p/ò, ïðè÷åì òî÷êè ðàçðûâà f(a) íå
äîëæíû ïîïàäàòü íà ñåðåäèíó ó÷àñòêîâ ðàçáèåíèÿ; îïðåäåëÿþò
çíà÷åíèå ñèãíàëà f(a
n
) â ñåðåäèíå êàæäîãî ó÷àñòêà ðàçáèåíèÿ.
Íàõîäÿò êîýôôèöèåíòû ðàçëîæåíèÿ à
k
è b
k
ïóòåì çàìåíû èí-
òåãðàëà â (5.2) êîíå÷íîé ñóììîé
( )
( )
( )
( )
1
1
22
cos,
12
22
sin.
12
m
k
n
n
m
k
n
n
afk
n
mm
bfk
n
mm
=
=
ü
p
»
-
a
ï
ï
ý
p
ï
»
-
a
ï
þ
å
å
(5.16)
Óðàâíåíèå (5.16) ëåãêî ïðîãðàììèðóåòñÿ è ïðè âû÷èñëåíèè à
k
è b
k
, ìîæåò èñïîëüçîâàòüñÿ ÝÂÌ.
5.2. Äåéñòâóþùåå, ñðåäíåå çíà÷åíèå è ìîùíîñòü
ïåðèîäè÷åñêîãî íåãàðìîíè÷åñêîãî ñèãíàëà
Äëÿ îïðåäåëåííîñòè ïîëîæèì, ÷òî f(t) èìååò ñìûñë òîêà i (t).
Òîãäà äåéñòâóþùåå çíà÷åíèå ïåðèîäè÷åñêîãî íåãàðìîíè÷åñêîãî òî-
êà îïðåäåëÿåòñÿ ñîãëàñíî (3.5), ãäå i (t) îïðåäåëÿåòñÿ óðàâíåíèåì
(5.10):
()
( ) ( )
0
1
01
coscos.
mkmk
kk
kk
iIII
kkt
t
¥¥
==
==+
a-jw-j
åå
(5.17)
Ïîäñòàâèâ ýòî çíà÷åíèå òîêà â (3.5), ïîñëå èíòåãðèðîâàíèÿ ïî-
ëó÷èì
2
222
00
11
,
2
mk
k
kk
I
IIII
¥¥
==
=+=+
åå
(5.18)
ò. å. äåéñòâóþùåå çíà÷åíèå ïåðèîäè÷åñêîãî íåãàðìîíè÷åñêîãî òîêà
I ïîëíîñòüþ îïðåäåëÿåòñÿ äåéñòâóþùèìè çíà÷åíèÿìè åãî ãàðìîíèê
I
k
è íå çàâèñèò îò èõ íà÷àëüíûõ ôàç j
k
.
a
f
(
)
a
Da
a
n
2
p
4
p
m
0
f
(
)
a
n
Ðèñ. 5.2

149
Àíàëîãè÷íûì îáðàçîì íàõîäèì äåéñòâóþùåå çíà÷åíèå ïåðèî-
äè÷åñêîãî íåñèíóñîèäàëüíîãî íàïðÿæåíèÿ:
2
222
00
11
,
2
mk
k
kk
U
UUUU
¥¥
==
=+=+
åå
(5.19)
Ñðåäíåå çíà÷åíèå òîêà îïðåäåëÿåòñÿ ñîãëàñíî îáùåìó âûðà-
æåíèþ (3.9). Ïðè÷åì îáû÷íî áåðóò ñðåäíåå çíà÷åíèå i(t) ïî àá-
ñîëþòíîé âåëè÷èíå
( )
()
ñð
2
0
1
.
T
Idt
i
t
T
=
ò
(5.20)
Àíàëîãè÷íî îïðåäåëÿåòñÿ U
ñð(2)
.
Ñ òî÷êè çðåíèÿ òåîðèè öåïåé, áîëüøîé èíòåðåñ ïðåäñòàâëÿåò
ñðåäíÿÿ àêòèâíàÿ ìîùíîñòü íåãàðìîíè÷åñêîãî ñèãíàëà è ðàñïðå-
äåëåíèå åå ìåæäó îòäåëüíûìè ãàðìîíèêàìè.
Ñðåäíÿÿ àêòèâíàÿ ìîùíîñòü ïåðèîäè÷åñêîãî íåñèíóñîèäàëüíîãî
ñèãíàëà
()()
0
1
,
T
Puidt
tt
T
=
ò
(5.21)
ãäå
()
( )
()
( )
1
0
1
0
cos,
cos,
k
mk
k
kk
mk
k
kt
iI
t
kt
uU
t
¥
=
¥
=
ü
w-j
=
ï
ï
ý
ï
w-j+y
=
ï
þ
å
å
(5.22)
y
k
% ôàçîâûé ñäâèã ìåæäó òîêîì è íàïðÿæåíèåì k-é ãàðìîíèêè.
Ïîäñòàâëÿÿ çíà÷åíèÿ i(t) è u(t) èç (5.22) â óðàâíåíèå (5.21), ïî-
ñëå èíòåãðèðîâàíèÿ ïîëó÷àåì:
00
cos,
kkkk
kk
PUIP
¥¥
==
=y=
åå
(5.23)
ò, å. ñðåäíÿÿ çà ïåðèîä àêòèâíàÿ ìîùíîñòü ïåðèîäè÷åñêîãî íåãàð-
ìîíè÷åñêîãî ñèãíàëà ðàâíà ñóììå ìîùíîñòåé îòäåëüíûõ ãàðìîíèê.
Ôîðìóëà (5.23) ÿâëÿåòñÿ îäíîé èç ôîðì øèðîêî èçâåñòíîãî ðàâåí-
ñòâà Ïàðñåâàëÿ.
Àíàëîãè÷íî íàõîäèì ðåàêòèâíóþ ìîùíîñòü
00
sin
kkkk
kk
QUIQ
¥¥
==
=y=
åå
(5.24)
è ïîëíóþ ìîùíîñòü
22
00
.
kk
kk
SUIUI
¥¥
==
==
åå
(5.25)

150
Ñëåäóåò ïîä÷åðêíóòü, ÷òî â îòëè÷èå îò ãàðìîíè÷åñêèõ ñèãíàëîâ
(ñì. (3.121)) äëÿ íåãàðìîíè÷åñêèõ ñèãíàëîâ
22
.
SPQ
¹+ (5.26)
Âåëè÷èíà P
ècê
=
(
)
2
22
S
PQ
-
+
íîñèò íàçâàíèå ìîùíîñòè
èñêàæåíèé è õàðàêòåðèçóåò ñòåïåíü ðàçëè÷èÿ â ôîðìàõ òîêà i(t) è
íàïðÿæåíèÿ u(t).
Êðîìå ìîùíîñòè èñêàæåíèé ïåðèîäè÷åñêèå íåãàðìîíè÷åñêèå
ñèãíàëû õàðàêòåðèçóþòñÿ åùå ðÿäîì êîýôôèöèåíòîâ: ìîùíîñòè,
k
ì
= P/S; ôîðìû K
ô
= U/U
ñð (2)
; àìïëèòóäû K
a
= U
m
/U; èñêà-
æåíèé k
è
= U
1
/U; ãàðìîíèê k
ã
=
2
1
2
k
k
UU
¥
=
å
è äð. Äëÿ ñèíóñîè-
äàëüíîãî ñèãíàëà k
ô
= p/2
2
» 1,11; k
a
=
2
» 1,41; k
è
= 1; k
ã
= 0.
5.3. Ñïåêòðû ïåðèîäè÷åñêèõ íåãàðìîíè÷åñêèõ ñèãíàëîâ
Ðàññìîòðèì ïîñëåäîâàòåëüíîñòü ïðÿìîóãîëüíûõ èìïóëüñîâ,
èçîáðàæåííóþ íà ðèñ. 5.3, à. Ñèãíàëû ïîäîáíîé ôîðìû íàõîäÿò
î÷åíü øèðîêîå ïðèìåíåíèå â ðàäèîòåõíèêå è ýëåêòðîñâÿçè: òåëå-
ãðàôèÿ, öèôðîâûå ñèñòåìû ïåðåäà÷è, ñèñòåìû ìíîãîêàíàëüíîé ñâÿ-
çè ñ âðåìåííûì ðàçäåëåíèåì êàíàëîâ, ðàçëè÷íûå èìïóëüñíûå è
öèôðîâûå óñòðîéñòâà è äð. (ñì. ãë. 19). Èìïóëüñíàÿ ïîñëåäîâà-
òåëüíîñòü õàðàêòåðèçóåòñÿ ñëåäóþùèìè îñíîâíûìè ïàðàìåòðàìè:
àìïëèòóäîé èìïóëüñà A
è
*
, åãî äëèòåëüíîñòüþ t
è
è ïåðèîäîì ñëå-
äîâàíèÿ Ò. Îòíîøåíèå ïåðèîäà Ò ê äëèòåëüíîñòè t
è
íàçûâàåòñÿ
ñêâàæíîñòüþ èìïóëüñîâ è îáîçíà÷àåòñÿ ÷åðåç q = T/t
è
. Îáû÷íî
çíà÷åíèÿ ñêâàæíîñòè èìïóëüñîâ ëåæàò â ïðåäåëàõ îò íåñêîëüêèõ
åäèíèö (â èçìåðèòåëüíîé òåõíèêå, óñòðîéñòâàõ äèñêðåòíîé ïåðå-
äà÷è è îáðàáîòêè èíôîðìàöèè), äî íåñêîëüêèõ ñîòåí èëè òûñÿ÷ (â
ðàäèîëîêàöèè).
Äëÿ íàõîæäåíèÿ ñïåêòðà ïîñëåäîâàòåëüíîñòè ïðÿìîóãîëüíûõ
èìïóëüñîâ âîñïîëüçóåìñÿ ðÿäîì Ôóðüå â êîìïëåêñíîé ôîðìå (5.6).
*
Âåëè÷èíà A
è
ìîæåò èìåòü ñìûñë êàê íàïðÿæåíèÿ, òàê è òîêà.
f
t
(
)
0
a
)
f
t
(
)
0
á
)
A
è
t
è
t
è
/2-
t
è
/2
T
t
è
T
A
è
t
t
Ðèñ. 5.3
