Бакалов В.П. Основы теории цепей. 3-е издание
Подождите немного. Документ загружается.


161
(
)
21
ñâ
123
.
pt
m
m
xe
AAtAtAt
-
=
++++
K
(6.8)
Ïðåäñòàâëÿåò ïðàêòè÷åñêèé èíòåðåñ è ñëó÷àé, êîãäà êîðíè ïî-
ïàðíî êîìïëåêñíî-ñîïðÿæåííûå ð
k,k$1
= %a ± jw
ñ
. Ïðè ýòîì â
ôîðìóëå (6.7) ñîîòâåòñòâóþùàÿ ïàðà êîðíåé ð
k,k$1
çàìåíÿåòñÿ ñëà-
ãàåìûìè âèäà
(
)
sin,
t
c
Ae
t
-a
w+q
(6.9)
ãäå A, q % ïîñòîÿííûå èíòåãðèðîâàíèÿ, îïðåäåëÿåìûå òàêæå èç
íà÷àëüíûõ óñëîâèé.
6.3. Ïåðåõîäíûå ïðîöåññû â öåïÿõ ïåðâîãî ïîðÿäêà
Ðàññìîòðèì ïðèìåíåíèå êëàññè÷åñêîãî ìåòîäà ê ðàñ÷åòó ïåðå-
õîäíûõ ïðîöåññîâ â öåïÿõ ïåðâîãî ïîðÿäêà. Ýòî öåïè, ñîäåðæàùèå
òîëüêî îäíîòèïíûå ðåàêòèâíûå ýëåìåíòû (åìêîñòè èëè èíäóê-
òèâíîñòè), ïðîöåññû, â êîòîðûõ îïèñûâàþòñÿ äèôôåðåíöèàëüíûìè
óðàâíåíèÿìè ïåðâîãî ïîðÿäêà
()
10
dx
bbxw
t
dt
+= . (6.10)
Ïðèìåðîì öåïåé ïåðâîãî ïîðÿäêà ÿâëÿþòñÿ ïðîñòåéøèå RL è
RC öåïè.
Ïåðåõîäíûå ïðîöåññû â RL-öåïÿõ. Ðàññìîòðèì âêëþ÷åíèå RL-
öåïè ê èñòî÷íèêó íàïðÿæåíèÿ u(t) (ðèñ. 6.1). Èç ðèñ. 6.1 ñëåäóåò,
÷òî äî êîììóòàöèè êëþ÷ Ê ðàçîìêíóò, ïîýòîìó òîê i
L
(0
$
) = 0 è
öåïü íàõîäèòñÿ ïðè íóëåâûõ íà÷àëüíûõ óñëîâèÿõ.  ìîìåíò t = 0
êëþ÷îì Ê çàìûêàåì (îñóùåñòâèì êîììóòàöèþ) öåïü, ïîäêëþ÷èâ åå
ê èñòî÷íèêó íàïðÿæåíèÿ u(t). Ïîñëå çàìûêàíèÿ êëþ÷à Ê â öåïè
íà÷íåòñÿ ïåðåõîäíûé ïðîöåññ. Äëÿ åãî ìàòåìàòè÷åñêîãî îïèñàíèÿ
âûáåðåì â êà÷åñòâå íåçàâèñèìîé ïåðåìåííîé i
L
= i è ñîñòàâèì îò-
íîñèòåëüíî íåå äèôôåðåíöèàëüíîå óðàâíåíèå ïî ÇÍÊ:
( )
L
di
RiuRiLu
t
dt
+=+=. (6.11)
Óðàâíåíèå (6.11) îòíîñèòñÿ ê ëèíåéíûì íåîäíîðîäíûì äèôôå-
ðåíöèàëüíûì óðàâíåíèÿì ïåðâîãî ïîðÿäêà òèïà (6.3), ðåøåíèå êî-
òîðîãî ìîæíî çàïèñàòü ñîãëàñíî (6.5) â ôîðìå
ïðñâ
iii
=+
, (6.12)
ãäå i
ñâ
% ñâîáîäíàÿ ñîñòàâëÿþùàÿ òîêà,
îáóñëîâëåííàÿ ñâîáîäíûìè ïðîöåññàìè,
ïðîòåêàþùèìè â öåïè áåç ó÷àñòèÿ èñòî÷-
íèêà u(t); i
np
% ïðèíóæäåííàÿ ñîñòàâ-
ëÿþùàÿ òîêà, îáóñëîâëåííàÿ äåéñòâèåì èñ-
òî÷íèêà íàïðÿæåíèÿ u(t).
R
u
L
L
ut
()
K
Ðèñ. 6.1

162
Ñâîáîäíàÿ ñîñòàâëÿþùàÿ òîêà i
ñâ
åñòü îáùåå ðåøåíèå îäíî-
ðîäíîãî äèôôåðåíöèàëüíîãî óðàâíåíèÿ
ñâ
ñâ
0
di
RiL
dt
+=
(6.13)
è ñîãëàñíî (6.7)
ñâ
,
pt
iAe
=
(6.14)
ãäå À % ïîñòîÿííàÿ èíòåãðèðîâàíèÿ; ð % êîðåíü õàðàêòåðèñòè÷å-
ñêîãî óðàâíåíèÿ òèïà (6.6);
0.
pLR
+=
(6.15)
Îòñþäà p = %R/L. Âåëè÷èíà 1/|ð| íîñèò íàçâàíèå ïîñòîÿííîé
âðåìåíè öåïè. Â íåðàçâåòâëåííîé RL-öåïè t = L/R.
Ïðèíóæäåííàÿ ñîñòàâëÿþùàÿ i
ïp
ìîæåò áûòü îïðåäåëåíà êàê
÷àñòíîå ðåøåíèå óðàâíåíèÿ (6.11). Îäíàêî, êàê áûëî óêàçàíî âû-
øå, i
ïp
ìîæíî íàéòè áîëåå ïðîñòî ìåòîäàìè ðàñ÷åòà óñòàíîâèâøå-
ãîñÿ ðåæèìà öåïè. Ðàññìîòðèì äâà ÷àñòíûõ ñëó÷àÿ:
(
)
(
)
(
)
1)const;2)sin.
m
u
uUuU
t
tt
===
w+j
 ïåðâîì ñëó÷àå ïðèíóæäåííàÿ ñîñòàâëÿþùàÿ ìîæåò áûòü îï-
ðåäåëåíà èç óñòàíîâèâøåãîñÿ ðåæèìà: i
ïp
= U/R. Äëÿ íàõîæäåíèÿ
ïîñòîÿííîé èíòåãðèðîâàíèÿ A ïåðåïèøåì (6.12) â ôîðìå i = Àå
t/
t
+
+ U/R è ó÷òåì íà÷àëüíûå óñëîâèÿ äëÿ i, à òàêæå ïåðâûé çàêîí
êîììóòàöèè (6.1):
(
)
(
)
0
00
iiAUR
-+
===+
.
Îòñþäà À = %U/R. Òàêèì îáðàçîì, çàêîí èçìåíåíèÿ òîêà â RL-
öåïè îïðåäåëÿåòñÿ óðàâíåíèåì
( )
.
1
t
U
i
e
R
-t
=
-
(6.16)
Íàïðÿæåíèå íà èíäóêòèâíîñòè ñîãëàñíî (1.9)
.
t
L
di
uLUe
dt
-t
== (6.17)
Íà ðèñ. 6.2 èçîáðàæåíû ãðàôèêè
çàâèñèìîñòè i(t) è u
L
(t). Àíàëèç ïî-
ëó÷åííûõ óðàâíåíèé (6.16) è (6.17)
ïîêàçûâàåò, ÷òî ÷åì áîëüøå ïîñòî-
ÿííàÿ âðåìåíè öåïè t, òåì ìåäëåí-
íåå çàòóõàåò ïåðåõîäíîé ïðîöåññ.
Íà ïðàêòèêå ïðèíÿòî ñ÷èòàòü ïåðå-
õîäíîé ïðîöåññ çàêîí÷åííûì ïðè
t = (3...5)t, ïðè t = 3t òîê äîñòèãà-
åò 95% ñâîåãî óñòàíîâèâøåãîñÿ çíà-
ui
,
u
L
()
t
t
0
U/R
U/e
U
i
()
t
i
ïð
t
-
U/R
t
ñ
â
U
i
e
R
t
=
Ðèñ. 6.2

163
÷åíèÿ, à ïðè t = 5t % áîëåå 99%. Ãðàôè÷åñêè ïîñòîÿííàÿ âðåìåíè
t ìîæåò îïðåäåëèòüñÿ êàê èíòåðâàë âðåìåíè íà îñè t îò t = 0 äî
òî÷êè ïåðåñå÷åíèÿ êàñàòåëüíîé ê u
L
(ðèñ. 6.2), â óêàçàííûé ìîìåíò
íàïðÿæåíèå íà u
L
óìåíüøàåòñÿ â å ðàç ïî ñðàâíåíèþ ñ íà÷àëüíûì.
Àíàëèç ïîëó÷åííûõ ðåçóëüòàòîâ ïîêàçûâàåò, ÷òî ïðè íóëåâûõ
íà÷àëüíûõ óñëîâèÿõ â ìîìåíò t = 0
+
èíäóêòèâíîñòü âåäåò ñåáÿ êàê
áåñêîíå÷íî áîëüøîå ñîïðîòèâëåíèå (ðàçðûâ öåïè), à ïðè t = ¥ êàê
áåñêîíå÷íî ìàëîå ñîïðîòèâëåíèå (êîðîòêîå çàìûêàíèå öåïè).
Äëÿ âòîðîãî ñëó÷àÿ ïðèíóæäåííàÿ ñîñòàâëÿþùàÿ òîêà ñîãëàñ-
íî § 3.6
(
)
ïð
sin,
m
u
iI
t
=
w+j-j
ãäå
22
()
mm
IU
RL
=
+w
, j =
= arctg(wL/R). Ïîñòîÿííàÿ èíòåãðèðîâàíèÿ îïðåäåëÿåòñÿ èç óðàâ-
íåíèÿ
(
)
(
)
(
)
0sin,
00
LLm
u
iiAI
-+
===+
j-j
îòêóäà
(
)
sin
m
u
AI
=-
j-j
. Ñëåäîâàòåëüíî, çàêîí èçìåíåíèÿ òîêà
â öåïè â ýòîì ñëó÷àå áóäåò
(
)
(
)
sinsin.
t
mm
uu
iIIe
t
-t
=-
w+j-jj-j
(6.18)
Íà ðèñ. 6.3 èçîáðàæåíà âðåìåííàÿ çàâèñèìîñòü òîêà (6.18). Íà-
ïðÿæåíèå íà èíäóêòèâíîñòè
( )
( )
sin
2
sin,
LmL
u
t
mL
u
di
uLU
t
dt
R
Ue
L
-t
==+
w+j-j+p
+
j-j
w
(6.19)
ãäå U
mL
= wLI
m
.
Àíàëèç óðàâíåíèÿ (6.18) ïîêàçûâàåò, ÷òî â ñëó÷àå ïîäêëþ÷åíèÿ
öåïè ê èñòî÷íèêó u(t) â ìîìåíò, êîãäà j
u
= j ± p/2 â ïîñëåäíåé
ìîãóò âîçíèêàòü ñâåðõòîêè. Åñëè ïîñòîÿííàÿ âðåìåíè öåïè t äîñòà-
òî÷íî âåëèêà, òî ñêà÷îê òîêà â íà÷àëüíûé ïåðèîä ìîæåò äîñòèãàòü
i
max
» 2I
m
. Íàïðîòèâ, ïðè âêëþ÷åíèè öåïè â ìîìåíò, êîãäà j
u
= j,
â íåé ñðàçó íàñòóïàåò óñòàíîâèâøèéñÿ ðåæèì. Àíàëîãè÷íàÿ êàðòè-
íà íàáëþäàåòñÿ è ñ íàïðÿæåíèåì íà èíäóêòèâíîñòè (6.19).
 êà÷åñòâå âòîðîãî ïðèìåðà ðàñ÷åòà ðàññìîòðèì ñëó÷àé íåíó-
ëåâûõ íà÷àëüíûõ óñëîâèé â RL-öåïè (ðèñ. 6.4). Ê ìîìåíòó êîì-
ìóòàöèè â äàííîé öåïè áûëà çàïàñåíà ýíåðãèÿ ìàãíèòíîãî ïîëÿ,
ðàâíàÿ W
L
= Li
2
(0
$
)/2, ãäå i(0
$
) = U/(R
0
+ R). Ïîñëå êîììóòà-
öèè â RL-öåïè âîçíèêàåò ïåðåõîäíûé ïðîöåññ, îïèñûâàåìûé
óðàâíåíèåì:
0,
di
LRi
dt
+=
(6.20)
ò. å. i
ïp
= 0. Ðåøàÿ óðàâíåíèå (6.20), íàõîäèì ñ ó÷åòîì (6.13) $
(6.15):
ñâ
.
ptt
iiAeAe
-t
===
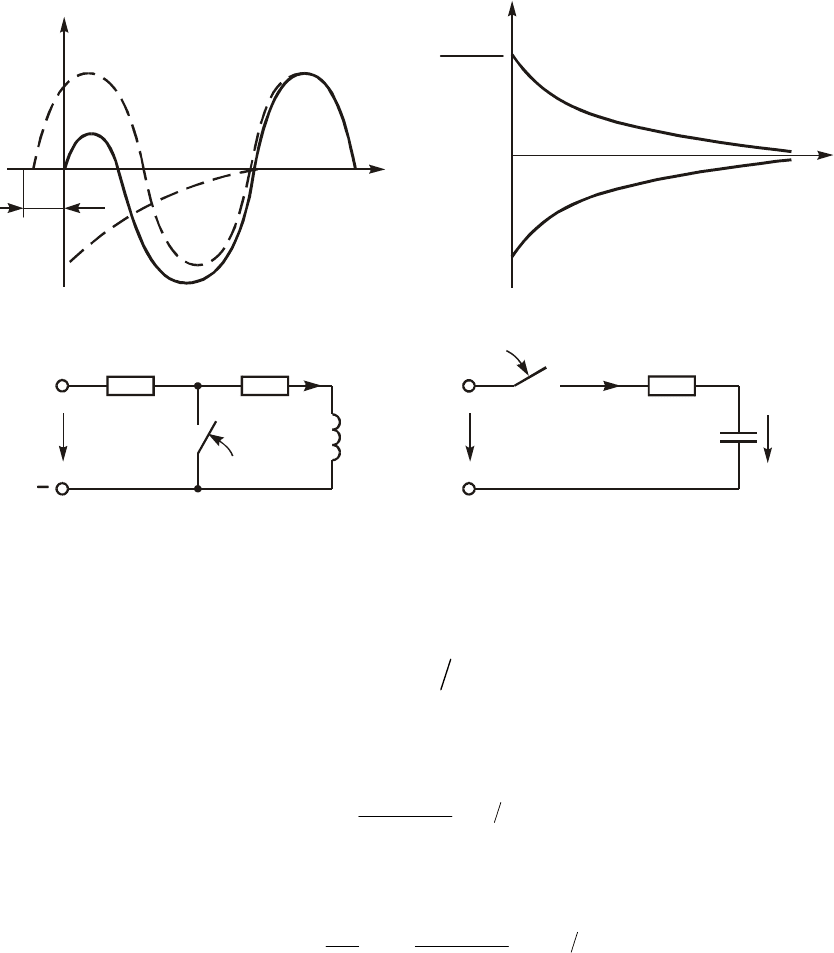
164
Ïîñòîÿííóþ À íàõîäèì èç íà÷àëüíîãî óñëîâèÿ i(0
$
) è çàêîíà êîì-
ìóòàöèè (6.1):
(
)
(
)
(
)
0
.
00
iiUA
RR
-+
===
+
Îêîí÷àòåëüíî çàêîí èçìåíåíèÿ òîêà â ïåðåõîäíîì ðåæèìå îïèñû-
âàåòñÿ óðàâíåíèåì
0
.
t
U
ie
RR
-t
=
+
(6.21)
Íàïðÿæåíèå u
L
îïðåäåëÿåòñÿ êàê
0
Re.
t
L
diU
uL
dtRR
-t
==-
+
(6.22)
Íà ðèñ. 6.5 èçîáðàæåíû ãðàôèêè i è u
L
. Ñëåäóåò îòìåòèòü, ÷òî
âñÿ ýíåðãèÿ W
L
, çàïàñåííàÿ â èíäóêòèâíîñòè ñ òå÷åíèåì âðåìåíè,
ðàñõîäóåòñÿ íà òåïëîâûå ïîòåðè â R. Ïðè íåíóëåâûõ íà÷àëüíûõ
óñëîâèÿõ L âåäåò ñåáÿ êàê èñòî÷íèê òîêà.
Ïåðåõîäíûå ïðîöåññû â RÑ-öåïÿõ. Ïðè ðàñ÷åòå ïåðåõîäíûõ
ïðîöåññîâ â RÑ-öåïÿõ â êà÷åñòâå íåçàâèñèìîé ïåðåìåííîé âûáèðàþò
u
C
. Çàòåì òàêæå ñîñòàâëÿþò äèôôåðåíöèàëüíîå óðàâíåíèå äëÿ çà-
äàííîé RÑ-öåïè, ðåøåíèå êîòîðîãî ñ ó÷åòîì íà÷àëüíûõ óñëîâèé äëÿ
u
C
(0) è îïðåäåëÿåò çàêîí èçìåíåíèÿ íàïðÿæåíèÿ íà åìêîñòè.
Ðàññìîòðèì âíà÷àëå RC-öåïü ïðè íóëåâûõ íà÷àëüíûõ óñëîâèÿõ
(ðèñ. 6.6), êîòîðàÿ ïîäêëþ÷àåòñÿ â ìîìåíò t = 0 ê èñòî÷íèêó ïî-
ñòîÿííîãî è(t) = U èëè ñèíóñîèäàëüíîãî è(t) = U
m
sin(wt + j
u
)
íàïðÿæåíèÿ. Ïåðåõîäíûé ïðîöåññ â äàííîé öåïè îïèñûâàåòñÿ äèô-
ôåðåíöèàëüíûì óðàâíåíèåì
j
i
/
w
t
i
i
ñâ
0
i
ïð
i
t
u
L
()
t
i
()
t
u
L
(0)
+
R
+
R
0
U
ui
,
0
Ðèñ. 6.3 Ðèñ. 6.5
L
U
K
R
i
+
R
0
u
C
C
R
i
K
u
()
t
Ðèñ. 6.4 Ðèñ. 6.6

165
,
C
CC
du
uRiRCuu
dt
+=+=
(6.23)
ðåøåíèå êîòîðîãî èùåì òàêæå â ôîðìå ñóììû îáùåãî è ÷àñòíîãî
ðåøåíèé, îïðåäåëÿþùèõ ñâîáîäíóþ è ïðèíóæäåííóþ ñîñòàâëÿþùèå:
ñâ ïð
.
CCC
uuu
=+
(6.24)
Ñâîáîäíàÿ ñîñòàâëÿþùàÿ ÿâëÿåòñÿ ðåøåíèåì îäíîðîäíîãî äèô-
ôåðåíöèàëüíîãî óðàâíåíèÿ
ñâ
ñâ
0;
C
C
du
RCu
dt
+=
(6.25)
ñâ
,
pt
C
uAe
=
(6.26)
ãäå ð îïðåäåëÿåòñÿ èç õàðàêòåðèñòè÷åñêîãî óðàâíåíèÿ
10;1.
RCppRC
+==-
Âåëè÷èíà RC íîñèò íàçâàíèå ïîñòîÿííîé âðåìåíè RC-öåïè è
îáîçíà÷àåòñÿ ÷åðåç t.
Îïðåäåëèì ïðèíóæäåííóþ ñîñòàâëÿþùóþ u
Cïp
äëÿ ñëó÷àÿ, êî-
ãäà u(t) = U = const. Èç ðèñ. 6.6 ñëåäóåò, ÷òî â óñòàíîâèâøåìñÿ
ðåæèìå u
Cïp
= U. Ñëåäîâàòåëüíî, ñ ó÷åòîì (6.24) è (6.26) óðàâíå-
íèå äëÿ è
C
ïðèìåò âèä è
C
= Ae
$
t/
t
+ U. Äëÿ íàõîæäåíèÿ ïîñòîÿí-
íîé èíòåãðèðîâàíèÿ À ó÷òåì íóëåâûå íà÷àëüíûå óñëîâèÿ äëÿ u
C
(0
$
)
è âòîðîé çàêîí êîììóòàöèè (6.2): u
C
(0
$
) = u
C
(0
+
) = 0 = A + U,
îòêóäà À = %U. Òàêèì îáðàçîì, ïîëó÷àåì îêîí÷àòåëüíî:
(
)
.
1
t
C
uU
e
-t
=
-
(6.27)
Òîê â öåïè îïðåäåëÿåòñÿ ñîãëàñíî (1.12):
.
C
t
duU
iCe
dtR
-t
== (6.28)
Íà ðèñ. 6.7 èçîáðàæåíû ãðàôè÷åñêèå çàâèñèìîñòè u
Ñ
(t) è i(t).
Àíàëèç ïîëó÷åííûõ ðåçóëüòàòîâ ïîêàçûâàåò, ÷òî â ìîìåíò
t = 0
+
åìêîñòü Ñ (ïðè íóëåâûõ íà÷àëüíûõ óñëîâèÿõ) âåäåò ñåáÿ
u
Ñ
ïð
t
u
C
()
t
i
()
t
-
U
0
u
Ñ
ñâ
UR
/
u
i
u
Ñ
()
t
j
C
/
w
t
u
Ñ
()
t
u
Ñ
ñâ
Ðèñ. 6.7 Ðèñ. 6.8

166
êàê êîðîòêîçàìêíóòûé ó÷àñòîê. Íàïðîòèâ, ïðè t = ¥ åìêîñòü ïðåä-
ñòàâëÿåò ñîáîé áåñêîíå÷íî áîëüøîå ñîïðîòèâëåíèå (ðàçðûâ öåïè
äëÿ ïîñòîÿííîãî òîêà).
Ðàññìîòðèì ñëó÷àé ãàðìîíè÷åñêîãî âîçäåéñòâèÿ. Íåòðóäíî âè-
äåòü ÷òî ïðè ýòîì
(
)
ïð
sin,
2
CmC
u
uU
t
=
w+j+j-p
(6.29)
ãäå
( )
( )
[ ]
2
2
1
,
1
arctg,
1
m
mCCmC
U
UXI
C
R
C
RC
ü
==
ï
w
ý
+
w
ï
j=
w
þ
(6.30)
à íàïðÿæåíèå
(
)
sin.
2
t
CmC
u
uAeU
t
-t
=+
w+j+j-p
Ïîñòîÿííàÿ À íàõîäèòñÿ èç íà÷àëüíûõ óñëîâèé äëÿ u
C
(0
+
) ïðè
t = 0
+
:
(
)
sin.
2
mC
u
AU
=-
j+j-p
Îêîí÷àòåëüíî çàêîí èçìåíåíèÿ íàïðÿæåíèÿ
(
)
( )
sin
2
sin.
2
CmC
u
t
mC
u
uU
t
Ue
-t
=-
w+j+j-p
-
j+j-p
(6.31)
Íà ðèñ. 6.8 èçîáðàæåí ãðàôèê çàâèñèìîñòè u
C
(t). Àíàëèç óðàâ-
íåíèÿ (6.31) ïîêàçûâàåò, ÷òî â ñëó÷àå íåóäà÷íîãî âêëþ÷åíèÿ ïðè
j
u
= p $ j è áîëüøîé t â öåïè ìîãóò âîçíèêàòü ïåðåíàïðÿæåíèÿ,
äîñòèãàþùèå íà åìêîñòè âåëè÷èíû u
Cmax
» 2U
mC
.  ñëó÷àå óäà÷-
íîãî âêëþ÷åíèÿ, êîãäà j
u
= p/2 $ j, â öåïè ñðàçó íàñòóïàåò óñòà-
íîâèâøèéñÿ ðåæèì.
Òîê â öåïè
( )
( )
sin
1
sin.
2
C
mC
u
t
mC
u
du
iCI
t
dt
Ie
RC
-t
==+
w+j+j
+
j+j-p
w
(6.32)
Ðàññìîòðèì òåïåðü ñëó÷àé íåíóëåâûõ íà÷àëüíûõ óñëîâèé, êîãäà
åìêîñòü Ñ, çàðÿæåííàÿ äî íàïðÿæåíèÿ U, ðàçðÿæàåòñÿ íà ñî-
ïðîòèâëåíèå R (ðèñ. 6.9). Ê ìîìåíòó êîììóòàöèè â åìêîñòè áûëà
çàïàñåíà ýíåðãèÿ W
C
= CU
2
/2. Ïîñëå êîììóòàöèè âîçíèêàåò ïåðå-
õîäíûé ïðîöåññ, îïðåäåëÿåìûé óðàâíåíèåì
0,
C
C
du
RCu
dt
+=
(6.33)
ò. å. èìååò ìåñòî ñâîáîäíûé ðåæèì ðàçðÿäà (åìêîñòè):
ñâ
.
ptt
CC
uuAeAe
-t
===
(6.34)

167
Ïîñòîÿííóþ èíòåãðèðîâàíèÿ À íàõîäèì èç íà÷àëüíîãî óñëîâèÿ
äëÿ u
C
(0
+
) = U è çàêîíà êîììóòàöèè (6.2):
(
)
(
)
.
0
0
CC
uuUA
-
===
+
Òàêèì îáðàçîì, ïîëó÷àåì çàêîí èçìåíåíèÿ íàïðÿæåíèÿ íà åì-
êîñòè
t
C
uUe
-t
=
(6.35)
è òîêà â öåïè
.
C
t
duU
iCe
dtR
-t
==- (6.36)
Çíàê «$» â óðàâíåíèè (6.36) äëÿ òîêà ñâèäåòåëüñòâóåò î òîì,
÷òî òîê ðàçðÿäà íàïðàâëåí ïðîòèâîïîëîæíî îïîðíîìó íàïðàâëåíèþ
íàïðÿæåíèÿ è
Ñ
â åìêîñòè (ñì. § 1.2). Íà ðèñ. 6.10 ïðèâåäåíû ãðà-
ôèêè èçìåíåíèÿ íàïðÿæåíèÿ è
Ñ
(t) è òîêà i(t) äàííîé RÑ-öåïè.
Ñëåäóåò ïîä÷åðêíóòü, ÷òî âñÿ çàïàñåííàÿ ýíåðãèÿ W
C
åìêîñòè ñ
òå÷åíèåì âðåìåíè ïðåîáðàçóåòñÿ â ýëåìåíòå R â òåïëî. Ïðè íåíó-
ëåâûõ íà÷àëüíûõ óñëîâèÿõ Ñ âåäåò ñåáÿ êàê èñòî÷íèê íàïðÿæåíèÿ.
6.4. Ïåðåõîäíûå ïðîöåññû â öåïÿõ âòîðîãî ïîðÿäêà
Ðàíåå ðàññìàòðèâàëèñü ïåðåõîäíûå ïðîöåññû â RL- è RÑ-öå-
ïÿõ, êîòîðûå îòíîñÿòñÿ ê öåïÿì ïåðâîãî ïîðÿäêà, òàê êàê îïèñû-
âàþòñÿ äèôôåðåíöèàëüíûìè óðàâíåíèÿìè ïåðâîãî ïîðÿäêà (6.11),
(6.23). Ïðè íàëè÷èè â öåïè äâóõ íåçàâèñèìûõ íàêîïèòåëåé
ýíåðãèè ïåðåõîäíûå ïðîöåññû â íèõ îïèñûâàþòñÿ óðàâíåíèåì
âòîðîãî ïîðÿäêà. Ïðîñòåéøèì ïðèìåðîì òàêîé öåïè ÿâëÿåòñÿ
ïîñëåäîâàòåëüíûé êîëåáàòåëüíûé
êîíòóð (ðèñ. 6.11). Äëÿ ýòîãî êîíòóðà
ìîæíî ïî àíàëîãèè ñ RL- è RÑ-
öåïüþ ñîñòàâèòü äèôôåðåíöèàëüíîå
óðàâíåíèå âòîðîãî ïîðÿäêà, âûáðàâ â
êà÷åñòâå íåçàâèñèìîé ïåðåìåííîé íà-
ïðÿæåíèå íà åìêîñòè
.
LRCC
di
uuuLRiuu
dt
++=++=
u
C
C
R
i
K
U
1
2
+
t
u
C
()
t
i
()
t
ui
,
0
U
-/
UR
Ðèñ. 6.9 Ðèñ. 6.10
u
L
C
R
i
K
U
1
2
+
u
C
L
Ðèñ. 6.11
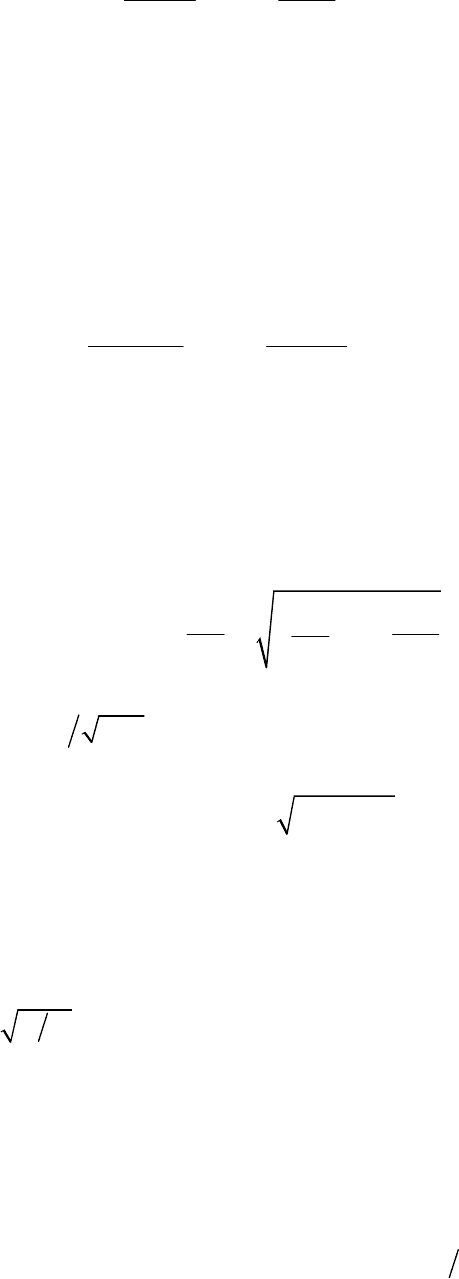
168
Ó÷èòûâàÿ, ÷òî i = Cdu
C
/dt îêîí÷àòåëüíî ïîëó÷àåì
2
2
.
CC
C
dudu
LCRCuu
dtdt
++=
(6.37)
Ðåøåíèå äèôôåðåíöèàëüíîãî óðàâíåíèÿ (6.37) èùåòñÿ ñîãëàñíî
(6.5) â ôîðìå ñóììû ñâîáîäíîé u
Cñâ
è ïðèíóæäåííîé u
Cïð
ñîñòàâ-
ëÿþùèõ:
ñâ ïð
CCC
uuu
=+
. (6.38)
Âèä u
Cïð
çàâèñèò îò õàðàêòåðà ïðèëîæåííîãî íàïðÿæåíèÿ, à
u
Cñâ
îïðåäåëèòñÿ ðåøåíèåì îäíîðîäíîãî äèôôåðåíöèàëüíîãî óðàâ-
íåíèÿ âòîðîãî ïîðÿäêà:
2
ñâ ñâ
ñâ
2
0.
CC
C
dudu
LCRCu
dtdt
++=
(6.39)
Ðåøåíèå óðàâíåíèÿ (6.39) çàâèñèò îò âèäà êîðíåé õàðàêòåðèñ-
òè÷åñêîãî óðàâíåíèÿ
2
10.
LCpRCp
++=
(6.40)
Êîðíè óðàâíåíèÿ (6.40) îïðåäåëÿþòñÿ òîëüêî ïàðàìåòðàìè öåïè
íåçàâèñèìî îò âûáðàííîé ïåðåìåííîé:
2
1,2
1
.
2
2
R
R
p
LLC
L
æö
=-±-
ç÷
èø
(6.41)
Âåëè÷èíà a = R / 2L íîñèò íàçâàíèå êîýôôèöèåíòà çàòóõàíèÿ
êîíòóðà, à
0
1
LC
w= åñòü ðåçîíàíñíàÿ ÷àñòîòà êîíòóðà (ñì.
§ 4.2). Òàêèì îáðàçîì, óðàâíåíèå (6.41) ìîæíî ïåðåïèñàòü â âèäå
2
2
1,2
0
.
p
=-a±a-w
(6.42)
Õàðàêòåð ïåðåõîäíîãî ïðîöåññà ñóùåñòâåííûì îáðàçîì çàâèñèò
îò âèäà êîðíåé ð
1
, ð
2
, êîòîðûå ìîãóò áûòü:
1) âåùåñòâåííûìè è ðàçëè÷íûìè (ïðè R > 2r);
2) êîìïëåêñíî-ñîïðÿæåííûìè (ïðè R < 2r);
3) âåùåñòâåííûìè è ðàâíûìè (ïðè R = 2r).
Çäåñü r =
LC
% õàðàêòåðèñòè÷åñêîå ñîïðîòèâëåíèå êîíòóðà
(ñì. ôîðìóëó (4.22)).
Ðàçðÿä åìêîñòè íà RL-öåïü. Äëÿ èññëåäîâàíèÿ õàðàêòåðà ïå-
ðåõîäíîãî ïðîöåññà âî âñåõ ýòèõ ñëó÷àÿõ ðàññìîòðèì ðàçðÿä åì-
êîñòè Ñ íà öåïü RL (ñì. ðèñ. 6.11). Òàê êàê äî êîììóòàöèè åì-
êîñòü Ñ áûëà çàðÿæåíà äî íàïðÿæåíèÿ U, òî èìååì íåíóëåâûå íà-
÷àëüíûå óñëîâèÿ:
(
)
(
)
2
;2.
00
CC
uUWCU
--
==
Ïîñëå êîììóòàöèè (ïåðåêëþ÷åíèå êëþ÷à Ê èç ïîëîæåíèÿ 1 â
ïîëîæåíèå 2 åìêîñòü íà÷íåò ðàçðÿæàòüñÿ è â öåïè âîçíèêíåò ñâî-
169
áîäíûé ïåðåõîäíûé ïðîöåññ. Íàéäåì çàêîí èçìåíåíèÿ òîêà è íà-
ïðÿæåíèé íà îòäåëüíûõ ýëåìåíòàõ öåïè äëÿ ñëó÷àÿ 1)%3).
 ïåðâîì ñëó÷àå, êîãäà R > 2r êîðíè p
1
è ð
2
â (6.41) áóäóò âå-
ùåñòâåííûìè è ðàçëè÷íûìè, è ðåøåíèå óðàâíåíèÿ îïðåäåëèòñÿ ñî-
ãëàñíî (6.7):
12
ñâ 12
ptpt
CC
uuAeAe
==+
, (6.43)
ãäå A
1
è A
2
% ïîñòîÿííûå èíòåãðèðîâàíèÿ. Äëÿ îïðåäåëåíèÿ A
1
è
A
2
çàïèøåì åùå óðàâíåíèå äëÿ òîêà â öåïè:
( )
12
1122
.
C
ptpt
du
iCC
pAepAe
dt
==
+
(6.44)
Ïîñòîÿííûå A
1
è A
2
ìîæíî íàéòè èç íà÷àëüíûõ óñëîâèé äëÿ
u
C
(0
$
) = U è i(0
$
) = 0 (ïðè t = 0
$
) è çàêîíîâ êîììóòàöèè (6.1),
(6.2):
}
12
1122
,
0.
AAU
pApA
+=
+=
(6.45)
Èç ðåøåíèÿ ñèñòåìû óðàâíåíèå (6.45)
(
)
(
)
1221
1212
;.
AUpAUp
pppp
=-=
--
 ðåçóëüòàòå ïîëó÷àåì óðàâíåíèÿ äëÿ íàïðÿæåíèÿ U
C
è òîêà i:
( )
21
12
12
,
ptpt
C
U
u
pepe
pp
=
-
-
(6.46)
( )
( )
21
12
.
ptpt
U
i
ee
L
pp
=
-
-
(6.47)
Çàêîí èçìåíåíèÿ íàïðÿæåíèÿ íà èíäóêòèâíîñòè îïðåäåëÿåòñÿ
ïðè ýòîì óðàâíåíèåì
( )
21
21
12
.
ptpt
L
diU
uL
pepe
dtpp
==
-
-
(6.48)
Èç óðàâíåíèé (6.46)%(6.48) ñëåäóåò, ÷òî êàæäàÿ èç íàéäåííûõ
âåëè÷èí u
C
, i, u
L
ñîñòîèò èç äâóõ ñëàãàåìûõ, çàòóõàþùèõ ïî ýêñ-
ïîíåíòå ñ êîýôôèöèåíòàìè p
1
< 0 è p
2
< 0. Íà ðèñ. 6.12 ïîêàçàí
õàðàêòåð çàâèñèìîñòåé (6.46)%(6.48). Ìîìåíò âðåìåíè t
1
, ñîîò-
âåòñòâóþùèé òî÷êå ïåðåãèáà u
C
, ìàêñèìóìó |i| è íóëåâîìó çíà÷å-
íèþ u
L
îïðåäåëÿåòñÿ èç ðåøåíèÿ óðàâíåíèÿ di/ dt = 0, à ìîìåíò t
2
èç ðåøåíèÿ óðàâíåíèÿ du
L
/dt = 0:
2
121
121
1
ln;2.
p
ttt
ppp
==
-
(6.49)
Àíàëèç ïîëó÷åííûõ êðèâûõ ïîêàçûâàåò, ÷òî â ðàññìàòðèâàåìîì
ñëó÷àå ïðîèñõîäèò àïåðèîäè÷åñêèé ðàçðÿä åìêîñòè Ñ, ïðè÷åì â
èíòåðâàëå îò 0 äî t
1
ýíåðãèÿ W
C
ðàñõîäóåòñÿ íà ïîêðûòèå òåï-

170
ëîâûõ ïîòåðü â ðåçèñòèâíîì ñîïðîòèâëåíèè R è ñîçäàíèå ìàãíèò-
íîãî ïîëÿ â èíäóêòèâíîñòè (p
C
= u
C
i < 0; p
L
= u
L
i > 0). Â äàëü-
íåéøåì (ïðè t > t
1
) êàê ýíåðãèÿ ýëåêòðè÷åñêîãî ïîëÿ åìêîñòè W
C
,
òàê è çàïàñåííàÿ ê ìîìåíòó t = t
1
ìàãíèòíàÿ ýíåðãèÿ èíäóêòèâíî-
ñòè W
L
ðàñõîäóåòñÿ íà ïîêðûòèå òåïëîâûõ ïîòåðü â ñîïðîòèâëåíèè
R. Îòðèöàòåëüíîå çíà÷åíèå òîêà ñâèäåòåëüñòâóåò î ïðîòèâîïîëîæ-
íîì íàïðàâëåíèè òîêà ðàçðÿäà îòíîñèòåëüíî îïîðíîãî íàïðàâëå-
íèÿ.
Âî âòîðîì ñëó÷àå ïðè R < 2r, êîãäà êîðíè p
1
è p
2
íîñÿò êîìï-
ëåêñíî-ñîïðÿæåííûé õàðàêòåð,
2
2
1,2c
0
,
pjj
=-a±w-a=-a±w
(6.50)
ãäå
2
2
c
0
w=w-a
Ö íàçûâàþò ÷àñòîòîé ñîáñòâåííûõ çàòóõàþùèõ
êîëåáàíèé. Ðåøåíèå óðàâíåíèÿ (6.39) èìååò âèä (6.9)
(
)
ñâ
c
sin,
t
CC
uuAe
t
-a
==
w+q
(6.51)
ãäå A è q % ïîñòîÿííûå èíòåãðèðîâàíèÿ. Çàêîí èçìåíåíèÿ òîêà â
öåïè
( ) ( )
c
cc
sincos.
C
tt
du
iCAeAe
tt
dt
-a-a
==-a+w
w+qw+q
(6.52)
Ïîñòîÿííûå A è q îïðåäåëÿþòñÿ èç íà÷àëüíûõ óñëîâèé äëÿ u
C
è i
è çàêîíîâ êîììóòàöèè (6.1), (6.2):
(
)
(
)
( ) ( )
c
sin,
00
sincos.
00
CC
uuUA
iiAA
-+
-+
===q
ü
ý
==-aq+wq
þ
(6.53)
Îòñþäà
(
)
0c
c
;arctg.
AU
=wwq=
wa
Îêîí÷àòåëüíî óðàâíåíèÿ äëÿ u
C
, i è è ïðèíèìàþò âèä
( )
0
c
c
sin;
t
C
uUe
t
-a
w
=
w+q
w
(6.54)
t
u
C
()
t
i
()
t
-
U
0
U
1
U
-i
m
u
L
()
t
ui
,
t
1
t
2
t
u
C
()
t
i
()
t
0
U
ui
,
-U
u
C
( + )
tT
C
T
C
Ðèñ. 6.12 Ðèñ. 6.13
