Askeland D.R., Fulay P.P. Essentials of Materials Science & Engineering
Подождите немного. Документ загружается.


Strain-Rate Sensitivity (m) The strain-rate sensitivity (m) of stress is defined as:
m ¼
qðln sÞ
qðln
_
eÞ
ð8-2Þ
This describes how fast strain hardening occurs in response to plastic deformation. As
mentioned before, the mechanical behavior of sheet steels under high strain rates ð
_
eÞ is
important not only for shaping, but also for how well the steel will perform under high-
impact loading. The crashworthiness of sheet steels is an important consideration for
the automotive industry. Steels that harden rapidly under impact loading are useful in
absorbing mechanical energy.
A positive value of m implies that material will resist necking (Chapter 6). High
values of m and n mean the material can exhibit a better formability in stretching.
However, these values do not a¤ect the deep drawing characteristics. For deep drawin g,
the plastic strain ratio (r) is important. We define plastic strain ratio as:
r ¼
e
w
e
t
¼
ln
w
w
0
ln
h
h
0
ð8-3Þ
In this equation, w and h correspond to the width and thickness of the material being
processed and the subscript zero indicates original dimensions. Forming limit diagrams
are often used to better understand the formability of metallic materials. Overall, we
define formability of a material as the ability of a material to maintain its integrity
while being shaped.
Springback When a metallic material is deformed using a stress above its yield strength
to a higher level (s
1
in Figure 8-1(d)), the corresponding strain existing at stress s
1
is
obtained by dropping a perpendicular line to the x-axis (point e
total
). A strain equal to
(e
total
e
1
) is recovered since it is elastic in nature. The elastic strain that is recovered
after a material has been plastically deformed is known as springback [Figure 8-1(e)].
The occurrence of springback is extremely important for the formation of automotive
body panels from sheet steels along with many other applications. This e¤ect is also seen
in processing of polymeric materials processed, for example, by extrusion. This is because
many polymers are viscoelastic (Chapter 6) and recovery of elastic strain does occur.
TABLE 8-1 9 Strain-hardening exponents and strength coefficients of typical
metals and alloys
Metal Crystal Structure n K (MPa)
Titanium HCP 0.05 1207
Annealed alloy steel BCC 0.15 641
Quenched and tempered
medium-carbon steel BCC 0.10 1572
Molybdenum BCC 0.13 724
Copper FCC 0.54 317
Cu-30% Zn FCC 0.50 896
Austenitic stainless steel FCC 0.52 1517
Adapted from G. Dieter, Mechanical Metallurgy, McGraw-Hill, 1961, and other sources.
C HA P T E R 8 Strain Hardening and Annealing230

It is possible to account for springback in designing components; however, vari-
ability in springback makes this very di‰cult. For example, an automotive supplier will
receive coils of sheet steel from di¤erent steel manufacturers, and even though the specifi-
cations for the steel are identical, the springback variation in steels received from each
manufacturer (or even for di¤erent lots from the same manufacturer) will make it harder
to obtain cold worked components that have precisely the same shape and dimensions.
Bauschinger Effect Consider a material that has been subjected to tensile plastic de-
formation. Then, consider two separate samples ( A and B) of this material
that have been previously deformed. Test sample A in tension, and sample B under
compression. We notice that for the deformed material the flow stress in tension
(s
flow; tension
) for sample A is greater than the compressive yield strength (s
flow; compression
)
for sample B. This e¤ect, in which a material subjected to tension shows reduction in
compressive stren gth, is known as the Bauschinger e¤ect. Note that we are comparing
the yield strength of a material under compression and tension after the material has
been subjected to plastic deformation under a tensile stress. The Bauschinger e¤ect is
also seen on stress reversal. Consider a sample deformed under compression. We can
then evaluate two separate samples C and D of this material. The sample subjected to
another compressive test (C ) now shows a higher flow stress than that for the sample D
subjected to tensile stress. The Bauschinger e¤ect plays an important role in mechanical
processing of steels and other alloys.
8-2 Strain-Hardening Mechanisms
We obtain strengthening during deformation of a metallic material by increasing the
number of dislocations. Before deformation, the dislocation density is about 10
6
cm of
dislocation line per cubic centimeter of metal—a relatively small concentration of dis-
locations.
When we apply a stress greater than the yield strength, dislocations begin to slip
(Schmid’s Law, Chapter 4). Eventually, a dislocation moving on its slip plane encoun-
ters obstacles that pin the ends of the dislocation line. As we continue to apply the
stress, the dislocation attempts to move by bowing in the center. The dislocation may
move so far that a loop is produced. When the dislocation loop finally touches itself,
a new dislocation is created. The original dislocation is still pinned and can create
additional dislocation loops. This mechanism for generating dislocations is called a
Frank-Read source.
The dislocation density may increase to about 10
12
cm of dislocation line per cubic
centimeter of metal during strain hardening. As discussed in Chapter 4, dislocation
motion is the cause for the plastic flow that occurs in metallic materials; however, when
we have too many dislocations, they interfere with their own motions. An analogy for
this is when we have too many people in a room it is di‰cult for them to move around.
The result of increased dislocation density is an increased strength, but reduced ductil-
ity, for metallic materials that have undergone cold working or work hardening.
Ceramics contain dislocations and can even be strain-hardened to a small degree.
However, dislocations in ceramics are normally not very mobile. Polycrystalline ce-
ramics also contain porosity. As a result, ceramics behave as brittle materials and
significant deformation and strengthening by cold working are not possible. Likewise,
covalently bonded materials such as silicon (Si) are too brittle to workharden appreci-
ably. Glasses are amorphous and do not contain dislocations and therefore cannot be
strain hardened.
8-2 Strain-Hardening Mechanisms 231
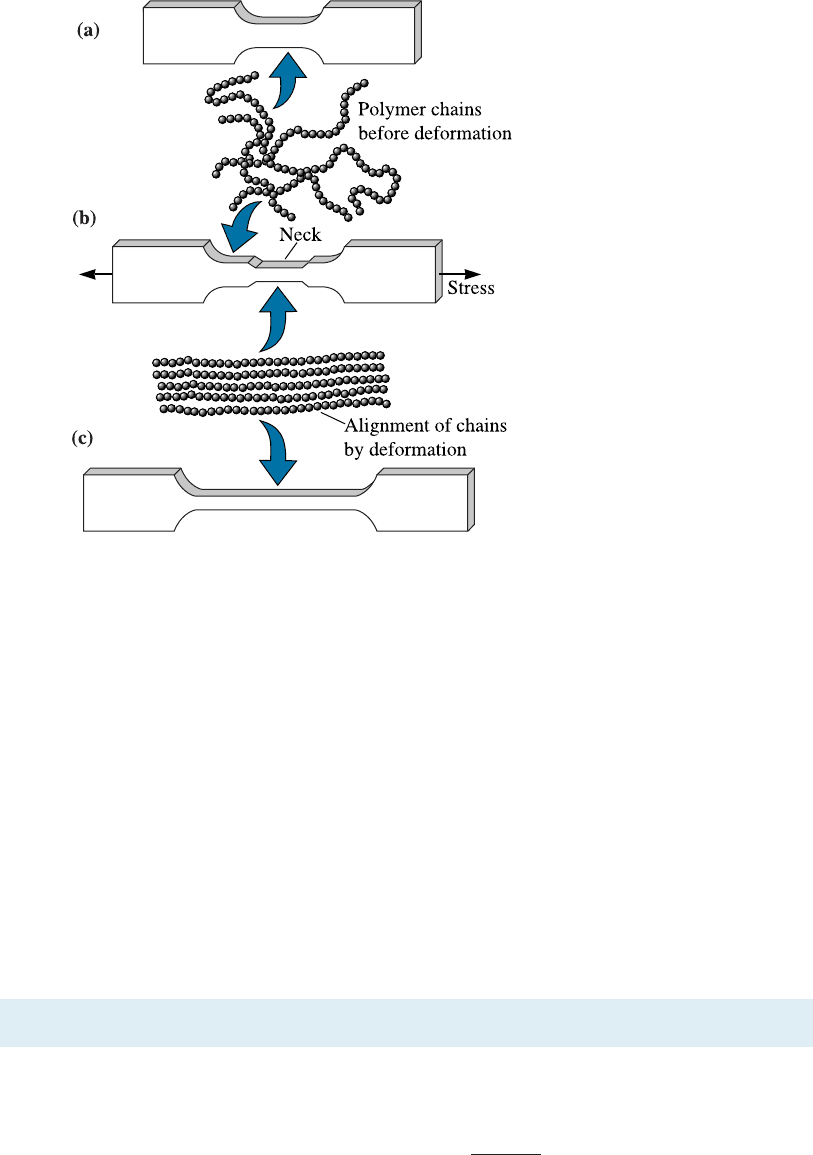
Thermoplastics are polymers such as polyethylene, polystyrene, and nylon. These
materials consist of molecules that are long spaghetti-like chains (Chapter 16). Thermo-
plastics will strengthen when they are deformed. However, this is not strain hardening
due to dislocation multiplication but, instead, strengthening of these materials involves
alignment and possibly localized crystallization of the long, chainlike molecules. When
a stress greater than the yield strength is applied to thermoplastic polymers such as
polyethylene, the van der Waals bonds (Chapter 3) between the molecules in di¤erent
chains are broken. The chains straighten and become aligned in the direction of the
applied stress (Figure 8-4). The strength of the polymer, particularly in the direction of
the applied stress, increases as a result of the alignment of polymeric chains in the di-
rection of the applied stress. The processing of polyethylene terephthalate (PET) bottles
made by the blow-stretch process involves such stress-induced crystallization. Thermo-
plastic polymers get stronger as a result of local alignments of polymer chains occurring
as a result of applied stress. This strength increase is seen in the stress-strain curve of
typical thermoplastics (Chapter 6).
8-3 Properties versus Percent Cold Work
By controlling the amount of plastic deformation, we control strain hardening. We
normally measure the amount of deformation by defining the percent cold work:
Percent cold work ¼
A
0
A
f
A
0
100 ð8-4Þ
where A
0
is the original cross-sectional area of the metal and A
f
is the final cross-
sectional area after deformation.
Figure 8-4
In an undeformed thermoplastic
polymer tensile bar, (a) the polymer
chains are randomly oriented.
(b) When a stress is applied, a
neck develops as chains become
aligned locally. The neck continues
to grow until the chains in the
entire gage length have aligned.
(c) The strength of the polymer is
increased.
C HA P T E R 8 Strain Hardening and Annealing232

The e¤ect of cold work on the mechanical properties of commercially pure cop-
per is shown in Figure 8-5. As the cold work increases, both the yield and the tensile
strength increase; however, the ductility decreases and approaches zero. The metal
breaks if more cold work is attempted. Therefore, there is a maximum amount of cold
work or deformation that we can perform on a metallic material before it becomes too
brittle and breaks.
Figure 8-5
The effect of cold work on the
mechanical properties of copper.
EXAMPLE 8-1 Cold Working a Copper Plate
A 1-cm-thick copper plate is cold-reduced to 0.50 cm, and later further reduced
to 0.16 cm. Determine the total percent cold work and the tensile strength of
the 0.16-cm plate. (See Figure 8-6.)
SOLUTION
Note that, because the width of the plate does not change during rolling, the
cold work can be expressed as the percentage reduction in the thickness t.
We might be tempted to determine the amount of cold work accomplished
in each step, that is:
%CW¼
A
0
A
f
A
0
100 ¼
t
0
t
f
t
0
100 ¼
1cm 0:50 cm
1cm
100
¼ 50%
%CW¼
A
0
A
f
A
0
100 ¼
t
0
t
f
t
0
100 ¼
0:50 cm 0:16 cm
0:50 cm
100
¼ 68%
Figure 8-6
Diagram showing the
rolling of a 1-cm plate
to a 0.16-cm plate
(for Example 8-1).
8-3 Properties versus Percent Cold Work 233

We might then be tempted to combine the two cold work percentages (50% þ
68% ¼ 118%) to obtain the total cold work. This would be incorrect.
Our definition of cold work is the percenta ge change between the original
and final cross-sectional areas; it makes no di¤erence how many intermediate
steps are involved. Thus, the total cold work is actually
%CW¼
t
0
t
f
t
0
100 ¼
1cm 0:16 cm
1cm
100 ¼ 84%
and, from Figure 8-5, the tensile strength is about 565 MPa.
We can predict the properties of a metal or an alloy if we know the amount of cold
work during processing. We can then decide whether the component has adequate
strength at critical locations.
When we wish to select a material for a component that requires certain minimum
mechanical properties, we can design the deformation process. We first determine the
necessary percent cold work and then, using the final dimensions we desire, calculate
the original metal dimensions from the cold work equation.
EXAMPLE 8-2
Design of a Cold Working Process
Design a manufacturing process to produce a 0.1-cm-thick copper plate having
at least 448 MPa tensile strength, 414 MPa yi eld strength, and 5% elongation.
SOLUTION
From Figure 8-5, we need at least 35% cold work to produce a tensile strength
of 448 MPa and 40% cold work to produce a yield strength of 414 MPa,
but we need less than 45% cold work to meet the 5% elongation requirement.
Therefore, any cold work between 40% and 45% gives the required mechanical
properties.
To produce the plate, a cold-rolling process would be appropriate. The
original thickness of the copper plate prior to rolling can be calculated from
Equation 8-4, assuming that the width of the plate does not change. Because
there is a range of allowable cold work—between 40% and 45%—there is a
range of initial plate thicknesses:
%CW
min
¼ 40 ¼
t
min
cm 0:1cm
t
min
cm
100; 9 t
min
¼ 0:167 cm
%CW
max
¼ 45 ¼
t
max
cm 0:1cm
t
max
cm
100; 9 t
max
¼ 0:182 cm
To produce the 0.1-cm copper plate, we begin with a 0.167- to 0.182-cm copper
plate in the softest possible condition, then cold roll the plate 40% to 45% to
achieve the 0.1 cm thickness.
C HA P T E R 8 Strain Hardening and Annealing234
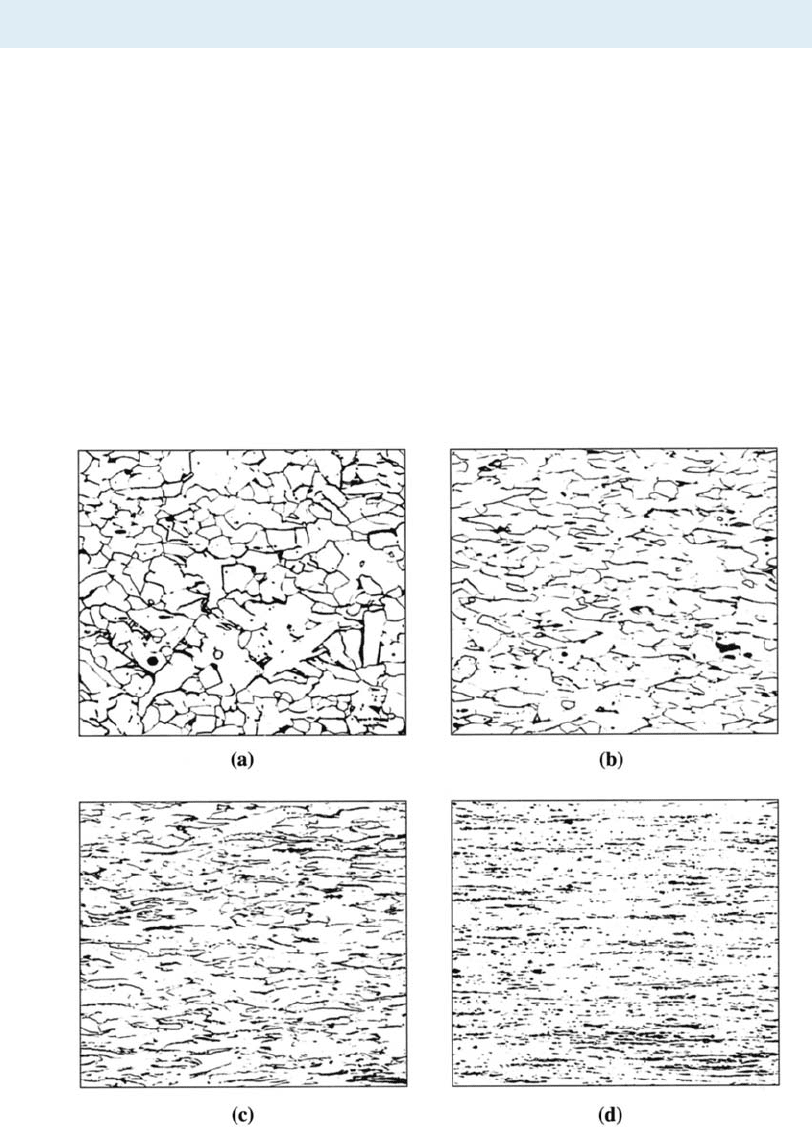
8-4 Microstructure, Texture Strengthening, and Residual Stresses
During plastic deformation using cold or hot working, a microstructure consisting of
grains that are elongated in the direction of the stress applied is often produced (Fig-
ure 8-7).
Anisotropic Behavior During deformation, the grains rotate as well as elongate, caus-
ing certain crystallographic directions and planes to become aligned with the direction
in which stress is applied. Consequently, preferred orientations, or textures, develop and
cause anisotropic behavior.
In processes such as wire drawing and extrusion, a fiber texture is produced. The
term ‘‘fiber’’ refers to the way grains in the metallic material which become elongated in
a direction parallel to the axis of the wire or an extruded product. In BCC metals,
h110i directions line up with the axis of the wire. In FCC metals, h111i or h100i
directions are aligned. This gives the highest strength along the axis of the wire or
the extrudate (product being extruded, such as a tube), which is what we desire.
Figure 8-7 The fibrous grain structure of a low carbon steel produced by cold working:
(a) 10% cold work, (b) 30% cold work, (c) 60% cold work, and (d) 90% cold work (250).
(Source: From ASM Handbook Vol. 9, Metallography and Microstructure, (1985) ASM
International, Materials Park, OH 44073. Used with permission.)
8-4 Microstructure, Texture Strengthening, and Residual Stresses 235
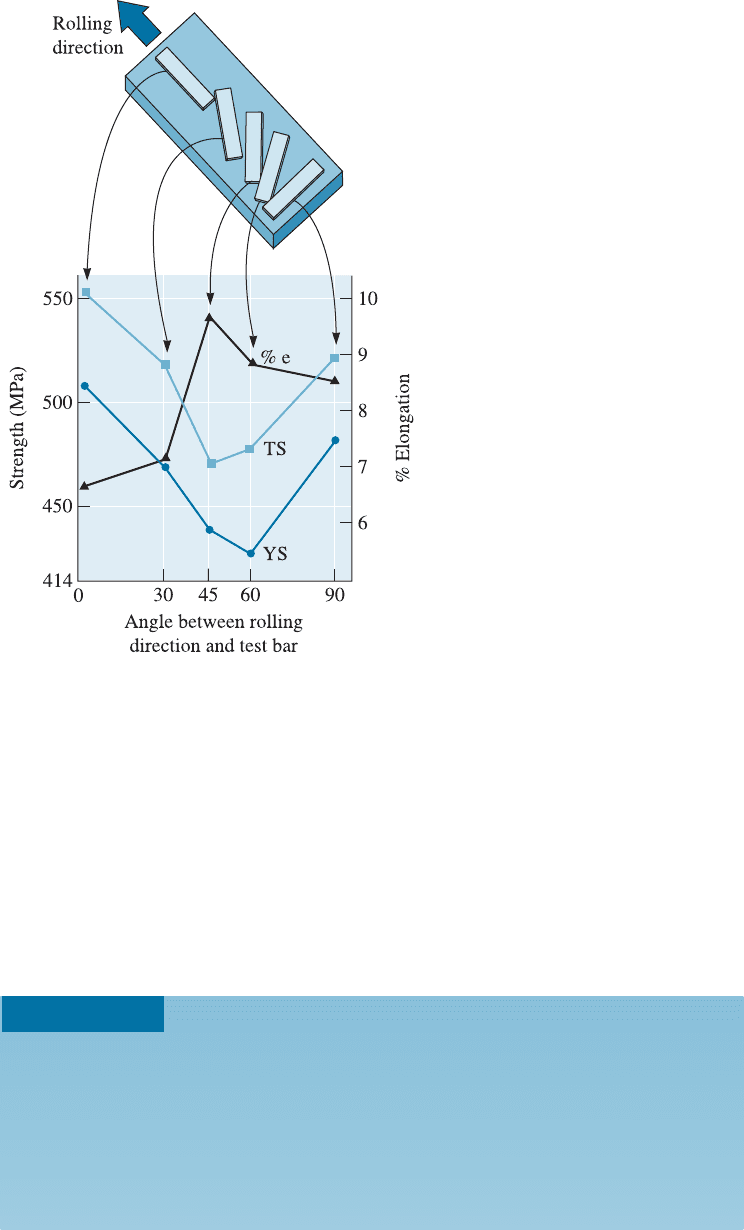
As mentioned previously, a somewhat similar e¤ect is seen in thermoplastic mate-
rials when they are drawn into fibers or other shapes. The cause, as discussed before, is
that polymer chains line up side-by-side (i.e., form crystalline regions) along the length
of the fiber. As in metallic materials, the strength is greatest along the axis of the poly-
mer fiber.
In processes such as rolling, grains become oriented in a preferred crystallographic
direction and plane, giving a sheet texture. The properties of a rolled sheet or plate
depend on the direction in which the property is measured. Figure 8-8 summarizes the
tensile properties of a cold worked aluminum-lithium (Al-Li) alloy. For this alloy,
strength is highest parallel to the rolling direction, whereas ductility is highest at a 45
angle to the rolling direction. The strengthening that occurs by the development of
anisotropy or of a texture, is known as texture strengthening.
Figure 8-8
Anisotropic behavior in a rolled
aluminum-lithium sheet material
used in aerospace applications. The
sketch relates the position of tensile
bars to the mechanical properties
that are obtained.
EXAMPLE 8-3
Design of a Stamping Process
One method for producing fans for cooling automotive and truck engines is
to stamp the blades from cold-rolled steel sheet, then attach the blades to a
‘‘spider’’ that holds the blades in the proper position. A number of fan blades,
all produced at the same time, have failed by the initiation and propagation
of a fatigue crack transverse to the axis of the blade (Figure 8-9). All other
fan blades perform satisfactorily. Provide an explanation for the failure of the
blades and redesign the manufacturing process to prevent these failures.
C HA P T E R 8 Strain Hardening and Annealing236

SOLUTION
There may be several expla nations for the failure of the blades—for example,
the wrong type of steel may have been selected, the dies used to stamp the
blades from the sheet may be worn, or the clearance between the parts of the
dies may be incorrect, producing defects that initiate fatigue failure.
The failures could also be related to the anisotropic behavior of the steel
sheet caused by rolling. To achieve the best performance from the blade, the
axis of the blade should be aligned with the rolling direction of the steel sheet.
This procedure produces high strength along the axis of the blade and, by
assuring that the grains are aligned with the blade axis, reduces the number
of grain boundaries along the leading edge of the blade that might help initiate
a fatigue crack. Suppose your examination of the blade using, for example,
pole figure analysis or metallographic analysis, indicates that the steel sheet
was aligned 90
from its usual position during stamping. Now the blade has a
low strength in the critical direction and, in addition, fatigue cracks will more
easily initiate and grow. This mistake in manufacturing can cause failures and
injuries to mechanics performing maintenance on automobiles.
You might recommend that the manufacturing process be redesigned to
assure that the blades cannot be stamped from misaligned sheet. Perhaps spe-
cial guides or locking devices on the die will assure that the die is properly
aligned with the sheet.
Figure 8-9
Orientations of samples
(for Example 8-3).
Residual Stresses A small portion of the applied stress—perhaps about 10%—is
stored in the form of residual stresses within the structure as a tangled network of dis-
locations. The residual stresses increase the total energy of the structure. The presence
of dislocations increases the total internal energy of the structure. The higher the extent
of cold working, the higher would be the level of total internal energy of the material.
Residual stresses generated by cold working may not always be desirable and can be
relieved by a heat treatment known as stress-relief anneal (Section 8-6). As will be dis-
cussed shortly, in some instances we deliberately create residual compressive stresses at
the surface of materials to enhance their mechanical properties.
The residual stresses are not uniform throughout the deformed metallic material.
For example, high compressive residual stresses may be present at the surface of a rol-
led plate and high tensile stresses may be stored in the center. If we machine a small
amount of metal from one surface of a cold-worked part, we remove metal that con-
tains only compressive residual stresses. To restore the balance, the plate must distort.
If there is a net compressive residual stress at the surface of a component, this may be
beneficial from a viewpoint of mechanical properties since any crack or flaw on the
8-4 Microstructure, Texture Strengthening, and Residual Stresses 237

surface will not likely grow. This is why any residual stresses, originating from cold
work or any other source, a¤ect the ability of the part to carry a load (Figure 8-10). If a
tensile stress is applied to a material that already contains tensile residual stresses, the
total stress acting on the part is the sum of the applied and residual stresses. If, how-
ever, compressive stresses are stored at the surface of a metal part, an applied tensile
stress must first balance the compressive residual stresses. Now the part may be capable
of withstanding a larger load. In Chapters 6 and 7, we learned that fatigue is a common
mechanism of failure for load-bearing components. Sometimes, components that are
subject to fatigue failure can be strengthened by shot peening. Bombarding the surface
with steel shot propelled at a high velocity introduces compressive residual stresses at
the surfa ce that increase the resistance of the metal surface to fatigue failure (Chapter
7). The following example explains the use of shot peening.
Figure 8-10 The compressive residual stresses can be harmful or beneficial. (a) A bending
force applies a tensile stress on the top of the beam. Since there are already tensile residual
stresses at the top, the load-carrying characteristics are poor. (b) The top contains compressive
residual stresses. Now the load-carrying characteristics are very good.
EXAMPLE 8-4
Design of a Fatigue-Resistant Shaft
Your company has produced several thousand shafts that have a fatigue
strength of 138 MPa. The shafts are subjected to high-bending loads during
rotation. Your sales engineers report that the first few shafts placed into service
failed in a short period of time by fatigue. Design a process by which the re-
maining shafts can be salvaged by improving their fatigue properties.
SOLUTION
Fatigue failures typically begin at the surface of a rotating part; thus, increas-
ing the strength at the surface improves the fatigue life of the shaft. A variety
of methods might be used to accomplish this.
If the shaft is made of steel, we could carburize the surface of the part
(Chapter 5). In carburizing, carbon is di¤used into the surface of the shaft.
After an appropriate heat treatment, the higher carbon at the surface increases
the strength of the surface and, perhaps more importantly, introduces com-
pressive residual stresses at the surface.
We might consider cold working the shaft; cold working increases the yield
strength of the metal and, if done properly, introduces compressive residual
stresses. However, the cold work also reduces the diameter of the shaft and,
because of the dimensional change, the shaft may not be able to perform its
function.
C HA P T E R 8 Strain Hardening and Annealing238
Another alternative would be to shot peen the shaft. Shot peening intro-
duces local compressive residual stresses at the surface without changing the
dimensions of the part. This process, which is also inexpensive, might be su‰-
cient to salvage the remaining shafts.
8-5 Characteristics of Cold Working
There are a number of advantages and limitations to strengthening a metallic material
by cold working or strain hardening:
9
We can simultaneously strengthen the metallic material and produce the desired
final shape.
9
We can obtain excellent dimensional tolerances and surface finishes by the cold-
working process.
9
The cold-working process is an inexpensive method for producing large numbers
of small parts, since high forces and expensive forming equipment are not needed. Also,
no alloying elements are needed, which means lower-cost raw materials can be used.
9
Some metals, such as HCP magnesium, have a limited number of slip systems
and are rather brittle at room temperature; thus, only a small degree of cold working
can be accomplished.
9
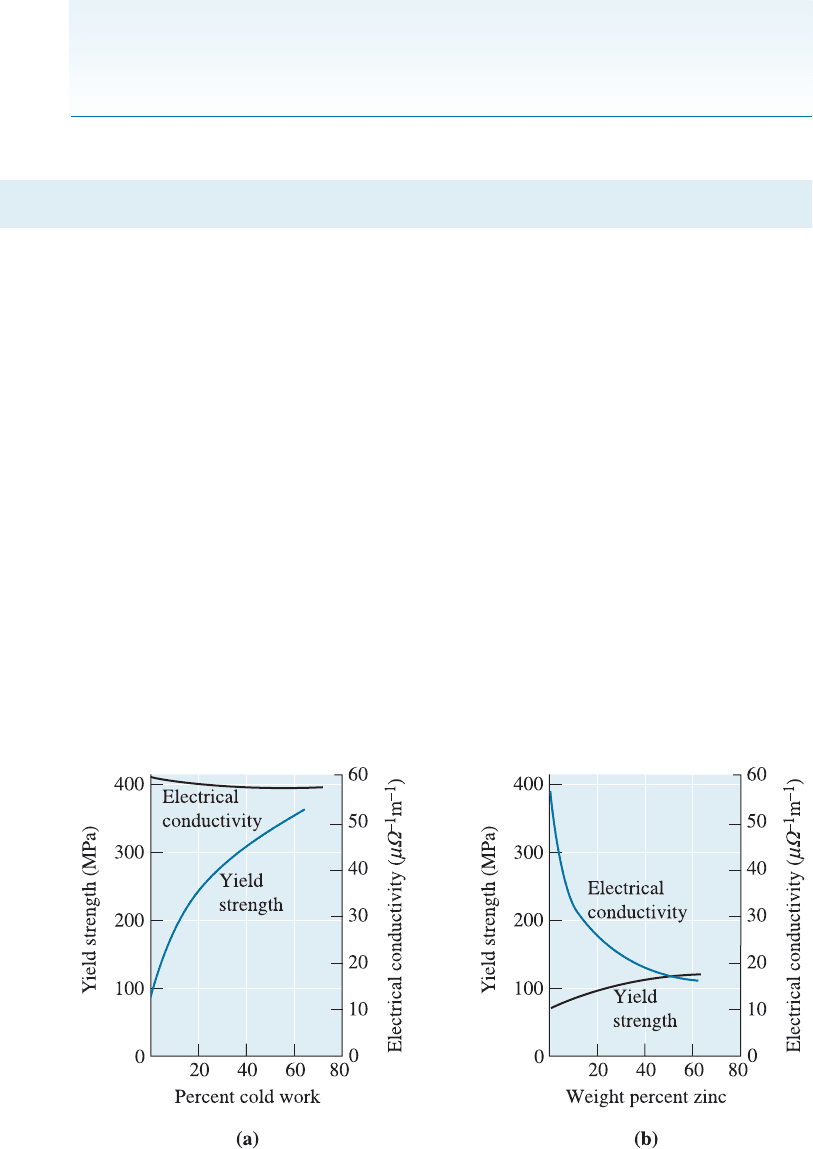
Ductility, electrical conductivity, and corrosion resistance are impaired by cold
working. However, since the extent to which electrical conductivity is reduced by cold
working is less than that for other strengthening processes, such as introducing alloying
elements (Figure 8-11), cold working is a satisfactory way to strengthen conductor ma-
terials, such as the copper wires used for transmission of electrical power.
Figure 8-11 A comparison of strengthening copper by (a) cold working and (b) alloying with
zinc. Note that cold working produces greater strengthening, yet has little effect on electrical
conductivity.
8-5 Characteristics of Cold Working 239
