Асанов А.З. Моделирование и анализ динамических систем
Подождите немного. Документ загружается.


использовать те обобщенные переменные системы, для которых
выполняются законы сохранения и которые не претерпевают разрыва
непрерывности при скачкообразном изменении входных воздействий.
Это условие приводит к тому, что за координаты вектора состояния
следует принимать выходные сигналы динамических элементов,
обладающих физическим свойством накапливать кинетическую,
потенциальную, электрическую и другую энергию, положение и т.п.
5.3.1. Особенности составления уравнений состояния для
механических систем
Выбор переменных состояния для механических систем в общем
случае подчиняется указанным выше рекомендациям. Как правило, при
рассмотрении механических систем в качестве переменных состояния
используются такие переменные как линейные
перемещение, скорость перемещения, ускорение
перемещения, угол поворота вала, угловая скорость,
угловое ускорение, сила, момент силы и т.д. Именно
через эти переменные выражаются потенциальная и
кинетическая энергии механической системы.
Подробнее эти вопросы рассматривались в разделе 2.4.2
Для иллюстрации рассмотрим механическую
систему, состоящую из пружины с коэффициентом упругости , груза с
массой и демпфера с коэффициентом демпфирования
Требуется найти уравнения состояния, описывающие движение системы
под воздействием внешней силы .
Очевидно, что в качестве переменных состояния целесообразно выбрать
линейное перемещение и скорость перемещения , т.к.
через эти переменные можно выразить все силы воздействующие на
рассматриваемую динамическую систему. Введение других переменных не
требуется, достаточно тех, что ввели (рассматриваемая динамическая
система является системой 2-го порядка).
Силы, взаимодействующие в этой системе, можно представить так:
- сила воздействия пружины;
- сила воздействия груза (элемента массы);
- сила воздействия демпфера.
Очевидно, что , где - внешняя сила,
81

или
Последнее уравнение при использовании введенных переменных
состояния и учета того, что , можно представить так:
или
Последние уравнения представляют собой искомое описание состояния
механической системы, изображенной на рис.5.3.1.
5.3.2. Особенности составления уравнений состояния для
электрических цепей
Применительно к электрическим цепям можно сформулировать
следующие рекомендации по выбору переменных состояния.
Состояние электрической системы можно характеризовать
параметрами, определяющими энергию, запасенную в элементах системы. В
общем случае это заряд и магнитный поток , связанные с током и
напряжением следующими формулами
(5.3.1)
Положим далее, что рассматриваемая система является линейной и
стационарной, т.е. будем полагать, что значения сопротивлений , емкостей
и индуктивностей не изменяются с течением времени.
Тогда выражения (5.3.1) упрощаются
(5.3.2)
В этом случае в качестве переменных состояния можно выбрать
напряжения на конденсаторах и токи через катушки индуктивности
, а для составления уравнений состояния можно в осп ол ь зо в а ться
законами Ома и Кирхгофа для мгновенных значений т о к о в и напряжений.
Из соотношений (5.3.2) в этом случае необходимо выразить токи чере3
конденсаторы и напряжения на катушках индуктивности через вы бр ан ны е
переменные состояния (напряжения и токи ) и вы хо дн ы е
82

(5.3.3)
(5.3.4)
Если электрическая цепь содержит катушек индуктивности и
конденсаторов, то в электрической цепи определяется соответствующее
число напряжений и токов на реактивных элементах цепи, которые в
совокупности подчиняются законам Кирхгофа. Эти напряжения и токи могут
служить переменными состояния этой цепи.
Функции и являются алгебраическими даже в случае
нелинейной и нестационарной цепи, т.к. уравнения составлялись с
использованием мгновенных значений токов и напряжений.
Для иллюстрации рассмотрим пример описания электрических цепей в
пространстве состояний.
Рассмотрим пассивный многополюсник (рис.5.3.1) со стационарными
параметрами, который представляет собой систему 2-го порядка.
Состояние рассматриваемой цепи определяется энергией, запасенной в
реактивных элементах и , и входным сигналом
Энергия, запасенная в индуктивности,
определяется током в индуктивности
, а энергия запасенная в конденсаторе
- напряжением :
Выберем эти переменные в качестве
переменных состояния
Уравнение Кирхгофа для данной цепи будет иметь вид:
Учитывая и , получим соотношения
и
После преобразований уравнения состояния окончательно примут вид
сйгналы, т.е. получить уравнения вида
Рис. 5.3.1. Схема многополюсника.
83

В соответствии с заданной схемой (рис. 5.3.1) выходные сигналы можно
описать следующими соотношениями:
Из последних соотношений после замены переменных легко прийти к
стандартной записи уравнений в пространстве состояний - заданная
электрическая цепь описывается матричными уравнениями вида
где
5.3.3. Особенности составления уравнений состояния для
электромеханических систем
Особенности составления уравнений состояний для
электромеханических систем проистекают из того факта, что в таких
системах существуют и взаимодействуют как механические элементы, так
и электрические цепи. Отсюда очевидно то обстоятельство, что необходим
учет особенностей как той, так и другой частей электромеханической
системы.
Для примера рассмотрим составление описания двигателя постоянного
тока в пространстве состояний.
Процессы в электродвигателе постоянного тока характеризуются
следующими соотношениями:
уравнение электрической цепи ;
уравнение механической цепи ;
уравнение момента сопротивления ;
уравнение момента двигателя ;
уравнение э.д.с. двигателя
Здесь в этих уравнениях:
- ток якоря двигателя; - активное сопротивление (Ом) и
индуктивность (Гн) якорной цепи; - напряжение, В; - э.д.с. д вига теля ,
В; - действующий момент двигателя, Нм; - момент с о п р о т и в л е н и я
84

на валу двигателя, Нм: - момент инерции, приведенный к валу
двигателя; - угловая скорость вращения вала двигателя, рад/сек;
магнитный поток возбуждения двигателя, Вб; - конструктивный
коэффициент двигателя ( - соответственно число пар полюсов,
активных проводников и параллельных ветвей обмотки якоря). Обычно,
Выберем в качестве переменных состояния (ток якоря
электродвигателя - характеризует электрическую часть системы) и
(угловая скорость вращения механической части системы). Связи между
электрической и механической частями системы описываются уравнениями
для момента сопротивления и момента двигателя.
Преобразуя приведенные выше уравнения, приводя дифференциальные
уравнения к нормальной форме Коши и осуществляя необходимые замены
переменных - получим уравнения состояния этого электродвигателя в
следующем виде:
Вводя обозначения которые в
электротехнике имеют четко выраженный физический смысл, получаем
уравнения состояния с матрицами
Матрицы и будут определяться, исходя из условий наблюдения.
Так, если выходной величиной будет угловая скорость , то матрица
примет вид , если же в качестве выходной величины будет
рассматриваться действующий момент двигателя ,то
85

5.4. Формирование уравнений состояний по
дифференциальному уравнению
Наиболее простым методом описания динамических систем является
поэлементное описание системы, когда каждый элемент системы
описывается своим дифференциальным (реже алгебраическим) уравнением, а
взаимосвязи элементов в системе описываются уравнениями связи. Сами
же дифференциальные уравнения элементов формируются на основе тех
фундаментальных физических законов, на действии которых базируется
работа элемента динамической системы. В общем случае дифференциальное
уравнение элемента системы и, тем более, дифференциальное уравнение
самой системы представляют собой уравнение высокого порядка.
Поставим задачу формирования уравнений состояния системы в виде
уравнений (5.2.6) и (5.2.7) по известному дифференциальному уравнению
п-го порядка.
Рассмотрим дифференциальное уравнение с постоянными
коэффициентами для динамической системы с одним входом и одним
выходом
(5.4.1)
где и - постоянные коэффициенты.
Введем систему следующих допущений и обозначений
(5.4.2)
Последнее уравнение получено из уравнения (5.4.1). Это уравнение
можно переписать с учетом введенных ранее в (5.4.2) о б о з н а ч е н и й
следующим образом;
Тогда вся система соотношений (5.4.2) может быть представлена в
следующем виде (здесь и далее для лучшей иллюстрации н езав иси м ы й
аргумент / при переменных величинах упущен):
86
Структурная схема, отображающая ту же систему уравнений, имеет вид,
показанный на рис. 5.4.2, где использованы обозначения:
Полученная форма уравнений состояния (5.4.3) и (5.4.4) носит
название строчной управляемой фробениусовой канонической формы [11] и
является одной из самых распространенных на практике форм. Другие
87
(5.4.3)
(5.4.4)
Таким образом, дифференциальному уравнению (5.4.1) в пространстве
состояний соответствуют уравнения
(5.4.5) где
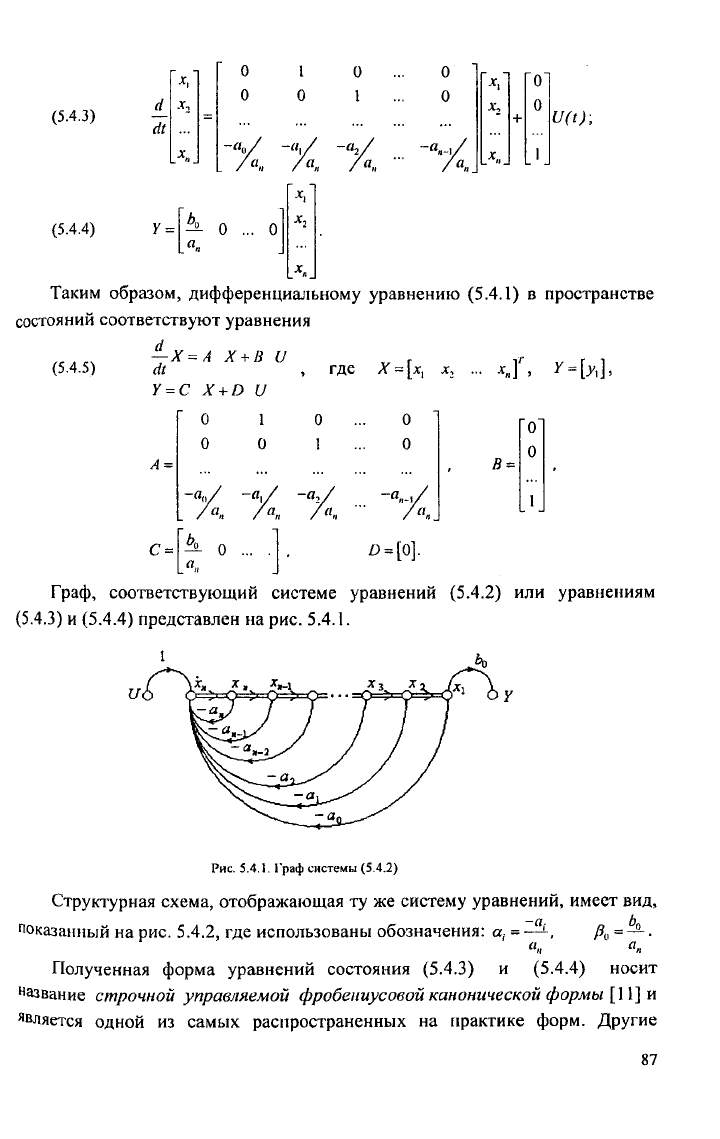
Граф, соответствующий системе уравнений (5.4.2) или уравнениям
(5.4.3) и (5.4.4) представлен на рис. 5.4.1.
Рис. 5.4.1. Граф системы (5.4.2)
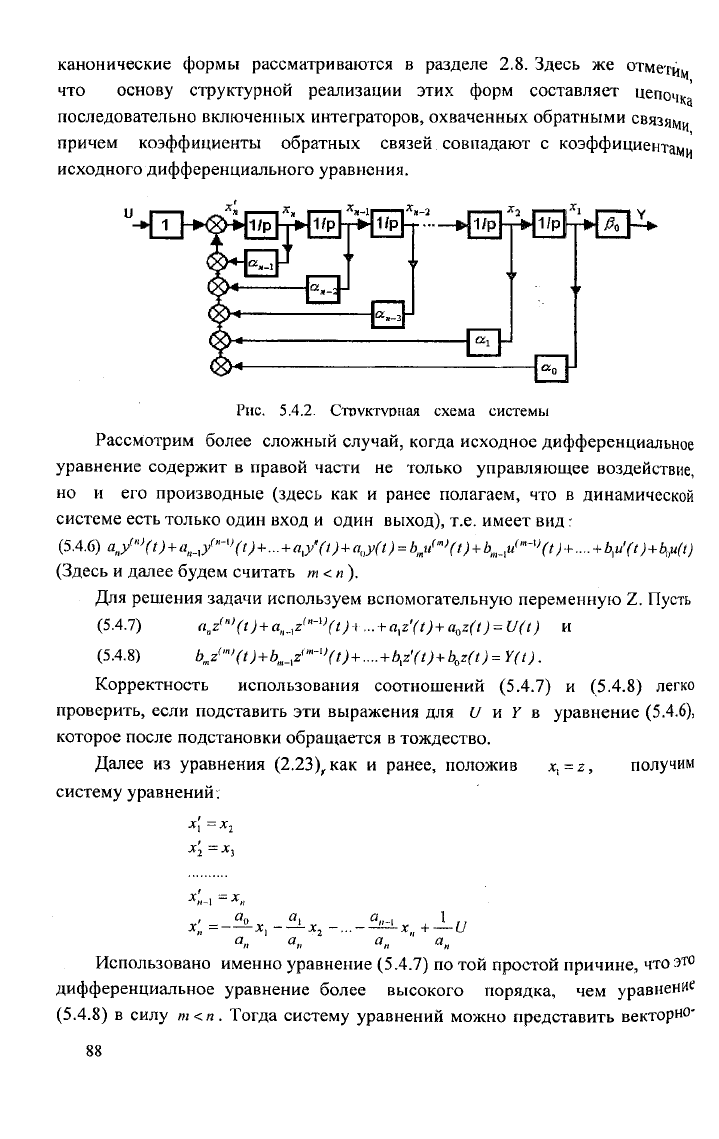
канонические формы рассматриваются в разделе 2.8. Здесь же отметщ,
что основу структурной реализации этих форм составляет цепочка
последовательно включенных интеграторов, охваченных обратными связями
причем коэффициенты обратных связей совпадают с коэффициентами
исходного дифференциального уравнения.
Рассмотрим более сложный случай, когда исходное дифференциальное
уравнение содержит в правой части не только управляющее воздействие,
но и его производные (здесь как и ранее полагаем, что в динамической
системе есть только один вход и один выход), т.е. имеет вид г
(5.4.6)
(Здесь и далее будем считать ).
Для решения задачи используем вспомогательную переменную Z. Пусть
(5.4.7) и
(5.4.8)
Корректность использования соотношений ( 5 .4 .7 ) и ( 5 .4 .8 ) легко
проверить, если подставить эти выражения для и в уравнение (5.4 .6 ),
которое после подстановки обращается в тождество.
Далее из уравнения (2.23), как и ранее, положив , получим
систему уравнений;
Использовано именно уравнение ( 5 .4 .7 ) по той простой причине, что это
дифференциальное уравнение более высокого порядка, чем у р а в н е н и е
( 5 .4 .8 ) в силу . Тогда систему уравнений можно представить в е к т о р н 0'
Рис. 5.4.2. Стпуктуоная схема системы
88

матричной форме
а уравнение (5.4.8) может быть представлено в следующем виде
Таким образом, для исходного дифференциального уравнения (5.4.6)
η-го порядка матричные уравнения состояния имеют тот же стандартный вид
уравнений (5.4.5), но состав матриц. уже другой. Конкретно
Полученная форма уравнений состояния также относится к строчным
управляемым фробениусовым каноническим формам. Граф и структурная
схема, соответствующие полученным уравнениям,представлены на рис. 5.4.3
и 5.4.4.
89
Рис. 5.4.3. Граф системы

Рис. 5.4.4. Структурная схема системы
5.5. Формирование уравнений состояний но передаточной
функции
Нахождение уравнений состояния динамической системы в
пространстве состояний по известной передаточной функции системы
является неоднозначной процедурой из-за произвола выбора переменных
состояния.
Одним из наиболее распространенных является метод, использующий в
качестве системы переменных состояния фазовые координаты.
Рассмотрим решение задачи формирования уравнений состояний для
системы с одним входом и одним выходом и имеющей передаточную
функцию вида
(5.5.1)
где и - изображения по Лапласу выходного и входного сигналов
системы соответственно.
Соответствующее этой передаточной функции д и ф ф е р е н ц и ал ь н о е
уравнение динамической системы запишется в виде:
(5.5.2)
Здесь - выходной сигнал системы; - входной сигнал системы.
Из сравнения (5.5.2) и (5.46) видно, что они тождественны друг ДРУГУ·
Поэтому дальнейший переход к уравнениям состояния полностью
совпадает с методом, изложенным в предыдущем разделе.
В результате получим, что матрицы уравнений состояния д и н а м и ч е с к о й
90
