Асанов А.З. Моделирование и анализ динамических систем
Подождите немного. Документ загружается.


(5.5.3)
Граф динамической системы, описываемой передаточной функцией
(5.5.1) или, что равнозначно,
уравнениями состояния с
матрицами (5.5.2), приведен на рис.
5.5.1.
Ранее уже отмечалось, что
одной и той же передаточной
функции можно поставить в
соответствие уравнения состояния
вида (2.26), но с различными
матрицами Так, если
в дифференциальном уравне
нии (5.5.2), соответствующем
передаточной функции (5.5.1) переменные состояния определить
равенствами,
то матрицы уравнений состояния динамической системы принимают вид
(5.5.4)
Элементы матрицы связаны с коэффициентами
исходной передаточной функции следующими соотношениями:
системы имеют вид .
91
Рис. 5.5.1. Граф системы

Граф, соответствующий системе с матрицами вида (5.5.4),представлен
на рис. 5.5.2. Уравнения состояния динамической системы с такими
матрицами носят название
строчной наблюдаемой
фробениусовой канонической формы.
Нетрудно увидеть, что хотя в
(5.5.3) и (5.5.4) матрицы систем
одинаковы, но весьма сильно
различаются матрицы
Другой способ формирования
уравнений состояний динамической
системы в пространстве
состояний по известной
передаточной функции системы заключается в разложении
передаточной функции на элементарные дроби и в последующем
представлении совокупности этих дробей в пространстве состояний.
Рассмотрим систему с одним входом и одним выходом, передаточная
функция которой представляет собой отношение двух полиномов
(5.5.5)
Полагаем, что . Если предположить, что корни полинома
различные, то полином можно представить в виде:
(5.5.6)
где - корни характеристического уравнения
В этом случае передаточная функция раскладывается в виде
(5.5.7) где
при при
Постоянные коэффициенты и могут быть найдены также с
помощью метода неопределенных коэффициентов.
Рис. 5.5.2. Граф системы
92

Изображение выходного сигнала можно представить в виде
(5.5.8)
Соответствующий этому выражению граф модели динамической
системы представлен на рис. 5.5.3.
Каждая из переменных удовлетворяет
дифференциальному уравнению 1 порядка:
(5.5.9)
или, иначе говоря, удовлетворяет частной
передаточной функции
Сигнал на выходе всей динамической
системы будет описываться формулой
(5.5.10)
Уравнения состояния, соответствующие исходной передаточной
функции и графу системы на рис. 5.5.3, будут иметь вид
(5.5.11)
Матрица в этом случае носит название диагональной формы
Жордана. В случае, если корни многочлена знаменателя не являются
различными, т.е. являются кратными, или в случае комплексных корней,
метод разложения передаточной функции на элементарные дроби приводит
к более сложной матрице модели динамической системы. .
5.6. Формирование уравнений состояний по структурной
схеме
Структурная схема (или граф) динамической системы дает условное
Пифическое изображение взаимосвязанных элементов, составляющих
систему и различающихся своими динамическими свойствами. При этом в
93
Рис. 5.5.3. Граф системы

графическом изображении системы указываются и преобразования, которые
подвергается сигнал при прохождении через тот или иной элемент.
Формирование уравнений состояния системы по известной структуру
схеме (графу) может осуществляться несколькими способами.
Среди них можно отметить:
1) получение передаточной функции системы и последующий переход ογ
передаточных функций к уравнениям в пространстве состояний (см
раздел 5.5);
2) представление структурной схемы системы в виде совокупности типовых
динамических звеньев I и II порядков, описание этих типовых звеньев в
пространстве и последующее использование правил формирования
уравнений состояния системы по известным уравнениям подсистем (см.
раздел 5.7);
3) детализация структурной схемы системы с тем, чтобы блоки схемы
описывали простые одинарные операции (сложение, вычитание,
умножение, дифференцирование, интегрирование и т.п.) и дальнейшая
запись системы уравнений преобразования.
Для иллюстрации последнего способа рассмотрим пример, когда
известна структурная схема некоторого динамического объекта
(рис.5.6.1)
Когда структура динамической системы детализована до простых
операций сложения, вычитания, умножения, дифференцирования,
интегрирования и т.д., то наиболее целесообразным является выбор в
качестве переменных состояния сигналов на выходе блоков интегрирования.
Сами же уравнения состояний формируются далее по структурной схеме
системы.
В нашем конкретном случае, по структурной схеме (или графу) системы
можно записать следующие уравнения:
94
Рис. 5.6.1. Структурная схема и граф системы

(5.6.1)
Отсюда легко установить, что в уравнении состояния объекта матрицы
имеют вид:
Нетрудно увидеть, что получился результат, совпадающий с
результатом примера в разделе 2.4.3. Это говорит о том, что исходная
структурная схема соответствовала электродвигателю постоянного тока.
5.7. Формирование уравнений состояний системы по
известным уравнениям подсистем
Сложные динамические комплексы образуются совокупностью более
простых динамических подсистем. Как правило, при этом используются
типовые соединения: последовательные, параллельные и встречно
параллельные (соединения с обратными связями). Тогда правомерен вопрос
об эквивалентном описании подсистем соединенных между собой тем или
иным видом соединения.
Полагаем, что каждая динамическая подсистема описана в пространстве
состояний матричными уравнениями вида
(5.7.1)
Принадлежность векторов и матриц к той или иной динамической
подсистеме, участвующей в соединении будем указывать индексами 1 и 2.
Соединения динамических подсистем обычно описываются с
помощью метода расширения фазового пространства. В этом случае для
описания объединенных подсистем вводится расширенный вектор состояния
(5.7.2)
95
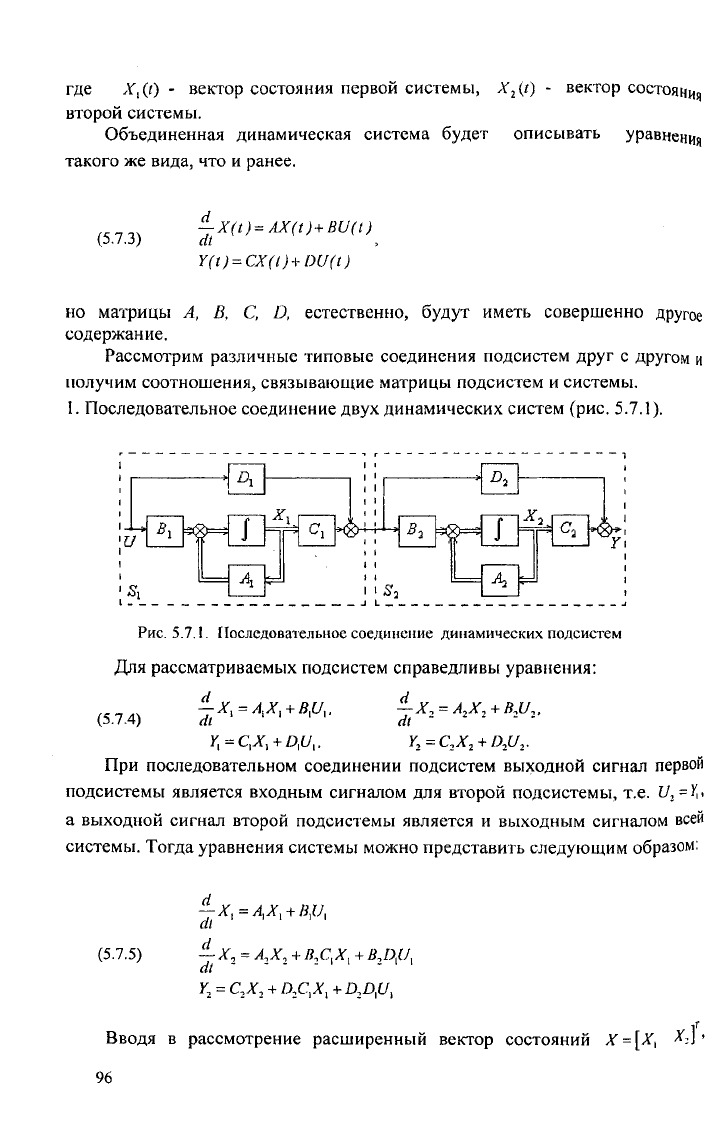
Для рассматриваемых подсистем справедливы уравнения:
(5.7.4)
При последовательном соединении подсистем выходной сигнал первой
подсистемы является входным сигналом для второй подсистемы, т.е. и г=У,<
а выходной сигнал второй подсистемы является и выходным сигналом всей
системы. Тогда уравнения системы можно представить следующим образом:
(5.7.5)
Вводя в рассмотрение расширенный вектор состояний
96
где - вектор состояния первой системы, - вектор состояния
второй системы.
Объединенная динамическая система будет описывать уравнения
такого же вида, что и ранее.
(5.7.3)
но матрицы естественно, будут иметь совершенно другое
содержание.
Рассмотрим различные типовые соединения подсистем друг с другом и
получим соотношения, связывающие матрицы подсистем и системы.
1. Последовательное соединение двух динамических систем (рис. 5.7.1).
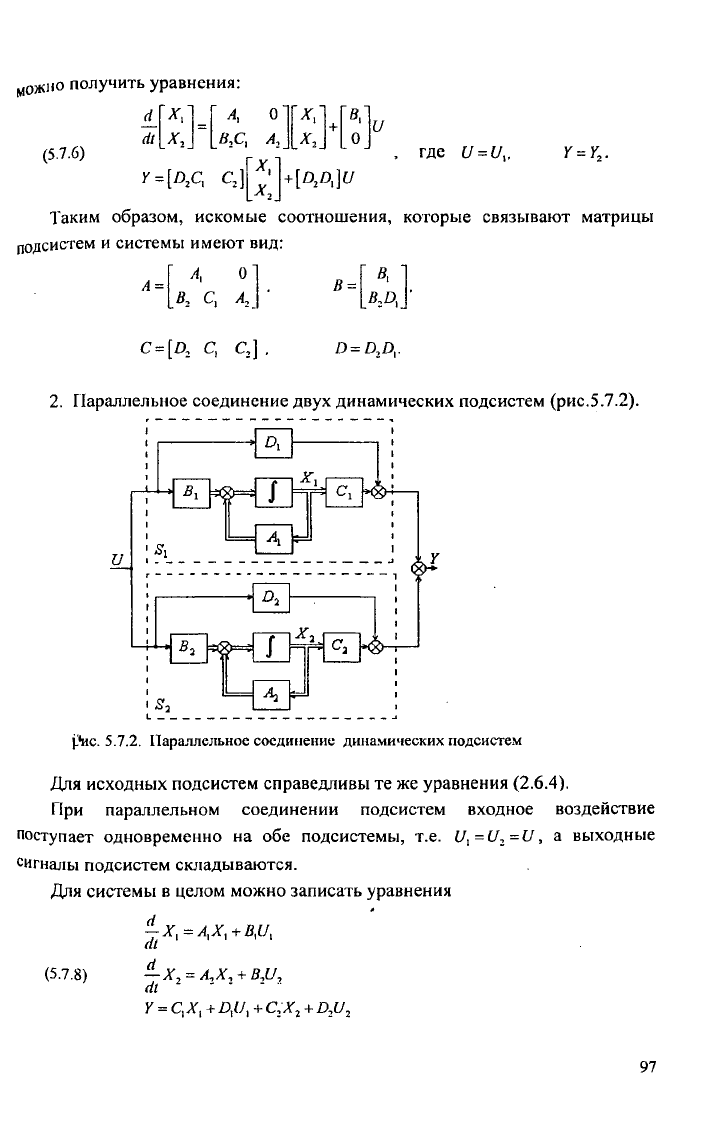
Для исходных подсистем справедливы те же уравнения (2.6.4).
При параллельном соединении подсистем входное воздействие
поступает одновременно на обе подсистемы, т.е. , а выходные
сигналы подсистем складываются.
Для системы в целом можно записать уравнения
(5.7.8)
97
(5.7.6) где
Таким образом, искомые соотношения, которые связывают матрицы
подсистем и системы имеют вид:
2. Параллельное соединение двух динамических подсистем (рис.5.7.2).
можн° получить уравнения:
рис. 5.7.2. Параллельное соединение динамических подсистем
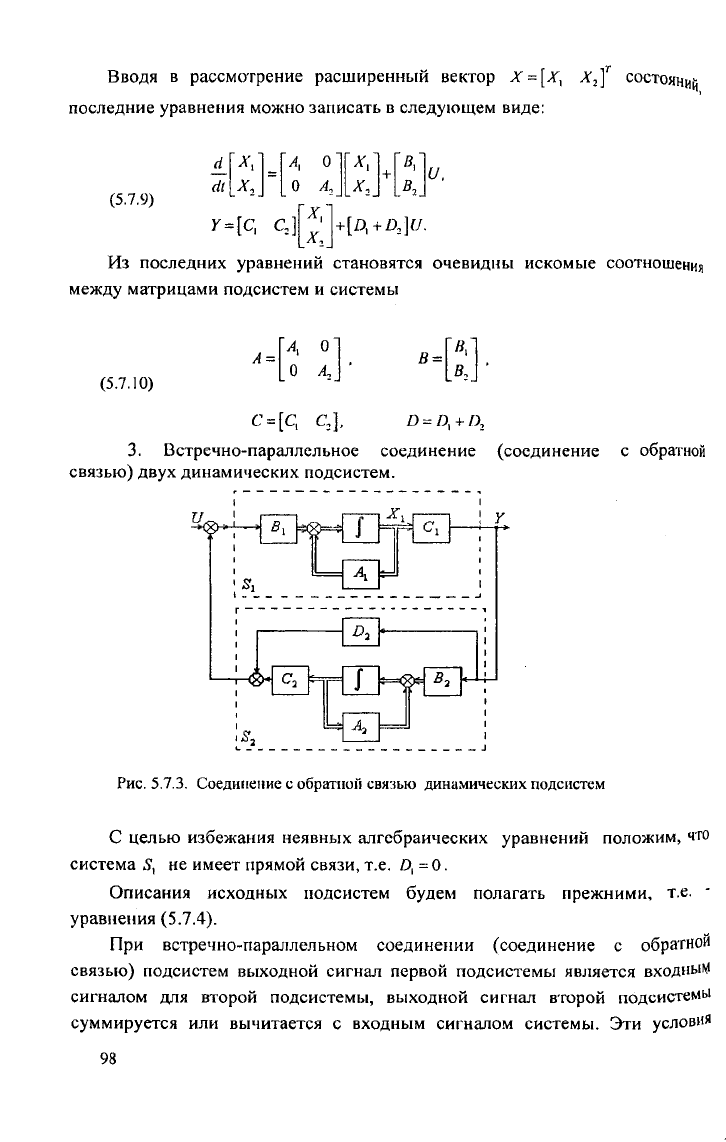
Рис. 5.7.3. Соединение с обратной связью динамических подсистем
С целью избежания неявных алгебраических уравнений положим, что
система не имеет прямой связи, т.е.
Описания исходных подсистем будем полагать прежними, т.е. ·
уравнения (5.7.4).
При встречно-параллельном соединении (соединение с обратной
связью) подсистем выходной сигнал первой подсистемы является входным
сигналом для второй подсистемы, выходной сигнал второй подсистемы
суммируется или вычитается с входным сигналом системы. Эти условия
Вводя в рассмотрение расширенный вектор состояний
последние уравнения можно записать в следующем виде:
(5.7.9)
Из последних уравнений становятся очевидны искомые соотношения
между матрицами подсистем и системы
(5.7.10)
3. Встречно-параллельное соединение (соединение с обратной
связью) двух динамических подсистем.
98

аналитически можно зап исать с помощью уравнений:
Тогда для всей системы в целом можно записать следующие уравнения:
или
Вводя в рассмотрение расширенный вектор состояний ,
последние уравнения можно записать в следующем виде:
(5.7. К)
Из этих уравнений легко искомые соотношения между матрицами
подсистем и системы. С учетом того, что на входе системы сигнал обратной
связи может суммироваться с входным сигналом системы (положительная
обратная связь) или вычитаться (отрицательная обратная связь), в
обобщенном виде искомые матричные соотношения принимают вид:
(5.7.12)
Здесь верхний знак соответствует положительной обратной связи, а
нижний - отрицательной обратной связи.
5.8. Определение передаточных функций но уравнениям
состояний
Одной из классических форм описания динамических систем является
описание системы с помощью передаточной функции.
Передаточной функцией динамической системы принято
называть отношение изображений по Лапласу выходного и входного
сигналов системы при нулевых начальных условиях
(5.8.1)
99

где представляют собой
изображения по Лапласу для выходного и входного сигналов.
Пусть известны уравнения состояний динамической системы в
пространстве состояний
(5.8.2)
Здесь - векторные функции времени.
Найдем передаточную функцию передаточной системы, заданной
уравнениями (5.8.2). Применим к этим уравнениям преобразование
Лапласа. С учетом свойств преобразования Лапласа получатся уравнения:
(5.8.3)
где - начальные условия.
Из первого уравнения выразим вектор
(5.8.4)
и подставим во второе уравнение:
(5.8.5)
Здесь и далее - единичная матрица соответствующего размера.
При нулевых (по определению передаточной функции) начальных
условиях, т.е. при , можно найти аналитическое выражение
передаточной функции динамической системы, определяемое через
параметры уравнений состояния:
(5.8.6)
В общем случае, когда входное воздействие и выходной сигнал
являются векторами (например, как представлено на рис.5.8.1),
представляет собой матрицу и называется матричной передаточной
функцией (МПФ). Элементами матрицы являются скалярные
передаточные функции , характеризующие операторные
коэффициенты передачи от -го входа системы до ее -го выхода.
100
