Асанов А.З. Моделирование и анализ динамических систем
Подождите немного. Документ загружается.


6. Анализ динамических систем
6.1. Решение уравнений состоянии динамических систем
Рассмотрим систему -го порядка, имеющую, в общем случае,
входов и выходов и которая описывается уравнениями
(6.1.1)
где
Пусть известны параметры системы, т.е. известны матрицы ;
известен вектор входных сигналов ; известны начальные условия -
значения вектора в момент времени , т.е. известен вектор
Поставим задачу определения выходного сигнала системы . Для
решения этой задачи необходимо найти решение первого уравнения
из (6.1.1), а затем подставить во второе уравнение (6.1.1).
Для нахождения вектора переменных состояния необходимо
решить систему неоднородных дифференциальных уравнений состояния,
которая в матричной форме имеет вид'
(6.1.2)
Решение такого матричного уравнения может быть представлено в виде
суммы двух составляющих (здесь полная аналогия с решением
обыкновенного дифференциального уравнения в классической математике).
Первая составляющая - свободная составляющая представляет собой
решение однородного матричного дифференциального уравнения (при
нулевом входном сигнале )
(6.1.3) или
Вторая составляющая - вынужденная составляющая
представляет собой частное решение неоднородного матричного
Дифференциального уравнения (6.1.2).
Таким образом, общее решение уравнения (6.1.2) будет иметь вид
(6.1.4)
Воспользуемся аналогичностью матричного и скалярного
121

дифференциальных уравнений и прежде, чем решать уравнение (6.1,3)
рассмотрим одномерную систему I порядка, уравнение которой имеет вид
Это уравнение с разделяющимися переменными и его решение имеет вид
Отсюда, при
Значение определяется из начальных условий при . Нетрудно
получить, что
Таким образом, свободная составляющая решения для скалярного
дифференциального уравнения имеет вид
Совершенно аналогично можно получить решение матричного
уравнения (6.1.3)
(6.1.5)
где коэффициенты матрицы представляют собой постоянные величины.
Введем обозначение и назовем переходной
матрицей. В общем случае, когда коэффициенты матрицы зависят от
времени, определение будет следующим:
Матрица , где , называется переходной
матрицей состояния нестационарной динамической системы.
Таким образом, свободная составляющая решения матричного
уравнения (6.1.2), или, что одно и то же, решение матричного уравнения
(6.1.3), будет иметь вид:
(6.1.6)
Физический смысл только что введенной переходной матрицы
очевиден из последнего соотношения: матрица определяет
переход из некоторого начального состояния в текущее состояние
, т.е. определяет процесс отработки системой начальных отклонении.
Этим объясняется ее название - переходная матрица состояния.
Нетрудно увидеть, что если , т.е. система стационарна, то
(6.1.7)
Ограничиваясь рассмотрением только стационарных систем, привеДеМ
122

здесь основные свойства переходной матрицы [4, 8]:
1. 2.
(6. 1.8)
3. 4.
Способы вычисления переходной матрицы будут даны в
следующем разделе.
Для нахождения вынужденной составляющей решения
матричного уравнения (6.1.2) воспользуемся методом вариации параметров.
В этом случае будем искать в таком же виде, что и свободная
составляющая
(6.1.9)
Здесь, в отличие от свободной составляющей, полагаем, что
неизвестная функция параметров, зависящих от времени.
Очевидно, что составляющая решения должна удовлетворять
уравнению состояния (6.1.2):
Подставив в последнее уравнение выражение (6.1.9), и, используя
третье и четвертое свойства из (6.1.8), получим
Отсюда:
Постоянная интегрирования определяется из начальных условий.
Если предположить, что входной сигнал при , то для физически
реализуемых систем получается, что
Таким образом, с учетом (6.1.9) вынужденная составляющая решения
матричного уравнения (6.1.2) имеет вид:
или с учетом второго свойства переходной матрицы из (6.1.8)
123

Окончательно, переменная состояния системы, представляющая собой
полное решение матричного дифференциального уравнения (6.1.2),
записывается в следующем виде
(6.1.11)
Выходной сигнал динамической системы теперь может быть найден из
второго уравнения (6.1.1)
или
Выходной сигнал системы также можно представить в виде суммы
составляющих
Первая составляющая определяется только параметрами
системы и начальными условиями . Вторая составляющая
зависит от параметров системы и входного сигнала
. Такое представление выходного сигнала справедливо только для
линейных систем.
Окончательно полное выражение для выходного сигнала
(6.1.12)
где - свободная составляющая выходного сигнала,
- вынужденная составляющая выходного
сигнала.
В стационарных динамических системах функции зависят не от
абсолютных значений и , а от разности этих аргументов . С учетом
этого обстоятельства выражения (
6.1.11) и (6.1.12) можно записать
следующим образом
(6.1.13)
(6.1.14)
При исследовании динамических систем весьма часто используют такие
характеристики системы, как импульсные (весовые), переходные,
передаточные и частотные.
(6.1.10)
124

Для определения импульсной (весовой) характеристики можно
воспользоваться выражением (6.1.14) для выходного сигнала системы. По
определению весовая (импульсная характеристика) функция одномерной
системы равна выходному сигналу системы при подаче на её вход
дельта функции (начальные условия нулевые).
Весовая функция многомерной системы определяется аналогичным
образом. Но в этом случае из-за многомерности системы приходится иметь
дело с матрицей весовых функций (МВФ) системы (6.1.1).
Для линейных многомерных систем выходной сигнал определяется
матричной формой интеграла Дюамеля
(6.1.15)
Из формулы (6.1.12) при нулевых (по определению) начальных условиях
и полагая, что , получим
Преобразуя последнее выражение, получим соотношение, аналогичное
интегралу Дюамеля (6.1.15):
(6.1.16)
Здесь учтено, что матрица не зависит от времени, а также
использовано фильтрующее свойство дельта функции.
Сравнивая формулы (6.1.15) и (6.1.16), нетрудно записать выражение
для матричной весовой функции системы:
(6.1.17)
Матричная частотная характеристика (МЧХ) может быть найдена
преобразованием Фурье матричной весовой функции (МВФ) или по
известной матричной передаточной функции (МПФ).
Как ранее уже выводилось (см. раздел 5.8), матричная передаточная
функция определяется выражением:
Из последнего выражения заменой можно найти матричную
частотную характеристику
125

6.2. Методы вычисления переходной матрицы
Начнем рассмотрение методов вычислений переходных матриц с
простейших случаев.
1. Пусть динамическая система стационарна, т.е. элементы матрицы не
зависят от времени. В этом случае для вычисления переходной матрицы
можно воспользоваться одним из следующих методов.
6.2.1. Метод разложения в ряд
Переходную матрицу можно представить в виде бесконечного ряда
(6.2.1)
Ограничившись некоторым числом членов ряда и произведя
суммирование, можно найти приближенное выражение для переходной
матрицы . Этот метод трудоемок, и может быть рекомендован при
использовании вычислительной техники.
6.2.2. Метод, основанный на преобразовании Лапласа
Применим преобразование Лапласа к однородному матричному
дифференциальному уравнению состояния
или
Отсюда
(6.2.2)
Применив к обеим частям уравнения (6.2.2) обратное преобразование
Лапласа, получим
(6.2.3)
Сравнивая уравнения (6.2.3) и (6.1.5), приходим к выводу, что
переходная матрица может быть определена и таким выражением
(6.2.4)
Такой метод нахождения переходной матрицы удобен при решении
многих задач, но очевидной сложностью является в этой формуле
нахождение обратной матрицы
6.2.3. Метод, основанный на теореме Сильвестера
Суть используемой теоремы заключается в следующем [18]: пусть
требуется получить некоторую функцию от матрицы , которую
126

можно представить в виде матричного многочлена.
Приведем формулировку теоремы Сильвестера для случая различных
собственных чисел матрицы .
Из теоремы следует, что функция может быть вычислена по
формуле
(6.2.5)
где - собственные числа матрицы
(6.2.6)
Другой формулой для вычисления является выражение
Здесь обозначает так называемую присоединенную матрицу
, где - соответствующее алгебраическое дополнение,
характеристический полином матрицы
Уравнение (6.2.5) в этом случае принимает вид;
Если среди собственных чисел матрицы есть кратные, то формулы
для вычисления значительно усложняются.
Пусть, например, собственные числа имеют кратность
Тогда формула для вычисления примет вид
(6.2.7)
Уравнение (6.2.7) представляет собой вырожденную форму теоремы
Сильвестера.
В случае, когда требуется вычислить переходную матрицу, принимаем
и ведем расчеты по приведенным выше формулам (6.2.5),
(6.2.7).
2. Пусть динамическая система нестационарная, т.е. элементы матрицы
зависят от времени. В этом случае, если выполняется условие
127

коммутативности для матрицы т.е. выполняется условие
для любых и переходная матрица может быть
вычислена по формуле [4]:
(6.2.8)
В общем случае, при невыполнении условия коммутативности
переходная матрица системы не описывается формулой (6.2.8). В этом
случае доказывается, что переходная матрица системы может быть
определена с помощью соотношения
(6.2.9)
где - интегральный оператор.
Ряд в правой части (6.2.9) является квадратной матрицей и называется
матрицантом.
Основное свойство матрицанта
Таким образом, понятно, что
Нетрудно увидеть, что если - постоянная матрица из (6.2.9)
получается ранее приведенная формула (6.2.1).
6.2.4. Примеры вычисления переходных матриц
Пример. Найти переходную матрицу при
Характеристическое уравнение
Тогда и составляющая , порождаемая
простым корнем , равна
128

С учетом Тогда
6.3. Применение операционного исчисления к решению
дифференциальных уравнений
Преобразование Лапласа составляет основу так называемого
операционного исчисления, под которым понимается совокупность методов
прикладного математического анализа, позволяющих экономными и
непосредственно ведущими к цели средствами получать решения линейных
дифференциальных, разностных и некоторых типов интегральных
уравнений. Операционное исчисление нашло широкое применение в теории
автоматического управления, где с его помощью производится анализ
переходных и установившихся процессов в автоматических системах.
Суть операционного метода заключается в следующем.
Пусть известна некоторая функция - оригинал действительной
переменной . Каждой такой функции с помощью преобразования Лапласа
можно поставить в соответствие другую функцию - изображение
комплексной переменной . Используя свойства преобразования Лапласа,
операциям дифференцирования и интегрирования оригинала (свойство 2)
можно поставить в соответствие в пространстве изображений более простые
алгебраические операции умножения и деления изображения на . Это
позволяет дифференциальное уравнение, записанное относительно искомой
функции , заменить в пространстве изображений на алгебраическое
Уравнение относительно изображения Решив это алгебраическое
Уравнение и найдя , можно получить изображение решения исходного
Дифференциального уравнения. Для определения самого решения можно
129
воспользоваться обратным преобразованием Лапласа.
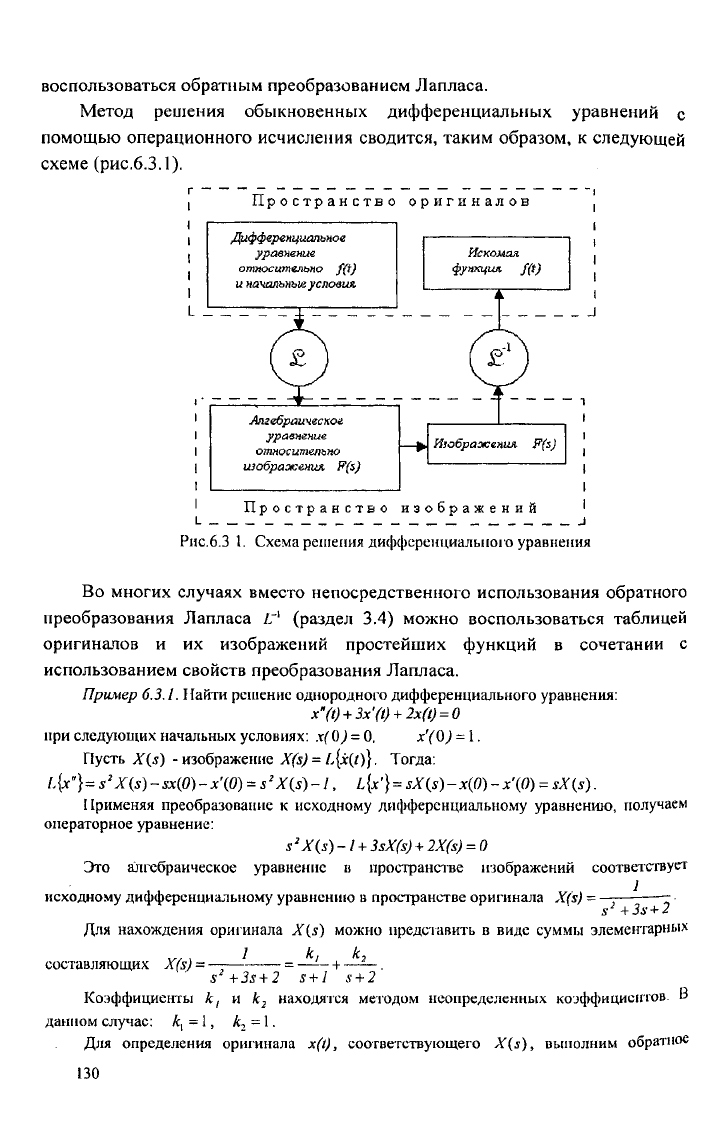
Метод решения обыкновенных дифференциальных уравнений с
помощью операционного исчисления сводится, таким образом, к следующей
схеме (рис.6.3.1).
Во многих случаях вместо непосредственного использования обратного
преобразования Лапласа (раздел 3.4) можно воспользоваться таблицей
оригиналов и их изображений простейших функций в сочетании с
использованием свойств преобразования Лапласа.
Пример 6.3.1. Найти решение однородного дифференциального уравнения:
при следующих начальных условиях:
Пусть - изображение . Тогда:
Применяя преобразование к исходному дифференциальному уравнению, получаем
операторное уравнение:
Это алгебраическое уравнение в пространстве изображений со ответствует
исходному дифференциальному уравнению в пространстве оригинала
Д л я нахождения оригинала можно представить в виде суммы э ле мен тар ны х
составляющих
Коэффициенты и находятся методом неопределенных ко эф ф и ци ен то в В
данном случае: ,
Для определения оригинала , соответствующего , выполним об ратн ое
Пространство оригиналов
Дифференциальное
уравнение
относительно
и начальные условия
Искомал
фунхцш.
Алгебраическое
уравнение
относительно
изображения
Изображения
Пространство изображений
Рис.6.3 1. Схема решения дифференциального уравнения
130
