Асанов А.З. Моделирование и анализ динамических систем
Подождите немного. Документ загружается.


51
всевозможных комбинаций из трех несоприкасающихся контуров;
- минор -го прямого пути - значение для той части сигнального
графа, которая не соприкасается с -м прямым путем (его можно вычислить,
если удалить -й прямой путь вместе с дугами, которые с этим путем
соприкасаются и рассмотреть оставшуюся часть графа);
- коэффициенты передачи замкнутых контуров, имеющиеся в графе
(обход каждого контура производится в одном направлении и не проходит
дважды через одну и ту же вершину);
* - означает, что суммирование проводится только для произведений
несоприкасающихся контуров, т.е. контуров не имеющих ни одной общей
вершины.
Пример. Определим передаточную функцию для графа на рис.2.5.4, т.е.
передаточную функцию модели электродвигателя постоянного тока.
В графе имеем три контура с коэффициентами передачи
Определитель графа А получается следующим:
В графе имеем всего один прямой путь с коэффициентом передачи
и минором . Тогда искомая передаточная функция
графа (а значит и модели электродвигателя постоянного тока) после
простейших алгебраических преобразований выражается формулой:

3. Основные формы моделей скалярных динамических
систем
Любая динамическая система является сложной по своему поведению
системой. Как правило, такая система характеризуется
целым рядом различных величин, переменных и т.д.
Решая те или иные частные задачи, нет необходимости
учитывать всю совокупность таких характеристик и
переменных - достаточно использовать некоторое
подмножество. Поэтому математические модели системы учитывают и
описывают только определённые стороны системы. По таких математических
моделей множество. Среди математических моделей динамической системы
достаточно часто используют модели, где учитывается одно входное
воздействие и одна выходная (управляемая) переменная (рис. 3.0.1). Такие
системы принято называть скалярными системами [8, 11] (или SISO - в
англоязычной литературе).
Таким образом, для скалярной системы характерно наличие одного
входного (управляющего) сигнала. При этом состояние всей динамической
системы может описываться переменными состояниями при
Существуют различные способы описания свойств и характеристик
скалярной системы. Наиболее употребительными в практике являются
следующие формы моделей, которые могут быть названы классическими.
3.1. Дифференциальные уравнения n-го порядка
В этом случае динамическая система описывается неоднородным
дифференциальным уравнением вида:
• (3.1.1)
где - выходная (управляемая) величина, u(t) - входное (управляющее)
воздействие, - коэффициенты дифференциальные
уравнения.
В общем случае, и являются функциями времени - это
соответствует нестационарным динамическим системам. Для стационарных
систем характерно то, что и представляют собой постоянные величины.
Уравнение (3.1.1) устанавливает связь между входным сигналом и
выходной (управляемой) величиной . Поэтому такое уравнение часто
52
Рис.3.0.1. Скалярная
система

называют вход-выходным описанием динамической системы. Эта форма
математического описания динамических систем может быть подучена из
поэлементного описания системы путём исключения всех промежуточных
переменных.
Пример. Пусть поэлементное описание динамической системы представлено
системой уравнений:
(3.1.2)
гае - входной сигнал, - выходной сигнал, - промежуточная переменная,
осуществляющая связь между элементами системы.
Требуется получить вход-выходное описание в виде (3.1.1).
Решение. Продифференцируем второе уравнение (3.1.2), чтобы избавиться от интеграла.
Для упрощения выкладок и для лучшей иллюстрации сути процедуры введем оператор
. Тогда уравнения (3.1.2) с учётом дифференцирования можно записать:
Далее необходимо осуществить преобразование с тем, чтобы исключить из
уравнений промежуточную переменную и получить соотношение, связывающее
выходную переменную с входной переменной
Умножим каждый из членов первого уравнения на оператор , а каждый из
членов второго уравнения на и сложим эти уравнения. Тогда
или
или с учётом того, что
, что является искомым результатом.
Процедура использования в данном примере справедлива для любых
двух дифференциальных уравнений с постоянными коэффициентами. Если
означает операторную функцию от р, то уравнение можно символически
записать так:
Умножим первое уравнение на , а второе - на и вычтем одно из
Другого. Так как , то получим: ,
аналогично
В общем случае, при наличии системы из дифференциальных
уравнений процедура получения вход-выходного описания аналогична
53

приведённой выше.
Пусть
Так как операторные функции зависят только от , то можно показать, что
решение можно получить, используя правило Крамера:
J
где - операторная функция, определяемая определителем:
- операторная функция, которая является - алгебраическим
дополнением , т.е. является определителем с вычеркнутыми - й
строкой и -м столбцом, умноженным на
Получение вход-выходного описания для систем с переменными
коэффициентами (нестационарные системы) гораздо сложнее.
3.2. Временные характеристики динамических систем
Известно, что решение дифференциальных уравнений вида (3.1.1) при
заданных начальных условиях единственно. Это свойство можно
использовать и описывать динамические системы не дифференциальным
уравнением, а его решением при определенных (заданных, типовых) входных
воздействиях.
При исследовании динамических систем чаще всего в качестве типовых
воздействий используются единичная ступенчатая функция и дельта
функция
Переходная характеристика
Аналитическое выражение единичной ступенчатой функции имеет вид:
Переходная характеристика (переходная функция) системы
определяется как реакция динамической системы на единичное ступенчатое
54

в х о д н о е воздействие при нулевых начальных условиях.
Аналитически - это есть решение дифференциального уравнения (3.1.1)
при нулевых начальных условиях и при условии
Весовые функции
Другим типовым сигналом, часто используемым при исследованиях
динам ических систем, является дельта-функция :
и
Весовая функция (весовая характеристика) системы определяется как
реакция динамической системы при подаче вход дельта - импульса
Аналитически - это есть решение дифференциального уравнения (3.1.1)
при нулевых начальных условиях и при условии, что
Очевидно, для физически реализуемых систем при , т.к.
выходной сигнал не может появиться раньше входного. Кроме того, можно
доказать, что весовая функция устойчивых систем является затухающей
функцией.
Учитывая, что взаимосвязь между и в классе обобщенных
функций можно представить соотношением , нетрудно записать
соотношения, связывающую функции и
или
Переходная и весовая функции динамической системы являются ее
временными характеристиками.
При известных временных характеристиках (моделях) можно вычислить
реакцию системы на любой произвольный сигнал . Для этого можно
использовать интеграл Дюамеля
П ример вычисления переходной функции. Найти переходную характеристику
(функцию) динамического звена, описываемою дифференциальным уравнением
Требование найти переходную функцию означает, что и решение
необходимо искать при нулевых начальных условиях.
Известно, что общее решение дифференциального уравнения имеет вид:
где - свободное движение системы, определяемое при отсутствии внешнего
55

Рис. 3.2.1.
56
воздействия, как решение уравнения при заданных начальных
условиях, - вынужденное движение системы, описываемое решением
неоднородного дифференциального уравнения
При нахождении переходной или весовой функций начальные условия должны быть
положены равными нулю.
11оэтому, здесь свободное движение отсутствует, т.е.
Для определения вычисляем корни характеристического уравнения
однородного дифференциального уравнения.
Общее решение однородного уравнения имеет вид:
Частное решение неоднородного уравнения имеет вид . В результате
подстановки в неоднородное уравнение имеем
Общее решение неоднородного дифференциального уравнения имеет вид:
Из начальных условий
можно получить
Тогда вынужденная составляющая движения системы описывается
Тогда аналитическое выражение для переходной функции динамического звена
имеет вид:
Аналитическое выражение для весовой функции определяется аналогичным
образом, полагая, что
[ рафики переходной и весовой функций приведены на рис.3.2.1.

3.3. Частотные характеристики
Частотные характеристики устанавливают связь между спектром
входного сигнала и спектром выходного сигнала . Комплексные
функции и представляют собой преобразование Фурье от
входного и выходного сигналов:
где - частота гармонического сигнала,
Комплексной частотной характеристикой принято называть функцию,
представляющую собой отношение спектра выходного сигнала к спектру
входного
Функция формально может быть получена из передаточной функции
В инженерной практике удобно пользоваться модулем и
аргументом комплексной частотной характеристики
- называется амплитудно-частотной характеристикой
(АЧХ) и отражает изменение амплитуды гармонических сигналов при
прохождении через систему в зависимости от частоты
- называется фазо-частотной характеристикой (ФЧХ) и
отражает изменение фаз гармонических сигналов при прохождении через
систему в зависимости от частоты
Комплексная частотная характеристика может быть выражена в
различных формах
*
где - вещественная часть комплексной функции ,
называемая вещественной частотной характеристикой (ВЧХ);
мнимая часть функции , называемая мнимой
частотной характеристикой (МЧХ).
Нетрудно установить, что между различными частотными
характеристиками существуют связи
57
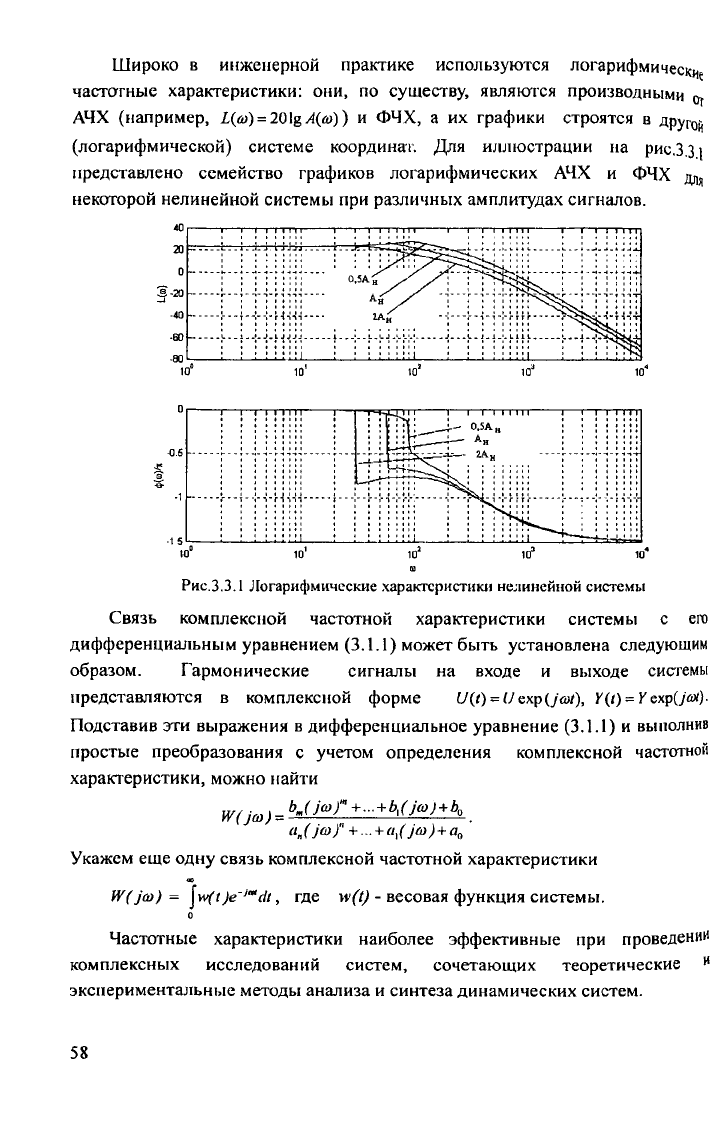
Широко в инженерной практике используются логарифмические
частогные характеристики: они, по существу, являются производными oj
АЧХ (например, ) и ФЧХ, а их графики строятся в дру^
(логарифмической) системе координат. Для иллюстрации на рис.3.31
представлено семейство графиков логарифмических АЧХ и ФЧХ д,,
некоторой нелинейной системы при различных амплитудах сигналов.
Рис.3.3.1 Логарифмические характеристики нелинейной системы
Связь комплексной частотной характеристики системы с его
дифференциальным уравнением (3.1.1) может быть установлена следующим
образом. Гармонические сигналы на входе и выходе системы
представляются в комплексной форме
Подставив эти выражения в дифференциальное уравнение (3.1.1) и выполнив
простые преобразования с учетом определения комплексной частотной
характеристики, можно найти
Укажем еще одну связь комплексной частотной характеристики
, где - весовая функция системы.
Частотные характеристики наиболее эффективные при проведении
комплексных исследований систем, сочетающих теоретические и
экспериментальные методы анализа и синтеза динамических систем.
58

3.4. Передаточные функции
Другой формой вход-выходного описания динамической системы
(элементов) является передаточная функция. Передаточная функция системы
определяется как отношение изображений по Лапласу выходного
и выходного сигналов при нулевых начальных условиях [8]
(3.4.1)
где - изображение по Лапласу от функции
- изображение по Лапласу от функции . О преобразовании
Лапласа - разд.3.4.1.
Введение передаточных функций позволяет решать задачи анализа и
синтеза динамических систем операторными методами.
Основным достоинством передаточных функций является возможность
достаточно легко и просто описать систему, когда известны передаточные
функции подсистем и схемы соединения подсистем друг с другом.
Так, существует три вида типовых
соединений подсистем друг с другом -
последовательное (рис.3.4.1а), параллельное
(рис.3.4.lb) и соединение с обратной связью
(встречно-параллельное) (рис.3.4.1 .с).
Возникают значительные трудности при
определении математической модели всего
соединения, когда математические модели
подсистем заданы в дифференциальной
форме.
При использовании моделей в форме
передаточных функций эта процедура
значительно облегчается и формализуется.
Так, для последовательного соединения
видно, что с учетом определения (3.4.1)
получается
. Тогда
Рис. 3.4.1. Типовые соединения
подсистем
59

Отсюда , . Таким
образом, последовательному соединению подсистем соответствует
умножение передаточных функций.
Рассуждая аналогично, можно получить, что параллельному соединению
подсистем соответствует сложение передаточных функций, т.е,
, встречно-параллельному соединению соответствует
соотношение для случая , и соотношение
для случая
Проведение арифметических операций над дробно-рациональными
полиномами (передаточными функциями) значительно проще, чем получение
аналогичного по сути результата при использовании дифференциальных
уравнений подсистем.
3.4.1. Преобразование Лапласа н его свойства
Сущность преобразования Лапласа заключается в том, что некоторой
функции действительной переменной ставится в соответствие другая
функция комплексной переменной при условии, что существует
(сходится) интегральное преобразование [9]:
(3.4.2)
- называется функцией-оригиналом (или просто оригиналом).
- называется функцией-изображением (или просто изображением).
Для того, чтобы функция являлась оригиналом и имела функцию
изображения необходимо и достаточно выполнение следующих условий:
1. функция непрерывна для всех , за исключением конечного
числа точек разрыва I рода,
2. функция для всех значений
3. функция имеет ограниченный порядок роста, т.е. можно указать
такие постоянные числа и для которых выполняется
условие при
Многие функции, встречающиеся при описании процессов в
динамических системах, являются оригиналами. Например, оригиналами
являются и ряд других, наличие в этих
функциях множителя - единичной ступенчатой функции - обеспечивает
60
