Асанов А.З. Моделирование и анализ динамических систем
Подождите немного. Документ загружается.


На практике пользуются двумя формами уравнений в относительных единицах.
13 первой форме, полученной нами выше, время не приводится к безразмерному
виду, и тогда при каждой производной, входящей в дифференциальное уравнение, стоит
коэффициент, имеющий размерность времени в степени, равной порядку производной:
при первой производной коэффициент имеет размерность сек, при второй производной -—
сек2, при третьей - сек3 и т. д.
Во второй форме время, как и все другие переменные, приводят к безразмерному
виду. Для этого его относят к некоторой постоянной времени, чаще всего к времени Т, или
так называемой постоянной времени звена.
2.4.4. Особенности формирования математических моделей
экономических систем.
Рассмотрим наиболее существенные характеристики экономических
систем как объектов управления [5].
Экономическая система, охватывая параметры и характеристики
производства, распределения, обмена и потребления материальных благ,
является подсистемой социально-экономической суперсистемы, т. е. цели ее
функционирования подчинены социальным целям и вытекают из них.
Любая экономическая система зависит от множества факторов и
осуществляет совокупность функций, реализует множество целей. Это
означает, что в процессе функционирования, например, предприятия,
одновременно ставятся цели:
• добиться максимально возможной прибыли от выпуска продукции,
• обеспечить высокий уровень сервиса,
• снизить себестоимость,
. обеспечить определенный уровень качества и рентабельности
производимой продукции.
Некоторые из этих показателей по своей направленности могут быть
противоречивыми: например, стремление обеспечить высокий уровень
сервиса одновременно ведет и к суммарному росту себестоимости.
Экономические управленческие задачи плохо структурированы и не
всегда модель может быть построена однозначным образом.
Итеративный режим использования в экономике математических
моделей - один из характерных приемов при моделировании плохо
структурированных задач. Процесс сходимости искомых показателей в
итеративном режиме понимается как целенаправленный человеко-машинный
диалог с возможными изменениями исходных данных и, если необходимо,
41

отдельных элементов модели, т.е. происходит уточнение (самообучение)
самой модели экономического объекта с помощью имитации еГ(]
функционирования.
Экономика - сложная иерархическая динамическая система.
В зависимости от цели исследования экономику представляют 8
различных разрезах. Так, на верхнем уровне иерархии экономит
рассматривают как систему общественного производства, распределения
обмена и потребления. Такое разбиение удобно для исследовании
общественных отношений, складывающихся в процессе производства.
Однопродуктовая динамическая макроэкономическая модель
Исследование взаимосвязей элементов производства вне общественной
формы приводит к рассмотрению производственно-технологической
интерпретации экономики.
Производство может быть охарактеризовано взаимодействием и
взаимосвязями (рис.2.4.6) следующих основных факторов: трудовых
ресурсов (L), средств труда - основных производственных фондов (К) и
предметов труда (W).
Предметы труда включают, с одной стороны, природные ресурсы ( ) и
собственно предметы труда (W), возвращенные в производство как часть
совокупного общественного продукта.
Валовой продукт (А), произведенный в результате производственной
деятельности, идет на производственное потребление (If') и выделяется в
качестве конечного продукта (Y), т.е.
В свою очередь, конечный продукт ( У) делится на валовые капитальные
вложения (/) и непроизводственное потребление ((7), т.е.
Валовые капитальные вложения (Г) делятся на амортизационные
отчисления (Л) и чистые капитальные вложения ( /с), идущие на расширение
производственных фондов.
Механизм воздействия чистых капитальных вложений на основные
производственные фонды (ОГГФ) сложен и при моделировании связан с
определенными трудностями. Он составляет предмет самостоятельных
экономико-математических исследований.
Рассмотрим взаимосвязи между показателями верхнего уровня
экономической иерархии. Одним из подходов к решению данной п р о б л ем ы
является построение так называемой однопродуктовой м а к р о э к о н о м и ч е с к о й
модели.
42
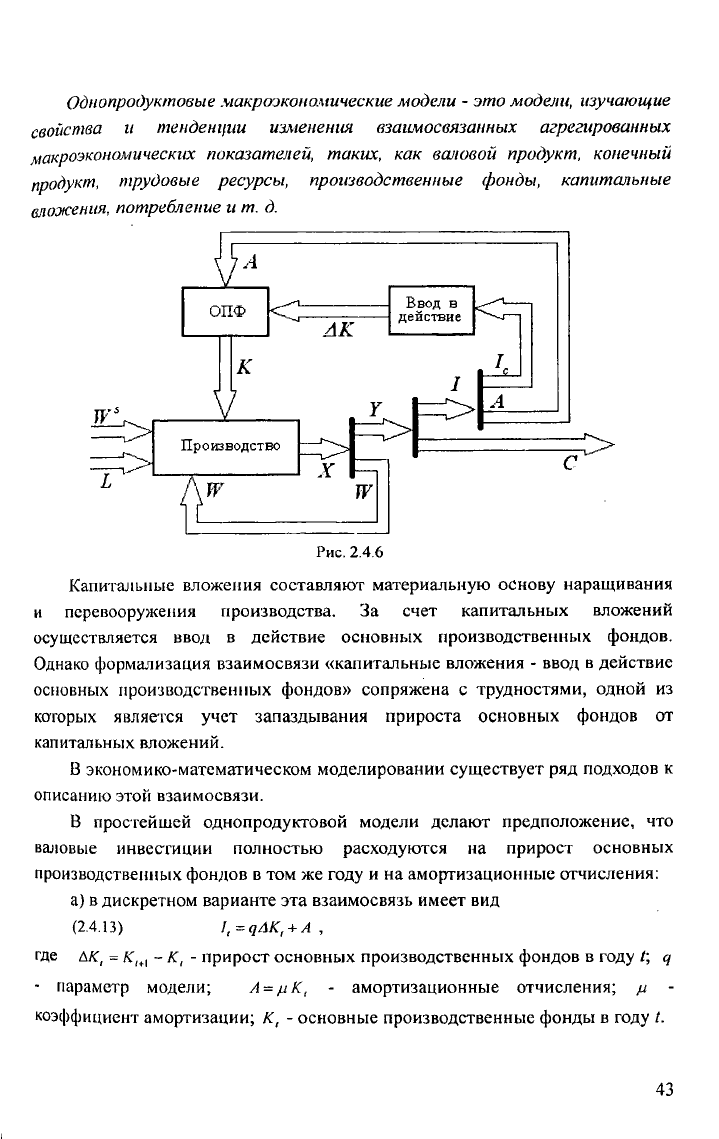
Однопродуктовые макроэкономические модели - это модели, изучающие
свойства и тенденции изменения взаимосвязанных агрегированных
макроэкономических показателей, таких, как валовой продукт, конечный
продукт, трудовые ресурсы, производственные фонды, капитальные
вложения, потребление и т. д.
Рис. 2.4.6
Капитальные вложения составляют материальную основу наращивания
и перевооружения производства. За счет капитальных вложений
осуществляется ввод в действие основных производственных фондов.
Однако формализация взаимосвязи «капитальные вложения - ввод в действие
основных производственных фондов» сопряжена с трудностями, одной из
которых является учет запаздывания прироста основных фондов от
капитальных вложений.
В экономико-математическом моделировании существует ряд подходов к
описанию этой взаимосвязи.
В простейшей однопродуктовой модели делают предположение, что
валовые инвестиции полностью расходуются на прирост основных
производственных фондов в том же году и на амортизационные отчисления:
а) в дискретном варианте эта взаимосвязь имеет вид
(2.4.13)
где - прирост основных производственных фондов в году ;
- параметр модели; - амортизационные отчисления;
коэффициент амортизации; - основные производственные фонды в году .
43

б) Аналогом последнего уравнения в непрерывном варианте является
Отсюда можно получить уравнение движения фондов
Учитывая , и (2.4.13), получим однопродуктовую
динамическую микромодель в дискретном варианте:
Если считать производственные затраты W пропорциональными
выпуску продукции X, т. е. , то дискретная однопродуктовая
динамическая модель примет вид:
или ,
а в непрерывном варианте - соответственно
(2.4.14)
В некоторых случаях используют упрощенные варианты
однопродуктовой динамической модели.
Так, можно положить, что все капитальные вложения идут на ввод в
действие новых основных производственных фондов и при этом основные
фонды не изнашиваются. Считая, что прирост выпуска продукции
, пропорционален капитальным вложениям, т. е. ,
можно получить модель вида
которая носит название однопродуктовой открытой динамической модели
Леонтьева.
В непрерывном варианте однопродуктовая динамическая макромодель
Леонтьева имеет вид
С математической точки зрения эта модель представляет собой линейное
неоднородное дифференциальное уравнение.
В другом варианте можно положить, что непроизводственное
потребление идет полностью на восстановление рабочей силы
Тогда, введя норму потребления , получим
Далее, если считать, что затраты труда пропорциональны выпуску
продукции, то , где - норма трудоемкости.
С учетом (2.4.14) и последних соотношений, можно получить
44

«замкнутую по потреблению» модель расширенного воспроизводства
(замкнутая однопродуктовая модель Леонтьева):
Последнее уравнение является однородным дифференциальным уравнением
вида
(2.4.15) , где
Тогда развитие экономики определяется решением этого уравнения:
Можно рассмотреть случай, когда непроизводственное потребление
является известной функцией времени.
В этом случае закон развития экономики можно определить из модели
(2.4.15), которая с математической точки зрения является неоднородным
дифференциальным уравнением вида
, где , с решением
Таким образом, можно сделать следующий вывод.
Выделение из конечного продукта У накапливаемой части I приводит к
рассмотрению динамических моделей и применению для исследования в
качестве математического аппарата теории дифференциальных (в непрерыв
ном случае) и конечно-разностных уравнений (в дискретном варианте).
2.5. Способы отображения структур динамических систем
Методы отображения структур систем (топологические методы)
позволяют получать графическое изображение динамических систем,
сигналов и их внутренних связей. Понятие передаточной функции позволяет
построить удобные графические представления математических моделей
линейных систем, которые сами могут рассматриваться как изобразительные
модели, эквивалентные аналитическим моделям. Чаще всего используются
Два вида графических моделей - структурные схемы и графы.
45

2.5.1. Структурные схемы
Структурной схемой принято называть условное графическое
изображение структуры динамической системы (или сложного элемента)
При этом под структурой понимается совокупность частей, на которые
система разделяется по тем или иным признакам, и связей, изображающей
каналы, по которым передается воздействие от одной части к другой [6].
На структурную схему наносятся условными знаками (рис. 2.5.1) все
динамические звенья, внешние воздействия и воздействия элементов друг на
друга.
Рис. 2.5.1. Условные знаки структурных схем
Динамическое звено изображается прямоугольником, в котором указы
вается передаточная функция этого звена. Воздействия на систему и
воздействия элементов (звеньев) друг на друга изображаются стрелками.
Около каждой стрелки указывается, какую физическую величину или
обобщенную координату системы она изображает. Изменения этой величины
и являются сигналом, передаваемой информацией. На динамическое звено
может воздействовать лишь одна входная величина, поэтому используются
знаки суммирования и сравнения сигналов. Суммироваться и сравниваться
могут лишь сигналы одной и той же физической природы. В каждом
динамическом звене воздействие передается только от входа к выходу.
Структурная схема показывает строение системы, наличие внешних
воздействий и точки их приложения, пути распространения воздействий и
выходную величину. По структурной схеме можно составить математическое
описание исследуемой системы, т. е. систему алгебраических у р а в н е н и й
относительно изображений всех переменных (обобщенных координат) или ее
46
входная ш и выходная величина (воздействие, сигнал)
динамическое звено (подсистема) с передаточной функцией
разветвление сигнала
суммирование сигналов
вычитание (сравнение) двух сигналов
инвертирование (изменение знака) сигнала

передаточные функции.
Для составления структурной схемы динамической системы необходимо
иметь ее функциональную схему, которая содержит сведения о назначении
элементов, о роли внешних воздействий и о регулируемой величине. Кроме
того, необходимо иметь дифференциальные уравнения всех элементов для
определения их передаточных функций или же иметь экспериментально
найденные передаточные функции.
При составлении структурной схемы удобно начинать с изображения
задающего воздействия и располагать динамические звенья, составляющие
прямую цепь системы, слева направо до регулируемой величины. Тогда
основная обратная связь и местные обратные связи будут направлены справа
налево.
В настоящее время существует достаточно большое число различных
модификаций в условных обозначениях и правилах формирования
структурных схем. Так, для обозначения векторных величин (сигналов) часто
используются спаренные линии (стрелки). Например, для иллюстрации
системы матричных уравнений вида
где X.Y.U - вектора, а - матрицы соответствующих размеров,
используется структурная схема такой
модели на рис.2.5.2. Эта схема
показывает взаимодействие различных
векторов сигналов друг с другом,
показывает преобразование тех или
иных сигналов блоках-матрицах.
Здесь, кроме того, подразумевается
наличие начальных условий координат
С учетом, что центральная
часть структурной схемы
неизменна всегда и требуется в
явном виде показать наличие
начальных условий , эта
структурная схема может быть еще
более упрощена и представлена в виде, как на рис. 2.5.3.
Две последние структурные схемы полностью идентичны друг другу.
47
Рис 2.5.3 Структурная схема модели
Рис. 2.5.2. Структурная схема модели

Следует заметить, что структурные схемы можно рассматривать как
один из видов направленного графа.
2.5.2. Направленные графы
Направленный граф (сигнальный граф, диаграмма прохождения сигнала)
представляет собой совокупность узлов (вершин) и соединяющих их ветвей
(дуг) с обозначением направления передачи сигналов и их пропускной
способности. Если рассматривать структурную схему как граф, то обычно
узлами (вершинами) считают все переменные величины (воздействия,
сигналы), а ветвями (дугами) — динамические звенья, тогда передаточные
функции определяют их пропускную способность.
Направленным графом принято называть совокупность направленных
ветвей, соединенных в ряде точек, называемых вершинами, которая
однозначно определяет систему линейных алгебраических уравнений.
Различают три основных вида направленных графов [7]:
сигнально-потоковые графы (графы Мезона),
потоковые графы (графы Коутса),
./^-деревья.
Первые два из них особенно пригодны для электрических систем - они
исходят из рассмотрения определяющих уравнений системы. Метод К-
деревьев лучше всего применим, когда интересуются физической структурой
системы.
Сигнально-потоковые графы лучше всего использовать, если система
имеет только один вход. Они дают хорошую физическую картину работы
системы, так как раскрывают причинно-следственные связи между
сигналами на всех стадиях, когда производится процедура сведения к графу.
Потоковые графы, которые является модификацией сигнально
потоковых графов, можно применять к системе, которая имеет несколько
входов, но не может быть расчленена с помощью простой техники сведения к
графу.
Главной особенностью использования К-деревьев является то, что в нем
не используется многочисленные понятия, как в и первых двух методах, и.
таким образом, этот подход упрощает расчеты.
Здесь будут рассмотрены только сигнально-потоковые графы (графы
Мезона), т.к. они чаще всего используются при исследованиях динамических
систем.
48

Сигнально-потоковые графы. Сигнально-потоковый граф - это
графическое представление набора независимых линейных отношений
системы [7].
Каждый граф состоит из точек соединения, называемых узлами, которые
связаны между собой некоторым числом направленных линейных отрезков -
дуг графа. Узлы изображают сигналы или переменные величины системы.
Дуга - это направленный отрезок линии со стрелкой, определяющей
направление сигнала. Стрелки показывают, как связаны между собой вход и
выход. Если в некоторую вершину графа входит несколько ветвей, то она
обозначает сумму соответствующих сигналов.
Основные понятия для сигнально-потокового графа следующие
(иллюстрации - на рис.2.5.2).
Источник. Узел, в который не входит ни одна дуга (узел ).
Сток. Узел, из которого не выходит ни одна дуга (узел ).
Промежуточный узел. Узел, имеющий как
входящие в него, так и выходящие из него дуги
(узлы ).
Открытый путь. Любой путь, вдоль кото
рой каждый узел может встретиться только один
раз (abed или aeh).
Прямой путь. Открытый путь между источ
ником и стоком (abcd или aehd, но не aef).
Контур обратной связи. Путь, начинающийся и кончающийся в одном и
том же узле, вдоль которого ни один узел, за исключением начального, не
встречается дважды (контур g и ef, но не egf).
Петля. Контур обратной связи, состоящий из единственной дуги (g, но
не ef).
Коэффициент (обобщенный) усиления дуги. Линейная величина,
соотносящая одни узел другому независимо от их размерностей (а, b, с, d, е, f,
g, h).
Коэффициент (обобщенный) усиления контура. Произведение
коэффициентов усиления дуг замкнутого контура (е умножить на f).
Простейшие примеры графов приведены на рис.2.5.3, где показаны
сигнальные графы для усилителя с коэффициентов усиления к, для
интеграторов, для апериодического звена с передаточной функцией
49
Рис.2.5.2. Пример графа

Рис.2.5.3. Примеры сигнальных графов:
а) граф усилителя; б) граф интегратора (1 вариант);
в) граф интегратора (2 вариант), г) граф апериодического звена
Графы интеграторов на рис.2.5.3 принципиально друг от друга не
отличаются, хотя второй вариант предпочтителен из-за наглядности и
краткости.
Примером использования таких обозначений служит граф схемы
моделирования электродвигателя постоянного тока, на сумматорах и
интеграторах, приведенный на рис.2.5.4.
Важным достоинством сигнальных графов, обусловивших их широкое
распространение, является возможность находить передаточные функции
системы непосредственно по графу, минуя этап выписывания уравнений
отдельных блоков и исключения промежуточных переменных. Это делается с
помощью правила Мезона, которое состоит в следующем.
Пусть дан сигнальный граф линейной динамической системы и требуется
найти передаточную функцию (обобщенный коэффициент передачи) от
его входной вершины (истока) до выходной вершины (стока). Согласно
правилу Мезона искомая передаточная функция вычисляется по формуле
где - коэффициент передачи -го прямого пути от источника к стоку;
- определитель графа;
- сумма коэффициентов передачи всех контуров обратной связи;
- сумма попарных произведений коэффициентов передачи для
всевозможных комбинаций из двух несоприкасающихся контуров;
сумма произведений коэффициентов передачи ДлЯ
Рис.2.5.4 Граф модели
электродвигателя постоянного тока
