Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Solutions of exercises 327

 Solution of exercise 11.6. Using the technique described in the text on page 310, we ﬁrst

compute that

−a|x|

∗sin b |x| =

2 b

+ b

−a|x|

+ b

sin b |x|,

and using the formula of exercise 8.13 on page 243 we get

S =

2a(a

+ b

)

coth a +

2 b (a

+ b

)

sin b

1 −cos b

 Solution of exercise 11.7

i) A simple change of variable and the periodicity of the co sine function imply t hat the

integral does not depend on α ∈ R. Moreover, putting α = π/2, a si ne appears, and as

this is an odd function, it follows that the integral is real.

ii) Passing in polar coordinates (x, y) 7→ (r,θ), we get

f (u, v) = ψ(ρ) =

2iπ(ux+ v y)

dx dy

+∞

ϕ(r)

Z

−π

2iπρr cosθ

dθ



r dr,

ψ(ρ) = 2π

+∞

r ϕ(r) J

(2πρr) dr.

This will be denoted, as indicated, by ϕ(r)

H. T.

−−→ ψ(ρ).

iii) This is simply the translation of the Fourier inversion formula in this context.

iv) In the formula

dϕ

we recognize the expression for the laplacian of f in polar coordinates, since there is

no dependency on θ. The Fourier t ransform of △f is equal to −4π

f (u, v) with

ρ = (u, v) and ρ

= ρ

, hence the formula follows.

v) The Parseval-Plancherel identity

(x, y) f

(x, y) dx dy =

(u, v)

(u, v) du dv,

gives, in polar coordinates, the required identity:

2π

∞

r ϕ

(r) ϕ

(r) dr = 2π

∞

ρ ψ

(ρ) ψ

(ρ) dρ.

 Solution of exercise 11.9. As seen on page 320, th e amplitude of the diffraction ﬁgure is

given radially by the Hankel transform of th e radial transmittance function, whi ch is given here

f (x, y) = f (r) =

0 if r > ℓ,

1 if r < ℓ,

where r =

+ y

The amplitude is therefore

A(θ, ϕ) = A(ρ) =

ℓ

(2πρℓ) with ρ =

+ ϕ

328 Fourier transform of distributions

−

Fig. 11.7 — The diffraction ﬁgure created by two circular holes. The spacing between the

two lenses is here taken to be 4 times their diameter.

The transmittance function of two holes is

g(x, y) = f (x, y) ∗



x −



+ δ



x +

i

The diffraction ﬁgure due to the two holes is obtained by multiplying the diffraction amplitude

due to a single hole by the Fourier transform of the distribution δ (x −a/2) + δ (x + a/2),

which is equal to 2 cos(πθa).

We obtain then the result sketched in Figure 11.7.

 Solution of problem 5. The total density of charge is

q( r) =

( r) + q

δ( r ).

Denote by ϕ( r) the effective el ectrostatic potential created by the distribution of charge q( r)

(including therefore both the exterior charge and the induced polarizat ion cloud). The quan-

tities ϕ( r) and q( r ) are related by two equations. The ﬁrst, an electrostatic relation, is th e

Poisson equation, which is

△ϕ( r ) = −4π q( r ) ; (∗)

in Gauss units. The second, a thermodynamic relation, is the Boltzmann equation

( r) = ρ

−βe

ϕ( r )

, (∗∗)

where the constant value of ρ

is justifed by the fact that, for r → ∞, we have ϕ( r) → 0 in

the suitable gauge and ρ

( r) → ρ

In th e limit of weak couplings (or low densities), we can l inearize equation (∗∗) and obtain

( r) = ρ



1 −βe

ϕ( r )



which, inserted into (∗), gives

(△−κ

) ϕ( r) = −4πq

δ( r ) with κ

def

= 4πβ

linearized Poisson-Boltzmann

taking into account that the system is neutral (

= 0).

Solutions of exercises 329

We will now try to solve this equation. First, assuming that ϕ( r) has a Fourier transform,

we obtain the conjugate equation

(−k

−κ

) eϕ( k) = −4πq

with the conventions

eϕ( k)

def

−i k·r

ϕ( r ) d

r and ϕ( r) =

(2π)

i k·r

eϕ( k) d

We deduce that

eϕ( k) =

4πq

+ κ

There only remains to compute the inverse Fourier transform

ϕ( r ) =

4πq

+ κ

i k·r

(2π)

For t his purpose, we u se spheric al coordinates on the space of vectors k, with the p ol ar

axis oriented in the direction of r, and with the notation k · r = kr cos θ, where k > 0 and

r > 0. Then

ϕ( r ) =

2π

dϕ

dθ

+∞

4πq

+ κ

sin θ e

ikr cosθ

(2π)

ϕ( r ) =

−1

d(cos θ)

+∞

8π

+ κ

ikr cos θ

(2π)

+∞

+ κ

ikr



ikr

−e

−ikr



dk =

2 q

πr

+∞

k sin kr

+ κ

dk.

We must still evaluate this integral relative to the variable k. For this, we put

I ( r)

def

+∞

k sin kr

+ κ

dk =

Z

+∞

−∞

k e

ikr

+ κ



and we use the method of residues by extending the variable k to the complex plane. The poles

of the meromorphic function f (z)

def

= z e

i zr

/(z

+ κ

) are located at z

= iκ and z

= −iκ.

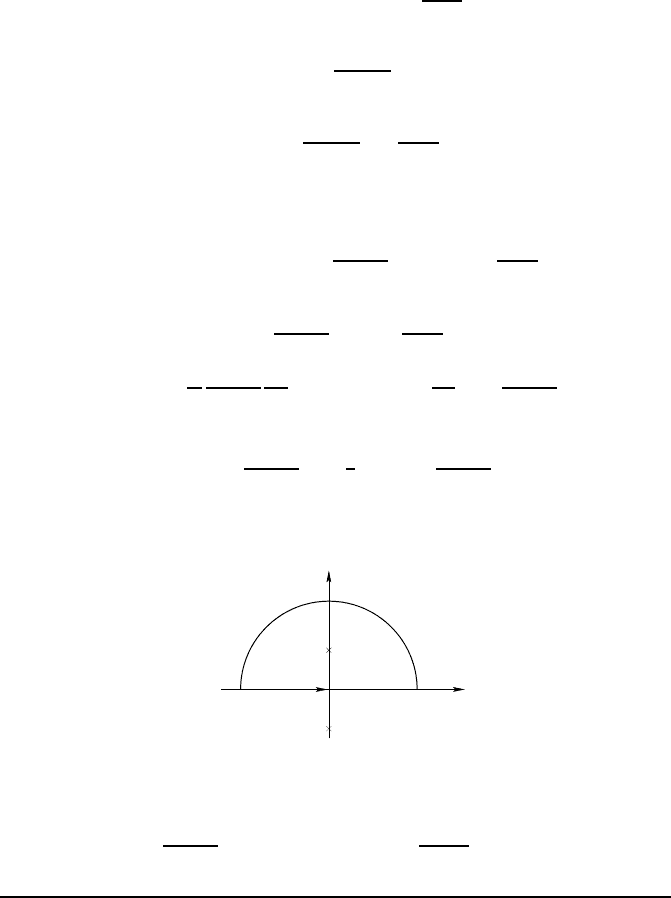
Since r > 0, we can integrate on the co ntour described in the following ﬁgure:

and, after applying Jordan’s second lemma 4.85, as justiﬁed by the fact that k/(k

+ κ

) tends

to 0 when [k → ∞], and after taking the limit where the radius in the contour goes to inﬁnity,

we derive

+∞

−∞

k e

ikr

+ κ

dk = 2iπ Res ( f ; z

) = 2iπ

ik e

−κr

2iκ

= iπ e

−κr

Being careful of the fact that, in the general case, the equation x T (x) = a has solutions

given T (x) = a pv(1/x) + bδ, with b ∈ C. Here, eϕ( k) is deﬁned up to th e addition of the

Fourier transform of an harmonic functions.

330 Fourier transform of distributions

hence I =

−κr

and ϕ( r) =

−κr

Debye potential.

Using the Boltzmann e quation, each of the functions ρ

( r) can be computed now. Note

that the Debye electrostatic screen occurs at a length scale of κ

−1

, which tends to inﬁnity in the

limit of weak coup lings (small densities). For distances r ≪ κ, the potential is ϕ( r) ≈ q

/r,

and we recover the Coulomb potential.

The total charge present around q

Q =

ZZZ

( r ) d

ZZZ



1 −βe

ϕ( r )



= −

ZZZ

βe

ϕ( r ) d

r by initial neutrality,

= −q

ZZZ

βρ

−κr

r = −q

Thus is exactly compensates the additional charge q

. In other words, the system has managed

to become neutral again.

The De bye screen is said to be a total screen.

This may seem surprising; whichever charge is added to the system, it remains neutral.

This is a strange property of an inﬁnite system, which may bring in charges from inﬁnity, and

make them disappear there. This type of paradox also happens in the famous “inﬁnite hotels,”

all rooms of which are occupi ed, but in which, ne vertheless, a new customer can always be

accommodated: it sufﬁces th at the person in Room 1 move to Room 2, the person in Room 2

move to Room 3, and more generally, the person in Room n move to Room n+1. All previous

occupants have a new room, and Room 1 becomes available for the new customer.

Chapter

The Laplace transform

The Laplace transform is an integral transformation, which is a kind of generaliza-

tion of the Fourier transform. It has a double interest:

1. it avoids using distributions in some cases where a function does not have a

Fourier transform in the sense of functions;

2. it can be used to solve problems described by differential equations taking

initial conditions into account, t h at is, it can attack t he Cauchy problem

associated to the system. An example will be given to the dynamics of the

electromagnetic ﬁeld without sources.

12.1

Deﬁnition and integrability

In t his chapter, we are interested in an integral transformation operating

on functions f which vanish for negative values of the var iable: f (t) = 0

for all t < 0 (no continuity at 0 is imposed). An example is the function

t 7→ H (t) cos t.

In the literature about the Laplace transform, the factor H (t) is frequently

omitted; we will follow this custom, except where some ambiguity may result,

and we will therefore speak of the function t 7→ cos t, tacitly assuming that

this deﬁnition is restricted to positive values of t.

DEFINITION 12.1 A causal fu nction is a function t 7→ f (t) deﬁned on R

which is zero for negative values of it s argument:

f (t) = 0 for any t < 0.

332 The Laplace transform

12.1.a Deﬁniti on

DEFINITION 12.2 Let f (t) be a real- or complex-valued locally integrable

function deﬁned for real values of t. The (unilateral) Laplace transform

of f ( t) is the complex function of the complex variable p denoted

f (p) (or

F (p)) which is deﬁned by

f (p)

def

+∞

f (t) e

−p t

dt.

Whereas the function

f it self is called t he Laplace tranform, the operation

f 7→

f should be called th e Laplace transformation.

DEFINITION 12.3 Let f be a locally integrable function on R. The bilateral

Laplace transform of f is the function

p 7−→

+∞

−∞

f (t) e

−p t

dt.

Its properties are of the same kind as those of the unilateral transform, wit h

variants that the reader may easily derive by herself.

The bilateral Laplace transform of H (t) f (t) is simply the Laplace trans-

form of the function f (t). In the remainder of this chapter, only the unilateral

transform will be considered.

Remark 12.4 If f is a function zero for t < 0 which has a Fourier transform, t h en the relation

f (iω) =



2π



with ω ∈ R

holds. The Laplace transform is an extension of the notion of Fourier transform. More

precisely,

f (x + iω) is, up to the change of variable ω = 2πν, the Fourier transform of t 7→

f (t) e

−x t

evaluated at ω/2π.

Sometimes th e following deﬁnition is found in the literature:

DEFINITION 12.5 (Original, image) An original is any function of a real

variable which is locally integrable, with real or complex values, such that

i) f is causal ( f (t) = 0 for a ll t < 0);

ii)



f (t)



does not increase faster than any exponential function, that is,

there exist constants M > 0 a nd s ∈ R such that



f (t)



¶ M e

for all t ∈ R.

The Laplace transform of an original is the image of the original.

Deﬁnition and integrability 333

Pierre Simon, marquis de Laplace (1749—1827), befriended

d’Alembert (p. 415) at eighteen, found a positi o n as professor

of mathematics at the Paris military school, and then became a

professor at the École Polytechnique. He was passionate about

astronomy and developed many concepts and useful tools for

the study of mechanics, in particular in the ﬁeld of differential

equations. He studied cosmology and cosmogony (the prim-

itive nebula of Laplace), rediscovered the forgotten works of

Bayes (p. 518) and was the ﬁrst to compute the integral of the

gaussian. When Napoléon asked why he did not mention God

in his Traité de mécanique céleste, his answer was: “Je n’ai pas eu

besoin de cette hypothèse” (I did not need this assumption).

The following notation are used: if f (t) is an original, its Laplace trans-

form is denoted

f (p) or F (p). The symbol ⊐ is also in w idespread use, used

as follows: f (t) ⊐ F (p). (In certain russian books, th e notation f (t) º F (p)

also appears.)

12.1.b Inte grability

In the remainder of this chapter, we write p = x + iω.

Let f be a locally integrable function. We are looking for the domain

where its Laplace transform

f (p) is deﬁned. Note ﬁrst that integrability of

t 7→ f (t) e

−p t

is equivalent to integrability of t 7→ f (t) e

−x t

Moreover, if this function is integrable for some x

, then it is also inte-

grable for any x > x

, since



f (t) e

−x t



f (t) e

−x



−x)t



f (t) e

−x



It follows that th e set of complex numbers p, where t 7→ f (t) e

−p t

is in-

tegrable, either is empty or is a (right) half-plane in the complex plane, or

indeed is the entire complex plane C.

DEFINITION 12.6 The convergence a bscissa of the original function f is the

lower bound of all real numbers x for which the function above is integrable:

def

= inf

x ∈ R ; t 7→



f (t)



−x t

is integrab le

From the previous reasoning, we deduce th e following result:

PROPOSITION 12.7 Let f (t) be an original and let α be its convergence abscissa.

Denote as before p = x + iω. Then

i) for x < α, the function t 7→ f (t) e

−p t

, is not integrable;

ii) for x > α, this fu nction is integrable;

334 The Laplace transform

iii) for x = α, it may, or may not, be Lebesgue-integrable. If it is not Lebesgue-

integrable, the improper integral

+∞

−∞

f (t) e

−p t

dt = lim

R→+∞

′

→−∞

′

f (t) e

−p t

may still converge for certain values of p = α+iω, wh ich provides an extension

of the Laplace transform of f to those values of p.

Example 12.8 Consider the Heaviside function. Its Laplace transform is given by

H (p) =

+∞

H (t) e

−pt

dt =



−pt



+∞

so that the convergence abscissa of H is e qual to 0, and for all p ∈ C such that Re(p) > 0, we

have

H (p) = 1/p. The domain where

H is deﬁned is thus an open half-plane.

Notice that, if the function

H is extended to the imaginary axis (except the origin) by

deﬁning, for any nonzero ω, H (iω) = 1/iω, we obtain a function which is “close” to the

Fourier transform of H , the latter being equal to

H (ν) = pv

2iπν

which is the same as pv(1/2iπν) on R

∗

. This resemblance will be explai ned in Section 12.4.e,

page 345.

Example 12.9 Let f (t) = 1/(1 + t

). Then we have

F (p) =

+∞

−pt

1 + t

dt,

which is deﬁned for all p ∈ C such that Re(p) ¾ 0. The domain of deﬁnition o f F is therefore

a closed half-plane.

Example 12.10 Let a ∈ C be an arbitrary complex number, and consider the Laplace transform

of the function t 7→ H (t) e

. We have

H (t) e

⊐

+∞

−pt

dt =

+∞

−( p−a)t

dt,

so that the convergence abscissa is α = Re(a), and for all p ∈ C such that Re(p) > Re(a), the

Laplace transform of H (t) e

is 1/(p − a).

THEOREM 12.11 In the open half-plane on the right of the abcissa of convergence,

the Laplace transform

f is holomorphic and hence also analytic.

Proof. Let x ∈ R with x > α. Then, for any m ∈ N, the function t 7→ t

f (t)e

−pt

integrable: since x > α, t h e real number y = (x + α)/2 satisﬁes α < y < x; moreover,

t 7→ f (t) e

−yt

is integrable, and we may write



f (t)



−x t



f (t)



−yt

· t

−(x−a)t/2

where the ﬁrst factor is integrable whi l e the second is bounded. The derivative of F

can be computed using the theorem of differentiation under the integral sig n, and is

given by

= F

′

(p) =

∞

(−t) f (t) e

−pt

dt.

Deﬁnition and integrability 335

iω

α=−∞

←−−−

iω

α < 0

(a) (b)

iω

α = 0

iω

α > 0

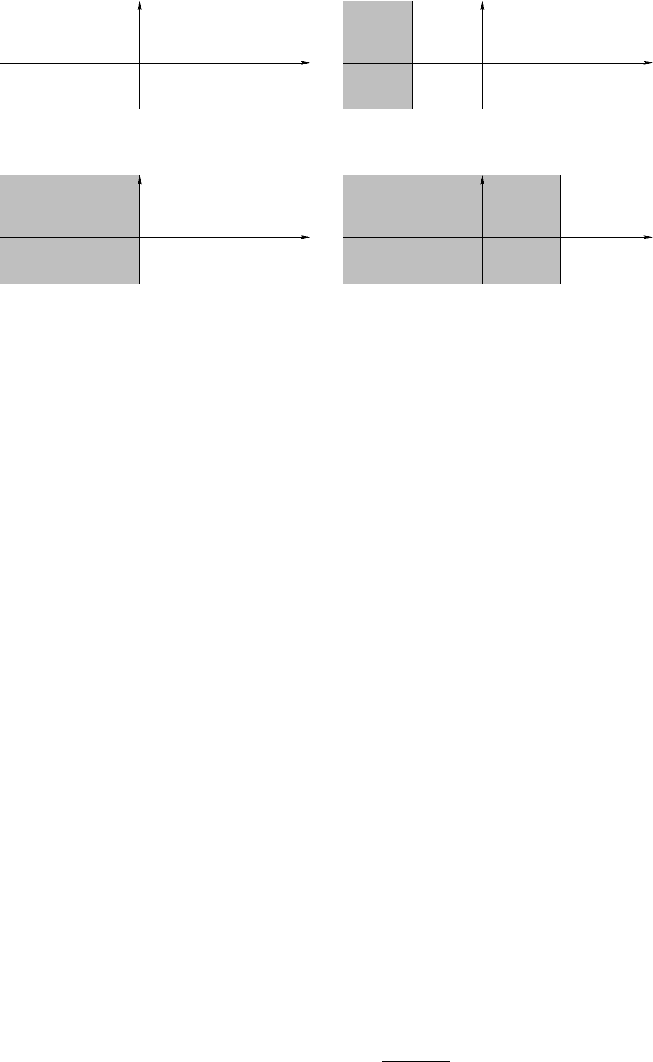
Fig. 12.1 — Convergence abcissas for unilateral Laplace transforms. (a) Function wit h

bounded support on the rig h t. (b) Function rapidly decaying on the right.

set, the Laplace transform is holomorphic.

Since F is differentiable in the complex sense at any point of t h e op en half-plane

{p ∈ C ; Re p > α}, it is an analytic function.

Notice that the convergence abcissa for t 7→ t f (t) is the same as that for f . Also,

an obvious induction shows that

(n)

(p) =

∞

(−t

) f (t) e

−pt

dt.

We will admit the following result, which is summarized in Figure 12.1:

PROPOSITION 12.12 Let f be an original.

i) If the function f (t) has bounded su pport on the r ight, then α = −∞.

ii) If f (t) decays rapidly on the right, then −∞ ¶ α < 0 and

f (p) is holomor-

phic in a half-plane containing the imaginary axis (in particular, the Fourier

transform of f exists).

iii) If f (t) is tempered (in the sense of distributions) and does not tend to 0 at

inﬁnity, then α = 0; its Fourier transform does not necessarily exist in the sense

of functions, but it exists in the sens of distributions.

iv) Finally, if f (t) increases rapidly at inﬁnity, then 0 < α ¶ +∞; then

f (if

it exists) is holomorphic on a half-plane not containing the imaginar y axis and

the Fourier transform of f does not exist.

Example 12.13 The convergence abcissa for the “rectangle” function is −∞ and we have

Π(p) =

1/2

−pt

dt =

1 −e

−p/2

336 The Laplace transform

which is analytic on C; the singularity at 0 is indeed an arti ﬁc ial one, since

Π is bounded in a

neighborhood of 0;

Π h as the power series expansion

Π(p) =

∞

n=0



(−1)

n+1

(n + 1)! 2

n+1



Any nonzero po lynomial function or rational function has convergence abcissa equal to 0.

 Exercise 12.1 Show that the function g : t 7→ e

does not have a Laplace transform (that

is, α = +∞).

12.1.c P roperties of the Laplace transform

PROPOSITION 12.14 Let f (t) be an original and F(p) its image by the Laplace

transform. For x > α, the f unction F (x + iω) tends to 0 as ω → ±∞.

Proof. This is an easy consequence of the Riemann-Lebesgue lemma (see page 282):

lim

ω→±∞

+∞



f (t) e

−x t



−iωt

dt = 0.

We know that, on the right of the absciss a of convergence, the Laplace

transform is holomorphic. What happens elsewhere?

Take, for instance, f (t) = e

. The convergence ab scissa is α = 3. Its

Laplace transform is F (p) = 1/(p − 3) which is holomorphic everywhere

except at p = 3. More precisely, F is deﬁned in the convergence half-plane

{z ∈ C ; Re(z) > 3}, but it can be analytically c ontinued to the plane with

the single point {3} removed, namely, to C \ {3}. It often h appens that the

Laplace transform of an original is a meromorphic f unction.

Thus we will sh ow

that

cos t ⊐

+ 1

;

this image function is meromorphic and has poles at p = ±i. It is represented

in Figure 12.2, together with its analytic continuation to C \{−i, i}.

12.2

Inversion

It is possible to ﬁnd an inversion formula for the Laplace transform using

our knowledge of the Fourier inversion formula. Indeed, if F (p) is the Laplace

transform of the function f (t), we have, for any x > α,

F (x + 2iπν) =

+∞

−∞

H (t) f (t) e

−x t

−2iπνt

dt,

This is not always the case. It may have branch points, as in the case of the Laplace

transform of t 7→ H (t)/(t + 1).