Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Application to physical optics 317

-1,5 -1

-0,5 0,5

1 1,5

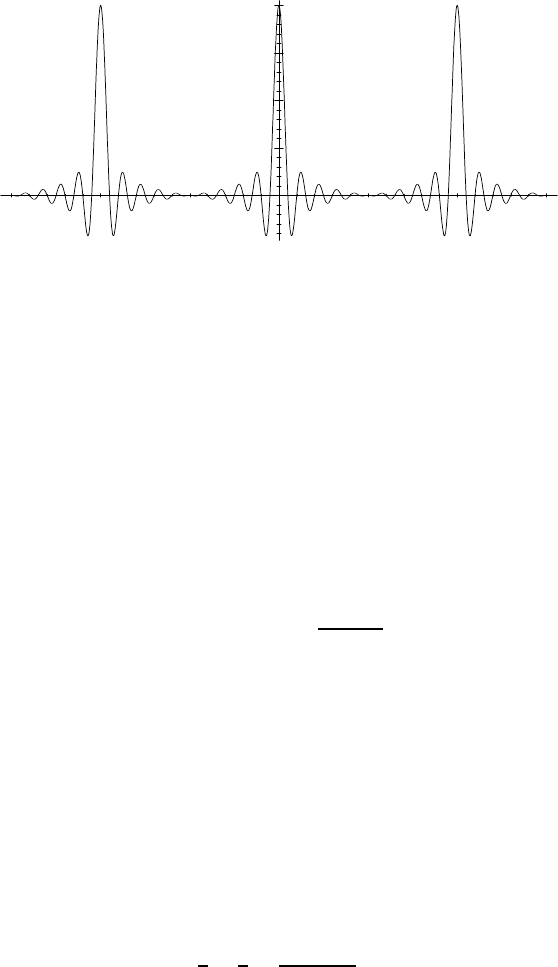
Fig. 11.2 — Intensity of the diffraction ﬁgu re produced by 2N + 1 = 21 inﬁnitely narrow

slits. This is the square of the function represented on Figure 11.1.

are linked by

a X





F.T.

−−−→ a

X(aθ),

and hence the (2N + 1) slits are modelized, for instance, wit h the distribution

(x) = a X





·Π



(2N + 1)a



(We took care that the boundaries of the “rectangle” function do not coin-

cide wit h any of the Dirac spikes of the comb, wh ich would have led to an

ambiguity.)

The Fourier transform of a rectangle function with width (2N + 1)a is



(2N + 1)a



F.T.

−−−→ (2N + 1) a

sin



(2N + 1)πaθ



(2N + 1)πaθ

and therefore

(x)

F.T.

−−−→ A

(θ)

with

(θ) =

X(aθ)

∗



(2N + 1) a

sin



(2N + 1)πaθ



(2N + 1)πaθ



= (2N + 1)a



+∞

n=−∞



θ −





∗



sin



(2N + 1)πaθ



(2N + 1)πaθ



that is,

(x)

F.T.

−−−→ A

(θ) = (2N + 1)a

+∞

n=−∞

sin



(2N + 1)π( aθ −n)



(2N + 1)π(aθ −n)

318 Fourier transform of distributions

So the diffraction ﬁgure is given by t he superposition of inﬁnitely many

sine cardinal f unctions centered at k/a with k ranging over Z. But the graph

of the sine cardinal function h as the following shape:

namely, a fairly narrow spike surrounded by small oscillations. One can then

easily imag ine that the whole d iffraction ﬁgure is made of a series of spikes,

spaced at a distance 1/a from each oth er; this is what has b een observed in

Figure 11.1.

Notice that the width of the spikes is proportional to 1/(2N + 1), so the

more slits there are in the diaphragm, the narrower the diffraction bands are. The

number of slits may be read off directly from the ﬁgure, since it corresponds

to the number of local extrema between two main spikes (the latter being

included in the counting). When, as in the example given here, there is an

odd number of slits, the oscillations from neighboring sine cardinals add up;

this implies in part icular that the small diffraction bands between the main

spikes are fairly visible. On the other hand, for an e ven number of slits, the

oscillations compensate for each other; t he secondary bands are then much

less obvious, as can be seen in Figure 11.3, to be compared with Figure 11.1.

Note in passing that we obtained two different formulas for A

, which

are of course equivalent; t his equivalence is, however, dif ﬁcult to prove using

classical a nalytic means.

11.4.d Finitely many slits with ﬁnite width

If we consider now a diaphragm made up of (2N + 1) slits of w idth ℓ (with

ℓ < a so th at the slits are physically separated), its transmittance distribution

can be expressed in the form

(x) =

n=−N



x −na

ℓ







n=−N

δ(x −na)





∗Π



ℓ



that is,

(x) =







·Π



(2N + 1)a



∗Π



ℓ



Application to physical optics 319

-0.5 0.5

Fig. 11.3 — Diffraction ﬁgure of a system with 2N inﬁnitely narrow slits (here 2N =

20). Note that the sec ondary e xtremums are much more attenuated than on

Figure 11.1, where 2N + 1 slits occurred.

(Despite the appearance of the last line, this is a regular distribution.) The

transmittance f

is therefore simply the convolution of the transmittance dis-

tribution f

with a rectangle function with width ℓ. The diffraction ﬁgure

is therefore given by the product of the Fourier transforms of these two dis-

tributions. The Fourier transform of Π(x/ℓ) is a sine cardinal function with

width 1/ℓ. In general, in such systems, th e width of the slits is very small

compared to the spacing, that is, we have ℓ ≪ a. This implies that the width

of this sine cardinal function (1/ℓ) is much larger than the spacing between

the bands. The amplitude of the diffraction ﬁgure

(θ) = A

(θ) ·

sin πℓθ

πℓθ

is shown in Figure 11.4. One sees clearly there how the intensity of the spikes

decreases. Since th e ratio a/ℓ is equal to 4 in this example, the fourth band

from the center is located exa ctly at the ﬁrst minimum of the s ine cardinal,

and h ence vanishes completely.

Remark 11.24 In this last example, three different lengths appear in the problem: the width ℓ

of the slits, the spacing a between slits, and the total length (2N + 1)a of the system. These

three lengths are related by

ℓ ≪ a ≪ (2N + 1)a,

and reappear, in the Fourier world, in the form of the characteristic width 1/ℓ of the disap-

pearance of the bands (the largest characteristic l ength in the diffraction ﬁgure), the distance

1/a between the principal bands of diffraction, and the typical width 1 /(2N + 1)a of the ﬁne

bands (the shortest), with

ℓ

≫

(2N + 1)a

Simply looking at the diffraction ﬁgu re is therefore sufﬁcient in principle to determine

the relative scales of the system of slits in use.

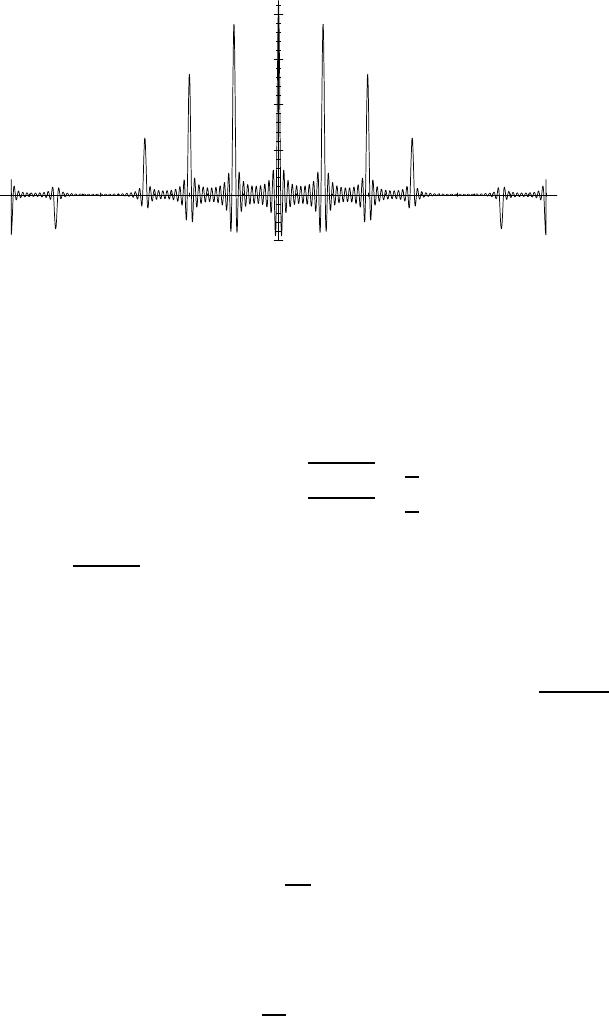
320 Fourier transform of distributions

Fig. 11.4 — Diffraction ﬁgure with 21 slits, with width 4 ti mes smaller than their spacing:

ℓ = a/4.

11.4.e Circular lens

Consider now th e diffraction by a circular lens with diameter D. It is nec-

essary to use here a two-dimensional Fourier transform. The t ransmittance

function of the lens is

f (x, y) =

(

0 if

+ y

1 if

+ y

Since this function is radially symmetric, it is easier to change variables,

putting r

def

+ y

and writ ing f (x, y) = F (r) = H (D/2 −r).

The amplitude A(θ, ψ) of the diffraction ﬁgure is then given by

A(θ, ψ) =

f (x, y) e

−2πi(θx+ψ y)

dx dy,

which is also, substituting (x, y) 7→ (r, ϕ) and deﬁning ρ by ρ =

+ ψ

equal to

A(ρ) = 2π

D/2

r F (r)

−π

−2πiρr cos ϕ

dϕ dr.

DEFINITION 11.25 The Bessel function of order 0 is deﬁned by

∀z ∈ C J

(z)

def

2π

−π

−iz cos ϕ

dϕ

The Bessel function of order 1 is deﬁned by

∀z ∈ C J

(z)

def

iπ

−π

−iz cos ϕ

cos ϕ dϕ

These functions sa tisfy

y J

( y) dy = x J

(x).

Limitations of Fourier analysis and wavelets 321

Fig. 11.5 — The function x 7→ 2 J

(πx)/x. The ﬁrst zero is located at a point x ≈ 1.220,

the second at x ≈ 2.233. The distance between successive zeros decreases.

The amplitude A(ρ) can therefore be expressed as

A(ρ) = 2π

D/2

r J

(2πρr) dr =

2πρ

πDρ

y J

( y) dy =

2ρ

(πDρ)

= S ·



2 J

(πDρ)

πDρ



, with S =

πD

= surface of t he lens.

The graph of the function x 7→ 2 J

(πx)/πx is represented in Figure 11.5.

This function has a smallest positive zero at x ≈ 1.22, which corresponds

to an angle equal to 1.22 λ/D; this is the origin of the numerical factor

in the Rayleigh criterion for the resolution of an optical instrument. The

diffraction ﬁgure has the shape presented in Figure 11.6.

11.5

Limitations of Fourier analysis and wavelets

Fourier analysis can be used to extract from a signal t 7→ f (t) its compos-

ing frequencies. However, it is not suitable for the analysis of a musical or

vocal signal, for instance.

The reason is quite simple. Assume that we are trying to determine the

various frequencies that occur in the performance of a Schubert lied. Then

we have to integrate the sound signal from t = −∞ to t = +∞, which

is already somewhat difﬁ cult (the recording must h ave a beginning and an

ending if we don’t want to spend a fortune in magnetic t ape). If, moreover,

knowing

f we wish to reconstruct f , we must again integrate over ]−∞, +∞[.

Such an integration is usually numerical, and apart from the approximate

knowledge of

f , the integration range must be limited to a ﬁnite interval,

say [−ν

, ν

]. But, even if

f decays rapidly, forgetting the tail of

f may

spectacularly affect the reconstitution of the original signal at th ese instants

when the latter changes very suddenly, which is the case during the “attack”

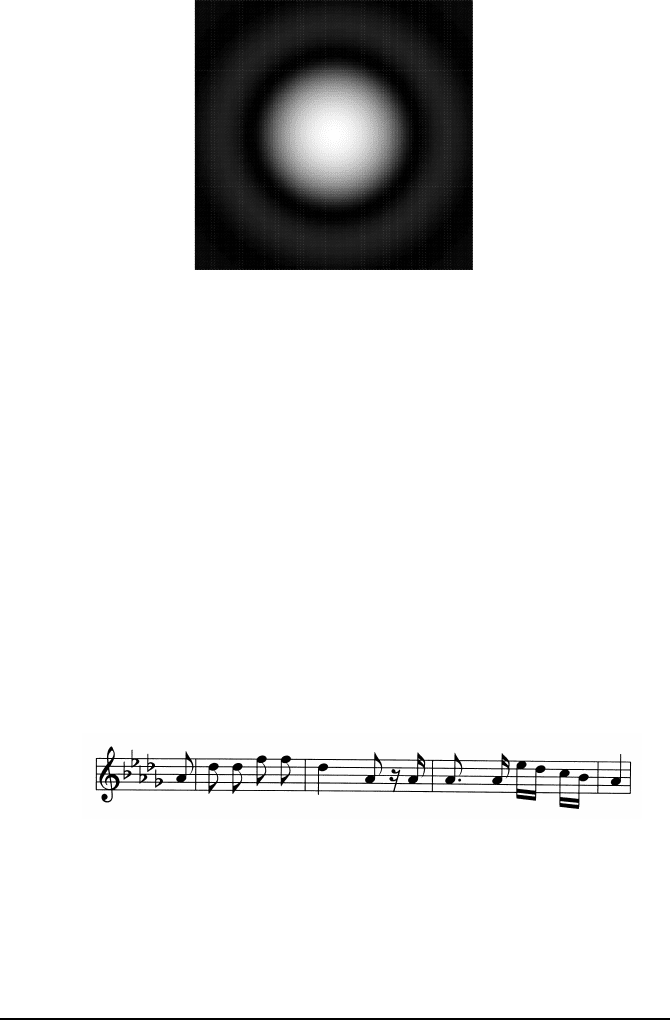
322 Fourier transform of distributions

Fig. 11.6 — The diffraction ﬁgure of a circular lens. Other larger rings appear in practice,

but their intensity is much smaller.

of a note, or when consonants are sung or spoken. Thus, to recreate the attack

of a note (a crucial moment to recognize the timber of an instrument), it is

necessary to compute the function

f (ν) with high precision for large values

of ν, and hence to know precisely th e attack of all the notes in the partition.

When the original signal is recreated, their musical characteristics and th eir

temporal localization may be altered.

This is why some researchers (for instance, the geophysicist Jean Morlet,

Alex Grossman in Marseilles, Yves Meyer at the École Polytechnique, Pierre

Gilles Lemarié-Rieusset in Orsay and then Évry, and many others) have devel-

oped a different a pproach, based on a time-frequency analysis.

We know t hat the modulus of the Fourier spectrum



f (ν)



of a signal

provides excellent information on t he frequency aspects, but little information

on the temporal aspect.

However, to encode a musical signal, the customary

way is to proceed as follows:



−−−−−−−→

On this staff, we can read:

• vertically, the frequency information (the height of the notes);

• horizontally, the timing information (the rhythm, or even indications

concerning attack).

A given signal f (t) and the same translated in time f (t−a) have the same power spectrum,

since only t h e phase changes between the two spectra.

Limitations of Fourier analysis and wavelets 323

The musical signal is therefore encoded in matters of both time and frequency.

Yves Meyer has constructed a wavelet ψ, that is, a function of C

∞

class,

all moments of which are zero, that produces an orthonormal basis (ψ

)

n,p

of L

, wh ere

(t)

def

= 2

n/2

ψ(2

t − p) ∀n, p ∈ Z.

The larger n ∈ Z is, the narrower the wavelet ψ

is; when n → −∞, on

the other hand, the wavelet is extremely “wide.” Moreover, the parameter p

characterizes the average position of the wavelet. The decomposition in the

wavelet basis is given by

f =

+∞

n=−∞

+∞

p=−∞







∀f ∈ L

(R),

in t he sense of convergence in L

. Similarly, a formula analogous to the

Parseval identity holds:

(n,p)∈Z











+∞

−∞



f (t)



dt.

Whereas the “basis” for Fourier expansion was a complex exponential,

which is extremely well localized in terms of frequency

but not localized at

all in time, for wavelets, the time localization is more precise when n is large,

and the f requency localization is wider when n is large. Thus , both time and

frequency information are available. This makes it possible to describe the

attack of a note at time t = t

by concentrating on the wavelet coef ﬁcients

localized around t

; these, even at the highest frequencies, may be computed

without any knowledge of the signal at oth er instants.

Research around wavelets is still developing constantly. The interested

reader is invited to consult the book by Kahane and Lemarié-Rieusset [54]

for a detailed study, or Gasquet [37] for a very clear short introduction, or

Mallat [65] for applications to the analysis of signals. The book by Stein and

Shakarchi [85] should also be of much interest.

A single frequency occurs.

324 Fourier transform of distributions

EXERCISES

 Exercise 11.3 Compute Π(x/a) ∗sin x usi ng the Fourier transform.

 Exercise 11.4 Compute the Fourier transform, in the sense of distributions, of x 7−→ |x|.

 Exercise 11.5 Compute the Fourier transform of H (x) ·x

for any integer n. (One may use

the distributions fp(1/x

), introduced in Exercise 8.6 on page 241.)

 Exercise 11.6 Compute the sum

def

n∈N

+ 4π

−4π

with a, b ∈ R

+∗

The result of Exercise 8.13 on page 243 may be freely used.

 Exercise 11.7 Recall that the Bessel function of order 0 is deﬁned by

(x)

def

2π

−π

−i x cos(θ−α)

dθ for any x ∈ R.

i) Show that this deﬁnition is independent of α. Deduce from this that J

takes real

values.

ii) In the plane R

, let f (x, y) be a radial function or distribution, that is, such that there

exists ϕ : R

→ C (or a distribution with support in R

) with f (x, y) = ϕ(r), where

def

+ y

. Assume moreover that f has a Fourier transform. Show that its Fourier

transform is also radial:

f (u, v) = ψ(ρ) with ρ

def

+ v

Prove the formula gi ving ψ as a function of ϕ, using the Bessel f u nction J

The function ψ is called the Hankel transform of ϕ, denoted ϕ(r)

H. T.

−−→ ψ(ρ).

iii) Show that for continuous functions ϕ and ψ, if ϕ

H. T.

−−→ ψ, the n also ψ

H. T.

−−→ ϕ (i.e.,

the Hankel transform is it s own inverse).

iv) Show that

dϕ

H. T.

−−→ −4π

ψ(ρ).

v) Show that if ϕ

H. T.

−−→ ψ

and ϕ

H. T.

−−→ ψ

, then we have the relation

∞

r ϕ

(r) ϕ

(r) dr =

∞

ρ ψ

(ρ) ψ

(ρ) dρ.

Physical op tics

 Exercise 11.8 Describe the diffraction ﬁgure formed by a system made of inﬁnitely many

regularly spaced slits of ﬁnite width ℓ (the spacing between slits is a).

 Exercise 11.9 Compute, in two dimensions, the diffraction ﬁgure of a diaphragm made of

two circular holes of diameter ℓ, placed at a distance a > 2ℓ.

Exercises 325

PROBLEM

 Problem 5 (Debye electrostatic screen)

• Presentation of the problem

We consider a plasma with multiple components, or in other words, a system of par-

ticles of different types α ∈ I, where I is a ﬁnite set, each type being characterized

by a density ρ

, a mass m

, and a charge e

. (Examples of such systems are an ionic

solution, the stellar matter, the solar wind or solar crown.) I t is assumed that the system

is initially neutral, that is, that

= 0.

The system is considered in nonrelativistic terms, and it i s assumed that the interactions

between particles are restricted to Coulomb interactions. The partic les are also assumed

to be classical (not ruled by quantum mechanics) and point-like . The system may be

described by the following hamiltonian:

H =

i, j

i6= j

i j

with r

i j

def



− r



The indices i and j ranges suc cessively over all p articles in the system.

Now an exterior charge q

, located at r = 0, is added to th e system. We wish to know

the repartition of the other charges where thermodynamic equilibrium is reached.

• Solution of the problem

i) Let ρ

( r ) denote the distribution of density of particles of type α, at equilibrium,

in the presence of q

. Express the distribution q( r ) in terms of the ρ

( r).

ii) Denoting by ϕ( r) the electrostatic potential, write the t wo equations relating

ϕ( r ) and ρ

( r) — the Poisson equation for el ectrostatics and the Boltzmann

equation for thermodynamics.

iii) Linearize the Boltzmann equation and deduce an equation for ϕ( r).

iv) Passing to Fourier transforms, compute the algebraic exp ression of eϕ( k), the

Fourier transform of ϕ( r).

v) Using complex integration and the method of residues, ﬁnd the formula for the

potential ϕ( r), which is called the Debye p otential [2 6].

vi) Show that, at short distances, this potential is indeed of Coulomb type.

vii) Compute the total charge of the system and comment.

326 Fourier transform of distributions

SOLUTIONS

 Solution of exercise 11.2 on page 301 . It must be shown that T (x) = exp(x

) X(x) can-

not act on cert ain functions of the Sc h war tz space. It is easy to check that the gaussian

g : x 7→ exp(−x

) decays rapidly as do all its derivatives, and therefore belongs to S , whe reas

the evaluation of 〈T , g〉 leads to an inﬁnite result.

Strictly speaking, we must exclude also the possibility that there exists another deﬁnition of

〈T , ϕ〉, for ϕ a Schwartz function, which makes it a tempered distribution and coincides with

T (x) ϕ(x) dx for ϕ with bounded support; but t hat is easy by taking a sequence ϕ

of test

functions with compact support that converges in S to g(x). Then on the one hand

〈T , ϕ

〉 → 〈T , g〉

by the assumed conti nuity of T as tempered distribution, and on the other hand

〈T , ϕ

〉 =

T (x) ϕ

(x) dx → +∞,

a contradiction.

 Solution of exercise 11.3. The Fourier transform of the function g iven is

sin πνa

πν





ν −

2π



−



ν +

2π



= 2 sin





ν −

2π



−



ν +

2π



(using the formula f (x) δ(x) = f (0) δ(x)), which, in inverse Fourier transform, gives

2 sin(a/2) sin x.

Of course a direct computation leads to the same result.

 Solution of exercise 11.4. Notice ﬁrst that f : x 7→ |x| is the product of x 7→ x and x 7→

sgn x. The Fourier transform of x 7→ x is, by the differentiation theorem, equal to −iδ

′

/2π.

Moreover, we know that sgn

F.T.

−−−→ pv 1/iπν. Using the convolution theorem yields

x sgn x

F.T.

−−−→

iδ

′

2π

∗

iπ

2π

dν

= −

2π

 Solution of exercise 11.5. The Fourier transforme of the constant function 1 is δ. The

formula F [(−2iπx)

f (x)] = f

(n)

(x) gives

F.T.

−−−→

(n)

(−2iπ)

. and H (x)

F.T.

−−−→

2iπ





The convolution formula then yields

H (x) x

F.T.

−−−→

(n)

2 (−2iπ)

−

(−2iπ)

n+1

dν





Finally, the distribution fp(1/x

n+1

) is linked to the n-th derivative of pv(1/ν) by a multiplicative

constant:

dν





= (−1)

n! f p



n+1



from which we derive

H (x) x

F.T.

−−−→

(n)

2 (−2iπ)

(2iπ)

n+1



n+1

