Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

The Dirac comb 307

11.2

The Dirac comb

11.2.a Deﬁnition and properties

Recall tha t the “Dirac comb” is the distribution d eﬁned by

X(x) =

+∞

n=−∞

δ(x −n).

We can then show —and this is a fundamental result — that

THEOREM 11.21 The Dirac comb is a tempered distribution; hence it has a Fourier

transform in the sense of distributions, which is also equal to the Dirac comb:

X(x)

F.T.

−−−→ X(ν).

This formula can be stated differently; since X is deﬁned as a sum of

Dirac distribiutions, we have

F [X] (ν) = F



+∞

n=−∞



(ν) =

+∞

n=−∞

−2πinν

Renaming “x” th e free variable “ν” (wh ich is perfectly permissible since the

names of the variables are only a matter of choice!) and replacing n by −n , as

we can, we obtain therefore:

+∞

n=−∞

2πinx

+∞

n=−∞

δ(x −n). (11.2)

This formula can be interpreted also as the Four ie r series expansion of XX

XX.

Notice that, in contrast with the case of “usual” periodic functions, th e Fourier

coefﬁcients of this periodic distribution do not converge to 0 (they are all

equal to 1).

Proof of Theorem 11 .21. The theorem is equivalent to the formula (11.2), and we will

prove the latter.

Let f (t) =



Π(t)



∗X(t). This is indeed a functio n, and its graph is

f (t) =

−1 −

308 Fourier transform of distributions

As a periodic function, f can be expanded in Fourier series. Since f is even, only the

cosine coefﬁcients a

occur in this expansion, and after integrating by parts twi ce, we

get

= 4

1/2

cos(2πnx) dx

= −4

1/2

πn

sin(2πnx) dx +



sin(2πnx)

2πn



1/2

(the boundary terms vanish)

= −

πn

1/2

cos(2πnx)

2πn

dx +



(2πn)

cos(2πnx)



1/2

, (and t he integral also)

that is,

(−1)

Moreover, differentiating twice the function f , in the sense of distributions, we obtain

ﬁrst

′

(t) =

−1 −

−1

and then

′′

(t) = 2 −2

+∞

n=−∞



x −n −



= 2 −2 X



x −



Hence, differentiating twice the series f (t) =

∞

n=0

cos(2πnt) yields

2 −2X(x −

) = −4

+∞

n=1

(−1)

2πinx

X(x −

) = 1 + 2

+∞

n=1

(−1)

2πinx

and therefore

X(x) = 1 + 2

+∞

n=1

(−1)

2πinx

iπn

= 1 + 2

+∞

n=1

2πinx

+∞

n=−∞

2πinx

(since X is even), which was to be proved.

11.2.b Fourier transform of a periodic function

The case of a periodic function seems at ﬁrst sight to require some care, since

a 2π-periodic function f (for instance), only belongs to L

(R) or L

(R) if is

almost everywhere zero. However, any f unction in L

[0, a] deﬁnes a tempered

distribution, and therefore has a Fourier transform.

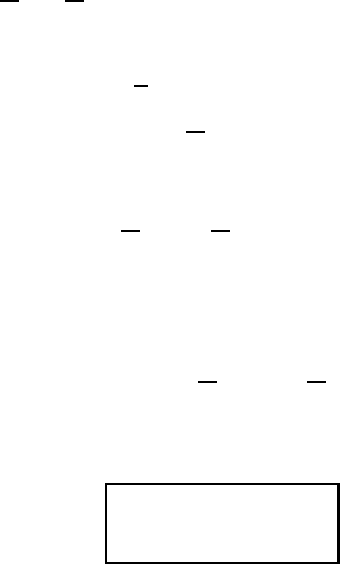
The Dirac comb 309

So take f ∈ L

[0, 1], which can be expanded in a Fourier s eries

f (x) =

+∞

n=−∞

2πinx

which converges to f in quadratic mean. By linearity, we easily compute the

Fourier transform of such a series,

f (ν) =

+∞

n=−∞

δ(ν −n). (11.3)

Hence the Fourier coefﬁcients of a function in L

[0, 1] occur as the

“weights” of the Dirac distr ibutions which appear in its Fourier transform.

This is what is observed when a periodic signal (for instance, a note which is

held on a musical instrument) is observed on a modern oscilloscope which

computes (via a fast Fourier transform) the spectrum of the signal.

11.2.c Poisson summation formula

Let f be a continuous function and T an arbitrary nonzero real number.

Assume that the following convolution exists:

f (x) ∗





= f (x) ∗

+∞

n=−∞

δ(x −nT ) =

+∞

n=−∞

f (x −nT )

(it sufﬁces, for instance, that f decays faster than 1/|x| at inﬁnity). The

Fourier transform of f (x) ∗

X (x/T ) is

f (ν) ·

X(T ν), or equivalently

n∈Z





δ(T ν −n),

the inverse Fourier transform of which is equal to

n∈Z





2iπnx/T

THEOREM 11.22 (Poisson summation for mula) L et f be a continuous function

which has a Fourier transform. Wh en the series make sense, we have

+∞

n=−∞

f (x −nT ) =

+∞

n=−∞





2iπnx/T

In the special case x = 0 and T = 1, the Poisson summation formula is

simply:

+∞

n=−∞

f (n) =

+∞

n=−∞

f (n).

310 Fourier transform of distributions

11.2.d Application to the computation of series

Take, for inst ance, the problem of computing the sum of the series

def

∞

n=−∞

+ 4π

with a, b ∈ R

∗+

and a 6= b. First, note that if we deﬁne

S(τ)

def

∞

n=−∞

+ 4π

2πinτ

for all τ ∈ R,

then we have S = S (0) and we can write

S(τ) =

∞

n=−∞

f (n) e

2πinτ

with

f (ν) =

4π

+ a

4π

+ b

= eg(ν) ·

h(ν).

To exploit the Poisson summation formula, it is necessary to compute the inverse Fourier

transform of f and hence those of g and h. We know th at

−a|x|

F.T.

−−−→

+ 4π

and therefore we deduce th at

g(x) =

−a|x|

and h(x) =

−b|x|

2 b

From this we can compute f : indeed, from

f = eg ·

h it follows that f = g ∗h; this convolution

product is only an elementary (tedious) computation (see Exercise 7.5 on p age 211) and yields

f (x) =

4ab

−a|x|

∗e

−b|x|

−a



−a|x|

−

−b|x|



Hence we have

S = S(0) =

+∞

n=−∞

f (n) =

∞

n=−∞

f (n)

−a

∞

n=−∞

−a|n|

−

−a

2 b

∞

n=−∞

−b|n|

Each series is the sum of two geometric series (one for positive n and one for negative n), and

we derive after some more work that

∞

n=−∞

−a|n|

1 + e

−a

1 −e

−a

and

∞

n=−∞

−b|n|

1 + e

−b

1 −e

−b

Hence, after rearranging the terms somewhat , we get

S =

−a



1 −e

−a

−

1 −e

−b



−

2ab

b + a

2(b

−a

)



coth a

−

coth b



I did not make it up for the mere pleasure of computing a series; it appeared during a

calculation in a ﬁnite-temperature quantum ﬁeld theory problem.

The Gibbs phenomenon 311

Josiah Willard Gibbs (1 839—1903), American physicist, was pro-

fessor of mathematical physic s at Yale University. Gibbs revo-

lutionized the study of thermodynamics in 1873 by a geometric

approach and then, in 1876, by an article concerning the equilib-

rium properties of mixtures. He had the idea of using diagrams

with temperature–entropy coordinates, where the work duri ng a

cyclic transformation is given by the area of the cycle. It took

a long t ime for chemists to understand the true breadth of this

paper of 1876, which was written in a mathematical spirit. G ibbs

also worked in pure mathematics, in particular i n vector analy-

sis. Finally, his works in statistical mechanics helped provide its

mathematical basis.

11.3

The Gibbs phenomenon

Although the Gibb s phenomenon may be explained purely with the tools

of Fourier series,

it is easier to take advantage of t he Fourier transform of

distributions to clar ify things.

Let f be a function, with Fourier transform

f (ν) and denote

(x) =

−ξ

f (ν) e

2πiν x

dν

for any ξ > 0. To obtain f

, the process is therefore:

• decompose f in its spectral components

f (ν);

• remove the higher frequencies (those with |ν| > ξ );

• reconstruct a function by summing the low-frequencies part of the spec-

trum, “forgetting” about the higher frequencies (which characterize the

ﬁner details of the f unction).

So we see that the function f

is a “fuzzy” version of the original func-

tion f . It can be expressed as a convolution, since

= F

−1



Π(ν/2ξ ) ·

f (ν)



= f (x) ∗

sin 2πξ x

πx

Now recall tha t, in the sense of distributions, we have

lim

ξ→+∞

sin 2πξ x

πx

= δ(x),

Using, for instance, the Dirichlet kernel, as in [8].

312 Fourier transform of distributions

in accordance with the result stated on page 233, which proves that, by for-

getting frequencies at a higher and higher level, we will ﬁnally recover the

original signal:

lim

ξ→+∞

= f (in the sense of distributions).

In the case where f has a discontinuity at 0, we can simply write f =

g +αH , where α is the “jump” at the discontinuity and g is now a continuous

functions. Now let us concentrate on what happens to H when put through

the ﬁltering process d escribed above. We compute

(x) = H (x) ∗

sin 2πξ x

πx

−∞

sin 2πξ y

π y

dy =

Si(2πξ x), (11.4)

where Si is the sine integral, deﬁned (see [2, 42]) by the formula

Si(x)

def

sin t

dt.

If we plot the graph of H

(x) =

Si(2πx), we can see oscillations, with

amplitude around 8% of the unit height, on each side of the discontinuity.

0,2

0,4

0,6

0,8

−2

−1 1

2 3

When the cutoff frequency is increased, formula (11.4) shows that t he size

of the oscillations remains constant, but that they are concentrated in the

neighborhood of the point of discontinuity (here, we have ξ = 2, 3, 4, 5 and

the graph has been enlarged in t he horizontal direction to make it more

readable):

Notice in passing that a low-pass ﬁlter in frequencies is not physically po ssible, since it is

not causal.

The Gibbs phenomenon 313

0,5

1 2 3

What happens now if we consider a function f which is 1-periodic, piece-

wise continuous, and piecewise of C

class? Then f has a Fourier series

expansion

f (x) =

n∈Z

2πinx

which corresponds to a Fourier transform

f (ν) =

n∈Z

δ(ν −n).

Then the function f

, obta ined by removing from t he spectrum the frequen-

cies |ν| ¶ ξ , is none other t han

(x) =

|n|¶ξ

2πinx

that is, the partial sum the Fourier series of f of order E[ξ ] (integ ral part

of ξ ).

Hence the sequence of partial sums of the Fourier series will exhibit the

same aspect of oscillations with constant amplitude, concentrated closer and

closer to the discontinuities.

It should be noted that this phenomenon renders Fourier series rather

unreliable in numerical computations, but that it can be avoided by using,

instead of the partial s ums of the Fourier series, the Cesàro means of those

series, wh ich are called Fejér sums (see Exercise 9.4 on page 270).

In the preceding example wi th the Heaviside function, the oscillations get narrower in

a continuous manner. Here, since the fu nct ion, being 1-periodic, has really inﬁnitely many

discontinuities, there ap pears a superposition of oscillating ﬁgures which has th e p roperty,

rather unintuitive, of remaining “ﬁxed” on the intervals ξ ∈ [n, n + 1[ and of changing

rapidly when going through the points ξ = n.

314 Fourier transform of distributions

11.4

Application to physical optics

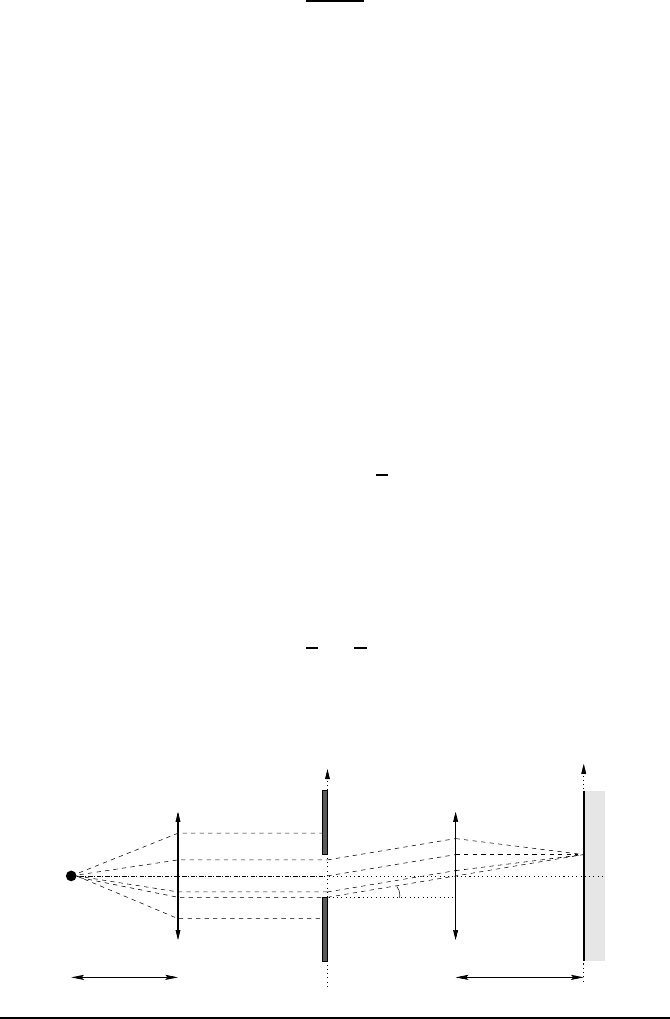
11.4.a Link betw een diaphragm and diffraction ﬁgure

We are going to investigate the phenomenon of light diffraction through a

diaphragm. For th is purpose, consider an experiment that gives the possibility

of observing t he diffraction at inﬁnity (i.e., the diffration corresponding to

the Fraunhofer approximation; see [14] for a detailed study), with a ligh t

source S considered as being purely monochromatic.

To simplify matters, we consider a system which is invariant under trans-

lation along t he O y axis. The diaphragm, placed at th e focal point of a lens

(with focal length F on th e ﬁgure), is characterized by a transmittance f unc-

tion f (x) which expresses the ratio between the light amplitude just in front

and b ehind the diaphragm. Typically, this transmitt ance function is a charac-

teristic function. For instance, a slit of length ℓ (inﬁnitely long) is modeled

by a transmittance function equal to

slit

(x) = Π



ℓ



However, it may ha ppen that one wishes to model an inﬁnitely narrow slit. In

order to still be able to observe a ﬁgure, it is required to increase the intensity of

the light arr iv ing in inverse proportion to t he width of the slit. This intensity

coefﬁcient is incorporated to the the transmittance, which gives

slit

= lim

ℓ→0

ℓ



ℓ



= δ(x).

With this convention, t he “transmittance function” thus becomes a “transmit-

tance distribut ion.”

Nonmonochromatic effects will the studied in Section 13.7 on page 371

Application to physical optics 315

The amplitude which is observed in the direction α is, wit h the Fraunhofer

approximation and linearizing sin α ≈ α, equal to

f (x) e

−2πiαx/λ

dx,

up to a multiplicative constant. On a screen at the focal point of a lens with

focal length R, the amplitude is therefore equal to

A( y) = C

f (x) e

−2πi yx/Rλ

dx.

Changing the scale for the screen and putting θ = y/Rλ, wh ich has the

dimension of the inverse of length, we obtain therefore

A(θ) = C

f (x) e

−2πiθx

dx =

f (θ).

Hence, up to a multiplicative consta nt (which we will ignore in our computa-

tions from now on), the amplitude of the diffraction ﬁgure at inﬁnity of a diaphragm

is given by the Fourier transform of its transmittance distribution.

Remark 11.23 From the mathematical point of view, interference and dif fraction phenomena

are strictly equivalent.

11.4.b D iaphragm made of inﬁnitely many

inﬁnitely narrow slits

Consider a diaphragm made of inﬁnitely many slits, placed at a ﬁxed dis-

tance a from ea ch other, with coordinates equal to na wit h n ranging over all

integers in Z. The diaphragm is modeled by a “Dirac comb” distribution

(x) =

n∈Z

δ(x −na) =

n∈Z

a δ



−n



= a X





The diffraction ﬁgure produced by the diffraction a pparatus thus described is

then (in terms of amplitude) given by the Fourier transform of

(x) = a X





F.T.

−−−→ A

(θ) = a

X(aθ).

In other words, inﬁnitely many inﬁnitely narrow slits produce a diffraction

ﬁgure consisting of inﬁnitely many inﬁnitely narrow bands. T he step between

bands is 1/a.

Thus, using the properties of the Fourier transform, we notice that the larger

the spacing between the slits, the smaller the spacing between the steps of the diffraction

ﬁgure.

Of course, the situation described here is never seen in practice, as there

can only be ﬁnitely many slit s, and they are never inﬁnitely narrow.

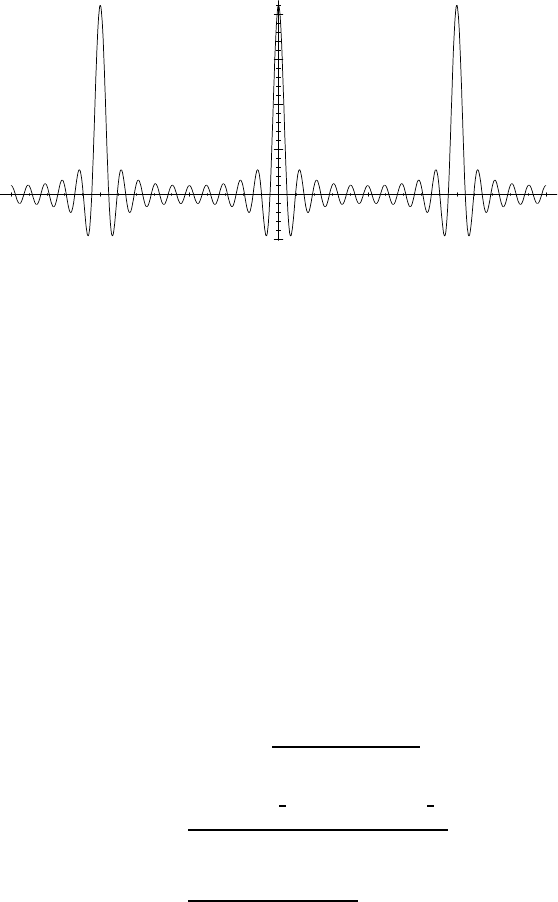
316 Fourier transform of distri butions

-1

-0,5 0,5

1 1,5

Fig. 11.1 — Amplitude of the diffraction ﬁgure given by 2N + 1 = 21 inﬁnitely narrow slits.

11.4.c Finite number of inﬁnitely narrow slits

Consider now a diaphragm made of 2N + 1 slits, separated by a ﬁxed dis-

tance a. The coordinates of the slits are then −Na, . . ., −a, 0, a, . . ., Na.

The transmittance of the diaphragm is then modeled by

(x) =

n=−N

δ(x −na).

The dif fraction ﬁgure is the Fourier transform of f

, which may be com-

puted by summing directly the Fourier transforms of each Dirac component:

(θ) =

n=−N

−2πinaθ

or, s umming the partial geometric series,

(θ) = e

2πiaθN



1 −e

−2πiaθ(N +1)

1 −e

2πiaθ



2πiaθ



N+



−e

−2πiaθ



N+



iπaθ

−e

−iπaθ

sin



(2N + 1)πaθ



sin πaθ

. (11.5)

This function can be checked to be continuous (by extending by continuity).

It is represented in Figure 11.1; the corresponding intensity is represented in

Figure 11.2. The shape of this curve is, however, not easy to “see” obviously

by just looking at formula (1 1.5).

The amplitude A

may als o be ob tained using the convolution formulas.

Indeed, the transmitt ance and the diffraction ﬁgure for inﬁnitely many slit s