Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Solutions of exercises 247

−3 −2

−1 1

2 3

Fig. 8.6 — The sequence of functions f

: x 7−→



sin πnx/2

sin πx/2



, for n = 2, . . . ,7. The

limit in t he sense of distributions of this se quence is X.

 Solution of exercise 8 .10. We have δ

= δ(r − R). On t h e other hand,

δ(r

− R

) =

2 R

δ(r −R) =

2 R

 Solution of exercise 8 .11. By writing the difference of two consecutive terms and integrat-

ing by parts, it follows that

−1

(t) dt is independent of n. Hence (see the graph in Figure 8.6)

−1

(t) dt = 1 ∀n ∈ N.

Moreover, f

takes only positive values and converges u niformly to 0 on any interval of th e type

]+ǫ, 1], with ǫ > 0, which shows th at





(x) −−→

n→∞

δ,

and since f

(x) =

+∞

k=−∞



x−k



(x) and each term tends to δ

, it follows that f

−−→

n→∞

Of course, it is possible to ﬁnd simpler sequences of functions that converge weakly to X

in D

′

, for instance, the sequence of functions

(x) = n Π



x − E(x)



 Solution of exercise 8 .13. Expand the sine as sum of two complex exponentials, rearrange

the terms, and compute the sums of geometric series. The convergence must be justiﬁed.

 Solution of exercise 8 .15. We have E(x, t) = H (x) H (t) and therefore

∂ E

∂ x

(x, t) = δ(x) H (t),

248 Distributions II

whence

∂

∂ x∂ t

(x, t) = δ(x) δ(t).

As for the laplacian, it is equal to △E = δ

′

(x) H (t) + H (x) δ

′

(t).

 Solution of exercise 8 .16.

i) The force exerted on the truck by the spring is k ·



E(vt) −R(t)



, so by Newton’s law

we can write

(t) + k ·



R(t) − E(vt)



= 0,

hence the required formula.

ii) The previous equation can also be written



′′

+ ω



∗ R = ω

E(vt),

and remains valid if E is a distribution. The choice of D

′

is justiﬁed by the desire to

study a causal system. More precisely, if the excitati on (the road) starts at a ﬁnite time in

the past, we want the response to be identically zero before that time. The convolution

inverse of



′′

+ ω



in D

′

has this property.

iii) In D

′

, the solutions are given by R(t) = E(t) ∗ωH (t) sin ωt.

• In the case of a narrow bump, we have E(t) = δ(vt) = δ(t)/v and R(t) =

(ω/v)H (t) sinωt.

• For a ﬂat road, we ﬁnd R(t) = ℓH (t)[1 −cos ωt].

• For a wavy road, denoting ω

′

= v/λ we obtain

R(t) = ω

sin(ωs) sin



′

(t − s)



ds = ωℓH (t)

ω sin(ω

′

t) −ω

′

sin(ωt)

−ω

′2

iv) The nitroglycerin will explode if the amplitudes of the vibrations of the truck are too

important. The previ ou s formula indicates a resonance at the speed v = λω. A very

slow or very fast speed will avoid this resonance.

 Solution of problem 3. Using Theorem 7.51 on page 206, the formula asked in Ques-

tion 2 follows. To show that (△+ k

) G = δ, use the property

△(1/r) = −4π δ

and the formula for differentiating a product: it follows that

Φ( r) =



( r) +



dϕ



, δ

( r)



∗

(−1)

4π

ikr

and then that

Φ( r) =



( x) +



dϕ



( x),

(−1)

4π

ikkr −xk

kr − xk



Chapter

Hilbert spaces,

Fourier series

9.1

Insufﬁciency of vector spaces

To indicate how vector spaces and the usual notion of basis (which is called

an algebraic basis) are insufﬁcient, here is a little problem: let E = R

, the

space of sequences of real numbers. Clearly E is an inﬁnite-dimensional vector

space. So, the general theory of linear algebra teaches that

THEOREM 9.1 Any vector sp ace has at least one algebraic basis.

The question is then

Can you describe a basis of E?

(Before turning t he page, you should try your skill!)

Though the theorem that states this does not give a way of constructing such a basis. Even

worse, the proof uses the axiom of choice — or rather an equivalent version, cal led Zorn’s le mma

LEMME (Zorn) Let Z be a non-empty ordered set in which any totally ordered subset admits an upper

bound in Z. Then Z contains at least one maximal element.

An elegant statement certainly, but w h ich, for a physici st, looks obviously ﬁshy: not much

that is constructive will come of it!

250 Hi lbert spaces; Fourier series

Let’s try. One may think that the family

(1, 0, 0, 0, . . . ), (0, 1, 0, 0, . . .), (0, 0, 1, 0, . . .), . . .

(9.1)

of elements of E is a basis. But this is an illusory hope, remembering that a

basis is a free and generating family:

DEFINITION 9.2 (Algebraic basis) L et I be an arbitrary index set (ﬁnite,

countable, or uncountable). The s ub-vector space generated by a family

)

i∈I

of vectors in a vector space E, denoted Vect



; i ∈ I



, is the set of

( ﬁnite, by deﬁnition) linear combinations of t hese vectors:

Vect



; i ∈ I



def

x =

i∈I

′

; I

′

⊂ I ﬁnite and a

∈ K

If Vect{x

; i ∈ I} = E, the family (x

)

i∈I

is called a generating family, and

the family (x

)

i∈I

is free if t he only (ﬁnite) linear combination which is equal

to z ero is the one where every coefﬁcient is zero.

The family (x

)

i∈I

is an algebraic basis if it is both free and generating.

This means that any element of E must be expressible as a ﬁnite linear

combination of the basis vectors. But it is clear that (1, 1, 1, . . . , 1, . . .), which

is an element of E, is not a ﬁnite linear combination of the family (9.1).

Finite sums, schminite sums! We just need to suppress this condition of

ﬁniteness and permit inﬁnite sums. But what this means needs to be clariﬁed.

More precisely, we must give a meaning to t he convergence of a sum

∞

i=0

where the α

are scalars and the e

are vectors.

To speak of convergence, the simplest solution is to consider the setting

of normed vector spaces. Indeed, on th e space E of real sequences, there is a

natural norm associated to the scalar product

〈u, v〉 =

∞

k=0

, namely, kuk

∞

k=0

However, this will not do, since the norm of the vector (1, 1, 1, . . ., 1, . . . )

is inﬁnite. Without additional assumptions, speaking of norms brings other

difﬁculties, and we are back at the beginning. Well, then, one may wish

to keep the ﬁniteness requirement for the sums, but to restrict the vector

space under consideration by looking only at the space E

made of sequences

with bounded support (i.e., sequences where all but ﬁnitely many elements

are zero). This time, the family (9.1) is indeed a n a lgebraic basis of E

, but

Pre-Hilbert spaces 251

another unpleasant phenomenon arises. Consider the sequence

(1)

= (1, 0, 0, 0, 0, . . . ), x

(2)



, 0, 0, 0, . . .



(3)



, 0, 0, . . .



, x

(4)



, 0, . . .



(n)



, . . . ,

n−1

, 0, . . .



, . . .

of elements of E

If we put

x =





k∈N

∗



, . . . ,

n−1

, . . .



it seems “obvious” that the sequence (x

(n)

)

converges to x, since



(n)

− x



∞

k=n

3 ·4

n−1

Unfor tunately, the element x does not belong to E

(it does not have bounded

support). One says that E

is not complete.

So we can see that t he difﬁculties pile up when we try to extend the notion

of basis to an inﬁnite family of vectors. To stay in a “well-behaved” setting, we

are led, following Hilbert and Schmidt, to introduce the notion of a Hilbert

space. Before doing this, we will review the general techniques linked to the

scalar product a nd to projection onto subspaces of ﬁnite dimension.

9.2

Pre-Hilbert spaces

DEFINITION 9.3 Let E be a real or complex vector space. A complex scalar

product or a hermitian (scalar) product on E is any application (form)

(x, y) 7→ (x|y) such that

(a) (x|y) = ( y|x) for all x, y ∈ E;

(b)





α y + y

′



= α (x|y) +





′



for any α ∈ C, and x, y, y

′

∈ E;

(d) (x|x) = 0 if and only if x = 0.

If E is equipped with a hermitian product, it is called a pre-Hilbert space.

252 Hilbert spaces; Fourier series

Property (b) expresses the linearity with respect to the second variab le.

The scalar product is thus semilinear (or antilinear) with respect to the ﬁrst,

which means that

∀α, β ∈ C, ∀x, x

′

, y, ∈ E



αx + βx

′





= α (x|y) + β



′





The hermitian product is also called deﬁnite (property d) and positive (prop-

erty c).

DEFINITION 9.4 (Norm) L et E be a pre-Hilbert space. The norm (or hermi-

tian norm) of an element x ∈ E is deﬁned using the scalar product by

kxk

def

(x|x).

(Theorem 9.6 on the facing page shows that this is indeed a norm.)

The hermitian product has the following essential property:

THEOREM 9.5 (Cauchy-Schwarz

inequality) Let E be a p re-Hilbert space. Let

x, y ∈ E be two vectors. Then we have



(x|y)



¶ kxk·kyk,

with equality if and only if x and y are colinear.

Proof. Put θ

def

(

)

(assuming that (x|y) 6= 0, which is not a restriction since

otherwise the inequality is immediate). Then we h ave θθ = 1 and, for any real number

λ, the inequalities

0 ¶ (θx + λ y|θx + λ y) = θθ (x|x) + θλ (x|y) + λθ ( y|x) + λ

( y|y)

= λ

( y|y) + 2λ |(x|y)|+ (x|x) .

If kyk

6= 0 (otherwise the result is also proved), this last quantity is a polynomial

of degree 2 in λ, positive or zero for any value of λ ∈ R; this is only possible if the

discriminant is negative, namely, if

4 |(x|y)|

−4 ( y|y) (x|x) ¶ 0,

or equivalently if |(x|y)| ¶

(x|x)

( y|y), which is the required inequality. Moreover,

there is equality if and only if the polynomial has a double root; in that case, taking

λ to be equal to thi s root, we obtain



θx + λ y



= 0, which shows that the vectors x

and y are linearly dependent.

Another importance inequality, called the Minkowski inequality, shows that

the map x 7→

(x|x) is indeed a norm (in the sense deﬁned in Appendix A):

One should not confuse Hermann Schwarz (1843—1921) and Laurent Schwartz (1915—

2002). For biographical indications, see, respectively, pages 161 and 222.

Pre-Hilbert spaces 253

THEOREM 9.6 (Minkowski inequality) Let E be a pre-Hilbert space. Then we

have

∀x, y ∈ E kx + yk ¶ kxk+ kyk,

with equality if and only if x a nd y are linearly dependent, and their proportionality

coefﬁcient is positive or zero.

Proof. Use the Cauchy-Schwarz inequality in the expansion of kx + yk

Moreover, we have the following equality:

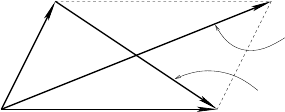
THEOREM 9.7 (Parallelogram identity) If E is a pre-Hilbert space, then for any

x, y ∈ E we have

kx + yk

+ kx − yk

= 2 kxk

+ 2 kyk

This is called the the parallelogram identity (or law) because of the following

analogy with the euclidean norm in the plane: the sum of the squares of the

lengths of the diagonals of a parallelogram is equal to the sum of the squares

of the lengths of th e four sid es.

x − y

x + y

DEFINITION 9.8 (Orthogonality) Let E be a pre-Hilbert s pace.

i) Two vectors x and y in E are orthogonal if (x|y) = 0. This is denoted

x ⊥ y.

ii) Two subsets A and B are orthogonal if , for any a ∈ A and any b ∈ B,

we have a ⊥ b. This is denoted A ⊥ B.

iii) If A is an arbitrary subset of E, the orthogonal of A, denoted A

⊥

, is

the vector space of elements in E which are orthogonal to all elements

of A:

⊥



x ∈ E ; ∀y ∈ A, x ⊥ y



DEFINITION 9.9 (Orthonormal system) Let E be a pre-Hilbert space and let

)

i∈I

be an arbitrary family of vectors of E indexed by a set I that may or

not be countable. The family (e

)

i∈I

• an orthogonal system if (e



) = 0 as soon as i 6= j;

• an orthonormal system if (e



) = δ

i j

for all i, j.

254 Hilbert spaces; Fourier series

9.2.a The ﬁnite-dimensional case

We assume in this section that E is a pre-Hilbert s pace of ﬁnite dimension

(which is also called a hermitian space in the complex case and a euclidean

space in the real case).

Now let (e

, . . . , e

) be a given orthonormal basis of E

. If x is any vector

in E, it can be decomposed according to t his basis : x =

. Computing

the scalar product of x with one of the ba sis vectors e

, we obtain, using t he

linearity on the rig ht of the scalar product

|x) =





i=1



i=1

) =

i=1

i,k

= x

Hence, the coordinates of a vector in an ort honormal basis are simply given

by the scalar products of this vector with ea ch basis vector.

Similarly, if x and y are vectors, their scalar product is

(x|y) =



i=1



j=1



i, j=1



)

|{z}

i, j

i=1

THEOREM 9.10 (Computations in orthonormal basis) Let (e

, . . . , e

) be an or-

thonormal basis of E. T hen, for any x, y ∈ E, we have

x =

i=1

|x) e

, i.e., x

= (e

|x) ,

(x|y) =

i=1

(x|e

) (e

|y) , kxk

i=1

9.2.b Projection on a ﬁnite -dimensional subspace

In any pre-Hilbert space, the techniques of the previous section provide a

means to project an arbitrary vector on a subspace V of ﬁnite d imension p.

For this, let (e

, . . . , e

) be an orthonormal basis of V . D eﬁne then

def

i=1

|x) e

Then x

is an element of V . Moreover, (x − x

) = 0 for k = 1, . . ., p,

hence x − x

is orthogonal to V . Finally, for a ny y ∈ V , since y − x

in V , hence orthogonal to x − x

, we can apply Pythagoras’ theorem and get

kx − yk

= kx − x

+ ky − x

¾ kx − x

To show that such a basis exists is easy: just take an arbitrary basis, then apply the Gram-

Schmidt alg orithm to make it orth o normal.

Pre-Hilbert spaces 255

The dista nce from x to V , which is deﬁned by d(x; V ) = inf

y∈V

kx − yk, is

therefore attained at a unique point, which is none other than x

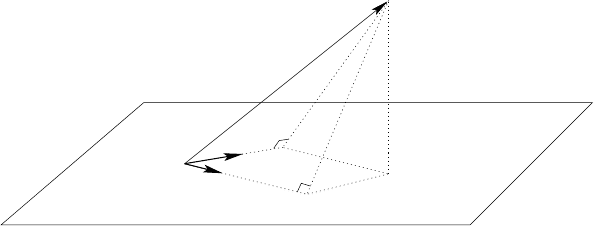
THEOREM 9.11 (Orthogonal projection theorem) Let E be a pre-Hilbert sp ace

of arbitrary dimension. Let V be a subspace of E of ﬁnite dimension. For x ∈ E,

there exists a unique element x

in V such that x − x

⊥ V , which is given by the

orthogonal projection of x on V , deﬁned by

def

i=1

|x) e

for any orthonormal basis (e

, . . . , e

) of V .

Moreover, x

is the unique vector in V such that d(x; V ) = kx − x



x) e



x) e

THEOREM 9.12 (Orthogonal c omplement) Let V be a ﬁnite-dimensional sub-

space of E.

i) V

⊥

is a complementary subspace of V , called the orthogonal complement

of V :

E = V ⊕ V

⊥

ii) The orthogonal of V

⊥

is V : V = (V

⊥

)

⊥

Proof

i) It is immediate that V ∩ V

⊥

= {0}. Moreover, any vector x is decomposed in

the form x = x

+ (x − x

), where the ﬁrst vector is an element of V and the

second an element of V

⊥

, whic h shows that E = V ⊕ V

⊥

ii) The inclusion V ⊂ (V

⊥

)

⊥

is clear.

Let now x ∈ V

⊥⊥

. Using the known decomposition E = V ⊕ V

⊥

, we can

write x = y + z with y ∈ V and z ∈ V

⊥

.Then z is orthogonal to any vector

of V ; in particular, ( y|z) = 0, that is (x − z|z) = 0. But x is orthogonal to V

⊥

so (x|z). Thus (z|z) = 0: it follows that z = 0, so x = y and hence x ∈ V as

desired.

256 Hilbert spaces; Fourier series

Remark 9.13 If V is a subspace of inﬁnite dimension, the previous result may be false. For

instance, consider t he pre-Hilbert space E of continuous functions on [0, 1], with the natural

scalar product ( f |g) =

f g, and the subspace V of functions f such that f (0) = 0. If

g is a function in V

⊥

, then it is orthogonal to x 7→ x g(x) (which belongs to V ); therefore



g(x)



dx = 0 and g = 0. Therefore V

⊥

= {0}, although {0} is not a complementary

subspace of V .

9.2.c Be ssel inequality

Let E be a pre-Hilbert space. Consider a countable orthonormal family of E.

For a vector x ∈ E, we denote

def

n=0

|x) e

for any p ∈ N,

the or thogonal projection of x on the ﬁnite-dimensional subspace V

Vect{e

, . . . , e

}. Since x − x

⊥ Vect{e

, . . . , e

}, Pythagoras’ theorem implies

that

kxk



x − x



, and hence



n=0



(x|e

)



¶ kxk

Since this inequality holds for all p ∈ N, we deduce:

THEOREM 9.14 (Bessel inequality) Let E be a pre-Hilbert spa ce. Let (e

)

n∈N

a countable orthonormal system and let x ∈ E. Then the series



|x)



converges

and we have

∞

n=0



|x)



¶ kxk

9.3

Hilbert spaces

Recall that a normed vector space E is complete if any Cauchy sequence

in E is convergent in E.

Complete spaces are important in mathematics, because the notion of

convergence is much more nat ural in such a space. These are therefore the

spaces that a physicist “requires” intuitively.

Since the formalization of quantum mechanics by János (John) von Neumann (1903—1967)

in 1932, many physics courses start with the following axiom: The space of states of a quantum

system is a Hilbert space.