Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Fourier series expansion 267

[0, a] , it is perfectly possible to deﬁne the coefﬁcient

def

f (t) e

−2πint/a

dt,

since a function is Lebesgue-integrable if and only if its modulus is integrable.

Hence:

PROPOSITION 9.43 For any function f ∈ L

[0, a] , the Fourier coefﬁcients of f

are deﬁned.

It is then possible to construct the sequence ( f

)

n∈N

of partia l Fourier

sums of f . What is it possible to say about this sequence? Since we have left

the setting of Hilbert spaces, the general results such as Theorem 9.21 can not

be applied. We will subdivide this problem into several questions.

9.4.d Pointwise convergence of the Fourier series

☞ First question: is it true that the coefﬁcients c

tend to 0?

This is not a mathematician’s gratuitous question, but rather a crucial

point for the practical use of Fourier series: in an approximate computation,

it is importa nt to be able to truncate the series and compute only with ﬁnitely

many terms. A necessary (but not sufﬁcient) condition is therefore that c

→ 0

as [n → ±∞].

The (posit ive) answer is given by the celebrated Riemann-Lebesg ue lemma

(a more general version of which will be given in the next chapter, see Theo-

rem 10.12):

THEOREM 9.44 (Riemann-Lebesgue lemma) Let f ∈ L

[0, a] be an integrable

function. Then we have

f (t) e

2πint/a

dt −−−−→

n→±∞

Proof. The proof is in two steps.

• Consider ﬁrst th e case where f is of C

class; a simple integration by parts implies

the result as follows:

f (t) e

2πint/a

dt =

2πn

′

(t) e

2πint/a

dt +

2πn



f (a) − f (0)



which, since f and f

′

are both bounded by assumptions, tends to 0 as n tends to

inﬁnity (the integral i s bounded).

• Then this is extended to all integrable functions by showing that the space of

functions of C

class is dense in L

[0, a], for instance, by applying the theorem of

regularization by convolution (t ake convolutions o f f ∈ L

[0, a] by a gaussian with

variance 1/p and norm 1, whe re p is sufﬁciently large so that



f − f ∗ g



¶ ǫ).

This is technically delicate, but without conceptual difﬁculty.

268 Hilbert spaces; Fourier series

Joseph Fourier (1768—1830) studied at the Royal Military School

of Auxerre and, from the age of thirteen, showed an evident inter-

est for mathematics, although he was tempted to become a priest

(he entered a se minary at Saint-Benoît-sur-Loire, which he left in

1789). In 1793, he joined a revolutionary co mmittee but, under

the Terror, barely escaped the guillotine (the death of Robespierre

spared him). At the École Normale Supérieure, Lagrange and

Laplace were hi s teachers. He obt ained a position at the Éc ol e

Centrale de Travaux Publics, then was a professor at th e École

Polytechnique. He participated in Napoléon’s Egyptian expedi-

tion, was prefect of the Isère, and then studied the theory of heat

propagation, which led him to the expansion of periodic func-

tions.

☞ Second question: does the sequence of partial sums ( f

)

n∈N

converge

pointwise to f ?

In the general case, the answer is unfortunately negative. To obtain a

convergence result, additional assumptions of regular ity of required on f .

In practice, the result which follows will be the most important.

DEFINITION 9.45 (Regularized function) Let f be a function which admits

a limit on the left and on the right at any point. The regularized function

associated to f is the function

∗

: x 7−→

f (x

) + f (x

−

)

THEOREM 9.46 (Dirichl et) Let f ∈ L

[0, a] and let t

∈ [0, a]. If both the

limits on the left and on the right f (t

−

) and f (t

) and the limits on the left and

on the right f

′

−

) a nd f

′

) exist, then the sequence of partial sums



)



n∈N

converges to the regularized value of f at t

, that is, we have

lim

n→∞

) =

f (t

) + f (t

−

)

= f

∗

Notice that not only the function itself, b ut also its derivative, must have a

certain regularity.

It is possible to weaken the ass umptions of this theorem, and to ask only

that f be of bounded variation [37]. In practice, Dirichlet’s theorem is sufﬁ-

cient. Sidebar 4 (page 276) gives an illustration of this theorem.

Fourier series expansion 269

9.4.e Uniform convergen ce of the Fourier series

☞ Third question: is th ere uniform convergence of the sequence of partial

sums ( f

)

n∈N

to f ?

A positive answer holds in t he case of continuous functions w hich are

piecewise of C

class

THEOREM 9.47 Let f : R → C be a continuous periodic function, such that the

derivative of f exists except at ﬁnitely many points, and moreover f

′

is piecewise

continuous. Then we have:

i) the sequence of partial sums ( f

)

n∈N

converges uniformly to f on R;

ii) the Fourier series of f

′

is obtained by differentiating termwise the Fourier series

of f , that is, we have c

( f

′

) = 2iπn c

( f ) for any n ∈ Z;

iii)

+∞

n=−∞



( f )



< +∞.

If f is not continuous, uniform convergence may not be true (even if the

Fourier series converges pointwise); this is the Gibbs phenomenon, describ ed

in more detail below.

☞ Fourth question: what link is there between the regularity of f and the

speed of decay of the Fourier coefﬁcients to 0?

(a) We know already that for f ∈ L

[0, a] , we have c

→ 0 (Riemann-

Lebesgue lemma).

(b) Moreover, if f ∈ L

[0, a] , then

+∞

n=−∞

< +∞ (by Hilber t s pace

theory).

[0, a] , then

+∞

n=−∞

| < +∞, which

is an even stronger result.

(d) It is also possible to show that if f is of C

k−1

class on R and piecewise

of C

class, t hen c

( f

(k)

) = (2πin/a)

( f ) and therefore c

= o(1/n

Moreover, the following equivalence holds:

f ∈ C

∞

[0, a] ⇐⇒ c

= o(1/n

) for any k ∈ N.

Remark 9.48 It is not sufﬁcient for this last result that f be of C

class on [0, a]: it

is indeed required that the graph of f in the neighborhood of 0 “g l u es” nicely with

that in the neighborhood of a.

Remark 9.49 It has been proved (the Carleson-Hunt theorem) that the Fourier series of a

function f which is in L

for some p > 1 converges almost everywhere to f . It is also known

(due to Kolmogorov) that the Fourier series of an integrable function may diverge everywhere.

The settting of L

functions is the only “natural” one for the study of Fourier series.

To look for simple (or u niform) convergence is not entirely natural, then. This is why other

expansions, such as those provided by wavelets, are sometimes required.

270 Hilbert spaces; Fourier series

Remark 9.50 Altho u gh many physics courses introduce Fourier analysis as a wonderful instru-

ment for the study of sound (music par ticularly), it should be noted t h at the expansion in

harmonics of a sound with given pitch (from which Ohm postulated that the “timber” of the

sound could be obtained) is not sufﬁcient, at least if only the amplitudes |c

| of th e harmonics

are considered. The phases of the various harmonics p l ay an important part in the timber

of an instrument. A sound recording played in reverse does not give a recognizable sound,

although the power spectrum is identical [25].

9.4.f The Gib bs phenomenon

On the ﬁgures of Sideb ar 4 on page 276, we can see that the partial Fourier

sums, although converging pointwise to the s quare wave function, do not con-

verge uniformly. Indeed , there always exists a “crest” close to t he discontinuity.

It is possible to show that

• this crest get always narrower;

• it gets closer to the discontinuity;

• its height is consta nt (roughly 8% of t he jump of th e function).

An explanation of this phenomenon will be given in the chapter concerning

the Fourier transform, page 311.

EXERCISES

 Exercise 9.2 Let f , g : R → C be two continuous functions which are 2π-periodic. Denote

by h th e convolution product of f and g, deﬁned by

h(x) = [ f ∗ g](x)

def

2π

f (x − t) g(t) dt.

i) Show that h is a 2π-periodic continuous function. Compute the Fourier coefﬁcients

of h in terms of those of f and g.

ii) Fix the second argument g. Determine the eigenvalues and eigenvectors of the linear

application f 7→ f ∗ g.

 Exercise 9.3 Show that

|sin x| =

∞

n=1

sin

−1

for all x ∈ R.

 Exercise 9.4 (Fej

er sums) The goal of this exercise i s to indicate a way to improve the rep-

resentation of a function by its Fourier series when th e conditio ns of Dirichlet’s theorem are

not valid.

Let f : R → C be 2π-periodic and integrable on [0, 2π]. Deﬁne

f (x) =

k=−n

ikx

, where c

2π

−π

f (x) e

−ikx

dx.

Exercises 271

The Fejér sum of order n of f is the function

f =

f + ··· + S

n−1

f ),

that is, the Cesàro mean of the n ﬁrst Fourier partial sums.

i) Show that

f (x) =

−π

f (x − u) D

(u) du and σ

f (x) =

−π

f (x − u) Φ

(u) du,

where

(u) =

2π

sin



n +



sin u/2

and Φ

(u) =

2nπ



sin nu/2

sin u/2



which are respectively called the Dirichlet kerne l and the Fejér kernel.

ii) Show that the sequence (Φ

)

n∈N

, restricted to [−π, π], is a Dirac sequence.

iii) Deduce from this Fejér’s theorem:

if f is continuous, the sequence (σ

f )

n∈N

converges

uniformly to f ; if f merely admits right and left limits at any point, then the sequence (σ

f )

n∈N

converges to the regularized function associated to f .

Remark: the positivity of the Fejér kernel explains the weaker assumptions of Fejér’s

Theorem, c ompared with Theorem 9.47 (where assumptions concerning th e derivative

are required).

 Exercise 9.5 (Poisson summation formula) Let f be a function of C

class on R, such that

lim

±∞

f (x) = lim

±∞

′

(x) = 0.

Show that the Poisson summation formula

+∞

n=−∞

f (n) =

+∞

n=−∞

+∞

−∞

2πinx

f (x) dx

holds.

Hint: Deﬁne F (x) =

n∈Z

f (x + n) and show that F is deﬁned, 1-periodic, and of C

class. Compute the Fourier coefﬁcients of F and compare them with the values st ated.

This identity will be proved in a more general situati on, using the Fourier transforms of

distributions (Theorem 11.22 on page 309).

PROBLEM

 Problem 4 (Isoperimetric inequality)

➀ Let u : R → C be a function of C

class which is periodic of period L. Show that



u(x)



dx ¶

4π



′

(x)



dx +



u(x) dx



Determine the cases where equality holds.

Lipót Fejér (1880—1959), Hungarian math ematician, was professor at the University of

Budapest. He worked in particular on Fourier seri es, a subject with a bad reputati o n at the

time because it did not conform to the standards of rigor that Cauchy and Wei erstrass had

imposed. For an interesting historical survey of Fejér’s theo rem and other works of this period,

see [54], which also explores the theory of wavelets, one of the modern developments of

harmonic analysis.

272 Hilbert spaces; Fourier series

➁ Let γ be a simple closed path of C

class in the complex p lane, L its length , and A

the area of the region it encloses. Show, using the previous question, that

¾ 4πA ,

with equality if and only if γ is a circle.

Hint: Use the complex Green formula (which states that

∂S

F (z, ¯z) dz = 2i

∂F

∂¯z

for any function F continuous with respect to z and ¯z and admitting continous

partial derivatives with respect to x and y) to show that if γ is parameterized by the

map f : [0, L] → C, with f = u + iv and |f

′

= u

′

+ v

′

= 1, then the area is equal

A =

u(s) v

′

(s) ds.

SOLUTIONS

 Solution of exercise 9 .2. Using Fubini’s theorem, we compute

(h) =

4π

2π



2π

f (x − t) g(t) dt



−inx

4π

2π



2π

f (x − t) e

−in(x−t)



g(t) e

−int

= c

( f ) c

(g).

For an eigenvector f , the coefﬁcients c

( f ) must therefore satisfy

( f ) c

(g) = λc

( f )

for any n ∈ N.

The set of the eigenvalues of f 7→ f ∗ g is exactly the set of the c

(g)’s. Let λ be an

eigenvalue and let I ⊂ N be the set of indices n such that c

(g) = λ; then the eigenfunctions

are t he nonzero functions of the kind

n∈I

inx

 Solution of exercise 9 .3. The function x 7→ |sin x| is even and 2π-périodic; computing it s

Fourier coe fﬁcients (only those involving cosines being nonzero) yields

|sin x| =

∞

n=1



2n + 1

−

2n −1



cos 2nx

after a few lines of calculations. Expanding cos 2θ = 1 −2 sin

θ and noticing that

∞

n=1



2n + 1

−

2n −1



= −1,

it follows that

|sin x| =

∞

n=1

sin

(2n + 1)(2n − 1)

∞

n=1

sin

−1

Note that Dirichlet’s theo rem ensures the pointwise convergence of the series (to the value

|sin x|) at any point x ∈ R. This convergence is moreover uniform.

Solutions of exercises 273

 Solution of exercise 9 .4

i) It sufﬁces to write

(u) =

2π

k=−n

−iku

and to compute this geometric sum. Si milarly, we have

(u) =

n−1

k=0

(u) =

n−1

k=0

2π

Im exp i



n +



sin u/2

and evaluating the geometric sum gives the stated formula.

ii) A direct calculati o n shows that

−π

= 1 and so

−π

= 1.

Let δ > 0 be given. Then for any u ∈ [δ, π], we have sin u/2 ¾ sin δ/2, hence

0 ¶ Φ

(u) ¶

2nπ

sin

δ/2

∀u ∈ [−π, −δ] ∪[δ, π] ,

and this upper bound tends to 0 as [n → ∞]; this shows that [−π, −δ] ∪ [δ, π]

converges uniformly to 0 and proves therefore that (Φ

)

n∈N

(restricted to [−π, π]) is a

Dirac sequence.

iii) The sequence (Φ

)

n∈N

∗

converges weakly to δ in D

′

, and so the sequence (Φ

∗ f )

converges uniformly to f by Theorem 8.22 whenever f is continuous; if f has limits

on the right and left, it converges pointwise to the associated regularized function.

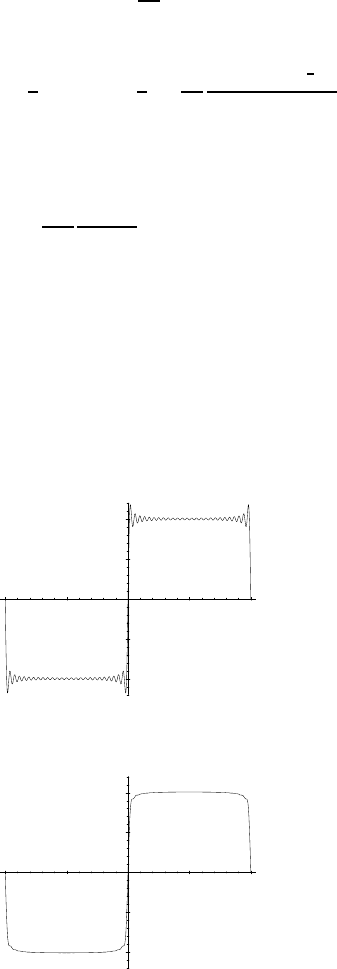
The use of Fejér sums resolves the Gibbs phenomenon close to the discontinuities. The

convergence is not uniform, yet it is much more regular, as shows by the ﬁgure below, which

represents the Fourier partial sums and th e Fejér partial sums of order 25 for the square wave:

−0,5

0,5

−1

−0,5 0,5

−1

−0,5

0,5

−1

−0,5 0,5

274 Hilbert spaces; Fourier series

One can show [24] that for f ∈ L

[0, 2π], the sequence (σ

f )

n∈N

converges to f in L

that is, we have

lim

n→∞

2π



f (t) − f (t)



dt = 0.

 Solution of exercise 9 .5. We compute

+∞

−∞

f (x) e

2πi p x

dx =

n∈Z

n+1

f (x) e

−2πi p x

n∈Z

f (x + n) e

−2πi p(x+n)

dx =

n∈Z

f (x + n) e

−2πi p x

n∈Z

f (x + n) e

−2πi p x

dx =

F (x) e

−2πi p x

dx = c

(F ),

where F (x) =

n∈Z

f (x + p), which is well-deﬁned because of the assumption f (x) =

x→±∞

(1/x

), and w h ere the interversion o f the sum and integral are justiﬁed by the normal

convergence of the series deﬁning F on any compact set.

Moreover, one notes that F is of C

class (because the series converges normally on any

compact set) and it c an be differentiated termwise because of the co ndition f

′

(x) = o(1/x

which implies the normal convergence of the series of derivatives.

Since F is of C

class and obviously is 1-periodic, the Fourier series converges normally. In

partic u l ar,

F (0) =

n∈Z

f (n) =

p∈Z

(F ) =

p∈Z

+∞

−∞

f (x) e

2πi p x

dx.

 Solution of problem 4. Denote by c

the Fourier c oefﬁcients of the function u.

➀ By Parseval’s identity, we have



u(x)



dx =

+∞

n=−∞

+∞

n=−∞



u(x)e

−2πinx/L



and hence



u(x)



dx =



u(x) dx



+∞

n=−∞

n6=0



u(x) e

−2πinx/L



u(x) dx



4π

+∞

n=−∞

n6=0



′

(x) e

−2πinx/L



by integration by parts. But, in t h e last sum, we have n

¾ 1, hence the inequality

+∞

n=−∞

n6=0



′

(x) e

−2πinx/L



+∞

n=−∞



′

(x) e

−2πinx/L



′

(x)|

dx.

This proves the formula stated.

Since all the terms of t h e last sum are non-negative, equality can hold only if all

the terms other than n = 1 or n = −1 are zero, wh ich means only if u

′

(x) is a l inear

combination of e

2πi x/L

and e

−2πi x/L

Solutions of exercises 275

➁ The path being p arameterized by the functions u(s) and v(s), the integration element

dz can be written

dz =



′

(s) + iv

′

(s)



ds.

Take the funct ion F (z, ¯z) = ¯z to apply the Green formula. The area of the surface

S enclosed by the path γ = ∂ S is

2iA = 2 i

∂F

∂¯z

dS =

¯z dz =

(u −iv)(u

′

+ iv

′

) ds

(uu

′

+ vv

′

) ds −i

′

ds + i

′

ds.

The integrand in the ﬁrst term is the derivative of

+ v

); since u(0) = u(L) and

v(0) = v(L), this ﬁrst integral is therefore zero.

The second integral can be integrated by parts, whic h yields

′

ds = −

′

(the boundary term vanishes) and proves that

A =

u(s) v

′

(s) ds.

For any a 6= 0, we have (au − v

′

/a)

¾ 0, hence the inequality a

+ v

′2

¾ 2uv

′

and therefore

A ¶

ds +

′2

ds.

Now use the inequality proved in ➀, making the assumption that

u ds = 0

(translating the path on the real axis if need be, which does not change the area); it

follows that

A ¶

4π

′

(s)

ds +

′

(s)

It sufﬁce s now to ﬁx a so that t h e c oefﬁcients in front of the integrals are equal, which

means a

= 2π/L; with this value, we get

A ¶

4π

′2

+ v

′2

) ds =

4π

Equality holds if au = v

′

/a, which means v

′

= 2πu/L. Together with the relation

′2

+ v

′2

= 1, this implies u(s) =

2π

cos(2πs/L + ϕ) and v(s) =

2π

sin(2πs/L + ϕ),

with ϕ ∈ R, which is, indeed, the equation of a circle with circumference L.

Note that this result, which is rath er intuitive, is by no means easy to prove!

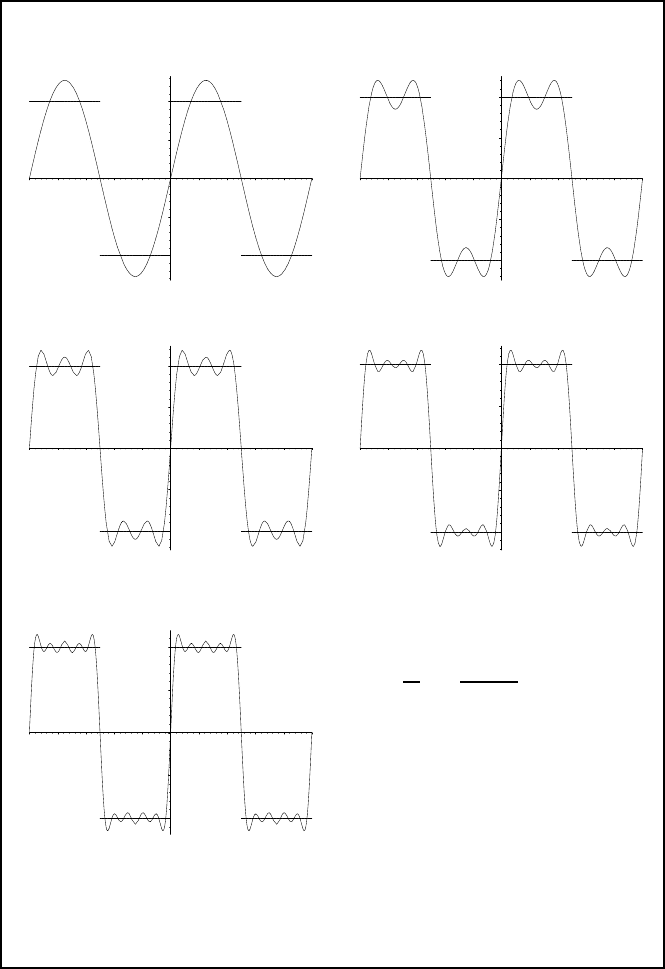
276 Hilbert spaces; Fourier series

Sidebar 4 (Pointwise convergence and Gibbs phenomenon)

–1

–0.5

0.5

–1 1

–1

–0.5

0.5

–1 1

–1

–0.5

0.5

–1 1

–1

–0.5

0.5

–1 1

–1

–0.5

0.5

–1 1

The partial Fourier su ms for the square

wave, with 1, . . . , 5 terms:

(t) =

n−1

k=0

2k + 1

sin(2k + 1)πt.

The pointwise convergence at any point

of continuity is visible, but, close to the

discontinuities, it is clear that the con-

vergence is numerically very bad: there

always remains a “crest,” getting closer

to the discontinuity, with constant ampli-

tude. This is the Gibbs Phenomenon,

ﬁrst exp lained by Josiah Gibbs [39, 40].