Appel W. Mathematics for Physics and Physicists
Подождите немного. Документ загружается.

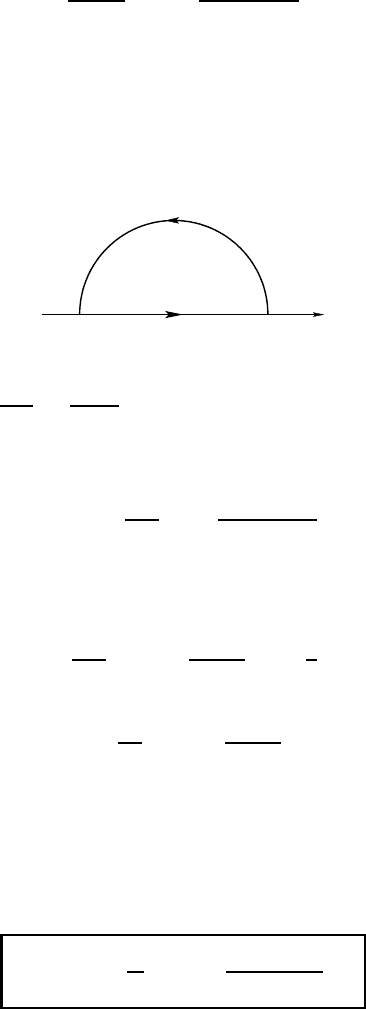
Cauchy principal value 227
Notice — and this will be convenient in certain computations — that
pv
1
x − x
0
= Re
1
x − x
0
±iǫ
.
8.1.d Kramers-Kronig relations
Let F be a function from C into C which is meromorphic on C but holomor-
phic on the closed upper half-plane, which means that all the poles of F have
strictly negative imaginary part. Consider now the contour C described below,
with an arbitrarily large radius:
From Cauchy’s formula, we have
1
2πi
Z
C
F (ζ )
ζ − z
dζ =
¨
F (z) if Im(z) > 0,
0 if Im(z) < 0.
In this formula, put z = x + iǫ with x ∈ R and ǫ > 0:
F (x + iǫ) =
1
2πi
Z
+∞
−∞
F (x
′
)
x
′
− x −iǫ
dx
′
.
Assume that th e integral on the half-circle tends to 0 when the radius tends to
infinity. By letting ǫ tend to 0, and by continuity of F , the preceding results
lead to
F (x) =
1
2πi
pv
Z
+∞
−∞
F (x
′
)
x
′
− x
dx
′
+
1
2
F (x),
hence
F (x) =
1
iπ
pv
Z
+∞
−∞
F (x
′
)
x
′
− x
dx
′
.
This equation concerning F becomes much more interesting by taking succes-
sively its real and imaginary parts; the following theorem then follows:
THEOREM 8.2 (Kramers-Kronig relations) Let F : C → C be a meromorp hic
function on C, holomor phic in the u pper half-plane and going to 0 sufficiently fast at
infinity in this upper half-plane. Then we have
Re
F (x)
=
1
π
pv
Z
+∞
−∞
Im
F (x
′
)
x
′
− x
dx
′

228 Distributions II
and Im
F (x)
= −
1
π
pv
Z
+∞
−∞
Re
F (x
′
)
x
′
− x
dx
′
These are called dispersion relations and a re very useful in optics (s ee, e.g., the
book by Born and Wolf [14, Cha pter 10]) and in statistical physics. Physicists
call these formulas the Kramers-Kronig relations,
1
while mathematicians say
that Re(F ) is the Hilbert transform of Im(F ).
Remark 8.3 If F is meromorphic on C and holomorphic in the lower h al f-plane (all its poles
have positi ve imaginary parts), then it satisfies relations which are dual to those just proved
(also called Kramers-Kronig relations, w h ich does not simplify matters):
Re
F (x)
= −
1
π
pv
Z
+∞
−∞
Im
F (x
′
)
x
′
− x
dx
′
and Im
F (x)
=
1
π
pv
Z
+∞
−∞
Re
F (x
′
)
x
′
− x
dx
′
.
We will see, in Chapter 13, that the Fourier transform of causal functions t 7→ f (t) (those
that vanish for negative values of the variable t), when it exists, sat isfies the Kramers-Kronig
relations of Theorem 8.2.
Remark 8.4 What happens i f F is holomorphic on both the upper and the lower half-plane?
Since it is assumed that F has no pole on the real axis, it i s then an entire function. The
assumption that the integ ral on a circle tends to zero as the radius gets large then leads (by the
mean value property) to the vanishing of the function F , which is the only way to reconcile
the previous formulas wit h t h o se of Theorem 8.2.
Remark 8.5 In electromagnetism, the electric induction D and the electric field E are linked,
for a monochromatic wave, by
D( x, ω) = ǫ(ω) E( x, ω),
where ǫ(ω) is the dielectric constant of the material, depending on the pulsation ω of the
waves. This relation can be rewritten (via a Fourier tranform) i n an integral relation between
D( x, t) and E( x, t):
D( x, t) = E( x, t) +
Z
+∞
−∞
G(τ) E( x, t −τ) dτ,
where G(τ) is the Fourier transform of ǫ(ω) −1. In fact, since the ele ctric field is the physical
field and the field D is derived from it, the previous relation must be c au sal, that is, G(τ) = 0
for any τ < 0. One of the main consequences is that the function ω 7→ ǫ(ω) is analytic in the
lower half-plane of the complex plane (see Chapter 12 on the Laplace transform). From the
Kramers-Kronig relations, interesting information concerning the function ω 7→ ǫ(ω) can be
deduced. Thus, if the plasma frequency is defined by ω
p
2
= lim
ω→∞
ω
2
[1 − ǫ(ω)], we obtain
the sum rule
ω
p
2
=
2
π
Z
+∞
0
ω Im
ǫ(ω)
dω.
The reader is invited to read, for instance, the book by Jackson [50 , Chapter 7.10] for a more
detailed presentation of this sum rule.
1
Dispersion relations first appeared in physics in the study of the dielectric constant of
materials by R. de L. Kronig in 1926 and, independently, in the theory of scattering of light
by atoms by H. A. Kramers in 1927.
Cauchy principal value 229
Exercise 8.1 Using the Kramers-Kronig relations, show that
Z
+∞
0
sin x
x
dx =
π
2
.
(Solution page 245)
8.1.e A few equations in the sense of d istributions
Recall (Theorem 7.28 on page 191) that the solutions of the equation x·T (x) =
0 are the multiples of δ.
PROPOSITION 8.6 We have x ·pv
1
x
= 1 (where 1 is the constant function x 7→ 1).
Proof. Indeed, for any test function ϕ ∈ D(R), we have by definition of the product
of a distribution (pv
1
x
) by a C
∞
function:
x pv
1
x
, ϕ
·
=
pv
1
x
, xϕ
·
= lim
ǫ→0
+
Z
|x|>ǫ
x ϕ(x)
x
dx =
Z
+∞
−∞
ϕ(x) dx = 〈1, ϕ〉.
THEOREM 8.7 (Solutions of x · T ( x) = 1) The solutions, in the space of distribu-
tions, of the equation
x · T (x) = 1,
are the distributions given by T (x) = pv
1
x
+ αδ, with α ∈ C.
Proof. If T satisfies x · T (x) = 1, t h en S = T −p v(1/x) satisfies x · S (x) = 0 and
thus, according to Theorem 7.28 on page 191, S is a multiple of δ.
Theorem 7.28 generalizes as follows:
PROPOSITION 8.8 Let n ∈ N. The solutions of equation x
n
· T (x) = 0 are the
linear combinations of δ, δ
′
, . . . , δ
n−1
.
Let f be a function continuous on R, with isolated zeros. For ea ch such
zero x
i
of f , we s ay that x
i
is of multiplicity m if there exists a continuous
function g, which does not vanish in a neighborhood of x
i
, such that f (x) =
x
m
g(x) for x ∈ R.
If f ha s only isolated zeros with finite multiplicity, then one can treat the
equation f (x) · T (x) = 0 locally around each zero in the same manner as
x
m
T (x) = 0.
THEOREM 8.9 (Solutions of f ( x) · T ( x) = 0) Let f be a continuous fu nction
on R. Denote by Z( f ) = {x
i
i ∈ E} the set of its zeros, and assume these zeros
are isolated and with finite multiplicities m
i
.
The distributions solutions to the equation f (x) · T (x) = 0 are given by
T (x) =
X
i∈I
m
i
−1
X
k=0
α
i,k
δ
(k)
(x − x
i
),
where α
i,k
are arbitrary complex numbers.

230 Distributions II
Example 8.10 The equation sin x · T (x) = 0 has for solutions the distributions o f the form
P
n∈Z
α
n
δ(x −nπ).
The equation (cos x −1) · T (x) = 0 has for solutions the distributions of the form
P
n∈Z
α
n
δ(x −nπ) + β
n
δ
′
(x −nπ)
.
THEOREM 8.11 (Solutions of ( x
2
− a
2
) · T ( x) = 1) Let a > 0 be given. The
distribution solutions of the equation (x
2
−a
2
) · T (x) = 1 are those given by
pv
1
x
2
−a
2
+ α δ(x −a) + β δ(x + a),
where α and β are complex numbers, and where we denote
pv
1
x
2
−a
2
=
1
2a
pv
1
x + a
−pv
1
x − a
.
8.2
Topology in DD
D
D
DD
′
8.2.a Weak convergence in DD
D
D
DD
′
DEFINITION 8.12 A sequence of distributions (T
k
)
k∈N
converges wea kly (or
simply “converges”) in D
′
if, for any test function ϕ ∈ D, the sequence of
complex numbers 〈T
k
, ϕ〉 converges in C. We then denote by 〈T , ϕ〉 this limit,
which defines a linear function T on D, called the weak limit of (T
k
)
k∈N
in D
′
.
THEOREM 8.13 If (T
k
)
k∈N
converges weakly in D
′
to a functional T , then T is
continuous and is therefore a distribution. The weak convergence in D
′
is denoted by
T
k
D
′
−−→ T .
Exercise 8.2 For n ∈ N, let T
n
be the regular distribution associated to the loc al ly integrable
function x 7→ sin(nx). Show that the sequence (T
n
)
n∈N
converges weakly to 0 in D
′
.
THEOREM 8.14 (Continuity of differentiation) The operation of differentiation
in D
′
(R) is a continuous linear operation: if T
k
D
′
−−→ T , then for any m ∈ N, we
have T
(m)
k
D
′
−−→ T
(m)
.
Obviously this extends to partial derivatives of distr ibutions in R
n
.
Topology in D
′
231
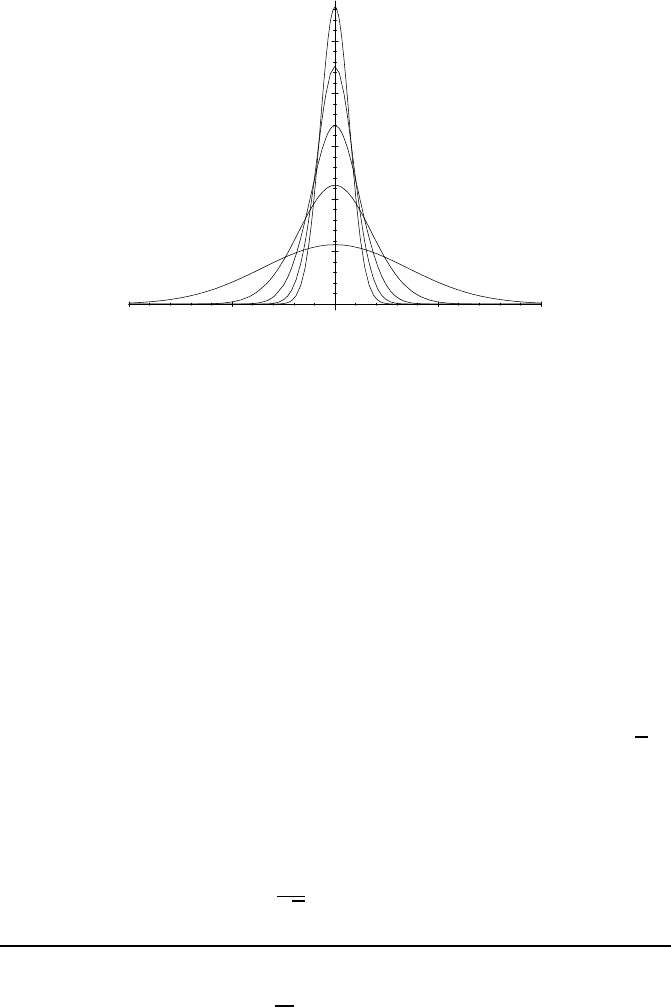
0
1
2
−2
−1 1
2
Fig. 8.3 — The sequence of gaussian functions (g
n
)
n∈N
, for n = 1, . . . ,5.
This theorem is extremely powerful and justifies the interchange of limits
and derivatives, which is of course impossible in the sense of functions.
2
8.2.b Sequences of functions converging to δ
DEFINITION 8.15 A Dirac se quence (of functions) is any sequence of func-
tions f
k
: R → R locally integrable, s uch that
➀ there exists a real number A > 0 such that, for any x ∈ R and any
k ∈ N, we have
|x| ¶ A
=⇒
f
k
(x) ¾ 0
,
➁ for any a ∈ R, a > 0,
Z
|x|¶a
f
k
(x) dx −−−→
k→∞
1 and f
k
(x)
cv.u.
−−→ 0 on a < |x| <
1
a
.
Example 8.16 An e xample of a Dirac sequence is the sequence ( f
n
)
n∈N
defined by f
n
(x) =
nΠ(nx) for any x ∈ R and any n ∈ N. (Check this on a drawing.)
Example 8.17 The sequence of functions (g
n
)
n∈N
defined by
g
n
(x)
def
=
n
p
π
e
−n
2
x
2
for x ∈ R
2
Consider, for instance, the sequence of functions ( f
n
)
n∈N
defined by
f
n
(t) =
n
X
k=1
1
2k
cos 2kt for any t ∈ R.
The functions f
n
are all differentiable, but their limit f is a “sawtooth” function, which is not
differentiable at the points of the form nπ with n ∈ Z.

232 Distributions II
0
1
3
4
5
−2
−1 1
2
Fig. 8.4 — The sequence of fu nct ions ψ
n
(x) =
sin
2
(πnx)
nπ
2
x
2
for n = 1 to 5.
is a Dirac sequence (see Figure 8.3 on the previous page).
THEOREM 8.18 Any Dirac sequence converges weakly to the Dirac distribution δ
in D
′
(R).
Proof. See Appendix D.
Example 8.19 Similarly, the sequence of functions (ψ
n
)
n∈N
defined by
ψ
n
(x) =
sin
2
(πnx)
nπ
2
x
2
for x ∈ R
is a Dirac sequence (see Figure 8.4) and thus converges also to δ.
Remark 8.20 Without the positivit y assumption for x close to 0, there is nothing to prevent
contributions proportional to δ
′
to arise in the limit! Thus, consider the sequence of functions
(k
n
)
n∈N
given by the graph
n
2
−n
2
−
1
n
1
n
It is easy to show that k
n
D
′
−−→ δ
′
. Let ( f
n
)
n∈N
be a Dirac sequence; then the sequence
( f
n
+ k
n
)
n∈N
, which still satisfies ➁, but not ➀, converges to δ + δ
′
and not to δ.
Topology in D
′
233
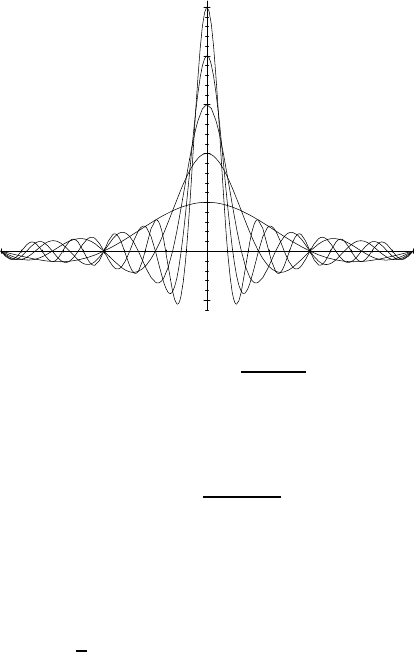
−2
0
2
4
6
8
10
−1
−0,5 0,5
1
Fig. 8.5 — The functions b
n
: x 7−→
sin 2πnx
πx
, for n = 1, . . . ,5.
Consider now the sequence of functions
b
n
(x) =
sin 2πnx
πx
.
All the functions b
n
share a common “envelope” x 7→ 1/πx and the sequence
of real numbers (b
n
(x))
n∈N
does not converge if x /∈ Z (see Figure 8.5). We do
have b
n
(0) → ∞, but , for instance,
b
n
1
4
=
¨
(−1)
k
/2π if n = 2k + 1,
0 if n = 2k.
In particular, this sequence (b
n
)
n∈N
is not a Dirac sequence. Yet, despite this
we have the following result:
PROPOSITION 8.21 The sequence (b
n
)
n∈N
converges to δ in the sense of distribu-
tions.
How to e xplain t his ph enomenon?
Proving the convergence of (b
n
)
n∈N
to δ is, b ecaus e of the lack of pos-
itivity, harder than for a Dirac sequence. In the case that concerns us, the
sequence of functions (b
n
)
n∈N
exhibits ever faster oscillations wh en we let n
tend to infinity (see Figure 8.5), and, after getting rid of t he singularity at 0,
we can hope to be able to invoke the Riemann-Lebesgue lemma (see Theo-
rem 9.44). Moreover, it is easy to compute that
R
b
n
= 1 for all n ∈ N
∗
(for
example, by the method of residues).
Proof of Proposition 8.21. Let ϕ ∈ D be a test function and let [−M, M] be an
interval containing the support of ϕ.

234 Distributions II
We can always write ϕ(x) = ϕ(0) + x ψ(x), where ψ if of C
∞
class. Then we have
〈b
n
, ϕ〉 = ϕ(0)
Z
M
−M
sin 2πnx
πx
dx +
Z
M
−M
ψ(x) sin(2πnx) dx,
and the first integral, via the substitution y = nx, tends to the improper integral
Z
+∞
−∞
sin πx
πx
dx = 1 ,
whereas the second integral tends to 0, by the Riemann-Lebesgue lemma.
Finally, t he convergence to δ is highly useful because of the following
theorem:
THEOREM 8.22 Let ( f
n
)
n∈N
be a Dirac sequence of functions. If g is a bounded
continuous function on R, then f
n
∗g exists for all n ∈ N and the sequence ( f
n
∗g)
n∈N
converges uniformly to g.
If g is not continuous but the limits on the left or the right of g exist at the point x,
then f
n
∗ g(x) tends to
1
2
g(x
−
) + g(x
+
)
.
8.2.c Convergence in DD
D
D
DD
′
and c onvergence
in the sense of functions
The previous examples show that a sequence ( f
n
)
n∈N
of regular distributions
may very well converge in D
′
to a regular distribution f without converging
pointwise almost everywhere (and even more wit hout converging uniformly)
in the sense of functions. I n particular, the Riemann-Lebesgue lemma is
equivalent to the following proposition:
PROPOSITION 8.23 The sequence of regular distributions ( f
n
)
n∈N
defined by the
functions f
n
: x 7→ sin(nx) converges to 0 in D
′
, but it converges pointwise only for
x ∈ πZ.
8.2.d Regularization of a distribution
What happens w hen we take the convolution of a function f of C
1
class
with a function g of C
2
class? Assuming that this convolution exists and
denoting h = f ∗ g, the function h will be infinitely differentiable in the sense
of distributions, but how many times will it be differentiable in the sense of
functions?
Compute the derivative. It is possible to write h
′
= f
′
∗ g and, since f
′
and g are f unctions, h
′
is well-defined in the sense of functions. Continue. It
is not possible to differentiate f more than that, but g is still available, and
so h
′′
= f
′
∗ g
′
is still a function, as is the third derivative h
′′′
= f
′
∗ g
′′
. But
going farther is not possible.
Similarly, the convolution of a f unction of C
k
class with a function of C
ℓ
class will produce a function of C
k+ℓ
class.
Topology in D
′
235
These results generalize to distributions. Of course, it is not reasonable
to speak of “C
∞
class” (since distributions are always infinitely differentiable
anyway). But “regularity” for a distribution consists precisely in being what
is called a “regular distribution,” namely, a distr ibution associated to a locally
integrable function.
An interesting result (wh ich is, in fact, quite intuitive) is that the con-
volution by a C
∞
function “smoothes” the object which is sub ject to the
convolution: the result is a function which is C
∞
. This is th e ca se also if
we take the convolution of a distribution with a C
∞
function: the result is
a regular distribution associated to a function, and in certain cases one ca n
show th at the result is also C
∞
.
THEOREM 8.24 (Regularization of a distribution) Let T ∈ D
′
be a distribution
and ψ ∈ C
∞
(R), and assume that T ∗ψ exists. Then T ∗ψ is a regular distribution
associated to a func tion f , which is given by
f (x) = T ∗ψ(x) =
T (t), ψ(x − t)
.
Let T ∈ D
′
and ϕ ∈ D (so ϕ is now not only of C
∞
class, but also with
bounded support). Then T ∗ ϕ exists and is a regular distribution associated to a
function g of C
∞
class, with derivatives given by the formula
g
(k)
(x) =
T (t), ϕ
(k)
(x − t)
.
8.2.e Continuity of convolution
The following theorem shows that the operation of convolution with a fixed
distribution is continuous for the weak topology on D
′
:
THEOREM 8.25 (Continuity of convolution) Let T ∈ D
′
. If (S
k
)
k∈N
converges
weakly in D
′
to T , and if moreover all the S
k
are su pported in a fixed closed subset
such that all the S
k
∗ T exist, then the sequence (S
k
∗ T ) converges in D
′
to S ∗ T .
Consider now a Dirac sequence (γ
n
)
n∈N
, with elements belonging to D.
It converges weakly to δ in D
′
(this is Theorem 8.18); moreover, we know
(Theorem 8.24) that if T is a distribution, we have γ
n
∗ T ∈ C
∞
(R). Since
γ
n
∗ T −−−→
n→∞
T , we deduce:
THEOREM 8.26 (Density of DD
D
D
DD in DD
D
D
DD
′
) Any distribution T ∈ D
′
is the limit in
D
′
of a sequence of f unctions in D. One says that D is dense in D
′
.
In ot her words, any d istribution is the weak limit of a sequence of func-
tions of C
∞
class with bounded support.
Exercise 8.3 Find a sequence (ϕ
n
)
n∈N
in D which converges weakly to X in D
′
.
(See Exercise 8.11 on page 242)

236 Distributions II
8.3
Convolution algebras
DEFINITION 8.27 A convolution algebra is any vector space of distributions
containing the Dirac distribution δ and for which the convolution product
of an arbitrary number of factors is defined.
There are two well-known and very important examples.
THEOREM 8.28 (EE
E
E
EE
′
, DD
D
D
DD
′
+
and DD
D
D
DD
′
−
) The space E
′
of distributions with bounded sup-
port is a convolution algebra.
The space of distributions with support bounded on the left, denoted DD
D
D
DD
′
+
and
the space of distributions with support bounded on the right, denoted DD
D
D
DD
′
−
, are also
convolution algebras.
These algebras, as the name indicates, provide means of solving certain
equations by means of algebraic manipulations. In particular, many physical
problems can be put in the form of a convolution equation of the type
A ∗ X = B
where A and B are distributions (B is often called the “ source”) and the
unknown X is a d istribution.
3
The problem is to find a solution and to
determine if it is unique. So we are, quite naturally, led to the search for a
distribution denoted A
∗−1
, which is called the convolution inverse of A or,
sometimes, Green function of A, which will be such th at
A ∗ A
∗−1
= A
∗−1
∗ A = δ.
Remark 8.29 This inverse, if it exists, is unique in the algebra under consideration. Indeed, suppose
there exist, in a same algebra, two distributions A
′
and A
′′
such that
A ∗ A
′
= A
′
∗ A = δ and A ∗ A
′′
= A
′′
∗ A = δ.
Then
A
′′
= A
′′
∗δ = A
′′
∗(A ∗ A
′
) = (A
′′
∗ A) ∗ A
′
= δ ∗ A
′
= A
′
and therefore
A
′′
= A
′
.
3
For instance, notice that any linear differential equation with constant coefficie nts
a
0
+ a
1
d
dt
+ ···+ a
n
d
n
dt
n
X (t) = B(t)
can be reexpressed in the form of a convolution product
a
0
δ + a
1
δ
′
+ ···+ a
n
δ
(n)
∗ X (t) = B(t).
