Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Derivation of a discontinuous func tion 207

Then ap ply directly the formula (7.9), noticing that

〈△f , ϕ〉 =

ZZZ

f △ϕ d



(0)

′

, ϕ



∂ϕ

∂ n



(1)

, ϕ



−∂ f

∂ n

s, 〈{△f }, ϕ〉 =

ZZZ

ϕ △ f d

7.5.d Application: laplacian of 1/ r in 3-s pace

We continue working in R

. If f is a f unction on a subset of R

which is

twice differentiable and radial, its laplacian in the sense of functions can be

computed by the formula

△f =

∂

∂ r

(r f ).

Hence, in the sense of functions, we have △





= 0, except possibly at r = 0.

We now try to compute this laplacian in the sense of d istributions.

For any ǫ > 0, deﬁne

(r) =

1/r for r > ǫ,

0 for r < ǫ.

Then apply the formula

△f = σ

(0)

′

+ σ

(1)

+ {△f }

to the function f

. For this, denote by S

the sphere r = ǫ and by V

the

volume interior to this surface. The jumps of f

and ∂ f

/∂ n accross the

surface S oriented toward the exterior are therefore equal to 1/r and −1/r

respectively. We thus ﬁnd

〈△f

, ϕ〉 =

ZZZ

△ϕ d

r (by deﬁnit ion)

(0)

′

+ σ

(1)

+ {△f

}, ϕ

but {△f } = 0



−

∂ϕ

∂ n



s +

ZZZ



−



ϕ( r) d

Each term in the last expression has a limit as [ǫ → 0], respectively, 0 (since

the derivatives of ϕ are bounded and the surface of integration has area of

order of magnitude ǫ

) and

lim

ǫ→0

ZZZ



−



ϕ( r) d

r = −4π ϕ(0)

by continuity of ϕ (the factor 4π arises as the surface area of S

divided

by ǫ

208 Distributions I

Notice now that



△

, ϕ

ZZZ

△ϕ( r) d

= lim

ǫ→0

ZZZ

( r) △ϕ( r) d

r = lim

ǫ→0

〈△f

, ϕ〉,

since the integrand on the left is an integrable function (because the volume

element is given by r

sin θ dr dθ dϕ). Putting everything together, we ﬁnd

that



△

, ϕ

ZZZ

△ϕ( r) d

r = −4π ϕ(0).

In other words, we have proved the following theorem:

THEOREM 7.54 The laplacian of the radial function f : r 7→

krk

is given by

△





= −4π δ.

It is this equation which, applied to electrostatics, will give us the Poisson

law (see Section 7.6.g on page 216).

In the same manner, one can show that

THEOREM 7.55 In R

, the laplacian of r 7→ log krk is

△



log |r|



= 2π δ. (7.11)

Similarly, one gets (see [81]) :

PROPOSITION 7.56 For n ¾ 3, we have in R

the formula

△



n−2



= −(n −2)S

δ,

where S

is the “area” of the unit sphere in R

, namely

(2π)

n/2

Γ(n/2)

Convolution 209

7.6

Convolution

7.6.a The tensor product of two functions

DEFINITION 7.57 (Tensor product of f unct ions) Let f and g be two func-

tions deﬁned on R. The direct product of f and g (also called the tensor

product) is the function h : R

→ R deﬁned by h(x, y) = f (x) g( y) for any

x, y ∈ R. It will be denoted h = f ⊗ g.

This deﬁnition is generalized in the obvious manner to the product of

f : R

→ C by g : R

→ C.

A somewhat grandiloquent word (tensor product!!) for a very simple thing,

in the end. But despite th e apparent trivia lit y of this notion, the tensor

product of f unctions will be very useful.

Example 7.58 Let Π (x) = 1 for |x| < 1/2 and Π(x) = 0 elsewhere. The tensor product of

the functions H and Π is given by the following graphical representation, where the gray area

corresponds to the points where H ⊗Π takes the value 1, and the white area to those where it

takes the value 0:

H ⊗Π =

−

or H ⊗Π(x, y) = H (x) Π( y).

7.6.b The te nsor product of distributions

Let’s now see how to generalize the tensor product to distributions. For t his,

as usual, we consider the distr ibution associated to the tensor product of two

locally integrable functions. If f : R

→ C and g : R

→ C are locally

integrable, and if we write h : R

p+n

→ C as their tensor product, then for any

test f unction ϕ ∈ D(R

p+n

) we have

〈h, ϕ〉 =



f (x) g( y), ϕ(x, y)



f (x) g( y) ϕ(x, y) dx dy

f (x)

Z

g( y) ϕ(x, y) dy



dx =

f (x),



g( y), ϕ(x, y)



Take now a distribution S(x) on R

and a distribution T ( y) on R

. The

function

x 7→ θ(x)

def



T ( y), ϕ(x, y)



210 Distributions I

is a test function on R

; we can therefore let S a ct on it and, as for regular

distributions, we d eﬁne the distribution S (x) T ( y) by



S(x) T ( y), ϕ(x, y)



def

S(x),



T ( y), ϕ(x, y)



DEFINITION 7.59 (Tensor product of distributions) Let S and T be two dis-

tributions. The direct product, or tensor product, of the distributions S

and T is the distribution S (x) T ( y) deﬁned on the space of test functions on

×R



S(x) T ( y), ϕ(x, y)



def

S(x),



T ( y), ϕ(x, y)



It is denoted S ⊗ T , or S (x) T ( y).

The tensor product is of course not commutative: S ⊗ T 6= T ⊗ S .

Remark 7.60 Be carefull not to mistake S (x) T ( y) with a product of distributions, which is

not well-deﬁned in general (see note 6 on page 190).

Example 7.61 The Dirac distribution in two dimensions can be deﬁned as the direct product

of two Dirac distributions in one dimension:

(2)

( r ) = δ

(2)

(x, y) = δ(x) δ( y).

This can be illustrated graphically as follows:

δ(x)

(2)

(x, y)

δ( y)

Similarly, in three dimensions, we have δ

(3)

( x) = [δ ⊗δ ⊗δ](x, y, z) = δ(x) δ( y) δ(z).

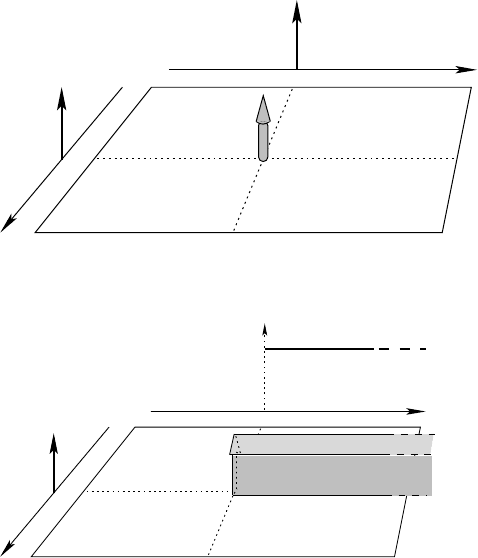
Example 7.62 In the same way, the tensor product δ ⊗ H can be expressed by the graph

δ(x)

δ(x) H ( y)

H ( y)

Convolution 211

This distribution on R

acts on a test function ϕ ∈ D(R

) by



δ(x) H ( y), ϕ(x, y)



+∞

ϕ(0, y) dy.

Caution is that sometimes the constant function is omitted from the no-

tation of a tensor product f ⊗1. For instance, in two dimensions, the distri-

bution denoted δ(x) is in reality equal to δ(x) 1( y) and acts therefore by the

formula



δ(x), ϕ(x, y)





δ(x) 1( y), ϕ(x, y)



+∞

−∞

ϕ(0, y) dy.

This should not be confused with δ( r) = δ(x, y) = δ(x) δ( y).

Example 7.63 (Special relativity) In t h e setting of Sec tion 7.4.e, the density of charge ρ(x) =

q δ

(3)

( x) can also be written

ρ = q 1 ⊗δ

(3)

since



1 ⊗δ

(3)



(c t, x) = 1(c t) δ

(3)

( x) = δ

(3)

( x).

7.6.c Convolution of two functions

DEFINITION 7.64 (Convolution of functions) Let f and g be two locally inte-

grable functions. Their convolution, or convolution product, is the function h

deﬁned by

h(x)

def

f (t) g(x − t) dt,

where this is well-deﬁned. It is denoted

h = f ∗ g

or less rigorously h(x) = f (x) ∗ g(x). Note that t he convolution of two

functions does not always exist.

Example 7.65 The convolution of the Heaviside function with itself is given by

H ∗ H (x) =

+∞

−∞

H (t) H (x − t) dt = x H (x).

Conversely, the convolution of H with x 7→ 1/

|x| is not deﬁned.

 Exercise 7.4 Show t h at the convolution product ∗ is commutative, that is, h = f ∗g = g ∗ f

whenever one of the two convolutions is deﬁned.

 Exercise 7.5 Let a, b ∈ R

be real numbers such that a 6= b. Compute the convolution of

x 7→ e

−|ax|

with x 7→ e

−|b x|

(Solutions page 245)

212 Distributions I

It is possible to interpret graphically the convolution of two functions.

Indeed, d enoting by h = f ⊗ g their tensor product, we have

f ∗ g(x) =

f (t) g(x − t) dt =

h(t, x − t) dt,

which means that one integrates the function h : R

→ C on the path formed

by the line D

with slope −1 passing through the point (0, x).

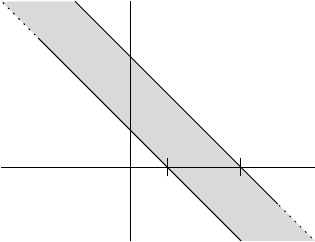
Example 7.66 Let f = Π and g(x) = Π(x −

), where Π is the “rectangle” function (see

page 213). Put h = f ⊗ g and k = f ∗ g. Then the value of k(x) at a point x ∈ R is

given by the integral of h on t h e line D

below. The gray area corresponds to those points

where h(x, y) = 1, and the white area to those where h(x, y) = 0.

0 1

(x, 0)

(0, x)

If the diagonal line D

intersects the support of f ⊗ g in a ﬁnite segment,

then the convolution of f by g is well deﬁned at the point x.

Thanks to this interpretation, we have therefore proved the following re-

sult:

THEOREM 7.67 The convolution ot two locally integrable functions f and g exists

whenever one at least of the following conditions holds:

i) the functions f and g both have bounded support;

ii) the functions f and g are both zero for sufﬁciently large x (they have bounded

support “on the right”);

iii) the functions f and g are both zero for sufﬁciently small (negative) x (they ha ve

bounded support “on the left”).

Those conditions are of course sufﬁcient, but not necessary.

 Exercise 7.6 Show graphically that H ∗H is well deﬁned, but not H ∗

H (where, as deﬁned

previously,

H (x) = H (−x)).

Convolution 213

7.6.d “Fuzzy” measurement

The “rectangle” function Π is d eﬁned by

Π(x) =

(

1 if |x| <

0 if |x| >

Π(x)

−

Let now a > 0 be ﬁxed. Denoting by f

the convolution of f by a similar

rectangle with wid th a and height 1/a, we have

(x) = f (x) ∗





x+a/2

x−a/2

f (t) dt,

which is simply the average of the function f on an inter val around x of

length a. It is then possible to model simply an imperfect measurement of th e

function f , for which the uncertainty is of size a. Then details of siz e ℓ ≪ a

disappear, whereas those of size ℓ ≫ a remain clearly visible.

This model can be reﬁned by convolution of f by a gaussian or a lorentzian

(see Example 279), for instance.

Example 7.68 A spectral ray has the shape of a lorentzian (a classical result of atomic p hysi cs),

but what is observed experimentally is slightly different. Indeed, the atoms of the emitting gas

are not at rest, but their velocities are distributed according to a certain distribution, given by

a “maxwellian” function (this is the name given to the gaussian by physicists, because of the

Maxwell-Boltzmann distribution). Due to the Doppler effect, the wavelengths emitted by the

atoms are shifted by an amount proportional to the speed; therefore the spe ctral distribution

observed is the convolution of the original shape (the lorentzian) by a gaussian, with variance

proportional to the temperature.

It will be seen

that the sequence of functions



nΠ(nx)



n∈N

converges (in

a sense that will be made precise in Deﬁnition 8.12 on page 230) to the Dirac

distribution δ. Thus, it can be expected that, in the limit [n → ∞], since

the convolution does not change anything (the “precision” of measurement is

inﬁnite), we have f ∗δ = f ; thus we expect that δ will be a unit element for

the convolution product.

To show this precisely, we ﬁrst have to extend the convolution ∗ to the

setting of distributions.

See Exercise 8.12 on page 242.

214 Distributions I

7.6.e Convolution of dis tributions

By the same method as before, we wish to extend th e convolution product

to distributions, so that it coincides with the convolution of functions in

the case of regular distributions. Now, for two locally integrable functions f

and g (such th at the convolution f ∗g is deﬁned), we have for any ϕ ∈ D(R):

〈f ∗ g, ϕ〉 =

( f ∗ g)(t) ϕ(t) dt

ϕ(t)

Z

f (s) g(t − s) ds



f (x) g( y) ϕ(x + y) dx dy (x = s, y = t − s)



f (x) g( y), ϕ(x + y)



since the jacobian in this change of variable is equal to | J | = 1.

DEFINITION 7.69 (Convolution of distributions) Let S a nd T be two distri-

butions. The convolution of S and T is deﬁned by its action on any test

function ϕ ∈ D given by

〈S ∗ T , ϕ〉

def



S(x) T ( y), ϕ(x + y)



The convolution of distribut ions does not a lways exist! The general condi-

tions for its existence are difﬁcult to write down. However, we may note that,

as in the case of functions, the following result holds:

THEOREM 7.70 The convolution of distributions with support bounded on the left

(resp. bounded on the right) always exists.

The convolution of an arbitrary distribution with a distribution with bounded

support always exists.

Indeed, if x 7→ ϕ(x) is a nonzero test function, the map (x, y) 7→ ϕ(x + y)

does not have b ounded support, that is, it is not a test f unction on R

! If the

support of x 7→ ϕ(x) is a segment [a, b], then the support of (x, y) 7→ ϕ(x+ y)

is a strip as represented below:

Convolution 215

In particular, if we denote by Ω t he support of S and by Ω

′

the support

of T , then the convolution of S and T has a sense if the intersection of

an arbitrary strip of this type with the cartesian product Ω × Ω

′

is always

bounded. The reader can easily check that this condition holds in all the

situations of t he previous theorem.

PROPOSITION 7.71 Let S and T be two distributions. Assume that the convolu-

tion S ∗ T exists. Then T ∗ S exists also and S ∗ T = T ∗ S (commutativity of

the convolution).

Similarly, if S, T and U are three distributions, then

S ∗(T ∗ U ) = (S ∗ T ) ∗ U = S ∗ T ∗ U

if S ∗ T , T ∗ U , and S ∗ U make sense (as sociativity of the convolution product).

Counterexample 7.72 Let 1 denote as usual the constant functio n 1 : x 7→ 1. This function is

locally integrable and therefore deﬁnes a regular distribution, Moreover, the reader can check

that (1 ∗δ

′

) = 0, hence (1 ∗ δ

′

) ∗ H = 0. But, on the oth er hand, ( δ

′

∗ H ) = δ, and hence

1 ∗(δ

′

∗ H ) = 1, which shows that

(1 ∗δ

′

) ∗ H 6= 1 ∗(δ

′

∗ H ).

This can be explained by the fact that 1 ∗ H does not exist.

7.6.f Applications

Let f and g be two integrab le functions. They deﬁne regular distributions,

and, moreover (as easily checked), f ∗ 1 and g ∗ 1 exist and are in fact con-

stant and equal to 1 ∗f =

f (x) dx, 1 ∗g =

g(x) dx, respectively. Assume

moreover that f ∗ g exists. Then, wr iting 1 ∗[ f ∗ g] = [1 ∗f ] ∗ g, we ded uce

the following result:

THEOREM 7.73 Let f and g be tw o integrable functions such that the convolution

of f and g exists. Then w e ha ve

[ f ∗ g](x) dx =

Z

f (x) dx



Z

g(x) dx



Remark 7.74 The convolution product is the continuous equivalent of the Cauchy product of

absolutely convergent series. Recall that the Cauchy product of the series

and

the series

such that

k=0

n−k

By analogy, one may write w = a ∗ b. Then we have

∞

n=0

(a ∗ b)



∞

n=0





∞

n=0



Using the deﬁnition of convolution, it is easy to sh ow the following rela-

tions:

216 Distributions I

THEOREM 7.75 Let T be a distribution. Then we hav e

δ ∗ T = T ∗δ = T .

For any a ∈ R, the translate of T by a can be expressed as the convolution

δ(x − a) ∗ T (x) = T (x) ∗δ(x −a) = T (x − a),

and the derivatives of T can be expressed as

′

∗ T = T ∗δ

′

= T

′

and δ

(m)

∗ T = T ∗δ

(m)

= T

(m)

for any m ∈ N.

Proof

• Let T ∈ D

′

. Then, for any ϕ ∈ D, we have

〈T ∗δ, ϕ〉 =



T (x) δ( y), ϕ(x + y)



T (x) ,



δ( y), ϕ(x + y)





T (x), ϕ(x)



= 〈T , x〉,

which shows that T ∗δ = T . Hence we also have δ ∗ T = T .

• Let a ∈ R. Then

〈T ∗δ

, ϕ〉 =

T (x) ,



δ( y −a), ϕ(x + y)





T (x) , ϕ(x + a)





T (x −a), ϕ(x)



which shows that T ∗δ

= T

• Finally, for any ϕ ∈ D,

〈T ∗δ

′

, ϕ〉 =

T (x) ,



′

( y), ϕ(x + y)





T (x) , −ϕ

′

(x)



= 〈T

′

, ϕ〉.

It follows that T ∗δ

′

= δ

′

∗ T = T

′

In addition, if T = R ∗ S , then T

′

= δ

′

∗ T = δ

′

∗ R ∗ S = R

′

∗ S .

Similarly, T

′

= T ∗δ

′

= R ∗ S

′

, wh ich proves the following theorem:

THEOREM 7.76 To compute the derivative of a convolution, it sufﬁces to take the

derivative one of the two factors and take the convolution with the other; in other

words, for any R, S ∈ D

′

, we have

[R ∗ S ]

′

= R

′

∗ S = R ∗ S

′

when R ∗ S exists. In the same manner, in three dimensions, for any S , T ∈ D

′

)

such that S ∗ T exists, we have

△(S ∗ T ) = △S ∗ T = S ∗△T .

7.6.g The Poisson equation

We have admitted t hat the electrostatic potential V created by a distribution

of charge ρ is g iven by

V ( r) =

4πǫ



ρ( r

′

− rk



4πǫ



ρ ∗

krk

