Appel W. Mathematics for Physics and Physicists
Подождите немного. Документ загружается.


Definitions and ex amples of distributions 187
x
1
x
1
a
−a
x
1
The δ distribution δ
a
−
1
2
δ
−a
+
1
2
δ The X distribution
7.2.c Support of a distribution
Two distributions S a nd T are e qual if 〈S , ϕ〉 = 〈T , ϕ〉 for any ϕ ∈ D. The y
are equal on an open subset Ω in RR
R
R
RR
n
if 〈S, ϕ〉= 〈T , ϕ〉 for any ϕ ∈ D such
that the support of ϕ is contained in Ω (i.e., for any ϕ ∈ D which is zero
outside Ω).
Example 7.17 Let H be th e Heaviside function. The regular distributions 1 and H are equal
on ]0,+∞[. Indeed, for any function ϕ ∈ D wh ich vanishes on R
−
, we have
〈1, ϕ〉 =
Z
+∞
−∞
1 ·ϕ(x) dx =
Z
+∞
0
ϕ(x) dx = 〈H ,ϕ〉.
Similarly, X and δ are equal on ]−
1
2
,
1
2
[.
Consider now all t he open subsets Ω on wh ich a given distribution T is
zero (i. e. , is equal to the zero distribut ion on Ω). The union of t hese open sets
is itself an open set . One can then show (but this is not obvious and we will
omit it here, see [80] for instance) that this is the largest open set on which T
is zero. Its complement, which is therefore closed, is called the support of the
distribution T , and is denoted supp(T ).
Example 7.18 The suppor t of the Dirac distribution centered at 0 is supp(δ) = {0}, and more
generally, for a ∈ R, we have supp(δ
a
) = {a}.
The support of t h e Dirac comb is supp(X) = Z.
7.2.d Other examples
PROPOSITION 7.19 Let ϕ ∈ D(R) be a test function. The quantity
Z
−η
−∞
ϕ(x)
x
dx +
Z
+∞
+η
ϕ(x)
x
dx
has a finite limit as [η → 0
+
]. M oreover, the ma p
ϕ 7−→ lim
η→0
+
Z
|x|>η
ϕ(x)
x
dx (7.2)
is linear and continuous on D(R).
Proof. Because of its l ength, the proof of this theorem is given in Appendix D,
page 600.

188 Distributions I
DEFINITION 7.20 The Cauchy principal value of 1/ x is the distr ibution on
R defi ned by its action on any ϕ g iven by
pv
1
x
, ϕ
·
= pv
Z
ϕ(x)
x
dx
def
= lim
η→0
+
Z
|x|>η
ϕ(x)
x
dx.
It s hould be emphasized that this integral is defined symmetrically around the
origin. It is this symmetry which provides the ex istence of the limit d efining
the distribution. The distribution pv 1/x can also be seen as the derivative
of the regular distrib ut ion associated to the locally integrable function x 7→
log |x| (see Exercise 8.4 on page 241).
Other properties and examples of physical applications of the Cauchy
principal value will be given in the next chapter. In addition, a generalization
of the method leading to the definition of a distribution from the function
x 7→ 1/x (which is not locally integrable) is given in Exercises 8.5 and 8.6 on
page 241.
7.3
Elementary properties. Oper ations
7.3.a Operations on distributions
We wish to define certain operations on distributions, such as translations,
scaling, derivation, and so on. For this purpose, the method will be consis-
tently the same:
Consider how those operations are defined for a locally integrable func-
tion; write them, in the la ngua ge of distributions, for the associated
regular distribution; then generalize this to an arbitrary distribution.
For instance, for any locally integrable function f on R
n
and any a ∈ R
n
,
we define the translate f
a
of the function f by
∀x ∈ R f
a
(x)
def
= f (x −a).
In other words, the graph (in R
n+1
) of the function f has been translated by
the vector a:
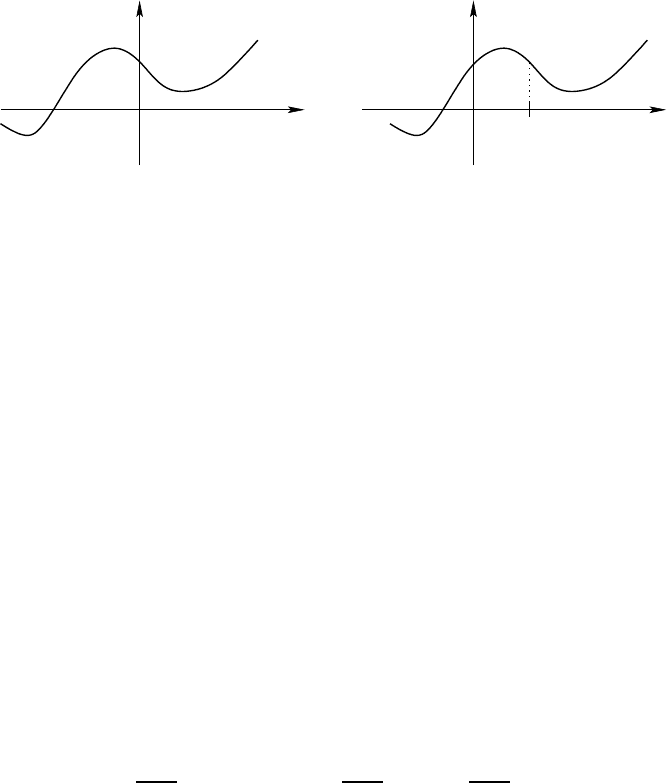
Elementary properties. Operations 189
f f
a
a
The regular distribution associated to this function, which is also denoted
f
a
, th erefore satisfies
〈f
a
, ϕ〉 =
Z
f (x − a) ϕ(x) dx =
Z
f ( y) ϕ( y + a) dy =
f , ϕ
−a
.
This can be generalized to an arbitrary distribution T in the following man-
ner:
DEFINITION 7.21 The translate of the distrib ut ion T by a, denoted T
a
or
T (x −a), is defined by
〈T
a
, ϕ〉
def
=
T , ϕ
−a
for any ϕ ∈ D(R
n
),
which is also written
T (x −a), ϕ(x)
def
=
T (x), ϕ(x + a)
.
The reader ca n easily check that the number
T , ϕ
−a
exists and that the map
ϕ 7→
T , ϕ
−a
is indeed linear and continuous.
Remark 7.22 As in Remark 7.15, the notation T (x − a) is simply synonymous with T
a
; simi-
larly, with an abuse of language, ϕ(x −a) sometimes designates (for physicists more than for
mathematicians) the function t 7→ ϕ(t −a) and not the value of ϕ at x −a.
Example 7.23 Let a ∈ R. The translate by a of the Cauchy principal value is
pv
1
x − a
: ϕ 7−→ lim
η→0
+
Z
a−η
−∞
ϕ(x)
x − a
dx +
Z
+∞
a+η
ϕ(x)
x − a
dx
.
By analogous reasoning, we define the “transpose” of a distribution. For
a function f : R
n
→ C, we denote by
ˇ
f t he transpose of f , which is the
function x 7→
ˇ
f (x)
def
= f (−x). If f is locally integrable, then so is
ˇ
f ; hence
both f and
ˇ
f define regular distributions. Moreover, for any ϕ ∈ D(R
n
), we
have
〈
ˇ
f , ϕ〉 =
Z
ˇ
f (x) ϕ(x) dx =
Z
f (−x) ϕ(x) dx
x=−t
=
Z
f (t) ϕ(−t) dt = 〈f , ˇϕ〉.
This justifies the following definition:
190 Distributions I
DEFINITION 7.24 (Transpose) Th e transpose of a distribution T on R
n
, de-
noted
ˇ
T or T (−x), is defined by
〈
ˇ
T , ϕ〉
def
= 〈T , ˇϕ〉,
which can also be written:
T (−x), ϕ(x)
def
=
T (x), ϕ(−x)
for any ϕ ∈ D(R
n
).
Similarly, for any a ∈ R
∗
, a change of scale defines the dilation by a of a
function f by x 7→ f (ax). The regular distribution a ssociated to the dilation
of a function satisfies
f (ax), ϕ(x)
=
Z
f (ax) ϕ(x) dx =
Z
f (x) ϕ
x
a
dx
|a|
=
1
|a|
D
f (x), ϕ
x
a
E
.
This leads to the following generalization:
DEFINITION 7.25 (Dilat ion) Let a ∈ R
∗
. The dilation of a distribution T by
the factor a, denoted T (ax), is defined by
T ( ax), ϕ(x)
def
=
1
|a|
D
T (x), ϕ
x
a
E
for any ϕ ∈ D(R).
Dilations of a distribution on R
n
are defined in exactly the same manner.
However, the jacobian associated to the change of variable y = ax is |a|
n
instead of |a|, which gives the dilation relations
T (a x), ϕ( x)
=
1
|a|
n
D
T ( x), ϕ
x
a
E
on R
n
.
There is , unfortunately, no general definition of the product of two dis-
tributions.
6
Already, if f a nd g are two locally integrable functions (hence
defining regular distributions), their product is not necessarily locally inte-
grable.
7
However, if ψ is a function of class C
∞
, then for any ϕ ∈ D, the
product ψϕ is a test function (still being C
∞
and with bounded support); if
f is locally integrable, then ψ f is also locally integ rab le. From the point of
view of distribut ions, we ca n write
〈ψ f , ϕ〉 =
Z
ψ(x) f (x)
ϕ(x) dx =
Z
f (x)
ψ(x) ϕ(x)
dx = 〈f , ψϕ〉.
6
In particular, i t is easy to notice that taking the square of the Dirac distribution raises
arduous questions. However, it turns out to be p o ssible to define a p roduct i n a larger space
than the space of distributions, the space of generalized distributions of Colombeau [22, 23].
7
Simply take f (x) = g(x) = 1/
p
x.

Elementary properties. Operations 191
This leads us to state the following definition:
DEFINITION 7.26 (Product of a distribution by a CC
C
C
CC
∞
function) Let T ∈ D
′
be a distr ibution and let ψ be a function of clas s C
∞
. The product ψT ∈ D
′
is defined by
〈ψT , ϕ〉
def
= 〈T , ψϕ〉 for any ϕ ∈ D.
By applying this definition to the Dirac distribution, the following funda-
mental result follows:
THEOREM 7.27 Let ψ be a function of C
∞
class. Then we have
ψ(x) δ(x) = ψ(0) δ(x) and in particular x δ(x) = 0.
Similarly, we have the relation
ψ(x) X(x) =
X
n∈Z
ψ(n) δ(x −n).
Proof. If ψ is o f C
∞
class, then by definition
〈ψδ, ϕ〉 = 〈δ, ψϕ〉 = ψ(0 ) ϕ( 0 ) = ψ(0) 〈δ, ϕ〉 =
ψ(0) δ, ϕ
.
Since any test function has bounded support, the last formula follows by simple lin-
earity.
It is important to notice that, for instance, the product H δ makes no
sense here!
THEOREM 7.28 The equation x T (x) = 0, with unknown a distribution T , admits
the multiples of the Dirac distribution as solutions, and they are the only solutions:
x T (x) = 0 ⇐⇒
T = αδ, with α ∈ C
.
Remark 7.29 If ψ is merely continuous, the product ψT cannot be defined for an arbitrary
distribution T , but the product ψδ can in fact still be defined. Similarly, if ψ is of C
1
class
(in a neighborhood of 0), the product ψδ
′
can be defined (see the next section).
7.3.b De rivative of a distribution
The next goal is to define derivation in the space of distributions. As before,
consider a locally integrable function f ∈ L
1
loc
, and assume moreover that it
is differentiable and its derivative is also locally integrable. Then the regular
distribution associated to f
′
is given by
f
′
, ϕ
=
Z
f
′
(x) ϕ(x) dx = −
Z
f (x) ϕ
′
(x) dx = −
f , ϕ
′
.
The passage to the second integral is done by integrating by par ts; th e bound-
ary terms vanish because ϕ has bounded support (this is one reason for th e
“very restrictive” choice of the space of test functions). This justifies the
following generalization:
192 Distributions I
DEFINITION 7.30 The derivative of a distribution T ∈ DD
D
D
DD(RR
R
R
RR)
′
is defined by
T
′
, ϕ
def
= −
T , ϕ
′
for any ϕ ∈ D(R). (7.3)
Similarly, the higher order derivatives are defined by induction by
¬
T
(m)
, ϕ
¶
def
= (−1)
m
¬
T , ϕ
(m)
¶
for any ϕ ∈ D and a ny m ∈ N.
Example 7.31 The function x 7→ log |x| is locally integrable and therefore defines a regular
distribution. However, its derivative (in th e usual sense of functions) x 7→ 1/x is not locally
integrable; therefore it does not define a (regular) distribution.
However, if the derivation is performed directly in the sense of distributions,
log |x|
′
is a
distribution (it is shown in Exercise 8.4 on page 241 that it is the Cauchy principal value pv
1
x
).
If working on R
n
, a similar computation justifies the definition of partial
derivatives of a distribution T ∈ D
′
(R
n
) by
∂ T
∂ x
i
, ϕ
def
= −
T ,
∂ϕ
∂ x
i
for ϕ ∈ D(R
n
) and 1 ¶ i ¶ n. Partial derivatives of higher order are obtained
by successive applications of these rules: for instance,
∂
3
T
∂ x
2
1
∂ x
2
, ϕ
= (−1)
3
T ,
∂
3
ϕ
∂ x
2
1
∂ x
2
.
In particular, on R
3
, we have
∂ T
∂ x
, ϕ
= −
T ,
∂ϕ
∂ x
,
∂ T
∂ y
, ϕ
= −
T ,
∂ϕ
∂ y
,
∂ T
∂ z
, ϕ
= −
T ,
∂ϕ
∂ z
.
Similarly, the laplacian being a differential operator of order 2, we define:
DEFINITION 7.32 The laplacian of a distribution on R
n
is given by
〈△T , ϕ〉
def
= 〈T , △ϕ〉 for any ϕ ∈ D(R
n
).
THEOREM 7.33 (Differentiability of distributions) Any distribution on R
n
ad-
mits partial derivatives of arbitrar y order. Any partial derivative of a distribution is
a distribution.
COROLLARY 7.33 .1 Any locally integrable function on R defining a distribution,
it is infinitely differentiable in the sense of distributions:
∀f ∈ L
1
loc
(R) ∀k ∈ N f
(k)
∈ D
′
(R).

Dirac and its derivatives 193
At the age of sixteen, Oliver Heaviside (1850—1925), born in a
very poor family, had to leave school. At eighteen, he was hired
by Charles Wheatstone, the inventor of the telegraph. He then
studied t h e differential equations which govern electri c signals
and in particular the “square root of the derivative” (he wrote
p
d/dt H (t) = 1/
p
πt), wh ich gave apoplexies to the mathe-
maticians of Cambridge.
9
One of his papers occasioned the se-
vere disapproval of the Royal Society. He defended vector analysis
(Maxwell was in favor of the use of quaternions instead of vec-
tors), symbolic calculus, and the use of divergent series, and had
faith in methods “whic h work” before being rigorously justified.
When Laurent Schwartz presented the theory of d istributions, this result
seemed particularly marvelous to the audience: all distributions are infinitely
differentiable and their successive derivatives are themselves distributions.
8
Thus, if we consider a locally integrable function, however irregular, its as-
sociated distribution is still infinitely differentiable. This is one of the key
advantages of the theory of distributions.
7.4
Dirac and its derivatives
7.4.a The Heaviside distribution
A particularly important e xample is the Heaviside distribution, which we will
use constant ly.
DEFINITION 7.34 The Heaviside function is the function H : R → R de-
fined by
H (x) =
0 if x < 0,
1/2 if x = 0,
1 if x > 0.
8
Mathematicians had been aware for less than a centur y of the fact that a continuous func-
tion could be very far from differentiable (since there exist, for instance, functions continuous
on all of R which are nowhere differentiable, as shown by Peano, Weierstrass, and others).
9
Enamored of rigor from a recent date only and, therefore, as inflexible as any new convert.
The reader interested in the “battle” between Oliver Heaviside and the rigorists of Cambridge
can read with profit the article [4 8 ].

194 Distributions I
DEFINITION 7.35 The Heaviside distribution is the regular distr ibution as-
sociated to the Heaviside function. It is thus defined by
∀ϕ ∈ D(R) 〈H , ϕ〉
def
=
Z
+∞
0
ϕ(x) dx.
The derivative, in the sense of distributions, of H is then by defi nit ion
H
′
, ϕ
= −
H , ϕ
′
= −
Z
+∞
0
ϕ
′
(x) dx = −
ϕ
+∞
0
= ϕ(0),
from which we deduce
THEOREM 7.36 The derivative of the Heaviside distribution is the Dirac distribution
H
′
= δ in the sense of distributions.
7.4.b Multidimensional Dirac distrib utions
In many cases, the physicist is working in R
3
or R
4
. We will define here
the notions of point-like, linear, and surface Dirac distribut ions, which occur
frequently in electromagnetism, for instance.
Point-like Dirac distribution
Recall that in three dimensions the Dirac distribution is defined by
δ
(3)
, ϕ
def
= ϕ(0).
The common notation δ
(3)
( r) = δ(x) δ( y) δ(z) will be explained in Sec-
tion 7.6.b. Most authors use δ instead of δ
(3)
since, in general, there is no
possible confusion. Thus a point-like charge in electrostatics is represented by
a distr ibution ρ( r) = q δ( r − a). Note that, when it acts on a space variable,
the three-dimensional Dirac distrib ut ion has the dimension of the inverse of a
volume:
[δ] =
1
[L]
3
,
which implies that ρ( r) has the dimension Q/L
3
of a volum density of
charge.
Surface Dirac distribution
To describe a surface carrying a uniform charge, we use the surface Dirac
distribution:
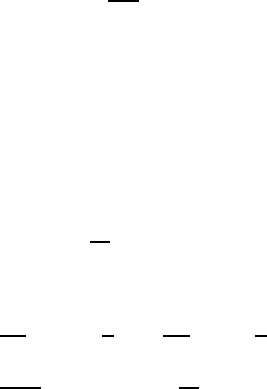
Dirac and its derivatives 195
DEFINITION 7.37 Let S be a smooth surface in R
3
. The (normalized) Dirac
surface distribution on S is given by its action on any test function ϕ ∈
D(R
3
):
〈δ
S
, ϕ〉
def
=
ZZ
S
ϕ d
2
s,
where d
2
s is the integration element over the surface S . In electromagnetism,
a uniform surface density σ
0
on S is described by the distribution σ
0
δ
S
.
This can be extended to nonuniform surface distribution, since we know how
to multiply a distribution by a function of C
∞
class. So a distribution of
charge σ( r) of C
∞
class on a surface S is represented by σ( r) δ
S
.
Example 7.38 In R
3
, for R > 0, we denote by δ
kxk−R
the Di rac surface distribution δ
S
,
where S is the sphere S =
x ∈ R
3
; kxk = R
.
It should be noted that when working with spacial variables in R
3
, th e
surface Dirac distribution has the dimension of the inverse of length:
[δ
S
] =
1
[L]
,
which can be recovered by writing (in a heuristic manner, indicated by large
quotes)
〈δ
S
, ϕ〉 =
“
ZZZ
δ
S
( r) ϕ( r) d
3
r
”
=
ZZ
S
ϕ( r) d
2
s.
Exercise 7.1 Let S be a surface in R
3
and let a ∈ R. Denote by S
′
the surface obtained
from S by homothety with coefficient 1/a. Show that
δ
S
(a r) =
1
|a|
δ
S
′
( r).
◊ Solution: Let ϕ ∈ D(R
3
). Then we have
δ
S
(a r), ϕ
def
=
1
|a|
3
D
δ
S
, ϕ
r
a
E
=
1
|a|
3
ZZ
S
ϕ
r
a
d
2
r (definition)
=
1
|a|
3−2
ZZ
S
′
ϕ( x) d
2
x =
1
|a|
〈δ
S
′
, ϕ〉.
Curvilinear Dirac distribution
By the same method, a density of charge on a curve is defined using the
curvilinear Dirac distribution:
DEFINITION 7.39 Let L be a curve in R
3
. The unit curvilinear Dirac
distribution on L is defined by its action on any test function ϕ ∈ D(R
3
)
given by
〈δ
L
, ϕ〉
def
=
Z
L
ϕ d ℓ,

196 Distributions I
x
y
+δ/k
−δ/k
k/2
−k/2
Fig. 7.1 — The distribution δ
′
can be seen as two Dirac peaks with opp osite signs infinitely
close to each other — that is, a dipol e.
where dℓ is the integration element over L . In electromagnetism, a density
of charge c( r) supported on the curve L is represented by the distribu-
tion c( r) δ
S
.
When working with spacial variables in R
3
, the curvilinear Dirac distribu-
tion has the dimension of the inverse of a surface:
[δ
L
] =
1
[L]
2
.
7.4.c The dis tribution δ
′
As seen in the defining formula (7.3), the derivative δ
′
of the Dirac distribu-
tion is defined by
δ
′
, ϕ
def
= −ϕ
′
(0) for any test function ϕ ∈ D.
Note that if ϕ is a test function, then
δ
′
, ϕ
= −ϕ
′
(0) = −lim
k→0
ϕ
k
2
−ϕ
−
k
2
k
= −lim
k→0
1
k
δ
x −
k
2
−δ
x +
k
2
, ϕ
,
from which we conclude that (note the signs!)
δ
′
(x) = lim
k→0
1
k
δ
x +
k
2
−δ
x −
k
2
.
This formula is interpreted as follows. The distribution represents a positive
charge 1/k and a negative charge −1/k, situated at a distance equal to k, in
the limit wh ere [k → 0] (see Figure 7.1). Hence the distribution δ
′
represents
a dipole, aligned on the horizont al axis (O x) with dipole moment −1, hence
oriented toward negative values of x.
