Appel W. Mathematics for Physics and Physicists
Подождите немного. Документ загружается.

Conformal maps 157
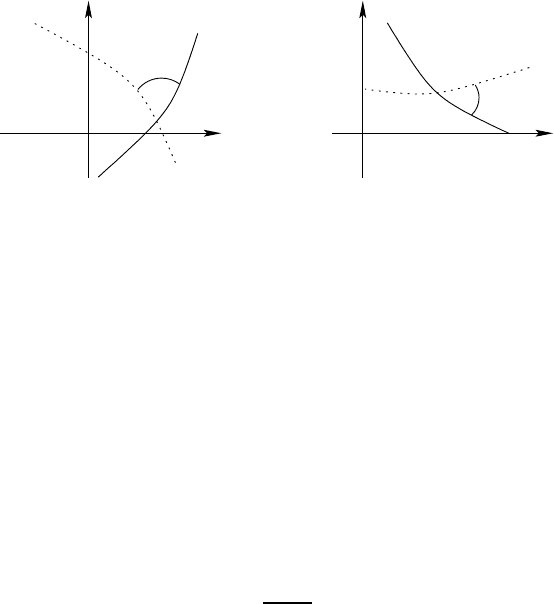
γ
2
θ
γ
1
γ
′
1
θ
γ
′
2
Conversely, if f is a map w h ich is R
2
-differentiable and preserves angles, the n at
any point d f is an endomorphism of R
2
which preserves angles. Since f also preserves
orientation, its determinant is positi ve, so d f is a similitude, and its matrix is exactly
as in equation (6.1). The Cauchy-Riemann equations are immediate consequences.
Remark 6.5 An antiholomorphic map also preserves angles, but it reverses the orientati on.
6.1.b The Rie mann mapping theorem
DEFINITION 6.6 Two open subsets U and V of C are homeomorphic if
there exists a bijection f : U → V such that f and its inverse f
−1
are both
continuous. Such a map is called a homeomorphism of U into V .
Remark 6.7 In fact, in this case the continuity of f
−1
is an unnecessary condition, because it
turns out to be implied by the continuity of f , the fact that f is bijective, and that U and V
are open. However, this is quite a delicate result.
Example 6.8 The complex plane C is homeomorphic to the (interior of the) unit disc, through
the homeomorphism
f : z 7−→
z
1 + |z|
.
See also Exercise 6.2 on page 174.
DEFINITION 6.9 Two open sets U and V are conformally equivalent if there
exists an injective conformal application f : U → C such th at V = f (U ).
THEOREM 6.10 (Riemann mapping theorem) Let U be any open subset of C
such that U 6= C. If U is homeomorphic to the unit disc D = B(0 ; 1), then U is
conformally equivalent to D.
In general, two open sets which are homeomorphic are not conformally
equivalent. For instance, two annuli r
1
< |z| < r
2
and r
′
1
< |z| < r
′
2
are
conformally equivalent if and only if r
′
2
/r
′
1
= r
2
/r
1
.
So the Riemann mapping theorem is a very strong result, since any c on-
nected and simply connected open set, except C, can be transformed, via a confor-
mal map, into the unit disc.
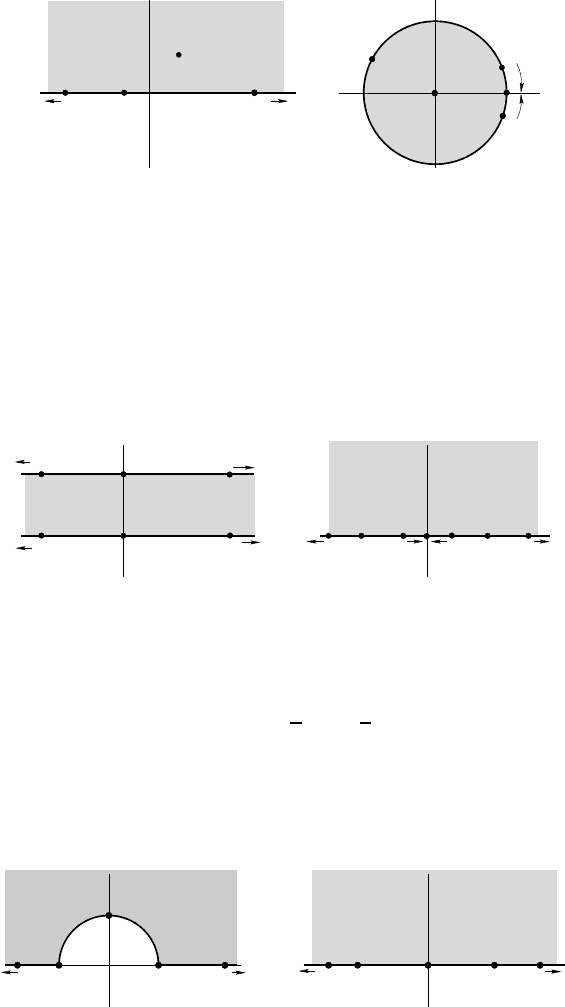
To illustrate, consider in Figure 6.1 on the next page some open subset
U of the complex plane. Riemann’s theorem guarantees the existence of a
conformal map w = f (z) such that B(0 ; 1) = f (U ). The boundary ∂ U
of U is mapped to the unit disc C (0 ; 1). (This seems natural, but to make

158 Conformal maps
U
P
Q
z w = f (z)
D
0
Q
′
Fig. 6.1 — The open subset U being homeomorphic to the unit disc, it is conformally
equivalent to it. There e xists therefore a conformal map w = f (z) such that the
image of U by f is D. One can ask that f (P ) = 0 and f ( Q) = Q
′
.
sense of it we need to know in general that f extends to the boundary of U .
That this is th e case is shown by Carathéodory and Osgood, provided this
boundary is a simple closed continuous curve; in the explicit examples b elow,
this e xtension will be obvious.) Moreover, it is possible to impose additional
conditions on f , for instance, by asking that a particular point P ∈ U be
mapped to the center of the unit disc: f (P ) = 0, and by asking also t hat a
point Q ∈ ∂ U be mapped to a given point on the unit circle.
It is important to note that, while Riemann’s theorem tells us that the
conformal representa tion of U exists theoretically, it does not tell how to find
it. Physicists like Joukovski
1
found clever conformal representations of various
domains in the plane; these are useful to compute easily (in terms of computer
time) the effects of a fluid flowing around those domains.
6.1.c Examples of conformal maps
The following examples of conformal maps are given without proof. The
reader is invited to check their propert ies by herself.
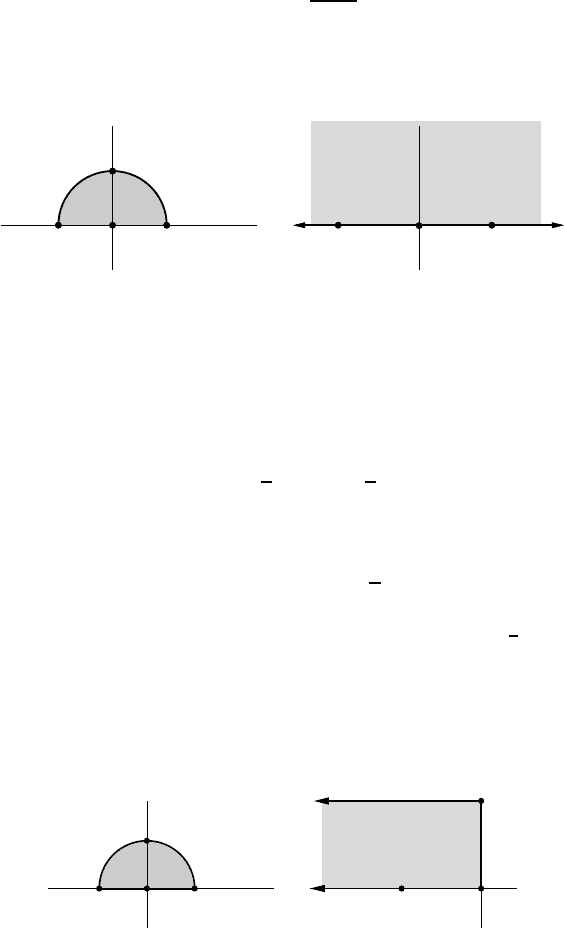
Representation of a half-plane into a disc
Let z
0
be any point in the open upper half-plane. Let
w = f (z) =
z − z
0
z −¯z
0
.
The upper half-plane is then transformed bijectively into the interior B(0 ; 1)
of the unit circle. The point z
0
is mapped to 0. The real points x tending
to either +∞ or −∞ are s ent to th e same limit 1. As z runs over the real
1
Nicolaï Joukovski (1847—1921), a Russian physicist, studied hydrodynamics and aerody-
namics. He discovered a conformal map z 7−→
1
2
(z + a
2
/z), which transforms th e circles going
through a and −a into a profile si milar to an air plane wing.
Conformal maps 159
axis in increasing order, w goes around the unit circle in the counterclockwise
direction, starting and ending at the point w = 1.
BA
P (z
0
)
C
z w = f (z)
B
′
P
′
(0)
A
′
C
′
Infinite strip of widt h a
Using the complex exponential function, we can transform an infinite strip
of width a into the upper half-plane, by putting
w = f (z) = e
πz/a
.
The points on th e real axis and the line Im(z) = a in the limit Re(z) → −∞
both converge to 0, while in the limit Re(z) → +∞, the real points converge
to +∞ and those with height a converge to −∞ (on the real axis).
A B C
D E F
z
w = f (z)
A
′
B
′
C
′
D
′
E
′
F
′
−1 0 1
Half-plane outside a half-circle
The upper half- plane minus a half-circle is mapped to t he upper half-plane by
putting
w = f (z) =
a
2
z +
1
z
,
where a is an arbitrary real number. This transformation is not conformal at
the points −1 and 1 (the derivative vanishes), which explains that the right
angles between the half-circle and the real axis are transformed into “flat”
angles (equal to π).
A B
C
D E
z w = f (z)
A
′
B
′
C
′
D
′
E
′
−a 0 a
160 Conformal maps
Half-circle
The unit upper half-circle is mapped into the upper half-plane by putting
w = f (z) =
1 + z
1 − z
2
.
The point −1 (C in the fi gure) is mapped to 0 while the point 1 (A) is mapped
to infinity on the real axis (either +∞ or −∞, depending on whether one
approaches A on the real axis or on the b oundary of t he half-circle).
C
B
AD
z w = f (z)
A
′
B
′
C
′
D
′
A
′
−1 0 1
Some conformal mappings into the unit disc
The exterior of the unit disc is mapped conformally to the interior by simply
putting w = 1/z.
Also the exterior of an ellipse wit h major axis equal to 2 cosh(α) and minor
axis equal to 2 sinh(α) is mapped to the interior of the unit disc by putting
w = f (z) =
1
2
z e
−α
+
1
z
e
α
.
Other examples
The angular sector {r e
iθ
; 0 < r < 1, 0 < θ <
π
2
} (a quarter-disc) is mapped
into the upper half-d isc by putting w = z
2
.
Similarly, the angular sector of angle π/k (with k ∈ R, k ¾
1
2
) is mapped
into the upper half-plane by putting w = z
k
.
The upper half-disc in mapped to a semi-infinite strip (infinite to the left)
by putting w = log z with the logarithm defined by a cut in the lower h alf-
plane.
C
B
AD
z w = f (z)
D
′
B
′
A
′
C
′
D
′
−1 0
The same transformation maps the upper half-plane into an infinite strip.

Conformal maps 161
The German mathematician Hermann Schwarz (1843—1921) suc-
ceeded his teacher Weierstrass at the University of Berlin in 1892.
He worked on conformal mappings, potential theory (proving
the existence of a solution to the Dirichlet problem i n 1870), and
partial differential equations.
6.1.d The Schwarz-Christoffel transformation
We are now looking for a conformal transformation that will map a domain
bounded by a polygonal line into a simpler domain, for instance, the upper
half-plane (or the unit disc, but we already know how to go from th e unit disc
to the upper half-plane). For this, we use t he following result:
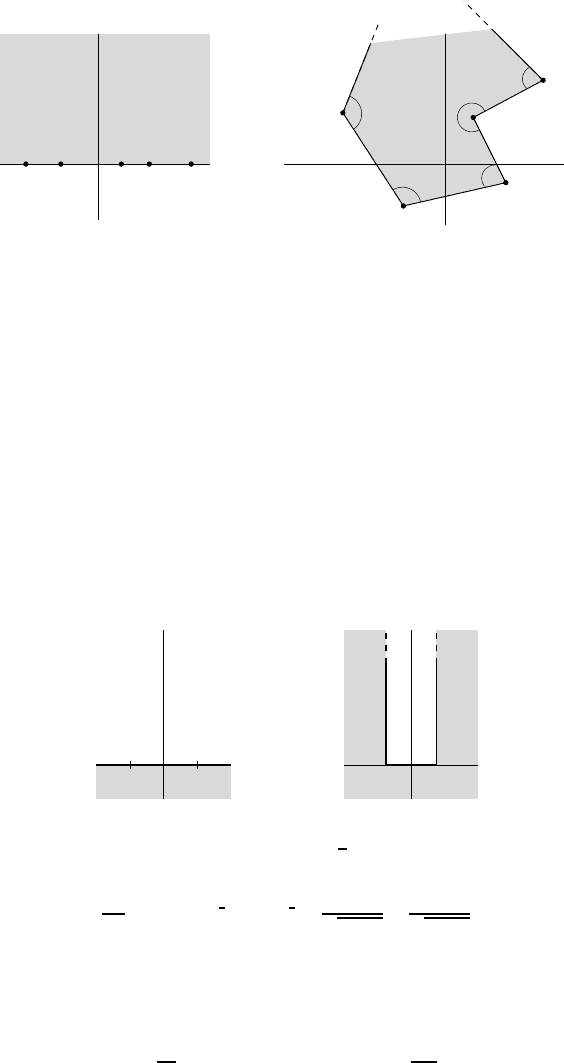
THEOREM 6.11 (Schwarz-Christoffel transformation) Let n ∈ N be an integer,
x
1
, . . . , x
n
real numbers, and α
1
, . . . , α
n
real numbers between 0 and 2π. Let fina lly
a ∈ C be an arbitrary complex number. The map given by
dw
dz
= a(z − x
1
)
α
1
/π−1
(z − x
2
)
α
2
/π−1
···(z − x
n
)
α
n
/π−1
(6.2)
transforms the real axis into a polygonal curve with successive angles (α
1
, . . . , α
n
) and
transforms the upper half-plane into the domain bounded by this curve (see Figure 6.2
on the following page).
Formula (6.2) provides only a local expression of the map. By integrating
along a complex path, we obtain the equivalent formula
w = f (z) = a
Z
γ(z)
n
Y
i=1
(z
′
− x
i
)
α
i
π
−1
dz
′
+ w
0
,
where w
0
∈ C is an arbitrary constant and γ(z) is a path coming from infinity,
contained in the open upper half-plane a nd ending at z. Since the upper half-
plane is simply connected and the only poles of the function to integrate are
on the real axis, the result does not depend on the actual path we choose.
Remark 6.12
➀ Changing w
0
amounts simply to translating the image of the map.
➁ Changing the value of the constant a gives the possibility to make rotations (by chang-
ing the argument of a) or homoth eties (by changing its module).
➂ By imposing the condition
X
i
α
i
π
−1
= −2,
162 Conformal maps
A B C D E
x
1
x
2
x
3
x
4
x
5
z
w = f (z)
A
′
B
′
C
′
D
′
E
′
α
1
α
2
α
3
α
4
α
5
Fig. 6.2 — The Schwarz-Christoffel transform maps the open upper half-plane into t h e
domain Ω bounded by the polygonal curve with successive angles α
1
, . . . , α
n
.
the polygonal line is cl o sed and we obtain a closed polygon. A n infinite polygon (when
the condition does not hold) i s a limiting case of closed polygons.
➃ If the problem to solve is to find a conformal mapping transforming the upper half-
plane into a polygonal domain (either closed or open), it is possible to choose arbitrarily
three of the real numbers (x
1
, . . . , x
n
). The others are then imposed by the various
quantities in t h e picture.
➄ It i s often convenient to move one of the x
i
(for instance, x
1
or x
n
) to infinity, which
simplifies t h e computations.
Example 6.13 We describe how to use the Schwarz-Christoffel transform to map conformally
an infinite h al f-strip into the upper half-plane.
−1 1
z
−−−−−−→
w = f (z)
−b b
w
The two angles in the polygonal line are equal to
π
2
and we fix the choice of x
1
= −1 and
x
2
= 1. So we need to solve
dw
dz
= a(z + 1)
−
1
2
(z −1)
−
1
2
=
a
p
z
2
−1
=
α
p
1 − z
2
,
where a is a constant to be determined and α = −ia. We therefore put
w = f (z) = α arcsin(z) + B,
and to have f (1) = b and f (−1) = −b, we must take B = 0 and α = 2b/π. Hence the
solution is
w =
2 b
π
arcsin(z), i.e., z = sin
πw
2 b
.

Applications to potential theory 163
Elwin Christoffel (1829—1900), born in Montjoie Aachen (pre-
sent-day Monshau) in Germany, from a family of clothes mer-
chants, studied in Berlin from 1850, where he had in particular
Dirichlet as a teacher (see page 171). He defended hi s doctoral on
the flow of electricity in homogeneous bodies, t h en taught there
before ending h is career in the new University of Strasbourg.
Shy, irritable, asocial, Christoffel was nevertheless a brilliant
mathematician who studied Riemannian geometry, introducing
the Christoffel symbols, as well as conformal mappings.
6.2
Applications to potential theory
(This section may be omitted for a first reading; it is preferable to study it w ith some
knowledge of Green fu nctions, which we will present later.)
Conformal transformations are usef ul to solve a number of problems of
the type “Poisson equation with boundary condition,” for instance, the prob-
lem of the diffusion of h eat in a solid, in a stationary regime, with the
temperature fixed on th e boundary of the solid; or the problem of the elec-
trostatic field created by a charge distribution in the presence of conductors.
The main idea is to transform the “boundary” of th e problem, w hich may
be complicated, into a simpler boundary, by a conformal map. In particular,
the Dirichlet problem for a half-plane or for a circle (see page 170) can b e
solved, and t his makes it possible to solve it, at least in principle, for more
complicated boundaries.
THEOREM 6.14 Let Ω ⊂ R
2
and Ω
′
⊂ R
2
be two domains of R
2
≃ C and f a
bijective conformal map from Ω into Ω
′
. Let ϕ : Ω → R be a real-valued function,
with laplacian denoted by △
(x, y)
ϕ =
∂
2
ϕ
∂ x
2
+
∂
2
ϕ
∂ y
2
. Moreover, denote (u, v)
def
= f (x, y)
and consider the image of by the change of variable f :
Φ(u, v)
def
= ϕ
f
−1
(u, v)
(in other words, Φ = ϕ ◦ f
−1
). Then, if we denote △
(u,v)
Φ
def
=
∂
2
Φ
∂ u
2
+
∂
2
Φ
∂ v
2
the
laplacian of Φ in the new coordinates, we have
△
(x, y)
ϕ =
f
′
(z)
2
△
(u,v)
Φ.
Proof. This is an elementary but tiresome computation. It suffices to use the chain
164 Conformal maps
rule formulas
∂
∂ u
=
∂ x
∂ u
∂
∂ x
+
∂ y
∂ u
∂
∂ y
and
∂
∂ v
=
∂ x
∂ v
∂
∂ x
+
∂ y
∂ v
∂
∂ y
for partial derivatives, together with the Cauchy-Riemann relations.
COROLLARY 6.15 The property that a function is harmonic is invariant by confor-
mal transformation.
Hence, suppose we have to solve a problem like the Dirichlet problem,
namely, we must find a harmonic function ϕ on a domain domain Ω ∈ R
2
such that ϕ(z)
∂Ω
= f (z), where f : ∂ Ω → C is a given function. If we know
how to transform Ω by conformal mapping into a half-circle or a half-plane,
we can solve the associated Dirichlet problem and then perform the inverse
change of variable, which will preserve the harmonicity of the solution.
However, in general the goal is to solve not a La place equation △ϕ = 0,
but rather a Poisson equation
△ϕ(x, y) = δ(x − x
0
, y − y
0
).
It is therefore necessary to first determine how this equation is transformed
by a conformal mapping. In a dilation (change of scale) x 7−→ ax in the
argument of a Dirac distribution (see Chapter 7), a factor 1/ |a|
d
appears,
where d is the dimension. Here, we deal with two dimensions and, locally,
a conformal transformation is simply a similitude, with homothety factor
given by |f
′
(z)|. We have th erefore the following result (see T heorem 7.45 on
page 199 for a generalization when f is not bijective):
THEOREM 6.16 Let Ω ⊂ R
2
and Ω
′
⊂ R
2
be two domains of R
2
≃ C and let f
be a bijective conformal mapping of Ω into Ω
′
. Then for (x
0
, y
0
) ∈ Ω, we have
δ
f (x, y) − f (x
0
, y
0
)
=
1
f
′
(x
0
, y
0
)
2
δ(x − x
0
, y − y
0
).
As a consequence, we have th e following result:
THEOREM 6.17 Let Ω ⊂ R
2
and Ω
′
⊂ R
2
be two domains of R
2
≃ C and let f
be a bijective conformal mapping of Ω into Ω
′
. L et ϕ : Ω → R be a real-valued
function and let Φ be the image of ϕ by the change of variable f . Then, if ϕ satisfies
the Poisson equation
△
(x, y)
ϕ = δ(x − x
0
, y − y
0
),
its image by the conformal map f also satisfies the Poisson equation in the new
coordinates:
△
(u,v)
Φ = δ
f (x, y) − f (x
0
, y
0
)
.

Applications to potential theory 165
6.2.a Application to electrostatics
We will give an example of a pplication of those theorems to solve the Dirichlet
problem in the situation corresponding to electrostatics. We consider, in a two-
dimensional space, a conductor which leaves a “hole” sha ped like an infinite
half-strip, denoted Ω (see Figure 6.3).
Now, we would like to compute the potential created by an arbitrary distri-
bution of charge ρ(x, y). For this, because of t he linearity of the electrostatic
Poisson equation (△ϕ = −ρ/ǫ
0
), we will see (Chapter 7) that it suffices to find
the potential G(x, y ; x
0
, y
0
) created at the point (x, y) by a Dirac distribution
at (x
0
, y
0
), which satisfies
(C )
(
△G(x, y ; x
0
, y
0
) = δ(x − x
0
, y − y
0
) where △ =
∂
2
∂ x
2
+
∂
2
∂ y
2
,
G(x, y ; x
0
, y
0
) = 0 for any (x, y) ∈ ∂Ω and (x
0
, y
0
) ∈ Ω.
Once this f unction is found, the solution to the problem is given by
2
ϕ(x, y) = −
1
ǫ
0
ZZ
Ω
ρ(x
′
, y
′
) G(x, y ; x
′
, y
′
) dx
′
dy
′
.
One sh ould note that th e function G(x, y ; x
′
, y
′
) is not invariant under trans-
lations and therefore it does not depend only on x − x
′
and y − y
′
, because
of the presence of the conductor. T his function is called the Green function
for the problem.
To find this function G(x, y ; x
′
, y
′
), we start by introducing complex vari-
ables z = x + i y and w = u + iv; then we perform the conformal transfor-
mation w = sin(πz/2b) which, as we have seen, transforms Ω into t he upper
half-plane (see Figure 6.3). Then we look for the Green function of the new
problem, G (w ; w
′
), which satisfies, according to Theorem 6.17,
(C
′
)
¨
△
(u,v)
G (u, v ; u
′
, v
′
) = δ(u − u
′
, v − v
′
),
G (u, v ; u
′
, v
′
) = 0 ∀(u, v) ∈ f (∂ Ω), ∀(u
′
, v
′
) ∈ f (Ω),
where the image of the boundary ∂Ω is the real axis f (∂Ω) = R. In other
words, we are looking for the electrostatic response of a simpler system (a
half-plane) in t he presence of a n electric charge.
To solve this last problem, one can use the method of virtual images (wh ich
is justified, for instance, by means of the Fourier or Laplace transform): the
potential created by a charge at w
′
in the neighborhood of a conductor in
the lower ha lf-plane is the sum of the “free” potentials
3
created, first, by the
particle at w
′
and, second, by another particle, with the opposite charge,
placed symmetrically of the first with respect to the real axis (namely, at w
′
).
2
The physicist’s “proof” being that the quantity −ǫ
−1
0
ρ(x
′
, y
′
) G(x, y ; x
′
, y
′
) dx
′
dy
′
is the
potential c reated at (x, y) by the elementary charge ρ(x
′
, y
′
) dx
′
dy
′
.
3
I.e., of the Green functions tending to 0 at infinity.

166 Conformal maps
−b b
z
(a)
−−−−−−→
w = f (z)
−1 1
w
(b)
Fig. 6.3 — (a) The domain Ω left free by the conductor i s the set of points z = x + i y
with y > 0 and −b < x < b. The Dirichlet conditi o ns are that the potential
is constant, for instance, zero, on ∂Ω. (b) The image f (Ω) of the domain Ω is
the upper half-plane.
However, we will see in the cha pter concerning distributions that the Coulomb
potential
4
in two dimensions is simply
Φ(w) = −
q
2πǫ
0
log
w − w
′
.
G is thus equal to
G (w ; w
′
) =
q
2π
log
w −w
′
w −w
′
.
The Green f unction of the initial problem is obtained by putting, in the last
formula, w = sin(πz/2b), which gives
G(z ; z
0
) =
q
2π
log
sin
πz
2b
−sin
πz
0
2b
sin
πz
2b
−sin
πz
0
2b
,
or, by expanding in real form sin(a + ib) = sin a cosh b + i cos a sinh b,
G(x, y ; x
0
, y
0
) =
q
4π
×log
sin
πx
2 b
cosh
π y
2 b
−sin
πx
0
2 b
cosh
π y
0
2 b
2
+
cos
πx
2 b
sinh
π y
2 b
−cos
πx
0
2 b
sinh
π y
0
2 b
2
sin
πx
2 b
cosh
π y
2 b
−sin
πx
0
2 b
cosh
π y
0
2 b
2
+
cos
πx
2 b
sinh
π y
2 b
+ cos
πx
0
2 b
sinh
π y
0
2 b
2
.
Which, as the reader will notice, is not properly speaking something very
intuitive. However, it is remarkable how this computation has been done so
easily and without difficulty. This is the strength of conformal mappings.
4
The Coulomb potential in any dimension is a potential satisf ying the Laplace equation
△ϕ = −δ/ǫ
0
; Theorem 7.54 on page 208 shows that the th ree-dimensional Coulomb potential
is given by r 7→ 1/4πǫ
0
r, whereas in two dimensions Theorem 7.55 on page 208 shows that it
is r 7→ −(log r)/2πǫ
0
.
