Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Complex logarithm; multivalued functions 137

THEOREM 5.4 Let ℓ and ℓ

′

be two complex logarithms, deﬁned on C \ C and

C \C

′

, respectively. Then, for any z ∈ C \{C ∪C

′

}, the difference ℓ(z) −ℓ

′

(z) is

an integral multiple of 2πi.

This difference is constant on each connected component of C \{C ∪C

′

In addition, the principal logarithm sat isﬁes th e following property:

PROPOSITION 5.5 If z ∈ C is written z = ρ e

iθ

, with θ ∈ ]−π, π[ and

ρ ∈ R

+∗

, then L(z) = log ρ + iθ.

Example 5.6 Let ℓ(z) be the complex logarithm deﬁned by the cut R

. The reader will easily

check that, if z = ρ e

iθ

with θ ∈]0, 2π[ this time and ρ ∈ R

+∗

, then ℓ(z) = log ρ + iθ.

5.1.b The square root function

The logarithm is not the only f unction that poses problems when one tries to

extend it from the (half) real line to the complex plane. The “square root”

function is another.

Indeed, if z = ρ e

iθ

, one may be tempted to deﬁne the square root of z by

def

ρ e

iθ/2

. But a problem arises: the argument θ is only deﬁned up to

2π, and s o θ/2 is only d eﬁned up to a multiple of π; t hus, there is ambiguity

on the sign of

It is therefore necessary to specify which determination of the a rgument

will be used to d eﬁne the square root function. To this end, we introduce

again a cut and choose a continuous determination of the argument (which

always exists on a simply connected open set).

In the following, each time the complex square root function is mentioned,

it will be necessary to indicate, ﬁrst which is the cut, and second, which is the

determination of the argument considered.

Example 5.7 If the principal determination of the argument θ = Arg z ∈ ]−π, π[ is chosen,

one can deﬁned z 7−→

def

ρ e

iθ/2

and the restriction of “this” square root function to the

real axis is the usual real square root.

By chosing iR

−

as the cut, one can deﬁne a square root function on the whole real axis.

5.1.c Multivalued functions, Riemann surfaces

There is a trick to avoid having to introduce a cut for functions like the loga-

rithm or the square root. Physicists call these in general multivalued functions,

and mathematicians speak of functions deﬁned on a Riemann surface.

We sta rt with this second point of view.

The main idea is to replace the punctured complex plane (i.e., wit hout

0), on which the deﬁnition of a holomorphic logarithm or s quare root was

The notation “

” to designate the square root (this symbol is a deformation of the

letter “r”) was introduced by the German mathematician Christoff Rudolff (1500—1545).

138 Complex Analysis II

Georg Friedrich Bernhard Riemann (1826—1866), German math-

ematician of genius, brought extraordinary results in almost all

ﬁelds: differential geometry (riemannian manifolds, riemannian

geometry), complex analysis (Riemann surfaces, Riemann’s map-

ping theorem, the Riemann zeta function in relation to number

theory, th e nontrivial zeros of which are famously conjectured

to l ie on the line of real part

), integration (Riemann integral),

Fourier analysis (Riemann-Lebesgue theorem), differential calcu-

lus (Green-Riemann theorem), series,... He also contributed to

numerous physical problems (heat and light propagation, mag-

netism, hydrodynamics, acoustics, etc.).

unsuccessful, by a larger domain w hich is simply connected.

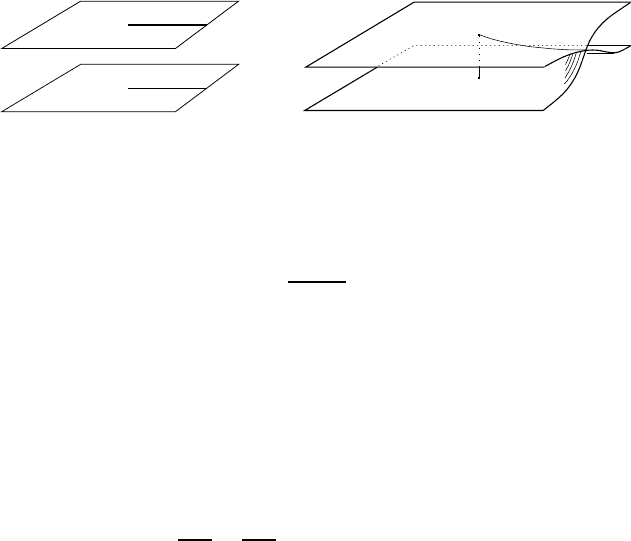
Denote by H the helix- shaped surface which is constructed as follows.

Take an inﬁnite collection of planes, stacked ver tically. Each of these planes

is then cut, for instance along the positive real axis, and the upper part of the

cut of one plane is then glued to the the lower part of the cut in the plane

immediately above:

cutting...

−−−−→

... and gluing

−−−−−−→

(The t hird ﬁgure is what is called a h elicoid in geometry. Here, only the

topology of the surface concerns us. The helicoid can be found in spiral

staircases. Close to the axis of the staircase, the steps are very steep; this is why

masons use an axis with nonzero radius.)

This surface is called th e Riemann s urface of the logarithm fu nction.

Each of the points on this surface can be mapped to a point on the complex

plane, simply by projecting vertically. Two points of the helicoid precisely

vertical to each other are therefore often identiﬁed to the same complex number.

They are distinguished only by being on a different “ﬂoor.” Note that walking

on the helicoid and turning once around the axis (i.e., the origin), means that

the ﬂoor changes, as in a parking garage.

PROPOSITION 5.8 H is simply connected.

It it then possible to deﬁne a logarithm function on H by integrating

the function ζ 7→ 1/ζ along a path on H joining 1 to z (1/ζ denoting

the inverse of the complex number identiﬁed with a point of the Riemann

surface). It is ea sy to see that this path integral makes sense and, because

of th is proposition, it does not depend on the choice of the path from 1

Harmonic functions 139

to z. This gives a well-deﬁned logarithm function L : H → C such that

exp(L(z)) = z for all points in H .

The point of view of a physicist is somewhat d ifferent. Instead of consid-

ering H , she is happy with C \ {0}, but says t hat the logarithm function is

multivalued, th at is, for a given z ∈ C \ {0}, the function L(z) takes not a

single value, but rather a whole sequence of values; the one that should be

chosen depends on the path taken to reach the point z. The function L is

then holomorphic on any simply connected subset of C\{0} (and t he classical

local results, such as the Taylor formulas, are applicable). It is also s aid that

the logarithm f unction has many branches (corresponding to a choice of the

ﬂoor of H ).

This viewpoint can seem quite shocking to the adepts of mathematical

rigor, but it has its advant ages and is particularly intuitive.

Next, let us construct the Riemann surface associated to the square-root

function. It is clear that by extending the square-root function by continuity

on C \{0}, the sign of the function changes after one turn around the origin,

but comes ba ck to its initial value after turning twice. Hence, we take two

copies of the complex plane, and cut them before gluing again in the following

manner:

gluing

−−−→

When the square-root function has a given value on one of the sheets, it

has the opposite value on the equivalent point of the other sh eet. However, it

should be noticed that this surface is not simply connected.

5.2

Harmonic functions

5.2.a Deﬁnitions

DEFINITION 5.9 (Harmonic function) A function u : R

→ R, deﬁned on an

open set Ω of the plane, is harmonic on Ω if its laplacian is identically zero,

that is, if it satisﬁes

△u =

∂

∂ x

∂

∂ y

= 0 at any point of Ω.

140 Complex Analysis II

We will see, in this section, that a number of theorems proved for h olomor-

phic functions remain true for harmonic functions, notably the mean value

theorem, and the maximum principle. This will have important consequences

in physics, w here there is an a bundance of harmonic functions.

First, w hat is the link between holomorphic functions and harmonic func-

tions?

If f ∈ H (Ω) is a holomorphic function, it can be expressed in the form

f = u + iv, where u and v are real-valued functions; it is then easy to show

that u and v are harmonic. Indeed, f being C

∞

, the functions u and v are

also C

∞

, so

△u =

∂

∂ x

∂

∂ y

∂

∂ x

∂ u

∂ x

∂

∂ y

∂ u

∂ y

Cauchy

∂

∂ x

∂ v

∂ y

−

∂

∂ y

∂ v

∂ x

Schwarz

= 0

from the Cauchy-Riemann equations on the one hand, and Schwarz’s theorem

concerning mixed derivatives of functions of class C

on the other hand. The

argument for v is similar. To summarize:

THEOREM 5.10 The real and the imaginary part of a holomorphic fu nction are

harmonic.

Now, we introduce t he notion of harmonicity for a complex-valued func-

tion. If f is C

we have

△f =

∂

∂ x

∂

∂ y



∂

∂ x

−i

∂

∂ y



∂

∂ x

+ i

∂

∂ y



f = 4

∂

∂ z

∂

∂ ¯z

f = 4 ∂∂ f .

DEFINITION 5.11 A complex-valued function f deﬁned on an open subset Ω

of the plane is ha rmonic if it satisﬁes

△f = 0, i.e., ∂∂ f = 0.

5.2.b Properties

PROPOSITION 5.12 A complex-valued function f is harmonic if and only if its

real and imaginary parts are harmonic.

Proof. If u and v are harmonic, then u + iv is cert ainly also harmonic since the

operators ∂ and ∂ are C-linear.

Conversely, if f is harmonic, it sufﬁces to take the real part of the relation △f = 0

to obtain △u = 0, and similarly for the imaginary part.

Hence, in particular, any holomorphic function is harmonic. What about

the converse? I t cannot hold in general because there need be no relation

whatsoever between the real and imaginary parts of a complex-valued h ar-

monic function, whereas there is a very subtle one for holomorphic functions

(as seen from the Cauchy-Riemann equations). However, there is some converse

for the real (or imaginary) part only:

Harmonic functions 141

THEOREM 5.13 Any real-valued harmonic funcion is locally the real part (resp. the

imaginary part) of a holomorphic function.

What is meant by “locally” here? Using only the methods of differential

equations, one can show that:

PROPOSITION 5.14 Let B be an open ball and f : B → R be a harmonic

function. There exists a harmonic function v : B → R such that F = u + iv is

holomorphic on B.

The astute reader will undoubtedly have already guessed what prevents

the extension of this theorem to any open subset Ω: if Ω has “holes,” the

function v may cha nge value wh en following its extensions around the hole.

The same phenomenon will be seen in the section about analytic continuation,

and it has already been visible in C auchy’s theorem. On the other hand, if u

is harmonic on a simply connected open subset, then u is indeed the real part

of a function holomorphic on the whole of Ω.

COROLLARY 5.15 If u : Ω → C is harmonic, then it is of class C

∞

Proof. It is enough to show that for any z ∈ Ω, there is some open ball B containing

z such that u restricted to B is C

∞

. But on B there is a ho l omorphic function f such

that u = Re( f ) on B; in partic u l ar, f is C

∞

on B, hence so is its real part in the sense

of R

-differentiability.

The following theorems are also d educed from Proposition 5.14.

THEOREM 5.16 (Mean value theorem) Let Ω be an open subset of R

≃ C and

let u be harmonic on Ω. For all z

∈ Ω and for all r ∈ R such that B(z

; r) ⊂ Ω,

we have

u(z

) =

2π

−π

u(z

+ r e

iθ

) dθ,

or, in real notation (on R

u(x

, y

) =

2π

−π

u(x

+ r cos θ, y

+ r sin θ) dθ.

THEOREM 5.17 (Maximum principle) Let Ω be a domain in C, u : Ω → R

a harmonic function and a ∈ Ω. Then eith er u is constant on Ω or a is not a

local maximum of u, that is, any neighborhood of a contains a point b such that

u(b) < u(a).

Similarly, if u is not constant, it does not have a local minimum either.

For ha rmonic functions, it is possible to explain the maximum principle

graphically. Indeed, if z is a local extremum (minimum or maximum), and is

not constant, the function u must have the following aspect:

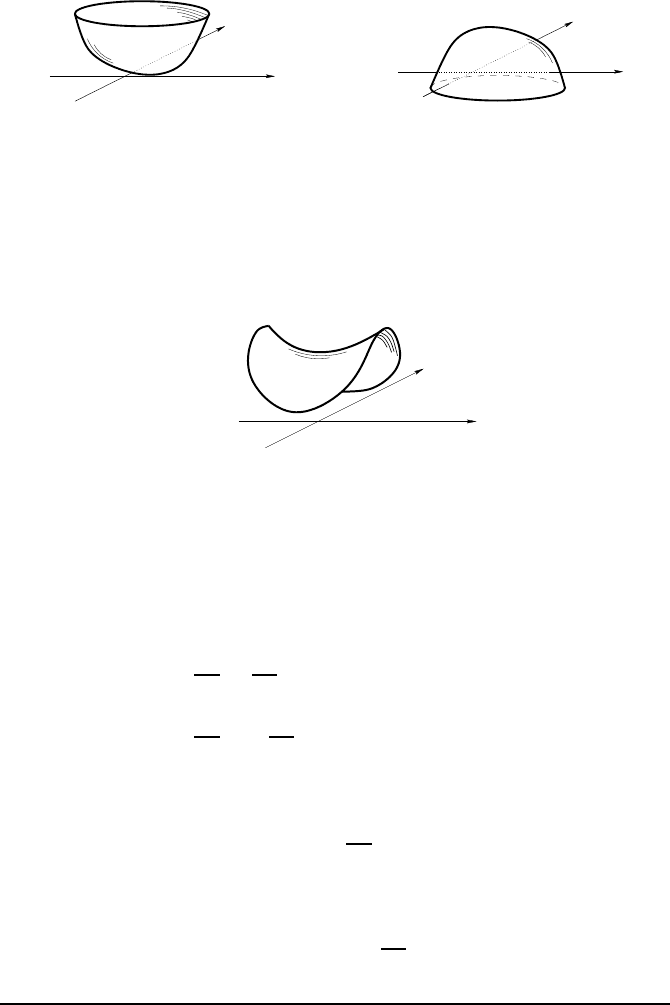
142 Complex Analysis II

But, in the ﬁrst case, it is transparent that ∂

u/∂ x

must be positive, as

well as ∂

u/∂ y

, and so the laplacian of u cannot be zero. In the second case,

those same partial derivatives are negat ive, and the laplacian cannot be zero

either.

A harmonic f unction must have one of the two partial derivatives negat ive

and the other positive, which gives the graph the shape of a saddle or a

mountain pass or a potato chip

Such a surface obviously has no local extremum, as any bicyclist will tell you!

5.2.c A trick to ﬁnd f knowing u

Consider a f unction u : Ω → R which is harmonic on a simply connected

open set Ω. To ﬁnd a function v : Ω → R which is also harmonic and such

that u + iv is holomorphic, we have to solve the system











∂ u

∂ x

∂ v

∂ y

∂ u

∂ y

= −

∂ v

∂ x

for any z ∈ Ω.

There is a classical method: integrating the second equation, we write

v(x, 0) = −

∂ u

∂ y

′

, 0) dx

′

then

v(x, y) = v(x, 0) +

∂ u

∂ x

(x, y

′

) dy

′

A question for physicists: why is it that a potato chip has a hyperbolic geometry? Another

question: why is it also true of the leaves of certain plants, and more spectacularly, for many

varieties of iris ﬂowers?

Harmonic functions 143

(integrating the ﬁrst equation).

In fact, a “trick” exists to ﬁnd easily the holomorphic f unction f with

real part equal to a given harmonic f unction u, avoiding the approach with

differential equations. Therefore let u be a h armonic function on a simply

connected open set Ω ⊂ C. We are looking for a holomorphic function

f : Ω → C such that u = Re( f ). Hence in particular

u(x, y) =

f (z) + f (z)

with z = x + i y

namely,

u(x, y) =

f (x + i y) + f (x + i y)

(∗)

We are considering the function u(x, y) as a function of two real variables.

Let us extend it to a function of two complex variables eu(z, z

′

). For instance,

if u(x, y) = 3x + 5x y, we deﬁne eu(z, z

′

) = 3z + 5zz

′

. Now put

g(z)

def

= 2eu





. (∗∗)

Then, using formulas (∗) and (∗∗), we get

g(z) = 2eu







+ i



+ f



−i

o

= f (z) + f (0), (5.3)

so that f (z) is, up to a purely imaginary constant, g(z) − g(0)/2, and hence

f (z) = g(z) −u(0, 0) + i C

To est ablish formula (5.3), we used t he fact that the function z 7→ f (z) ca n

also be expressed a s a certain function

f of the variable ¯z, and more precisely

as f (¯z). For instance, if f (z) = 3z + iz

, th en f (z) = 3¯z −i¯z

= f (¯z).

Now, isn’t all this a little bit ﬁshy? We have considered in the course of

this reasoning, that the functions (u, f ,...) behaved as “operators” performing

certain operations on their variables (raise it to a power, multiply by a con-

stant, take the cosine...), and that they could just as well perform them on a

complex variable if they could do so on a real one, or on ¯z if they knew how

to operate on z. T his is not at all the usual way to see a function! However, the

expansions of f and u in power series give a rigorous justiﬁcation of all those

manipulations. They also give the limit of t he meth od : it is necessary that the

functions have power series ex pansions valid on the whole set Ω considered.

Thus, this technique works if Ω is an open ball (or a connected and s imply

connected open subset, by analytic continuation), but not on a domain which

is not simply connected, an annulus, for example.

I wish to thank Michael Kiessling for teaching me this little-known trick.

144 Complex Analysis II

Example 5.18 Let u(x, y) = 3x

− 3 y

+ 5x y + 2, which satisﬁes △u = 0. Then we have

eu(z, ¯z) = 3z

−3¯z

+ 5z¯z + 2 and 2eu(z/2, z/2i) = 3z

+ 5z

/2i + 4 = f (z) + f (0), which gives

in particular that 2Re f (0) = 4, hence f (0) = 2+i×C

. Hence we have f (z) = 3z

+5z

/2i+ 2

(up to a purely imaginary constant) and one checks that th e real part of f is indeed equal to

Example 5.19 Consider the function u(x, y) = e

−x

sin y. It is easy to see that this f u nction

is harmonic. Then we have g(z) = 2e

−z/2

sin(z/2i) = −2ie

−z/2

sinh(z/2). Since g(0) = 0, we

have f (z) = g(z) + i C

, hence

−x

sin y = Re

2ie

−z/2

sinh



i

5.3

Analytic continuation

Assume a function f is known on an open subset Ω by a power series

expansion that converges on Ω. We would like to know it is possible to extend

the deﬁnition of f to a larger set.

Take a convenient example: we deﬁne the function f on the open ball

Ω = B(0 ; 1) by

f (x) =

∞

n=0

. (5.4)

We know that this power series is indeed convergent on Ω, but divergent for

|z| > 1. However, if we start from the point z

, for instance, we can

ﬁnd a new power series which converges to f on a certain neighborhood Ω

′

of z

f (z) =

∞

n=0

(z − z

)

on a neighborhood of z

. (5.5)

But — surprise! — this neighb orhood may well extend beyond Ω, as is shown

in Figure 5.2 on the facing page.

We can then choose a path γ and try to ﬁnd, for any point z of γ, a disk

of convergence of a power series centered at z coinciding with f on Ω. This

is what is called an analytic continuation a long a path (see Figure 5.3).

This means that it has been possible to continue the function f to certain

points of the complex plane where the original series (5.4) was not convergent.

On the intersection Ω

′

∩Ω, the two s eries (5.4) and (5.5 ) coincide, because of

the “rigidity” of holomorphic functions.

Is this rigidity sufﬁcient to ensure that this analytic continuation is unique?

Well, yes and no.

If we try to continue a function analytically by going around a singular ity,

the continuation thus obtained may depend on which side of the singularity

Analytic continuation 145

Ω

′

Fig. 5.2 — Analytic continuation of f on an open set Ω

′

extending beyond Ω.

Fig. 5.3 — Co ntinuation along a path γ with successive disks, and second continuation

along a path γ

′

146 Complex Analysis II

the ch osen pat h ta kes. For instance, in the case of th e function f deﬁned by

f (z) =

∞

n=1

(−1)

n+1

/n , which is equal to z 7→ log(1 + z) on Ω = B(0 ; 1),

there exists a singularity at the point z = −1. Two continuations, deﬁned by

paths running a bove or under the point z = 1, will differ by 2πi.

On the other hand, the following uniqueness result holds:

THEOREM 5.20 Let f be a function holomorphic on a domain Ω

. Let Ω

, . . . , Ω

be domains in C such that

i=1

Ω

is connected and simply connected and con-

tains Ω

. If there exists an analytic continuation of f to

i=1

Ω

, then this analytic

continuation is unique.

5.4

Singularities at inﬁnity

It is possible to compactify the complex plane by adding a single point at

inﬁnity.

DEFINITION 5.21 (Riemann sphere) We denote by C

def

= C ∪ {∞} the set

consisting of the complex plane together with an additional point “inﬁnity.”

The point a t inﬁnity corresponds to the limit “|z| → +∞” in C. Since

we add a single point, independent of the argument of z, t his means that

all the “directions” to inﬁnity are identiﬁed. Then we are led to represent

this extended complex plane in the form of a sphere,

called the Riemann

sphere. This can also be obtained, for example, by stereographic projection

(see Figure 5.4 on the next page).

DEFINITION 5.22 (Residue at inﬁnity) Let f be a function meromorphic on

the complex plane. Deﬁne a function F by F (z) = f (1/z). The function f

is said to have a pole at inﬁnity if F has a pole at 0, and f is said to have an

essential singula rity at inﬁnity if F has an essential singularity at 0.

The residue at inﬁnity of f , d enoted Res ( f ; ∞), is the quantity

Res ( f ; ∞) = Res



−

F (z) ; 0



One can understand why “a plane with all directions to inﬁnity identiﬁed is a sphere” by

taking a round tablecloth and grasping in one hand the whole circumference (the poi nts of

which are “inﬁnitely far” from the center for a physicist). One obtains a pou ch, which is akin

to a sphere.

The open sets in C are the usual open sets in C and the complements of compact subsets

in C. The topology obtained is the usual topology for the sphere, in which the point ∞ is like

any other point.