Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Application to the computation of horrifying integrals. . . 117

4.6

Applications to the computation of horrifying

integrals or ghastly sums

The goal of th is section is to show how the knowledge of Cauchy’s the-

orems and residues can help computing some integrals which are otherwise

quite difﬁcult to evaluate ex plicitly. In certain cases one can also evaluate the

sum of a series using similar techniques.

The idea, when trying to compute an integral on R, is to start with only

a piece of the integral, on an interval [−R, R], then close this path in the

complex plane, most of ten by a semicircle, checking that the added piece does

not contribute to the integral (at least in a suit able limit), and compute th is

new path integral by the Residue theorem. Before presenting examples, we

must establish conditions under which the “extra” piece of the integral will

indeed be negligible.

4.6.a Jordan’s lemmas

Jordan’s lemmas are lit tle theorems which are constantly useful when trying

to compute integrals using the meth od of residues.

The ﬁrst of Jordan’s lemmas is useful for th e comput ation of arbitrary

integrals.

THEOREM 4.84 (First Jordan lemma) Let f : C → C be a continuous function

in the sector

def



r e

iθ

; r > 0 and 0 ¶ θ

¶ θ ¶ θ

¶ π



such that lim

|z|→0

z f (z) = 0 (resp. lim

|z|→∞

z f (z) = 0).

Denote γ(r) =



r e

iθ

; θ

¶ θ ¶ θ



. Then we have

lim

r→0

γ(r)

f (z) dz = 0 (resp. lim

r→+∞

γ(r)

f (z) dz = 0).

118 Complex Analysis I

The second lemma is more speciﬁcally useful to compute Fourier trans-

forms.

THEOREM 4.85 (Second Jordan lemma) Let f : C → C be a continuous func-

tion on the sector

S =



r e

iθ

; r ¾ 0 and 0 ¶ θ

¶ θ ¶ θ

¶ π



such that lim

z→∞

z∈S

f (z) = 0. Then

lim

r→+∞

γ(r)

f (z) e

dz = 0.

Proof. Consider the case (the most dif ﬁcult) where the sector is 0 ¶ θ ¶ π. Remark-

ing that



ire

iθ



= e

−r sinθ

we can bound the integral under consideration by



γ(r)

f (z) e

i z



f (r e

iθ

)



r e

−r sinθ

dθ

π/2





f (r e

iθ

)



f (r e

i(π−θ)

)





r e

−r sin θ

dθ.

Let ǫ > 0. Since f is a function that tends to 0 at inﬁnity, there exi sts R > 0 such

that, for any r ¾ R and for any θ ∈ [0, π], we have



f (r e

iθ

)



¶ ǫ. In particular, for

any t ¾ R, we have



γ(r)

f (z) e

i z



¶ 2ǫ

π/2

r e

−r sin θ

dθ.

But for any θ ∈





, we have 0 ¶

2θ

¶ sin θ. We deduce that

π/2

r e

−r sin θ

π/2

r e

−2rθ/π

dθ =

(1 −e

−r

) ¶

which shows that for any r ¾ R, we have



γ(r)

f (z) e

i z



¶ πǫ.

4.6.b Integrals on RR

RR of a rational function

We consider the case where F is a rational function (i.e., a f unction of the

form F(x) = P (x)/ Q (x), where P and Q are two polynomials, which we

assume have no common zeros), and we wish to evaluate

F (x) dx. We will

assume here that the function F has no real pole, i.e., the polynomial Q does

not vanish on R (the situation where Q vanishes will be treated in Cha pter 8,

during th e study of Cauchy’s pr incipal values, page 223).

Application to the computation of horrifying integrals. . . 119

The nephew of the symbolist painter Puvis de Chavanne, Camille

Jordan (1838—1922), born in Lyons, was ﬁrst in the entrance exam

for the École Polytechnique at 17, then entered the École des

Mines and became engineer in charge of Parisian quarries. He

taught at the École Polytechnique, then entered Collège de France

and the Académie des sciences. He studied linear algebra, group

theory (he introduced the terminology abelian groups and stud-

ied cristallography; among his students were Felix Klein and So-

phus Lie), geometry, and Fourier analysis, and made some of the

ﬁrst steps in measure theory. He introduced some fundamental

topological concepts (homotopy). His pedagogical inﬂuence was

enormous.

We will also assume that the integral in question is indeed convergent,

which is the case if th e degrees of P and Q satisfy deg Q ¾ d eg P + 2.

We start by extending t he domain of the real variable to the comple x plane,

then tr uncate the integral on R to an integral on [−R, R], with R > 0, and

close the path of integration by means of a semicircle C

of radius R as in

Figure 4.4.

Denote by γ(R) = [−R, R] ∪ C

the contour thus deﬁned. According

to the assumptions, we can use t he ﬁrst of Jordan’s lemmas 4.84, with the

consequence that

F (z) dz −−−→

R→∞

0 and hence

lim

R→+∞

γ(R)

F (z) dz =

+∞

−∞

F (x) dx.

Moreover, when R goes to inﬁnity, the contour γ(R) ends up cont aining all

the poles of F in the upper half-plane, i. e. , for R large enough, we have

γ(R)

F (z) dz = 2πi

a pole in

upper half-pl ane

Res (F ; a),

which gives, in the limit R → +∞, the desired integral

+∞

−∞

F (x) dx = 2πi

a pole in

upper half-pl ane

Res (F ; a). (4.11)

Remark 4.86 We might, of course, have used a different contour in the argument to close the

segment [−R, R] in the lower half-plane. Then we would have had to compute the residues

in the lower half-plane. But then one would have had to be careful that with the orientation

chosen the winding number of the contour around each pole would be equal to −1 and not

−1, since the contour would have been oriented negatively.

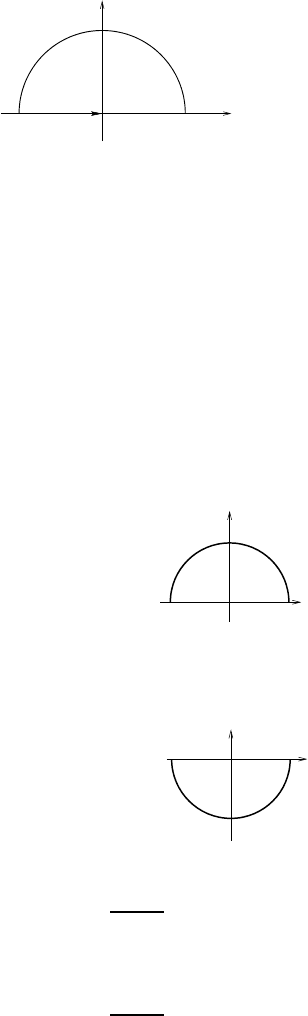
120 Complex Analysis I

R−R

Fig. 4.4 — Integration path for a rational function.

4.6.c Fourier integrals

We are looking here at evaluating integrals of the type

I =

+∞

−∞

f (x) e

ikx

dx with k ∈ R,

which occur very often in practice, since the y correspond to the value of the

Fourier transform of f evaluated a t k. One can use the same type of argument

and contour as the one used in Section 4.6.b, using this time t he second of

Jordan’s lemmas, but one must be c areful of the sign of k! Indeed, th e integral

on the upper semicircle

def



R e

iθ

; θ ∈ [0, π]



−R R

(4.12)

of f (z) e

ikz

only tends to 0 when r tends to inﬁnity when the real part of ikz

is negative; if z ∈ C

, we must then have k positive. If k is negative, we must

rather perform the integration along the lower semicircle

−

def



R e

−iθ

; θ ∈ [0, π]



−R R

(4.13)

Example 4.87 We try to compute

def

∞

−∞

cos(kx)

+ a

dx,

where a is a strictly positive real number. We start by writing the cosine in exponential form.

One way to do it is to use cos(kx) = (e

ikx

+ e

−ikx

)/2, but here it is simpler to notice that

J =

∞

−∞

ikx

+ a

dx,

the imaginary part being zero. For this last integral, we must now distinguish the two cases

k > 0 and k < 0.

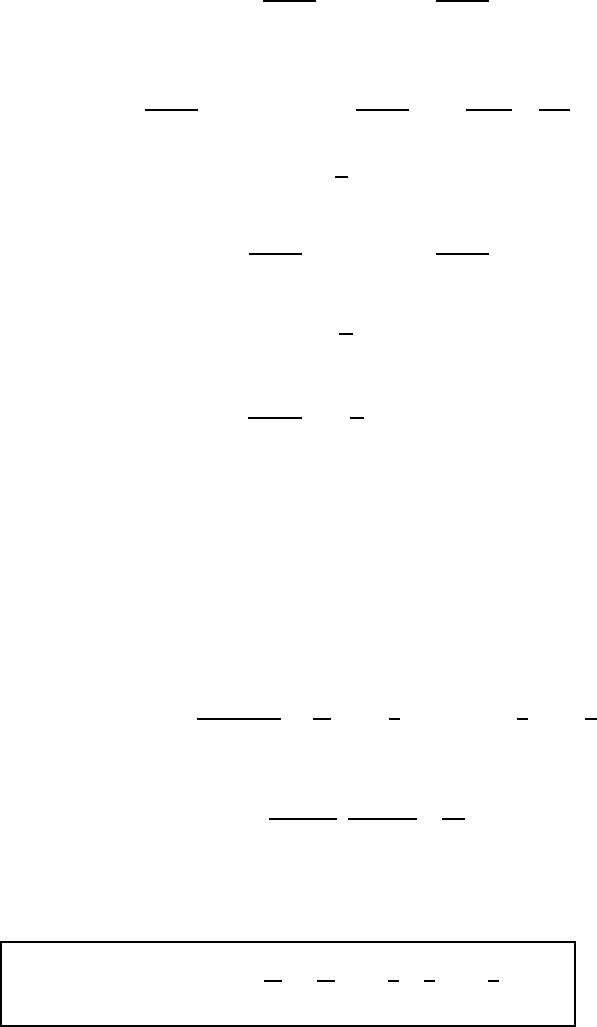
Application to the computation of horrifying integrals. . . 121

➀ When k > 0, we take the contour (4.12) and we obtain

J = lim

R→∞

(R)

ikz

+ a

dz = 2πi Res



ikz

+ a

; ia



since the only poles of the function being integrated are ia and −ia. These poles are

simple (because 1 /(z

+ a

) = 1/(z + ia)(z −ia)), and we compute easily

Res



ikz

+ a

; ia



= li m

z→ia

(z −ia)

ikz

+ a

= li m

z→ia

ikz

z + ia

−ka

2ia

which gives

J =

−ka

➁ When k < 0, we must take the contour (4.13) and we get

J = lim

R→∞

−

(R)

ikz

+ a

dz = −2πi Res



ikz

+ a

; −ia



We then evaluate t he residue at −ia, to obtai n

J =

To conclude, we have, independently of the sign of k (and even if k = 0)

∞

−∞

cos kx

+ a

dx =

−|k|a

4.6.d Integral on the unit ci r cle of a rational function

We are trying here to compute an integral of the type

K =

2π

R(sin t, cos t) dt,

where R(x, y) is a rational function which ha s no pole on the unit circle

+ y

= 1). Putting, naturally, z = e

, we obtain the relations

dz = ie

dt, sin t =

−e

−it



z −



, cos t =



z +



The integral becomes

K =



z −1/z

z + 1/z



where C is the unit circle with the positive orienta tion. An immediate appli-

cation of the Residue theorem shows that

K = 2πi

a pole ∈ B(0 ; 1)

Res







z −





z +





; a



(4.14)

122 Complex Analysis I

Example 4.88 We want to compute the following integral:

I =

2π

a + sin t

, a ∈ R, a > 1.

Put R(x, y) = 1/(a + x). Then we have

I = 2πi

a pôle ∈ B(0 ; 1)

Res

a +



z −



; a

Deﬁne now f (z)

def

= 2/(z

+ 2iaz −1), and it only remains to ﬁnd the poles of f . These are the

solutions of the equation z

+ 2iaz − 1 = 0, and so they are the po ints ζ = −ia + i

−1

and ζ

′

= −ia −i

−1. They are located as shown in the ﬁgure below

′

Only the pole ζ contributes to the integral, it is a simple pole with residue −i/

−1

and the integral is therefore equal to I = 2π/

−1.

4.6.e Computation of inﬁnite sums

Consider a series of t he form

S =

n∈Z

f (n),

where f is a given meromorphic function, decaying sufﬁciently rapidly for

the sum to exist, and with no pole on the real axis. One can check easily that

f (n) = Res



π f (z) cotan πz ; z = n



and s o

S =

n∈Z

f (n) =

n∈Z

Res



π f (z) cotan(πz) ; z = n



The partial sum from −N to N is therefore given by the integral of f along

the following contour

(where each circle is taken with positive orientation):

which we can deform (adding contributions which cancel each other in the

integral) into

Which is not a contour properly speaki ng since it consists of multiple pieces, but this is

without importance, the integral on this “contour” bei ng deﬁned as the sum of the integrals

on each circle.

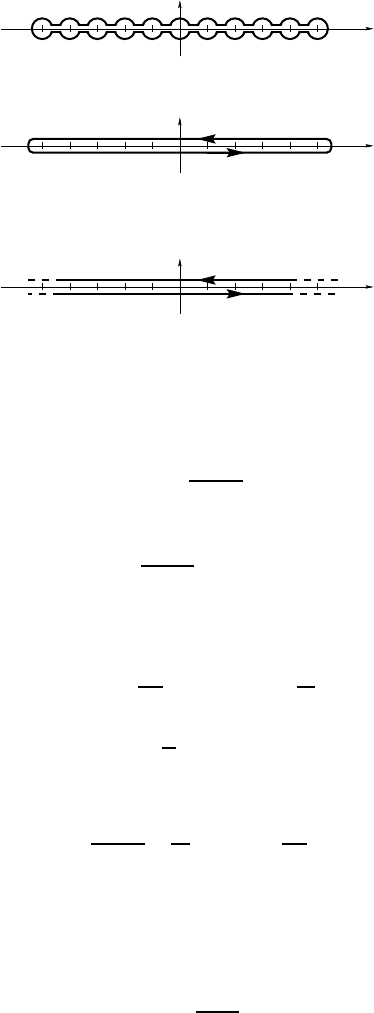
Application to the computation of horrifying integrals. . . 123

and by continuity into

In the limit where N tends to inﬁnity, and if the function f decays to 0, the

contour becomes simply

Finally, this last integral can be computed by the method of residues, by using

Jordan’s Lemmas and closing each of the lines by semicircles. There only

remains to evaluate the residues of the function f outside t he real axis.

Example 4.89 Suppose we want to evaluate the sum

S =

n∈Z

+ a

where a is a nonzero real number. We will then deﬁne

f (z)

def

+ a

π cotan(πz),

and S is the sum of the residues of this function at all the integers if a 6= 0. We will therefore

assume a > 0. The reasoning explained above shows that this sum is equal to t h e opp o site of

the sum of the residues of f at nonreal poles. These are located at z = ±ia, and we have

Res ( f ; z = ±ia) =

2ia

π cotan(iπa) = −

coth(πa),

hence the result

S =

coth(πa). (4.15)

One can note that, if a tends to 0, we have S ∼ 1/a

, whic h is th e expected behavior (the term

n = 0 of the sum is 1/a

). In the same manner, we have

∞

n=1

+ a

coth(πa) −

The meth od must obviously be tailored to each case, as the next example

shows:

Example 4.90 We now try to evaluate the sum

T =

∞

n=1

(−1)

Instead of using the function cotan, it is interesting to use the function z 7→ 1/ sin πz, which

has poles at every integer and for which the residue at n ∈ N is precisely equal to (−1)

/π.

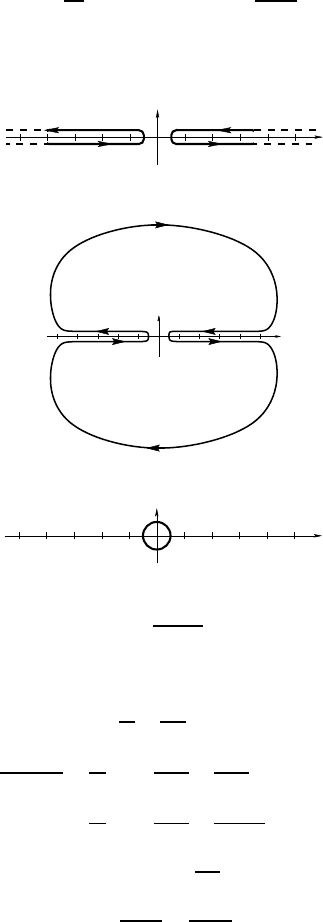
124 Complex Analysis I

Unfortu nately, the function z 7→ 1/z

has a pole at 0. This pole must th en be treated separately.

We start by noticing that

T =

′

with T

′

∞

n=−∞

n6=0

(−1)

and we deduce that the sum T

′

is given by 1/2i times the integral on the following contour

of the function z 7→ 1/z

sin(πz)

which we then close (appe al ing to Jordan’s second lemma) into

before deforming it by continuity into

which gives

′

= −Res



sin z

; z = 0



the minus sign coming from the fact that the last path is taken with negative orientation. There

only remains to evaluate this residue, using, for instance, a Taylor expansion of 1/ sinπz:

sin z = z −

120

+ ··· ,

sin πz



1 −

120

+ ···



−1



1 +

14π

720

+ ···



which shows that the residue of 1/z

sin πz at 0 is

14π

720

and that

∞

n=1

(−1)

−7π

720

Exercises 125

EXERCISES

 Exercise 4.4 Show that if f is holomor phic on an open subset Ω ⊂ C, then

△



|f |



= 4



∂ f

∂ z



 Exercise 4.5 Let f and g be continuously differentiable functions on R

identiﬁed with C

(i.e., functions suc h that t he part ial derivatives ∂ f /∂ x and ∂ f /∂ y e xist and are c ontinuous).

Show th at the following chain rules hold:

∂

∂ z

( f ◦ g) =

∂ f

∂ z

∂ g

∂ z

∂ f

∂¯z

∂ g

∂¯z

and

∂

∂ ¯z

( f ◦ g) =

∂ f

∂ z

∂ g

∂ ¯z

∂ f

∂ ¯z

∂ g

∂ z

 Exercise 4.6 Let U be a connected open set and let f : U → C be a function such that f

and f

are holomorphic. Show that f is holomorphic on U .

Path integration

 Exercise 4.7 Consider, in C, the segments T

= [−i, 6 i], T

= [−i, 2 + 6i] and T

[2 + 5i, 6i]. Deﬁne now a function f : C → C by f (x + i y) = x

−3i y. Compute explicitly

f (z) dz and

∪T

f (z) dz. Conclude.

 Exercise 4.8 Denoting by T th e circular arc joining 3 to i

3 with equation

(x −1)

+ y

= 4,

compute

dz/z

 Exercise 4.9 Recall that

+∞

−∞

−x

dx =

π. One then wishes to compute, for any nonzero

a ∈ R, the integral

+∞

−∞

−x

cos(ax) dx.

Let f (z) = e

−z

for any z ∈ C, and denote by T the rectangle

T = [−R, R, R + ia/2, −R + ia/2].

Compute the integral

f (z) dz and conclude by letting R go to inﬁnity.

Integrals using residues

 Exercise 4.10 Compute the residue at 0 of sin(z)/z

 Exercise 4.11 Prove the convergence of the following integrals and compute their values:

+∞

−∞

(1 + x) sin 2x

+ 2x + 2

dx and

+∞

−∞

(1 + x

)

with n ∈ N

∗

126 Complex Analysis I

 Exercise 4.12 (Fresnel integral) Does the Fresnel integral

def

+∞

−∞

i x

exist in the sense of Lebesgue?

We neverthe less try to assign a meaning to this i ntegral. Show that

I (R, R

′

)

def

′

−R

i x

exists and has a limit as R and R

′

go to +∞, and compute this limit , using a suitable contour

and remembering th e following value of the gaussian integral:

+∞

−∞

−x

dx =

π.

 Exercise 4.13 (Fourier transf orm of the gaussian) Let ν ∈ R. Compute

+∞

−∞

−πx

−2iπν x

dx,

which is the Fourier transform of the g au ssian x 7→ e

−πx

at the point ν. One may use

Exercise 4.9.

(Another method will be given in Exercise 10.1 on page 295, using the Fourier transform.)

 Exercise 4.14 Let A be a ﬁnite subset of C containing no po sitive real number. Let µ ∈

C \ Z. Let ﬁnally f : C → C be a function meromorphic on C and holomorphic on C \ A,

such that

lim

r→0

or r→+∞

= 0 with I

def

2π



f (r e

iθ

)



−Reµ+ 1

dθ.

Show that we have t h en

+∞

f (x) x

−µ

dx =

2iπ

1 −e

2iπµ

a∈A

Res



f (z) e

−µL(z)

; a



where L denotes the complex logarithm deﬁned on C \R

L (z)

def

= log |z|+ iθ(z) with θ(z) ∈ ]0, 2π[ .

 Exercise 4.15 Let f be a funct ion holomorphic in the open disc D(0; R) with R > 1.

Denote by γ the unit circle: γ

def



iθ

; θ ∈ [0, 2 π[



Computing in two different ways the integrals

I =



2 +



z +



f (z)

dz, J =



2 −



z +



f (z)

dz,

show that











2π



iθ



cos





dθ = 2 f (0) + f

′

(0),

2π



iθ



sin





dθ = 2 f (0) − f

′

(0).