Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Cauchy’s theorem 97

Proof. Indeed,

′

(z) dz = F



γ(b)



− F



γ(a)



= 0 since γ is a closed path so

γ(b) = γ(a).

In particular we deduce the following result.

THEOREM 4.30

For

any closed path γ and any n ∈ N

any closed path γ, 0 /∈ γ and n = −2, −3, . . .

, we have

dz = 0.

Proof. For any n ∈ Z, n 6= −1, the function z 7→ z

is the derivative of

z 7→

n+1

(n + 1)

which is holomorphic on C if n ¾ 0 or on C \ {0} if n ¶ −2. The preceding

proposition gives the conclusion.

This property is very important, and will be used to prove a number of

results later on. An important point: the (excluded) case n = −1 is very

special. We have sh own (see formula (4.4)) that the integral of 1/z along at

least one closed path is not zero. This comes from the fact that the function

z 7→ 1/z is the only one among the functions z 7→ 1/z

which is not the

derivative of a function holomor phic on C

∗

. It is true that we will deﬁne a

“logarithm function” in th e complex plane, with der ivative equal to z 7→ 1/z,

but we w ill see (Section 5.1.a on page 135) that this “ complex logarithm” can

never be deﬁned on the whole of C

∗

, but only on smaller domains where it is

not possible for a closed path to turn completely around 0.

Here is now a ﬁrst version, somewha t restr icted, of Cauchy’s theorem.

PROPOSITION 4.31 (Cauchy’s theorem for triangles) Let ∆ be a closed trian-

gle in the plane (by this is meant a “ﬁlled” triangle, with boundary ∂∆ consisting

of three line segments), entirely contained in an open set Ω. Let p ∈ Ω and let

f ∈ H



Ω \ {p}



be a function continuous on Ω and holomorphic on Ω except

possibly at the point p. Then

∂∆

f (z) dz = 0.

Proof. The proof, elementary but clever, is well worthy of attention. Because of its

length, we have put it in Appendix D.

Remark 4.32 We have added some ﬂexibility to the statement by allowing f not to be holo-

morphic at one point (at most) in the triangle. In fact, this extra generality is illusory. Indeed,

we will see further on that if a f u nction is holomorphic in an open subset minus a singl e

point, but is continuous on the whole open set , then in fact it is holomorphic everywhere on

the open set .

The following version is much more useful.

98 Complex Analysis I

THEOREM 4.33 (Cauchy’s theorem for convex sets) Let Ω be an open convex

subset of the p lane and let f ∈ H (Ω) be a function holomorphic on Ω. Then, for

any closed path γ contained in Ω,

f (z) dz = 0.

Proof. Fix a point a ∈ Ω and, for all z ∈ Ω, deﬁne, using the convexity property,

F (z)

def

[a,z]

f (ζ ) dζ ,

where we have denoted

[a, z]

def



(1 −θ)a + θz ; θ ∈ [0, 1]



We now show that F is a primitive of f .

 Let z

be a point in Ω. For any z ∈ Ω, the triangle ∆

def

= 〈a, z, z

〉 is contained in Ω.

Applying Cauchy’s Theorem for a triangle, we get that

,z]

f (z) dz = F (z) − F (z

hence

F (z) − F (z

)

z − z

− f (z

) =

z − z

,z]



f (ζ ) − f (z

)



dz −−→

z→z

using the continuity of f . The function F is therefore differentiable at z

and its

derivative is given by F

′

) = f (z

).  .

We have proved that f = F

′

. Proposition 4.29 the n ensures that the integral of f

on any closed path is zero.

Finally, there exists an even more general version of the theorem, which is

optimal in some sense. It requires the notion of a simply connected set (see Def-

inition A.10 on page 575 in Appendix A). The proof of this is unfortunately

more delicate. However, the curious reader will be able to ﬁnd it in any good

book devoted to complex analysis [43,59].

THEOREM 4.34 (Cauchy’s theorem for simply connected sets) Let Ω be a sim-

ply connected open subset of the plane and let f ∈ H (Ω). Then for any closed γ

inside Ω,

f (z) dz = 0.

Remark 4.35 In fact, one can show that if f ∈ H (Ω), where Ω is an open si mply connected

set (as for instance a convex se t), then f admits a primitive on Ω. The vanishing of the integral

then follows as before.

In the case of an open s et with holes, one can us e a generalization of

Cauchy’s theorem. It is easy to see that s uch an open set can be dissected in a

manner similar to w hat is indicated in Figure 4.1. One takes the convention

that the boundary of the holes is given the negative (clockwise) orientation,

and the exterior boundary of the open set is given the positive orienta tion.

The integral of a holomorphic function along the boundary of t he open set,

with this orientation, is zero.

Properties of holomorphic functions 99

Ω Ω

′

∂Ω ∂Ω

′

Fig. 4.1 — One can dissec t an open se t having one or more “holes” to make it simply

connected. The integ ral on the boundary ∂Ω

′

of the new open set thus deﬁned

is zero since Ω

′

is simply connected, which shows that the integral on ∂Ω (with

the orientation chosen as described on th e left) i s also zero.

4.2.e Application

One consequence of Cauchy’s theorem is th e following: one can move the

integration contour of an holomorphic function continuously without chang-

ing the value of the integral, under the condition at least that the function

be holomorphic at all the points which are swept by th e path during its

deformation.

THEOREM 4.36 Let Ω be an open subset of C, f ∈ H (Ω), a nd γ a path in Ω. If

γ can be deformed continuously to a path γ

′

in Ω, then

f (z) dz =

′

f (z) dz.

Proof. The proof is somewhat delicate, but one can give a very intuitive graphical

description of the idea. Indeed, one moves from t h e contour γ in Figure 4.2 (a) to the

contour γ

′

of Figure 4.2 (b) by adding the contour of Figure 4.2 (c). But the latter does

not contain any “hole” (since γ is deformed co ntinuously to γ

′

); therefore the integral

of f on the last contour is zero.

4.3

Properties of holomorphic functions

4.3.a The Cauchy formula and applications

THEOREM 4.37 (Cauchy’s formula in a convex set) Let γ be a closed path in a

convex open set Ω and let f ∈ H (Ω). If z ∈ Ω and z /∈ γ, we have

f (z) ×Ind

(z) =

2πi

f (ξ )

ξ − z

dξ.

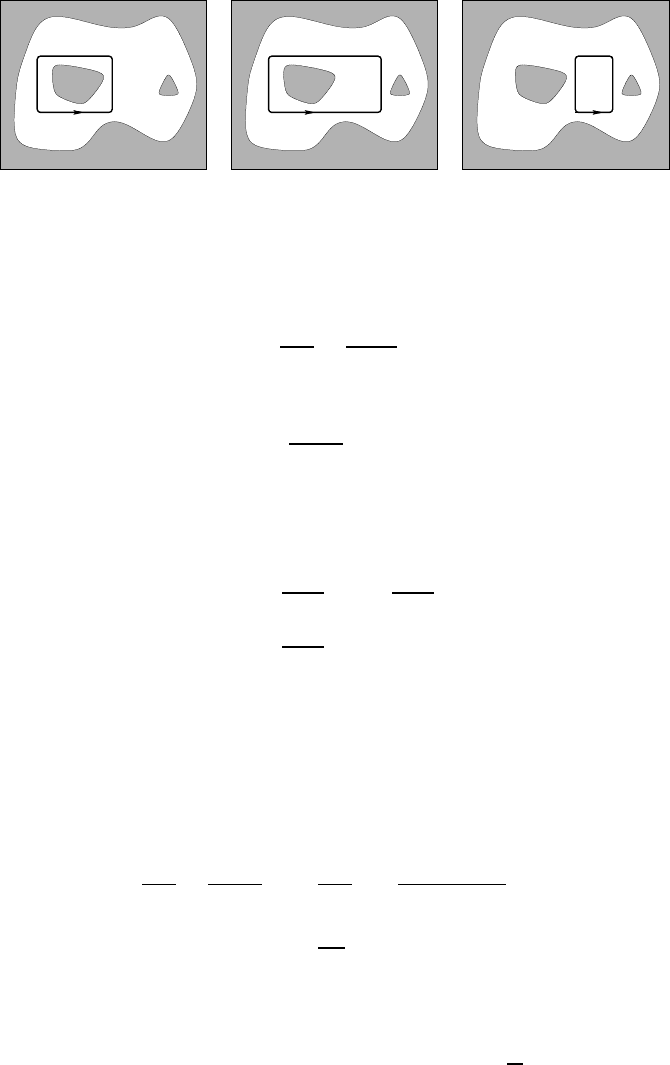
100 Complex Analysis I

(a) (b) (c)

Fig. 4.2 — The three contours γ, γ

′

et γ

′

−γ.

In particular, if γ turns once around z counterclockwise, then

f (z) =

2πi

f (ξ)

ξ − z

dξ.

Proof. Let z ∈ Ω, z /∈ γ and deﬁne a function g by

g(ξ)

def

f (ξ)−f (z)

ξ−z

if ξ ∈ Ω, ξ 6= z,

′

(z) if ξ = z.

Then g ∈ H (Ω \ {z}) and is continuous at z; it is then possible to show (see The-

orem 4.56) that g is h ol omorphic on Ω. So, by Cauchy’s theorem for a convex set,

g(ξ) dξ = 0, hence

0 = −

f (ξ)

ξ − z

dξ +

dξ

ξ − z

× f (z)

= −

f (ξ)

ξ − z

dξ + 2πi Ind

(z) f (z)

by deﬁniti o n of the winding number of a path around a point.

Remark 4.38 This result remains valid for a simply connected set.

Let us apply this theorem to the case, already mentioned, where th e path

of integration is a circle centered a t z

with radius r: γ = C (0 ; r). One can

then parameterize γ by z = z

+ re

iθ

and we have

f (z

) =

2πi

f (z)

z − z

dz =

2πi

−π

f (z

+ re

iθ

)

r e

iθ

rie

iθ

dθ

2π

−π

f (z

+ re

iθ

) dθ,

which allows us to write:

THEOREM 4.39 (Mean value property) If Ω is an open su bset of C and if f is

holomorphic on Ω, then for any z

∈ Ω and any r ∈ R such that B(z

; r) ⊂ Ω, we

Properties of holomorphic functions 101

have

f (z

) =

2π

−π

f (z

+ re

iθ

) dθ.

This theorem links the value at a point of a holomor phic function with

the average of its values on an arbitrary circle centered at this point, which

explains the name.

Here now is one the most fundamental results from the theoretical view-

point; it also has practical implications, as we will see in Chapter 15 about

Green functions.

THEOREM 4.40 (Cauchy formul a s) Let Ω be an open subset of C and let f :

Ω → C be an arbitratry function. We have

f ∈ H (Ω) ⇐⇒ f is analytic on Ω.

Moreover, for any n ∈ N and for any a ∈ Ω,

(n)

(a) =

2πi

f (z)

(z −a)

n+1

dz,

where γ is any path inside Ω such that Ind

(a) = 1.

Recall that f is analytic on an open subs et Ω if and only if, a t any point

of Ω, f admits locally a power series expansion converging in an open disc

with non-zero radius. Th e proof will use Cauchy’s Formula:

Proof. ◮ Let us prove the implication ⇐ . If th e power series f (z) =

∞

n=0

(z −

converges on an open ball with radius r > 0 around the poi nt a, then according

to Theorem 1.69, the series

(z −a)

n−1

converges on the same op en ball. Without

loss of generality, we can work with a = 0. Denote

g(z)

def

∞

n=0

n−1

, z ∈ B(0 ; r).

We now show that we have indeed f

′

= g on B(0 ; r) .

 Let w ∈ B(0 ; r). Choose a real numer ρ such th at |w| < ρ < r. Let z 6= w be a

complex number. We have

f (z) − f (w)

z − w

− g(z) =

∞

n=1



− w

z − w

−nw

n−1



The term between brackets is zero for n = 1. For n ¾ 2, it is equal to



− w

z − w

−nw

n−1



= (z − w)

n−1

k=1

k−1

n−k−1

(To prove this formula, it sufﬁces to express the right-hand side using the well-known

relation 1 − x

= ( 1 − x)

n−1

k=0

, putting x =

or x =

.) Hence, if |z| < ρ,

the modulus of the term between brackets is at most equal to n(n −1)ρ

n−2

/2, and



f (z) − f (w)

z − w

− g(z)



¶ |z − w|

∞

n=1

|ρ

n−2

102 Complex Analysis I

But this last series is convergent (Theorem 1.69). Letting z tend to w, we ﬁnd that f is

differentiable at w and that g(w) = f

′

(w). 

So it follows that f is holomorphic on B(a ; r) , and its derivative admits a power

series expansion of the type f

′

(z) =

n¾1

(z − a)

n−1

. By induction one can even

show that the successive derivatives of f are given by the formula in Theorem 1.69 on

page 35, which is therefore valid for complex variables as well as for real variables.

◮ Let us prove the implication ⇒. We assume then that f ∈ H (Ω).

 Let a ∈ Ω, and let us show t h at f admits a power series ex pansion around a.

Since Ω is open, one can ﬁnd a real number R > 0 such that B(a ; R) ⊂ Ω. Let γ be

a circle centered at a and with radius r < R. We have (Theorem 4.37)

f (z) =

2πi

f (ξ )

ξ − z

dξ z ∈ B(a ; r).

But, for any ξ ∈ γ, we have



z −a

ξ −a



|z −a|

< 1;

hence the geometric series

∞

n=0

(z − a)

(ξ −a)

n+1

ξ − z

converges uniformly with respect to ξ on γ, and this for any z ∈ B (a ; r), which allows us

to exchange the series and the integral and to write

f (z) =

2πi

∞

n=0

(z − a)

(ξ −a)

n+1

f (ξ ) dξ =

2πi

∞

n=0

(z −a)

f (ξ )

(ξ −a)

n+1

dξ

∞

n=0

(z − a)

with

def

2πi

f (ξ)

(ξ −a)

n+1

dξ.

So we have shown that f admits a power series expansion around a. Moreover we now

(see the general theory of power seri es) that in fact we have c

= f

(n)

(a)/n!, and this

gives the formula of the the o rem. 

In conclusion, f is indeed analytic on Ω and the formula is proved.

An immediate consequence of this theorem is:

THEOREM 4.41 Any function holomorphic on an open set Ω is inﬁnitely differen-

tiable on Ω.

We can now pause to review our trail so far. We have ﬁrst deﬁned a

holomorphic function on Ω as a function differentiable at any point of Ω.

Having a single derivative at any point turns out to be sufﬁcient to prove

that, in fact, f has derivatives of all order, which is already a very strong

result. Even stronger is that f is analytic on Ω, that is, that it can be expanded

in power series around every point. And the proof shows something even

beyond this: is we take a point z ∈ Ω, and any open ball centered at z entirely

Properties of holomorphic functions 103

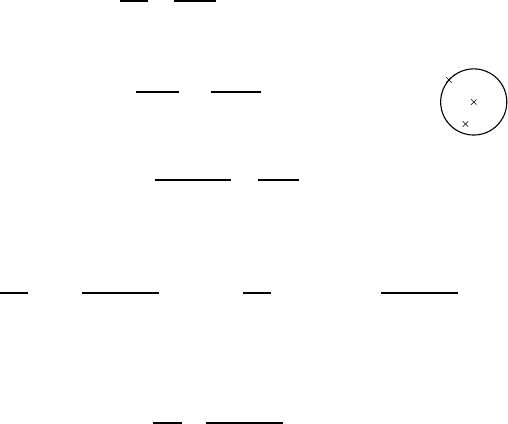
Ω

Fig. 4.3 — If f is holomorphic on Ω, then f has a power seri es expansion converging on

the gray open ball (the open ball with largest radius contained in Ω).

contained in Ω, then f can be expanded in a power series that converges on

this ball

(see Figure 4.3). In particular, we have t he following theorem.

THEOREM 4.42 Let f be a function holomorphic on the w hole of C. Th en f admits

around any point a power series expansion that converges on the whole complex plane.

Example 4.43 The function z 7→ exp(z) has, around 0, the power series expansion given by

∞

n=0

with inﬁnite radius of convergence. Around a point z

∈ C, the function has (another)

expansion

∞

n=0

(z − z

)

which converges also on the whole of C.

DEFINITION 4.44 An entire function is any function which is holomorphic

on the whole complex plane.

The following theorem is due to Cauchy, but bears the name of Liouville

THEOREM 4.45 (Liouville) Any bounded entire function is constant.

This th eorem tells us that any entire function which is not const ant must

necessarily “tend to inﬁnity” some w here. This “somewhere” is of course “at

inﬁnity” in the complex plane, but one must not think that it means that

“ f (z) tends to inﬁnity when |z| tends to inﬁnity. ” For instance, if we consider

the function z 7→ exp(z), we see that if we let z tend to inﬁnity on the left

There can of c o u rse be convergence even outside this ball; this brings the possibility of

analytic continuation (see Section 5.3 on page 144).

Not because it was thought that Cauchy already had far too many theorems to his name

but because, Liouville having quoted it during a lecture, a German mathemati cian attributed

the result to him by mistake; as sometimes happens, the mistake took hold.

104 Complex Analysis I

Joseph Liouville (1809—1882), son of a soldie r and student at

the École Polytechnique, became professor there at the age of 29,

a member of the Académie des Sci ences at 30 and a professor

at the Collège de France at 42. A powerful and eclectic mind,

Liouville studied with equal ease geometry (surfaces with constant

curvature), number theory (constructing the ﬁrst transcendental

number, which bears his name), mechanics (three-body problem,

celestial dynamics,...) analysis,... and he became actively involved

in the diffusion of mathematic s, creating an important journal,

the Journal de mathématiques pures et appliquées, in 1836.

side of the plane (that is, by letting the real part of z go to −∞), then exp(z)

tends to 0. It is only if the real part of z tends to +∞ that |e

| tends to

inﬁnity.

Proof of Liouville’s theorem. We star t by recalling the following result:

LEMMA 4.46 If f is an entire function such that f

′

(z) ≡ 0 on C, then f is constant.

According to the Cauchy formulas (Theorem 4.40), if γ is a contour turning once

around z in the positive direction, we have

2πi

f (ζ )

(ζ − z)

dζ = f

′

(z).

If we assume that f is bounded, there exists M ∈ R such that



f (z)



< M for

any z ∈ C.

Let then z ∈ C, and let us show that f

′

(z) = 0.

 Let ǫ > 0. Consider the circle γ centered at z and with arbitrary radius R > 0.

We have



′

(z)



2πi



f (ζ )

(ζ − z)

dζ



2π



f (ζ )



|ζ − z|

dζ ¶

If we select the radius R so that R ¾ M /ǫ (which is always possible since the function

f is deﬁned on C), we obtain therefore



′

(z)



¶ ǫ. 

As a consequence, we have found that f

′

(z) = 0. This being true for any z ∈ C, the

function f is constant.

4.3.b Maximum modulus principle

THEOREM 4.47 (Maximum modulus principle) Let Ω be a domain in C, f a

function holomorphic on Ω, and a ∈ Ω. Then, either f is constant, or f has no local

maximum at the point a, which means that any neighborhood of a contains points b

such that



f ( a)



f (b)



What does this result mean? At any point in the open s et of deﬁnition,

the modulus of the holomorphic function cannot have a local maximum. It

can have a minimum: it sufﬁces to consider z 7→ z w hich a local (in fact,

global) minimum a t z = 0. But we can never ﬁnd a maximum.

Properties of holomorphic functions 105

COROLLARY 4.48 Let f ∈ H (Ω) and let V be a bounded open subset of Ω, such

that the closure V of V is contained in Ω. Then the supremum of f on V is achieved

on the boundary of V , which means that there exists w ∈ ∂ V such that



f (w)



= sup

z∈V



f (z)



We will see later tha t this theorem also applies to real harmonic functions

(such as the electrostatic potential in a vacuum), which will have important

physical consequences (see Chapter 5; it is in fact there that we will give,

page 141, a graphical interpretation of the maximum modulus principle).

4.3.c Other theorems

We write down for information a theorem which is the converse of Cauchy’s

theorem for triangles:

THEOREM 4.49 (Mor er a ) Let f be a complex-valued function, continuous on an

open su bset Ω of C, such that

∂∆

f (z) dz = 0

for any closed triangle ∆ ⊂ Ω. Then f ∈ H (Ω).

This theorem has mostly historical importance, and some interest for pure

mathemat icians , but is of little use in physics. It is only stated for the reader’s

general knowledge.

On the other hand, here is a theorem which is much more useful, due to

Green

THEOREM 4.50 (Gr een-Riemann) Let P and Q be functions from R

to R or

C, R

-differentiable, and let K be a sufﬁciently regular compact subset.

Then we have

∂ K

(P dx + Q d y) =



∂ Q

∂ x

−

∂ P

∂ y



dx dy.

George Green (1793—1841), Eng lish mathematician, was born and died in Nottingham,

where he wasn’t sheriff, but rather miller (the mill is still functional) and self-taug ht. He

entered Cambridge at 30, where he got his doctorate four years later. He studied potential

theory, proved th e Green-Riemann formula, and developed an English school of mathematical

physics, followed by Thompson (discoverer of the electron), Stokes (see page 472), Rayleigh,

and Maxwell.

The boundary of K , denoted ∂ K, must be of class C

and, for any point z ∈ ∂ K , there

must exist a neigh borhood V

of z homeomorphic to the unit open ball B(0 ; 1), such that

∩ K corresponds by the homeomorphism with the upper half-plane. This avoids a number

of pathologies.

106 Complex Analysis I

This result can be stated in the language of functions on C in the following

manner.

THEOREM 4.51 (Gr een) Let F (z, ¯z) be a func tion of the variables z and ¯z, ad-

mitting continuous pa rtial derivatives with respect to each of them, and let K be a

sufﬁciently regular compact subset of C. Then we have

∂ K

F (z, ¯z) dz = 2i

∂ F

∂¯z

dA,

where dA denotes the area integra tion element in the complex plane. One can also

write F as a function of x a nd y, which gives us (with a slight a bu se of notation)

∂ K

F (x, y) dz = 2i

∂ F

∂¯z

dx dy.

Proof. It is enough to write F = P + i Q and to apply the formula from Theo-

rem 4.50 to the real and to the imaginary parts of

∂ K

F dz.

The Green-Riemann formula sh ould be compared with the Stokes for-

mula

for differential forms, given page 473.

4.3.d Classiﬁcation of zero sets of holomorphic functions

The rigidity of a h olomorphic function is such that, if one knows the values

of f in a very small subset of t he open set of deﬁ nit ion Ω, then these data

are t heoretically sufﬁcient to know f on the whole of Ω (see Exercise 4.1

on page 90). What amount of information actually sufﬁces to determine f

uniquely? The answer is g iven by the following theorem: a sequence of points

having one accumulation point in Ω is enough.

First we recall the d eﬁnition of an accumulation point.

DEFINITION 4.52 Let Z be a subset of C. A point c ∈ Z is an accumula tion

point if there exists a sequence (z

)

n∈N

of elements of Z\{c} such that z

→ c.

(It is important to remark that the deﬁnition imposes that z

6= c for all

n ∈ N; without this condition, any point would be an accumulation point, a

constant sequence equal to c converging always to c.)

THEOREM 4.53 (Classiﬁcation of zero sets) Let Ω be a domain of C (recall that

this means a connected open set) and let f ∈ H (Ω). Deﬁne the zero set of f by

Z( f )

def



a ∈ Ω ; f (a) = 0



An approach to complex analysis based on differential forms is presented by Dolbeault

in [29]. It is a more abstract vie wpoint at ﬁrst sig h t, but it is very rich.