Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Exercises 127

 Exercise 4.16 Compute the value of

+∞

+ 1

On may use the classical contour or, more cleverly, a sector with angle π/3.

 Exercise 4.17 Compute

∞

log x

1 + x

dx.

 Exercise 4.18 Compute

∞

cos



πx



−1

dx.

 Exercise 4.19 Show that

+∞

sin x

dx =

+∞

cos x

dx =

Hint: Use the following contour: from 0 to R on the real axis, then an eighth of a ci rcle

up to R e

iπ/4

, and then back to the starting point along th e imaginary axis.

 Exercise 4.20 Show that

+∞

cosh ax

cosh x

dx =

2 cos





, where |a| < 1.

Hint: Look for the poles of F (z) =

cosh z

, and c o nsider the contour integral on the

rectangle with vertices at [−R, R, R + iπ, −R + iπ].

 Exercise 4.21 Show that if R is a rational function without poles on the half-axis of posit ive

real numbers R

, if α ∈]0, 1[ and if R(x)/x

is integrable on R

, then



1 −e

−2iπα



+∞

R(x)

dx = 2iπ

poles other

than z = 0

Res



R(z)



where the function z 7→ z

is deﬁned by ρ e

iθ

7→ ρ

iαθ

for all θ ∈ [0, 2π[.

Hint: Use the following contour and take

the limits [R → +∞] and [ǫ → 0].

 Exercise 4.22 Show that if α ∈ ]0, 1[, then

+∞

(1 + x)

sin πα

128 Complex Analysis I

 Exercise 4.23 Let a be a positive real number. Compute then

lim

ǫ→0

+∞

−∞

−a

−iǫ)

Hint: Take the following contour and the

limit [R → +∞].

a−a

Sums using residues

 Exercise 4.24 Compute the following two series:

S =

n∈N

∗

+ a

and T =

n∈N

∗

+ a

with a ∈ R, a ¾ 0.

 Exercise 4.25 (Ramanujan’s formula) Using the function z 7→ cotan πz, deduce, by means

of a cle ver contour, that

coth π

coth 2π

+ ···+

coth nπ

+ ··· =

19π

56 700

Note: This beautiful formula is due to the great indian mathematician Ramanujan.

But

Ramanujan did not use the calculus of residues.

PROBLEM

 Problem 2 Application to ﬁnite temperature ﬁeld theory — In quantum statistical me-

chanics, some quantities at equilibrium (such as the density of a gas, its pressure, its average

energy) are computed using sums over discrete frequencies (called Matsubara frequencies).

We consider here a simple case where these sums are easily computable using the met h od of

residues.

For instance, if one considers a gas of free (i.e., noninteracting) electrons (and positrons

denote by µ the chemical potential of the electrons; the positrons have chemical potential

equal to −µ. The temperature being equal to T , put β = 1/k

T , where k

is the Boltzmann

constant.

The free charge density, in momentum spac e, is given [55, 60] by

N ( p)

def

4(iβω

+ βµ)

(iβω

+ βµ)

−β

Srinivasa Ramanujan (1887—1920) was probably the most romantic character in the math-

ematical pantheon. An Indian mathematician of genius, but lacking in formal instruction, he

was discovered by G. H. Hardy, to whom he had mailed page after p age covered with formulas

each more incredible than the last. The reader may read Ramanujan, an Indian Mathematician

by Hardy, in the book [46]. One will also ﬁnd there the famous anecdote of the number

“1729.”

In relativistic quantum mechanics, one cannot have a description of matter which is purely

electronic, for instance; positrons necessarily occur, as was discovered by Dirac [49].

Solutions of exercises 129

with ω

(2l + 1 )π

and E

def

= (m

+ p

)

1/2

1. Put this sum in the form of a sum of residues of a well-chosen function f (z). Make a

drawing of the complex plane with the corresponding poles.

2. Does the chosen function admit any other poles?

3. By c o nsidering the decay of the function f (z) at inﬁnity, show that the sum of the

residues vanishes.

4. Show then that we have

N ( p) = −tanh



βE

−βµ



+ tanh



βE

+ βµ



= 2N

( p) −2N

pos

( p),

where we use the electronic and positronic Fermi distributions

( p) =

β(E

−µ)

+ 1

and N

pos

( p) =

β(E

+µ)

+ 1

Interpret these t wo terms.

SOLUTIONS

 Solution of exercise 4 .1 on page 90. Put f = P + i Q.

We start by remarking that property (ii) implies all the others. Let us show the equivalence

of (ii) and (iii). Suppose, for example, that P = C

. Then, at any point,

∂ P

∂ x

∂ P

∂ y

= 0,

which, by the Cauchy equations, implies that

∂ Q

∂ y

∂ Q

∂ x

= 0

and hence that Q = C

. One deduces that (ii) and (iii) are equivalent. Moreover, (ii) and (iii),

together, imply property (i). Thus we have shown the equivalence of (i), (ii), and (iii).

Let us show that (iv) implies (iii ) — this will prove al so that (iv) implies (i) and (ii). Assume

then property (iv). We can also assume that f is not the zero fu nction (which is an obvious

case). Then f has no zero at all, and so the sum P

+ Q

= C

is never zero. We have

0 =

∂ |f |

∂ x

= 2P

∂ P

∂ x

+ 2Q

∂ Q

∂ x

Cauchy

= 2P

∂ Q

∂ y

+ 2Q

∂ Q

∂ x

and

0 =

∂ |f |

∂ y

= 2P

∂ P

∂ y

+ 2Q

∂ Q

∂ y

= −2P

∂ Q

∂ x

+ 2Q

∂ Q

∂ y

The two preceeding equations can therefore be written in the form



Q P

−P Q



∂ Q/∂ x

∂ Q/∂ y



= 0.

But the determinant of this matrix is P

+ Q

which is everywhere non-zero. So we deduce

that, at any point, we have

∂ Q

∂ x

∂ Q

∂ y

= 0 and, consequently, that Q = C

130 Complex Analysis I

There only remains to show that (v) implies (ii). Assume that both f and f are holomorphic;

then the Cauchy equations allow us to write

( f ∈ H ) =⇒

∂ P

∂ x

∂ Q

∂ y

and ( f ∈ H ) =⇒

∂ P

∂ x

∂(−Q)

∂ y

and hence ∂ P /∂ x = 0; similarly ∂ P /∂ y = 0, so that P = C

. Which, taking into account

the remarks above, completes the proof.

 Solution of exercise 4 .4. One checks ﬁrst that the l ap l acian can be written △ = 4∂∂. Then

write △|f |

= 4∂ ∂( f f ) = 4 ∂



(∂ f ) f + f (∂ f )



. Since f is holomorphic, we have ∂ f = 0

hence △|f |

= 4∂



f ∂ f



= 4∂ f ·∂ f since ∂ f is an antiholo morphic function; th u s ∂∂ f = 0.

To conclude, one ﬁnds

△|f |

= 4∂ f ·∂ f = 4 |∂ f |

 Solution of exercise 4 .6. Disregarding the trivial case where f = 0, write then f = f

/ f

at any point where f does not vanish. But since f

is holomorphic, its zeros are isolated, and

therefore those of f also, since they are the same. Denote by Z the set of these zeros. Then

f is holomorphic on Ω \ Z and bounded in the neighborhood of each point in Z, which are

therefore artiﬁcial singularities. Hence, if we extend by continuity the functi on g = f

/ f

(by

putting g(z) = 0 for any x ∈ Z), the resulting function g is holo morphic by Theorem 4.56 on

page 108, and moreover g = f by construction.

 Solution of exercise 4 .8. The function z 7→ (1/z

) being holomorphic o n the open set

Ω =



z ∈ C ; Im(z) > Re(z)



which contains the contour T , it admits a p rimitive on Ω ,

which is evidently z 7→ −1/z. Then

dz =



−



 Solution of exercise 4 .9. Show that the integrals on the vertical segments tend to 0 when

[R → ∞]. Show moreover that

−R

−(x+ia/2)

dx = e

−R

−x

cos ax dx

by parity. The integral considered is equal to

πe

−a

 Solution of exercise 4 .10. The Laurent series expansion of the sine function coincides with

its Taylor series expansion and is given by

sin z = z −

−··· ; hence

sin z

−

−··· ,

and the residue is the coefﬁcient of 1/z, namely 1.

 Solution of exercise 4 .11. For the ﬁrst integral, put

f (z) =

(1 + z) e

2i z

+ 2z + 2

and integrate by closing the contour from above (with justiﬁcation!). The only residue inside

the contour is the one in z = 1 + i. The desired integral is the imaginary part of

f (z) dz =

iπe

−2−2i

, which is (π cos2)/e

For the second i ntegral, close the contour from above, using Jordan’s second lemma, with

f (z) =

(1 + z

)

(z −i)

(z + i)

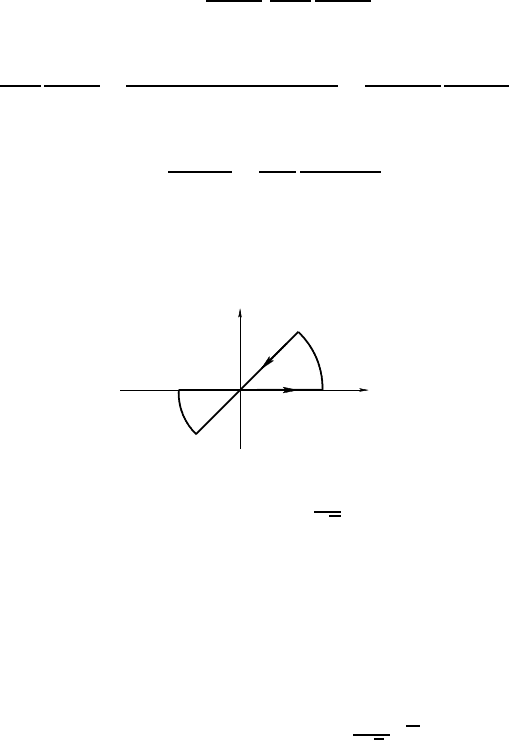
Solutions of exercises 131

Then the desired integral i s equal to 2iπ Res ( f ; i) (or, if the contour is closed from below, to

−2iπ Res ( f ; −i)). But, according to formula (4.10), page 116, since i is a po le of order n,

Res ( f ; i) =

(n −1)!

n−1

(z + i)



z=i

An easy induction shows that

n−1

(z + i)

(−n) ·(−n −1) ···(−2n + 2)

(z + i)

2n−1

(−1)

n−1

(z + i)

2n−1

(2n −2)!

(n −1)!

which leads, after short algebraic manipulations, to

+∞

−∞

(1 + z

)

2n−2

(2n −2)!



(n −1)!



 Solution of exercise 4 .12. The Fresnel integral is not deﬁned in the Lebesgue sense since

the modulus of e

i x

is constant and nonzero, and therefore not integrable. However, the

integral is deﬁned as an “improper integral,” which means that the integral I (R, R

′

) admits a

limit as R and R

′

(separately) tend to inﬁnity. Consider now the contour

C (R, R

′

)

def

−R

′

The integral on the upper eight h arc γ

′

is, by a change of variable, equal to

′

i z

dz =

′

iζ

dζ

where C

′

is the upper quarter-ci rcle with radius R

′2

, and this last integral does tend to 0 by

Jordan’s second lemma. The second eighth of the circle is treated in the same manner. Since

the integral on C (R, R

′

) vanishes (the function is holomorphic), the Fresnel integral is equal

to an integral on the line segment with angle π/4:

lim

R,R

′

→+∞



′

−R

i x

dx −

′

−R

i(e

iπ/4



= 0,

hence

+∞

−∞

i x

dx = e

iπ/4

+∞

−∞

−x

dx =

1 + i

π.

 Solution of exercise 4 .13. Denote by F (ν) the integral under consideration. It c an be put

in the form

F (ν) = e

−πν

−π(x+iν)

dx.

Denote by γ

the line wi th imaginary part ν, hence parallel to the real axis. Then, using

Cauchy’s theorem for the function z 7→ e

−πz

, which is holomorphic on C, show as in

exercise 4.9, that

−πz

dz =

+∞

−∞

−πx

dx = 1,

which gives F ( ν) = e

−πν

132 Complex Analysis I

 Solution of exercise 4 .16. Consider the contour γ(R) made from the line segments [0, R],



0, R e

iπ/3



and the part of the circle C (0; R) with argument varying from 0 and π/3 . Let

g be the function g : z 7→ z

+ 1. Then the function f = 1/g has only one pole inside this

contour, at the point ζ = e xp(iπ/6). Check then (using the ﬁrst Jordan lemma and a few

algberaic computations) that

γ(R)

f (z) dz −−−→

R→+∞



1 −e

iπ/3



+∞

+ 1

Using the residue theorem, it follows therefore that

+∞

+ 1

2iπ Res ( f ; ζ )

1 −e

iπ/3

To compute the preceeding residue, one may notice that

Res ( f ; ζ ) = lim

z→ζ

z −ζ

g(z)

= lim

z→ζ

z −ζ

g(z) − g(ζ )

because g(ζ ) = ζ

−1 = 0

′

(ζ )

−5π/6

Thus we get

+∞

+ 1

iπ

−5π/6

1 −e

iπ/3

 Solution of exercise 4 .17. De ﬁne

f (z) =

log z

1 + z

where the logarithm function is deﬁned on C \ R

−

, for instance. Integrate on the contour

going from ǫ to R (for ǫ > 0), followed by an arc with angle 2π/3, then by a line segment

toward the o rigin, but ﬁnished by another arc of the circle with radius ǫ. Show that the

integrals on the circles tend to 0 when R tends to inﬁnity and ǫ to 0. The only residue inside

the contour is from the pole at z = e

iπ/3

and is equal to −

−iπ/6

. Compute the integral on

the second side in terms of the desired integral and in terms of

+∞

1 + x

dx =

2π

(which can be computed using the partial f ractio n expansion of 1/(1 + x

), for instance).

One ﬁnds then

+∞

log x

1 + x

dx = −

 Solution of exercise 4 .18. Show that the function is integrable using a Taylor expansion at

1 and −1. Integrate on a contour which consists of the li ne segment from −R to R, avoiding

the poles at 1 and −1 by half-circles above the real axis with small radius ǫ, and close the

contour by a half-c ircle of radius R. Show that the integral on the large circle of

f (z) =

iπz/2

−1

tends to 0 and compute the integrals on the small circles (which do not vanish; the ir sum is

equal to π in the limit where [ǫ → 0 ]).

Hence one ﬁnds that

+∞

−∞

f (x) dx = π and the desired integral has value −π/2.

Solutions of exercises 133

 Solution of exercise 4 .24. Notice that

T + ia

S =

∞

n=1

−ia

)

Use then the result given by equation (4.15), page 123, and take the real and imaginary parts,

respectively.

 Solution of exercise 4 .25. Let

f (z) = π

cotan(πz) coth(πz)

This function has poles at n and in, for any n ∈ Z. The residue at n 6= 0 is simply coth(πn)/n

and the residue at in 6= 0 is cotan(iπn)/(in)

= coth(πn)/n

, which gives us that the integ ral

of f on the square with center at 0 and edges parallel to the axis at distance R = (n +

)π

(which does not p ass through any pole) is

= 2iπ

k=n

k=−n

k6=0

2 coth πk

+ 2iπ Res ( f ; 0).

Since (by an adaptation to this situation of Jordan’s second le mma) I

tends to 0 when n tends

to inﬁnity, we deduce that

S =

k=1

coth πk

= −

Res ( f ; 0).

It sufﬁces now to e xpand π coth πz cotan πz to order 6 around 0 (by hand for the most

courageous, with a computer for the others):

π coth πz cotan πz =

πz

−

7π

−

19π

14 175

+ O(z

)

which indicates that the residue of f at 0 is −19π

/14 175, and the formula stated follows.

134 Complex Analysis I

Sidebar 3 (Differentiability of a function on RR

) Consider

f : R

−→ R

(x, y) 7−→ f (x, y),

a function of two real variables with values in R

. Denote its coordinates by f = ( f

, f

);

thus the functions f

and f

take values in R.

The function f is differentiable at a point (x

, y

) ∈ R

if there e xists a linear map

Θ ∈ L (R

) w hich satisﬁes

f (x

+ h, y

+ k) = f (x

, y

) + Θ(h, k) + o(h, k) [(h, k) → (0, 0)].

Such a linear map Θ is called the differential of f at the point ( x

, y

), and is

denoted d f

, y

)

. It can be represented as a 2 ×2 matrix:

mat



d f

, y

)









∂ f

∂ x

∂ f

∂y

∂ f

∂ x

∂ f

∂y







which means that

+ h, y

+ k)

+ h, y

+ k)

, y

)

, y

)







∂ f

∂ x

∂ f

∂y

∂ f

∂ x

∂ f

∂y







+ o(h,k)

, y

)

, y

)







∂ f

∂ x

·h +

∂ f

∂y

·k

∂ f

∂ x

·h +

∂ f

∂y

·k







+ o(h, k).

The map which associates d f

, y

)

to (x

, y

) is called the differential of f and is d e-

noted d f .

It is customary to write dx : (h, k) 7→ h and dy : (h, k ) 7→ k, and consequently the

differential d f can also be written, in the complex notation f = f

+ i f

, as

d f =

∂ f

∂ x

dx +

∂ f

∂ y

dy. (∗)

(Notice that we began with a vector function ( f

, f

) and ended with a scalar fu nction

+ i f

; therefore the matrix of d f is a simple line 1 ×2 and no more a 2 × 2 square

matrix. It is now the matr ix of a linear form.)

If f is differentiable, then its partial derivatives are well-deﬁned. The converse is not true,

but still, it the partial derivatives of f are deﬁned and continuous on an open set Ω ⊂ R

then f is indeed differentiable, and its differential d f satisﬁes the equation (∗).

Chapter

Complex Analysis II

5.1

Complex logarithm; multivalued functions

5.1.a The complex logarithms

We seek to extend the real logarithm function x 7→ log x, deﬁned on R

+∗

, to

the complex plane — or at least to a part, as large as possible, of the complex

plane.

The most natural idea is to come back to one of the possible deﬁnitions

of the real logarithm: it is the primitive of x 7→ 1/x which vanishes at x = 1.

Let us therefore try to “primitivize” the function z 7→ 1/z and so put, for any

z ∈ C

∗

L (z)

def

γ(z)

dζ , (5.1)

where γ(z) is a path in the complex plane joining 1 to z, not going through 0

(so that the integral exists). Does equation (5.1) really deﬁne a function? The

answer is “yes” if any choice of the path γ leads to the same value of L(z),

and “no” otherwise. However, two paths γ

and γ

, joining 1 to z, but going

on “opposite sides” of the point 0, give different results (see Figure 5.1); if we

call γ the path consisting of γ

followed by −γ

, the integral of 1/ζ around γ

is equal to 2πi times the residue at 0 (which is 1), times the number of turns

of γ around 0; so, in the end,

(1/ξ) dξ = 2πi.

136 Complex Analysis II

Fig. 5.1 — It is not possible to integrate the function z 7→ 1/z on the complex plane, since

the result depends on the chosen path. Thus, the integrals on the solid contour

and the dashed c o ntour γ

differ by 2πi.

Consequently, it is not possible to d eﬁne the complex logarithm on the

punctured plane C

∗

= C \{0}.

Still, we may restrict our ambitions a bit and only consider the plane from

which a half-line has been removed, namely C \R

−

PROPOSITION 5.1 The complex plane minus the half-line of negative real numbers

C \R

−

is simply connected.

A consequence of this theorem is that, on t his simply connected set, all

closed paths are homotopic

to a point, and the relation (5.1) does deﬁne a

function correctly.

DEFINITION 5.2 The function L(z) deﬁned by

L (z)

def

γ(z)

dζ , (5.2)

where γ(z) is a path inside C \ R

−

joining 1 to z, is called the principal

complex logarithm.

Notice that one could just as well remove another half-line from the com-

plex plane, for instance, the half-line of positive real numbers, or one of the

half-lines of the purely imaginary axis. Even more, it would be possible to take

an arbitrary simple curve C joining 0 to inﬁnity; then, on the complement

C \C , which is simply connected, one can deﬁne a new logarithm function.

DEFINITION 5.3 A cut is any simple curve joining 0 to inﬁnity in the com-

plex plane. To each cut C is as sociated a logarithm function ℓ

on C \C .

The point 0 is called a branch point.

The various logarithm functions are of course related to each other by the

following result:

I.e., a closed path can be contracted continuously to a point, see p age 575.